6.2: Вирішення нелінійних рівнянь

Ми починаємо з введення властивості, яка буде широко використовуватися в цьому і майбутніх розділах.

Нерухомість продукту

Якщо добуток двох і більше чисел дорівнює нулю, то хоча б одне з чисел має дорівнювати нулю. Тобто, якщо

$ab =0$

потім

$a = 0$або$b =0$

Давайте використаємо властивість нульового добутку для вирішення декількох рівнянь.

Приклад$\PageIndex{1}$

Вирішити для$x$:$(x+3)(x-5)=0$

Рішення

Добуток двох множників дорівнює нулю.

$$(x+3)(x-5)=0 \nonumber$$

Значить, хоча б один з факторів повинен дорівнювати нулю. Використовуючи властивість нульового добутку, задайте кожен коефіцієнт рівним нулю, потім вирішуйте отримані рівняння для$x$.

$$\begin{aligned} x+3 &=0 \\ x &=-3 \end{aligned} \nonumber$$

або

$$\begin{aligned} x-5 &=0 \\ x &=5 \end{aligned} \nonumber$$

Отже, рішення є$x = −3$ і$x =5$

Перевірка:

Переконайтеся, що кожне рішення відповідає вихідному рівнянню.

Замінник$−3$ для$x$:

$$\begin{aligned}(x+3)(x-5) &=0 \\(-3+3)(-3-5) &=0 \\(0)(-8) &=0 \\ 0 &=0 \end{aligned} \nonumber$$

Замінник$5$ для$x$:

$$\begin{aligned}(x+3)(x-5) &=0 \\(5+3)(5-5) &=0 \\(8)(0) &=0 \\ 0 &=0 \end{aligned} \nonumber$$

Тому що кожна перевірка виробляє істинне твердження, обидва$x = −3$ і$x = 5$ є рішеннями$(x + 3)(x−5) = 0$.

Вправа$\PageIndex{1}$

Вирішити для х:$(x-7)(x-2)=0$

Відповідь

$7$,$2$

Властивість нульового продукту також працює однаково добре, якщо присутні більше двох факторів. Наприклад, якщо$abc = 0$, то або$a = 0$ або$b = 0$ або$c = 0$. Давайте використаємо цю ідею в наступному прикладі.

Приклад$\PageIndex{2}$

Вирішити для$x$:$x(2x + 9)(3x−5) = 0$

Рішення

Добуток трьох множників дорівнює нулю.

$$x(2x + 9)(3x−5) = 0 \nonumber$$

Використовуючи властивість нульового добутку, задайте кожен коефіцієнт рівним нулю, потім вирішуйте отримані рівняння для$x$.

$$x=0 \nonumber$$

або

$$\begin{align*} 2x + 9 &= 0\\ 2x &= -9\\ x &= -\dfrac{9}{2} \end{align*} \nonumber$$

або

$$\begin{align*} 3x - 5 &= 0\\ 3x &= 5\\ x &= \dfrac{5}{3} \end{align*} \nonumber$$

Отже, рішення є$x = 0$$x = −9/2$, і$x =5 /3$. Ми закликаємо читача перевірити рішення.

Вправа$\PageIndex{2}$

Вирішити для$x$:$6x(x + 4)(5x + 1) = 0$

Відповідь

$0$,$−4$,$−1/5$

Лінійний проти нелінійних

Всі рівняння, розв'язані в попередніх розділах, були прикладами того, що називаються лінійними рівняннями. Якщо найвища потужність змінної, для якої ми вирішуємо, одна, то графи, що беруть участь, - це лінії. Звідси і термін, лінійне рівняння. Однак якщо потужність змінної, яку ми вирішуємо, перевищує одиницю, то графи, що беруть участь, є кривими. Звідси і термін, нелінійне рівняння. У цьому розділі ми дізнаємося, як розв'язувати нелінійні рівняння за участю поліномів. Однак спочатку переконаємось, що ми можемо розпізнати різницю між лінійним та нелінійним рівнянням.

Визначення: лінійні та нелінійні рівняння

Використовуйте наступні умови, щоб визначити, чи рівняння є лінійним або нелінійним.

1. Якщо найвища потужність змінної, для якої ми розв'язуємо, одна, то рівняння лінійне.
2. Якщо найвища потужність змінної, для якої ми розв'язуємо, більше одиниці, то рівняння нелінійне.

Приклад$\PageIndex{3}$

Якщо інструкція «вирішувати для»$x$, класифікуйте кожне з наступних рівнянь як лінійне або нелінійне.

1. $3x−5=4−7x$
2. $x^2 =8x$

Рішення

Оскільки інструкція «вирішувати для»$x$, щоб визначити, чи є рівняння лінійним чи нелінійним, ми визначаємо найбільшу потужність$x$ присутніх у рівнянні.

1. Найвища потужність$x$ присутніх в рівнянні$3x− 5=4− 7x$ - одна. Значить, це рівняння є лінійним.
2. Рівняння$x^2 =8 x$ містить ступінь$x$ вище одиниці (воно містить$x^2$). Значить, це рівняння нелінійне.

Вправа$\PageIndex{3}$

Класифікують наступне рівняння як лінійне або нелінійне:$2x = x^3 −4$

Відповідь

нелінійних

Тепер, коли ми можемо класифікувати рівняння як лінійні або нелінійні, давайте представимо стратегії розв'язання кожного типу, перший з яких вже повинен бути знайомим.

Стратегія розв'язання лінійного рівняння

Якщо рівняння лінійне, розпочніть процес розв'язання, перемістивши всі члени, що містять змінну, яку ви вирішуєте, на одну сторону рівняння, а потім перемістіть всі члени, які не містять змінної, яку ви вирішуєте, на іншу сторону рівняння.

Приклад$\PageIndex{4}$

Вирішити для$x$:$3 x−5=4−7x$

Рішення

Оскільки інструкція «вирішувати для$x$», і ми зауважимо, що найбільша сила$x$ теперішнього - одна,$3x−5=4−7x$ рівняння лінійне. Отже, стратегія полягає в тому, щоб перемістити всі члени, що містять$x$ в одну сторону рівняння, а потім перемістити всі інші члени на іншу сторону рівняння.

$$\begin{array}{rlrl}{3 x-5} & {=4-7 x} & {\color {Red} \text { Original equation. }} \\ {3 x-5+7 x} & {=4} & {\color {Red} \text { Add } 7 x \text { to both sides. }} \\ {3 x+7 x} & {=4+5} & {\color {Red} \text { Add } 5 \text { to both sides. }}\end{array} \nonumber$$

Зверніть увагу, як нам вдалося перенести всі члени, що містять$x$ в одну сторону рівняння, і всі члени, які не містять$x$, на іншу сторону рівняння.

$$\begin{array}{rlrl}{10 x} & {=9} & {} & {\color {Red} \text { Simplify both sides. }} \\ {x} & {=\dfrac{9}{10}} & {} & {\color {Red} \text { Divide both sides by } 10 .}\end{array} \nonumber$$

Отже, рішення$3x−5=4−7x$ є$x =9 /10$. Читачам рекомендується перевірити це рішення.

Вправа$\PageIndex{4}$

Додайте сюди текст вправ.

Відповідь

$1/4$

Ситуація значно відрізняється, коли рівняння нелінійне.

Стратегія розв'язання нелінійного рівняння

Якщо рівняння нелінійне, спочатку перемістіть все в одну сторону рівняння, зробивши одну сторону рівняння рівнянням рівною нулю. Продовжуйте процес вирішення шляхом факторингу та застосування властивості нульового продукту.

Приклад$\PageIndex{5}$

Вирішити для$x$:$x^2 = 8x$

Рішення

Оскільки інструкція «вирішувати для»$x$, а найвища потужність$x$ більша за одиницю, рівняння$x^2 =8x$ нелінійне. Отже, стратегія вимагає, щоб ми перемістили всі члени в одну сторону рівняння, зробивши одну сторону нулем.

$$\begin{array}{rlrl}{x^{2}} & {=8 x} \quad {\color {Red} \text { Original equation. }} \\ {x^{2}-8 x} & {=0} \quad {\color {Red} \text { Subtract } 8 x \text { from both sides. }}\end{array} \nonumber$$

Зверніть увагу, як нам вдалося перенести всі члени в одну сторону рівняння, зробивши одну сторону рівною нулю. Щоб закінчити рішення, ми враховуємо$\mathrm{GCF}$ на лівій стороні.

$$x(x-8) = 0 \quad \color {Red} \text {Factor out the GCF.} \nonumber$$

Зверніть увагу, що тепер у нас є добуток двох факторів, що дорівнює нулю. За властивістю нульового добутку, або перший коефіцієнт дорівнює нулю, або другий коефіцієнт дорівнює нулю.

$$\begin{array}{r}{x=0 \quad \text { or } \quad x-8=0} \\ {x=8}\end{array} \nonumber$$

Значить, рішення є$x = 0$ і$x = 8$.

Перевірка:

Переконайтеся, що кожне рішення відповідає вихідному рівнянню.

$$\begin{array}{l}{\text { Substitute } 0 \text { for } x :} \\ {\qquad \begin{aligned} x^{2} &=8 x \\(0)^{2} &=8(0) \\ 0 &=0 \end{aligned}}\end{array} \nonumber$$

$$\begin{array}{l}{\text { Subtitute } 8 \text { for } x :} \\ {\qquad \begin{aligned} x^{2} &=8 x \\(8)^{2} &=8(8) \\ 64 &=64 \end{aligned}}\end{array} \nonumber$$

Зверніть увагу, що обидва результати є справжніми твердженнями, гарантуючи, що обидва$x = 0$ і$x = 8$ є рішеннями$x^2 =8x$

Вправа$\PageIndex{5}$

Вирішити для$x$:$x^2 =−5x$

Відповідь

$0$,$-5$

Попередження!

Наступне невірно!

Розглянемо, що станеться, якщо ми розділимо обидві сторони рівняння$x^2 =8x$ в прикладі$\PageIndex{5}$ на$x$:

$$\begin{aligned} x^{2} &=8 x \\ \dfrac{x^{2}}{x} &=\dfrac{8 x}{x} \\ x &=8 \end{aligned} \nonumber$$

Зверніть увагу, що ми втратили другу відповідь, знайдену в Приклад$\PageIndex{5}$,$x = 0$. Цей приклад демонструє, що ви ніколи не повинні ділити на змінну, для якої ви вирішуєте! Якщо ви це зробите, і скасування відбудеться, ви втратите відповіді.

Спробуємо розв'язати нелінійне рівняння, яке вимагає факторингу шляхом групування.

Приклад$\PageIndex{6}$

Вирішити для$x$:$6x^2 +9x−8x−12 = 0$

Рішення

Оскільки ми розв'язуємо для$x$ і є сила$x$ більша за одиницю, це рівняння є нелінійним. Отже, першим кроком є переміщення всього в одну сторону рівняння, зробивши одну сторону рівною нулю. Ну, що вже зроблено, так що давайте фактор лівої сторони шляхом групування. Зауважте, що ми можемо перерахувати з перших двох термінів і$−4$ з двох других.$3x$

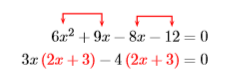
Фактор з загального фактора$2x + 3$.

$$(3x-4){\color {Red}(2x + 3)}=0 \nonumber$$

Тепер у нас є добуток двох факторів, що дорівнює нулю. Використовуйте властивість нульового продукту, щоб записати:

$$\begin{aligned} 3x-4 &=0 \\ 3x &= 4 \\ x &=\dfrac{4}{3} \end{aligned} \nonumber$$

або

$$\begin{aligned} 2x+3 &=0 \\ 2x &= -3 \\ x &= -\dfrac{3}{2} \end{aligned}$$

Значить, рішення є$x =4 /3$ і$x =−3/2$.

Перевірка:

Давайте скористаємося графічним калькулятором, щоб перевірити рішення$x =4 /3$. Спочатку збережіть рішення$4/3$ у змінній$\mathbb{X}$ за допомогою наступних натискань клавіш (див. Перше зображення на рис$\PageIndex{1}$.

Рисунок$\PageIndex{1}$ вказує на те, що вираз$6x^2 +9x−8x−12$ дорівнює нулю, коли$x =4 /3$.

Малюнок$\PageIndex{1}$: Перевірка розчину$x =4 /3$.

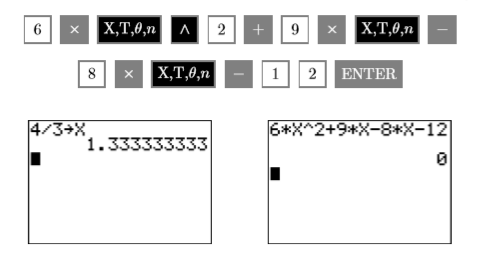
Тому розчин$x =4 /3$ перевіряє. Читачам рекомендується використовувати свої графічні калькулятори для перевірки другого рішення$x = −3/2$.

Вправа$\PageIndex{6}$

Вирішити для$x$:$5x^2 −20x−4x + 16 = 0$

Відповідь

$4/5$,$4$

Використання графічного калькулятора

У цьому розділі ми будемо використовувати дві різні процедури калькулятора, щоб знайти рішення нелінійного рівняння. Перш ніж підібрати калькулятор, давайте спочатку використаємо алгебраїчний метод для вирішення рівняння$x^2 = −5x$. Рівняння нелінійне, тому першим кроком є переміщення всього в одну сторону рівняння, зробивши одну сторону рівною нулю.

$$\begin{aligned} x^{2} &= -5x \quad \color {Red} \text { Nonlinear. Make one side zero. } \\ x^{2}+5 x &= 0 \quad \color {Red} \text { Add } 5x \text { to both sides. } \\ x(x+5) &= 0 \quad \color {Red} \text { Factor out the GCF. } \end{aligned} \nonumber$$

Використовуйте властивість нульового добутку, задаючи кожен коефіцієнт рівним нулю, потім вирішуючи отримані рівняння для$x$.

$$x=0 \nonumber$$

або

$$\begin{aligned} x+5&=0 \\ x&=-5 \end{aligned} \nonumber$$

Значить, рішення є$x = 0$ і$x = −5$.

Тепер ми скористаємося калькулятором, щоб знайти рішення$x^2 = −5x$. Перша методика використовує процедуру 5: перетину в меню калькулятора.

Приклад$\PageIndex{7}$

Використовуйте утиліта 5:intersect на графічному калькуляторі, щоб вирішити рівняння$x^2 = −5x$ для$x$.

Рішення

Завантажте ліву частину входу$x^2 = −5x$$\mathbb{Y1}$ та праву частину$\mathbb{Y2}$ (див. Рис.$\PageIndex{2}$). Вибір 6:ZStandard з меню ZOOM створює графіки, показані на зображенні праворуч на малюнку$\PageIndex{2}$.

Малюнок$\PageIndex{2}$: Намалюйте графіки кожної сторони рівняння$x^2 = −5x$.

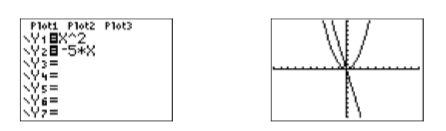
Зверніть увагу, що граф$y = x^2$ - це парабола, яка відкривається вгору, з вершиною (точкою повороту) біля початку. Цей графік показує, чому рівняння$x^2 = −5x$ називається нелінійним рівнянням (не всі задіяні графіки є лініями). Далі на графіку$y = −5x$ йде лінія з нахилом$−5$ і$y$ -перехопленням у початку.

Два графіки, очевидно, перетинаються біля початку, але також здається, що може бути ще одна точка перетину, яка є oекраном. Давайте$\mathbb{Ymax}$ збільшимо спробу виявити другу точку перетину. Після деяких експериментів параметри, показані на першому зображенні на малюнку,$\PageIndex{3}$ виявляють обидві точки перетину. Натискання кнопки GRAPH створює зображення праворуч на малюнку$\PageIndex{3}$.

Малюнок$\PageIndex{3}$: Налаштуйте параметри WINDOW, щоб виявити обидві точки перетину.

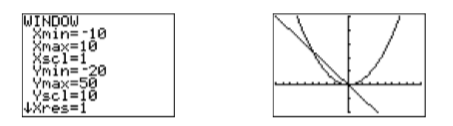
Щоб знайти розв'язки рівняння$x^2 =−5x$, ми повинні знайти координати точок, де графи$y = x^2$ і$y = −5x$ перетинаються. $x$-координата кожної точки перетину буде розв'язком рівняння$x^2 = −5x$.

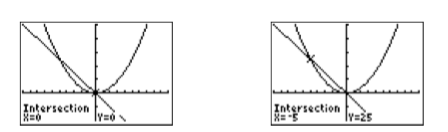
• Почніть з вибору 5: перетин у меню CALC. Коли з'явиться запит на «Перша крива?» , натисніть клавішу ENTER. Коли буде запропоновано «Друга крива?» , натисніть клавішу ENTER. Коли з'явиться запит на «Вгадати», натисніть клавішу ENTER. Результатом є точка,$(0,0)$ показана на зображенні зліва на малюнку$\PageIndex{4}$.
• Повторіть процес вдруге. Виберіть 5: перетин в меню CALC. Коли з'явиться запит на «Перша крива?» , натисніть клавішу ENTER. Коли буде запропоновано «Друга крива?» , натисніть клавішу ENTER. Коли з'явиться запит на «Вгадати», скористайтеся клавішею зі стрілкою вліво, щоб перемістити курсор ближче до крайньої лівої точки перетину, а потім натисніть клавішу ENTER. Результатом є точка,$(−5,25)$ показана на зображенні праворуч на малюнку$\PageIndex{4}$.

Малюнок$\PageIndex{4}$: Використовуйте утиліту 5:intersect, щоб знайти точки перетину.

Повідомлення про рішення по домашньому завданню:

Дублюйте зображення у вікні перегляду калькулятора на сторінці домашнього завдання. Використовуйте лінійку, щоб намалювати всі лінії, але від руки будь-які криві.

Малюнок$\PageIndex{5}$: Повідомлення про графічне рішення на домашнє завдання.

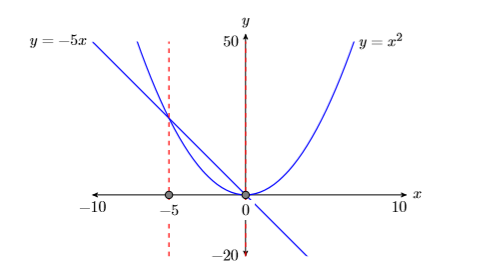
• Позначте горизонтальну і вертикальну$x$ осі і$y$ відповідно (див. Рис.$\PageIndex{5}$).
• Розмістіть параметри WINDOW в кінці кожної осі (див. Рис.$\PageIndex{5}$).
• Позначте кожен граф своїм рівнянням (див. Малюнок$\PageIndex{5}$).
• Пропустіть пунктирні вертикальні лінії через кожну точку перетину. Затіньте та позначте$x$ -значення точок, де пунктирна вертикальна лінія перетинає$x$ вісь -. Це розв'язки рівняння$x^2 =−5x$ (див. Малюнок$\PageIndex{5}$).

Значить, рішення$x^2 = −5x$ є$x = −5$ і$x = 0$. Зауважте, що тепер вони відповідають розв'язкам, знайденим за допомогою алгебраїчної техніки.

Вправа$\PageIndex{7}$

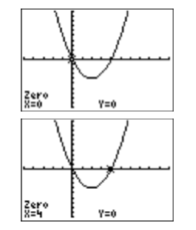
Використовуйте утиліта 5:intersect на графічному калькуляторі, щоб вирішити рівняння$x^2 =4x$ для$x$.

Відповідь

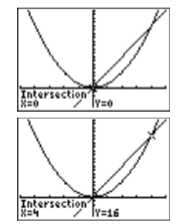
Перш ніж продемонструвати другий метод графічного калькулятора для розв'язання нелінійних рівнянь, давайте згадаємо визначення нуля функції, яке вперше було представлено в розділі 3 глави 5.

Нулі і$x$-intercepts

Точки, де графік$f$ перетинає$x$ -вісь, називаються$x$ -перехопленнями графіка$f$. $x$-value кожного$x$ -intercept називається нулем функції$f$.

Тепер ми будемо використовувати 2: нульову утиліту з меню CALC, щоб знайти рішення рівняння$x^2 = −5x$.

Приклад$\PageIndex{8}$

Використовуйте 2: нуль утиліту на графічному калькуляторі, щоб вирішити рівняння$x^2 = −5x$ для$x$.

Рішення

Спочатку зробіть одну сторону рівняння рівною нулю.

$$\begin{aligned}x^{2} &=-5 x \quad \color {Red} \text { Make one side zero. } \\ x^{2}+5 x &=0 \quad \color {Red} \text { Add } 5 x \text { to both sides. }\end{aligned} \nonumber$$

Щоб визначити значення цієї марки$x$$x^2 +5x = 0$, ми повинні знайти точки, де графік$f(x)=x^2 +5x$ перетинає$x$ вісь -. Ці точки є$x$ -перехопленнями графіка$f$ і$x$ -значення цих точок є нулями функції$f$.

Завантажте функцію$f(x)=x^2 +5 x$$\mathbb{Y1}$, а потім виберіть 6:ZStandard, щоб створити зображення на малюнку$\PageIndex{6}$. Зверніть увагу, що графік$f$ має два$x$ -перехоплення, а$x$ -значення кожної з цих точок є нулями функції$f$.

Малюнок$\PageIndex{6}$: Намалюйте графік$p(x)=x^2 +5x$.

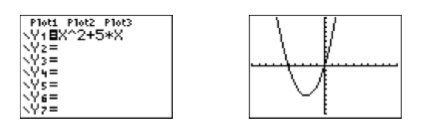
Примітка

Часто легше знайти розв'язки нелінійного рівняння, зробивши одну сторону нулем і визначаючи, де графік результуючої функції перетинає$x$ вісь -.

Виберіть 2:нуль в меню CALC (див. Рис.\(\PageIndex{7}\)).

Малюнок$\PageIndex{7}$: Встановлення лівої та правої меж при використанні 2: нульової утиліти для$x$ пошуку -перехоплень графіка$f(x)=x^2 +5x$.

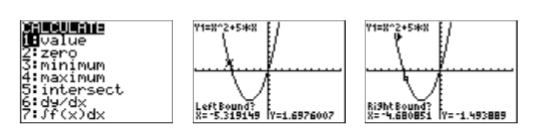
• Калькулятор відповідає, запитуючи «Ліва межа?» За допомогою клавіші зі стрілкою вліво перемістіть курсор так, щоб він лежав зліва від$x$ -перехоплення поблизу$(−5,0)$ (див. Друге зображення на малюнку$\PageIndex{7}$), потім натисніть клавішу ENTER.
• Калькулятор відповідає, запитуючи «Right Bound?» Перемістіть курсор так, щоб був трохи праворуч від x-перехоплення поблизу$(−5,0)$ (див. Третій малюнок$\PageIndex{7}$), після чого натисніть клавішу ENTER.
• Калькулятор відповідає, запитуючи «Вгадай?» Зверніть увагу на дві трикутні позначки у верхній частині вікна перегляду на першому зображенні на малюнку$\PageIndex{8}$, які позначають ліву та праву межі. Поки ви розміщуєте курсор так, щоб значення x розташування курсора лежало між цими двома мітками, ви зробили правильне припущення. Оскільки курсор вже лежить між цими двома позначками, ми зазвичай залишаємо його там, де він є, і натискаємо клавішу ENTER.

Малюнок$\PageIndex{8}$: Встановлення правої межі та припущення.

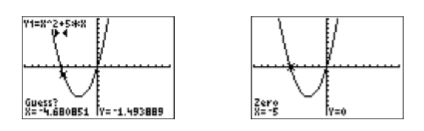
Зробивши здогадку та натиснувши клавішу ENTER, калькулятор переходить до наближення$x$ -перехоплення, яке лежить між раніше позначеною лівою та правою межею (див. Друге зображення на рис$\PageIndex{8}$. Отже, це$x$ -перехоплення є$(−5,0)$, роблячи$−5$ нуль$f(x)=x^2 +5x$ і рішення рівняння$x^2 +5x = 0$.

Ми залишимо це нашим читачам повторити процес 2: нуль, щоб знайти другий нуль у початку.

Повідомлення про рішення по домашньому завданню:

Дублюйте зображення у вікні перегляду калькулятора на сторінці домашнього завдання. Використовуйте лінійку, щоб намалювати всі лінії, але від руки будь-які криві.

• Позначте горизонтальну і вертикальну$x$ осі і$y$ відповідно (див. Рис.$\PageIndex{9}$).
• Розмістіть параметри WINDOW в кінці кожної осі (див. Рисунок$\PageIndex{9}$).
• Позначте кожен граф своїм рівнянням (див. Малюнок$\PageIndex{9}$).
• Пропустіть пунктирні вертикальні лінії через кожну$x$ -перехоплення. Затіньте та позначте$x$ -значення кожного$x$ -перехоплення. Це розв'язки рівняння$x^2 = −5x$ (див. Малюнок$\PageIndex{9}$).

Малюнок$\PageIndex{9}$: Повідомлення про графічне рішення на домашнє завдання.

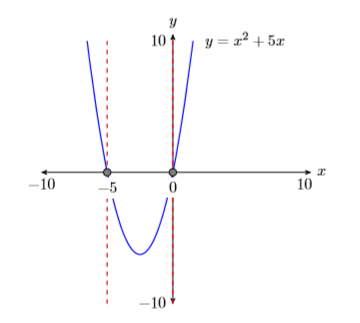
Значить, рішення$x^2 = −5x$ є$x = −5$ і$x = 0$. Зверніть увагу, наскільки добре це узгоджується з рішеннями, знайденими за допомогою алгебраїчної техніки, та рішеннями, знайденими за допомогою утиліти 5: intersect у прикладі$\PageIndex{7}$.

Вправа$\PageIndex{8}$

Використовуйте 2: нуль утиліту на графічному калькуляторі, щоб вирішити рівняння$x^2 =4x$ для$x$.

Відповідь