6.6: Стратегія факторингу

Last updated
Save as PDF

Page ID: 58314

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Коли ви концентруєтеся на факторингу проблем одного типу, після виконання декількох ви схильні входити в ритм, а решта вправ, оскільки вони схожі, здається, протікають. Однак, коли ви стикаєтеся з сумішшю факторингових проблем різних типів, прогрес складніший. Мета цього розділу - створити стратегію, яку слід дотримуватися при атаці загальної проблеми факторингу.

Якщо це ще не було зроблено, корисно розташувати терміни даного многочлена у певному порядку (за спаданням або зростанням). Тоді ви хочете застосувати наступні рекомендації.

Стратегія факторингу

Ці кроки слід дотримуватися в тому порядку, в якому вони з'являються.

Фактор з найбільшого загального фактора (\(\mathrm{GCF}\)).
Шукайте спеціальну форму.
1. Якщо у вас є два досконалих квадрата, розділених знаком мінус, використовуйте для множника різницю квадратів:\[a^2 −b^2 =(a + b)(a−b)\nonumber \]
2. Якщо у вас є триноміал, перший і останній терміни якого є ідеальними квадратами, ви повинні підозрювати, що у вас є ідеальний квадратний триноміал. Візьміть квадратні корені першого та останнього термінів та фактора наступним чином. \[a^2 +2ab + b^2 =(a + b)^2 \nonumber \]Обов'язково перевірте правильність середнього терміну.
Якщо у вас є триноміал форми\(ax^2 + bx + c\), використовуйте\(ac\) метод -method to factor.
Якщо у вас є чотиричленний вираз, спробуйте коефіцієнт шляхом групування.

Після того, як ви застосували вищевказану стратегію до даного полінома, цілком можливо, що один з ваших результуючих факторів буде впливати далі. Таким чином, ми маємо наступне правило.

Фактор повністю

Процес факторингу не завершений, доки жоден з решти факторів не може бути врахований далі. В цьому і полягає сенс фрази «фактор повністю».

Нарешті, дуже гарне слово поради.

Перевірте свій факторинг шляхом множення

Після того, як ви повністю врахували даний многочлен, це дуже хороша практика, щоб перевірити свій результат. Якщо ви помножите, щоб знайти добуток ваших факторів, і в результаті отримаєте початковий заданий многочлен, то ви знаєте, що ваша факторизація правильна.

Це трохи більше роботи, щоб перевірити вашу факторизацію, але це варте того. Це допомагає усунути помилки, а також допомагає краще зрозуміти процес факторингу. Пам'ятайте, факторинг - це «немноження», тому чим більше ви множите, тим краще отримуєте при факторингу.

Давайте подивимося, що може статися, коли ви не перевіряєте свою факторизацію!

Попередження! Наступне рішення невірно!

Фактор:\(2x^4 +8x^2\)

Рішення: Фактор з\(\mathrm{GCF}\)

\[\begin{align*} 2x^4+8x^2 &= 2x^2(x^2+4) \\ &= 2x^2(x+2)^2 \end{align*} \nonumber\]

Відзначимо, що цей учень не спромогся перевірити його факторизацію. Давайте зробимо це для нього зараз.

Перевірка: Множення для перевірки. Пам'ятайте, при квадратизації біноміала існує середній термін.

\[\begin{align*} 2x^2(x+2)^2 &= 2x^2(x^2+4x+4) \\ &= 2x^4+8x^3+8x^2 \end{align*} \nonumber\]

Це не те саме, що оригінальний многочлен\(2x^4 +8x^2\), тому факторизація учня неправильна. Якби студент виконав цю перевірку, він міг би зловити свою помилку, за умови, звичайно, що він правильно розмножується під час перевірки.

Далі слід правильна факторизація.

\[\begin{align*} 2x^4+8x^2 &= 2x^2(x^2+4) \\ \end{align*} \nonumber\]

Сума квадратів не множник, тому ми закінчили.

Перевірка: Множення для перевірки.

\[\begin{align*} 2x^2(x^2+4) &= 2x^4+8x^2\\ \end{align*} \nonumber\]

Це те ж саме, що і початковий многочлен\(2x^4 +8x^2\), тому ця факторизація є правильною.

Приклад\(\PageIndex{1}\)

Фактор повністю:\(−3x^6 +3x^2\)

Рішення

Перше правило факторингу — «Фактор з GCF». \(\mathrm{GCF}\)З\(−3x^6\) і\(3x^2\) є\(3x^2\), так що ми могли б враховувати\(3x^2\). \[−3x^6 +3x^2 =3x^2(−x^4 + 1) \nonumber \]Це цілком справедливо, але нам не подобається той факт, що другий фактор починається з\(−x^4\). Давайте перерахуємо\(−3x^2\) замість цього. \[−3x^6 +3x^2 = −3x^2(x^4 −1) \nonumber \]Другий фактор - різниця двох квадратів. Візьміть квадратні коріння, відокремлюючи одну пару зі знаком плюс, одну пару зі знаком мінус. \[= −3x^2(x^2 + 1)(x^2 −1) \nonumber \]Сума квадратів не множник. Але останній фактор - різниця двох квадратів. Візьміть квадратні коріння, відокремлюючи одну пару зі знаком плюс, одну пару зі знаком мінус. \[= −3x^2(x^2 + 1)(x + 1)(x−1) \nonumber \]

Перевірка: Множте, щоб перевірити результат.

\[\begin{align*} -3x^2(x^2+1)(x+1)(x-1) &= -3x^2(x^2+1)(x^2-1)\\ &= -3x^2(x^4-1)\\ &= -3x^6+3x^2 \end{align*} \nonumber\]

Перевірки факторизації.

Вправа\(\PageIndex{1}\)

Фактор повністю:\(−4x^7 + 64x^3\)

Відповідь: \(−4x^3(x^2 + 4)(x + 2)(x−2)\)

Приклад\(\PageIndex{2}\)

Фактор повністю:\(x^3y +9xy^3 +6x^2y^2\)

Рішення

Перше правило факторингу — «Фактор з GCF». \(\mathrm{GCF}\)З\(x^3y\), і\(6x^2y^2\) є\(9xy^3\)\(xy\), так що ми враховуємо\(xy\). \[x^3y +9xy^3 +6x^2y^2 = xy(x^2 +9y^2 +6xy) \nonumber \]Давайте розпоряджаємо, що другий фактор у спадних повноваженнях\(x\). \[= xy(x^2 +6xy +9y^2) \nonumber \]Перший і останній члени триноміального коефіцієнта є досконалими квадратами. Ми підозрюємо, що у нас є ідеальний квадратний триноміал, тому беремо квадратні корені першого та останнього термінів, перевіряємо середній термін і пишемо:\[= xy(x +3y)^2 \nonumber \] Таким чином,\(x^3y +9xy^3 +6x^2y^2 = xy(x +3y)^2\).
Перевірка: Множте, щоб перевірити результат. \[\begin{align*} xy(x+3y)^2 &= xy(x^2 +6xy +9y^2)\\ &= x^3y+6x^2y^2 +9xy^3 \end{align*} \nonumber\]
За винятком порядку, цей результат такий же, як і заданий многочлен. Перевірки факторизації.

Вправа\(\PageIndex{2}\)

Фактор повністю:\(3a^2b^4 + 12a^4b^2 −12a^3b^3\)

Відповідь: \(3a^2b^2(2a−b)^2\)

Приклад\(\PageIndex{3}\)

Фактор повністю:\(2x^3 −48x + 20x^2\)

Рішення

В останньому прикладі ми визнали необхідність переставляти наші умови після того, як ми витягли\(\mathrm{GCF}\). Цього разу, давайте розставимо наші умови в спадних\(x\) повноваженнях відразу. \[2x^3 −48x + 20x^2 =2x^3 + 20x^2 −48x \nonumber \]Тепер давайте врахуємо\(\mathrm{GCF}\). \[=2x(x^2 + 10x−24) \nonumber \]Останній термін триноміального фактора не є ідеальним квадратом. Перейдемо до ac-методу до фактора. Пара цілих чисел\(−2,12\) має добуток рівний\(ac = −24\) і суму, рівну\(b = 10\). Оскільки коефіцієнт\(x^2\) є одним, це ситуація «падіння на місці». Ми кидаємо нашу пару на місце і пишемо:\[=2x(x−2)(x + 12) \nonumber \] Таким чином,\(2x^3 −48x + 20x^2 =2x(x−2)(x + 12)\).

Перевірка: Множте, щоб перевірити результат. Ми використовуємо ярлик методу FOIL та розумові розрахунки, щоб прискорити ситуацію. \[\begin{align*} 2x(x-2)(x + 12) &= 2x(x^2+10x-24) \\ &= 2x^3 + 20x^2 - 48x \end{align*} \nonumber\]За винятком порядку, цей результат такий же, як і заданий многочлен. Перевірки факторизації.

Вправа\(\PageIndex{3}\)

Додайте сюди текст вправ.

Відповідь: \(−3x^2(x−4)(x−5)\)

Приклад\(\PageIndex{4}\)

Фактор повністю:\(2a^2 −13ab−24b^2\)

Рішення

Немає загального фактора, який ми можемо врахувати. У нас є триноміал, але перший і останній терміни не є ідеальними квадратами, тому давайте застосуємо\(ac\) метод -method. Ігноруючи змінні на мить, нам потрібна ціла пара, добуток якої\(ac = −48\) і чия сума дорівнює\(−13\). Пара цілих чисел\(3,−16\) приходить на розум (якщо нічого не спадає на думку, почніть перераховувати цілочисельні пари). Розбийте середній член на суму подібних термінів, використовуючи цілу пару\(3,−16\), а потім множник шляхом групування

\[\begin{align*} 2a^2-13ab-24b^2 &= 2a^2 +3ab-16ab-24b^2 \\ &= a(2a+3b)-8b(2a+3b)\\ &= (a-8b)(2a+3b) \end{align*} \nonumber\]

Таким чином,\(2a^2-13ab-24b^2 =( a−8b)(2a +3 b)\).

Перевірка: Множте, щоб перевірити результат. Ми використовуємо ярлик методу FOIL та розумові розрахунки, щоб прискорити ситуацію. \[(a−8b)(2a +3 b)=2a^2 −13ab−24b^2 \nonumber \]Цей результат такий же, як і заданий многочлен. Перевірки факторизації.

Вправа\(\PageIndex{4}\)

Фактор повністю:\(8x^2 + 14xy−15y^2\)

Відповідь: \((2 x +5y)(4x−3y)\)

Приклад\(\PageIndex{5}\)

Фактор повністю:\(30x^4 + 38x^3 −20x^2\)

Рішення

Першим кроком є врахування того\(\mathrm{GCF}\), що в даному випадку є\(2x^2\). \[30x^4 + 38x^3 −20x^2 =2x^2(15x^2 + 19x−10) \nonumber \]Перший і останній члени триноміального коефіцієнта не є досконалими квадратами, тому давайте знову перейдемо до\(ac\) -методу. Порівнюючи\(15x^2+19x−10\) з\(ax^2+bx+c\), зверніть увагу, що\(ac = (15)(−10) = −150\). Нам потрібна ціла пара, добуток якої\(−150\) і чия сума дорівнює\(19\). Пара цілих чисел\(−6\) і\(25\) задовольняє цим вимогам. \(a \neq 1\)Тому що це не ситуація «падіння на місці», тому нам потрібно розбити середній термін як суму подібних термінів, використовуючи пару\(−6\) і\(25\). \[=2x^2(15x^2 −6x + 25x−10) \nonumber \]Фактор за групуванням. Фактор\(3x\) з перших двох термінів і\(5\) з третього та четвертого. \[=2x^2(3x(5x−2) + 5(5x−2)) \nonumber \]Нарешті, враховуйте загальний фактор\(5x−2\). \[=2x^2(3x + 5)(5x−2) \nonumber \]Таким чином,\(30x^4 + 38x^3 −20x^2 =2x^2(3x + 5)(5x−2)\).

Перевірка: Множте, щоб перевірити результат. Скористайтеся методом FOIL, щоб спочатку помножити біноміали. \[2x^2(3x + 5)(5x−2) = 2x^2(15x^2 + 19x−10) \nonumber \]Розподіліть\(2x^2\). \[= 30x^4 + 38x^3 −20x^2 \nonumber \]Цей результат такий же, як і заданий многочлен. Перевірки факторизації.

Вправа\(\PageIndex{5}\)

Фактор повністю:\(36x^3 + 60x^2 +9x\)

Відповідь: \(3x(6x + 1)(2x + 3)\)

Приклад\(\PageIndex{6}\)

Фактор повністю:\(8x^5 + 10x^4 −72x^3 −90x^2\)

Рішення

Кожен з термінів ділиться на\(3x^3\). Фактор вихід\(3x^3\). \[15x^6 −33x^5 −240x^4 + 528x^3 =3x^3[5x^3 −11x^2 −80x + 176] \nonumber \]Другий фактор - це чотиричленний вираз. Фактор за групуванням.

\[\begin{align*} &= 3x^3[x^2(5x-11)-16(5x-11)] \\ &= 3x^3(x^2-16)(5x-11) \end{align*} \nonumber\]

Коефіцієнт\(x^2−16\) - це різниця двох квадратів. Візьміть квадратні коріння, відокремте одну пару плюсом, одну пару з мінусом. \[=3x^3(x + 4)(x−4)(5x−11) \nonumber \]Таким чином,\(15x^6 −33x^5 −240x^4 + 528x^3 =3x^3(x + 4)(x−4)(5x−11)\).

Перевірка: Множте, щоб перевірити результат.

\[\begin{align*} 3x^3(x + 4)(x-4)(5x-11) &= 3x^3(x^2-16)(5x-11) \\ &= 3x^3(5x^3 - 11x^2 - 80x + 176 \\ &= 15x^6 - 33x^5 - 240x^4 + 528x^3 \end{align*} \nonumber\]

Цей результат такий же, як і заданий многочлен. Перевірки факторизації.

Вправа\(\PageIndex{6}\)

Фактор повністю:\(15x^6−33x^5−240x^4 +528x^3\)

Відповідь: \(2x^2(x−3)(x + 3)(4x + 5)\)

Використання калькулятора для допомоги\(ac\) -Method

При використанні\(ac\) -method для множника\(ax^2+bx+c\) і\(ac\) є дуже великим числом, то може бути важко знайти пару, твір якої є\(ac\) і сума якої в\(b\). Для прикладу розглянемо триноміал:\[12y^2 −11y−36 \nonumber \] Нам потрібна ціла пара, добуток якої\(ac =−432\) і чия сума дорівнює\(b = −11\). Ми починаємо перераховувати цілочисельні можливості пари, але процес швидко стає складним.

\[\begin{array}{l} 1,-432\\ 2,-216\\ \quad\dots \end{array} \nonumber \]

Зауважте, що числа у другому стовпці можна знайти\(ac =−432\) шляхом ділення на число у першому стовпці. Тепер ми будемо використовувати цей факт і функцію ТАБЛИЦЯ на нашому калькуляторі, щоб переслідувати бажану цілу пару.

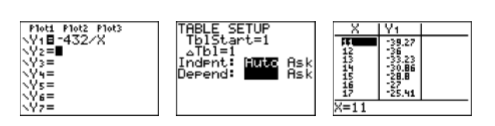
Введіть вираз\(-432/X\)\(\mathbb{Y1}\) в меню Y= (див. перше зображення на малюнку\(\PageIndex{1}\)).
Над кнопкою WINDOW ви побачите TBLSET. За допомогою 2-ї клавіші, потім натисніть кнопку WINDOW, щоб отримати доступ до меню, показаного на другому зображенні малюнка\(\PageIndex{1}\). Встановіть tblStart=1\(\triangle \text {Tbl}=1\), а потім виділіть AUTO як для незалежних, так і для залежних змінних.
Над кнопкою GRAPH ви побачите ТАБЛИЦЮ. Використовуйте 2-ю клавішу, потім натисніть кнопку GRAPH, щоб отримати доступ до таблиці, показаної на третьому зображенні на малюнку\(\PageIndex{1}\). Використовуйте клавіші зі стрілками вгору і вниз для прокрутки вмісту таблиці. Зауважте, що ви можете ігнорувати більшість пар, оскільки вони не є цілими числами. Звертайте увагу тільки тоді, коли вони обидва цілі числа. При цьому пам'ятайте, що ви шукаєте пару, сума якої дорівнює\(b = −11\). Зверніть увагу, що пара,\(16,−27\) показана на третьому зображенні малюнка,\(\PageIndex{1}\) є парою, яку ми шукаємо.

рис. 6.6.1.png — Малюнок\(\PageIndex{1}\): Використання функції **TABLE** для допомоги\(ac\) методу -method.

Тепер ми можемо розбити середній член на суму подібних термінів, використовуючи\(12y^2 −11y −36\) впорядковану пару\(16,−27\), а потім множник шляхом групування.

\[\begin{align*} 12y^2-11y-36 &= 12y^2 + 16y-27y-36\\ &= 4y(3y + 4)-9(3y + 4) \\ &= (4y-9)(3y+4) \end{align*} \nonumber \]

Перевірка: Використовуйте ярлик методу FOIL та розумові обчислення для множення. \[(4y−9)(3y + 4) = 12y^2 −11y−36 \nonumber \]Перевірки факторизації.