6.5: Факторингові спеціальні форми

Last updated
Save as PDF

Page ID: 58302

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У цьому розділі ми переглядаємо дві спеціальні форми продукту, які ми дізналися в главі 5, перший з яких був квадрат біном.

Квадратування біноміального

Ось два більш ранніх правила для квадратизації біноміала.

$(a + b)^2 = a^2 +2ab + b^2$
$(a−b)^2 = a^2 −2ab + b^2$

Ідеальні квадратні триноми

Щоб зробити квадрат біном типу$(a + b)^2$, дійте наступним чином:

Квадратний перший термін:$a$
Помножте перший і другий члени, потім подвоїте:$2ab$
Квадратний останній термін:$b^2$

Приклад$\PageIndex{1}$

Розгорнути:$(2x +3y)^2$

Рішення

Використовуючи викрійку$(a+b)^2 = a^2+2ab+b^2$, ми можемо розширити$(2x+3y)^2$ наступним чином:

\[\begin{align*} (2x +3y)^2 &= (2x)^2 + 2(2x)(3y) + (3y)^2 \\ &= 4x^2 +6xy +9y^2 \end{align*} \nonumber \]

Зверніть увагу, як ми квадратизуємо перший і другий члени, а потім виробляємо середній термін нашої відповіді, множивши перший і другий члени і подвоюючи.

Вправа$\PageIndex{1}$

Розгорнути:$(5a +2b)^2$

Відповідь: $25a^2 + 20ab +4b^2$

Приклад$\PageIndex{2}$

Розгорнути:$(3u^2 −5v2)^2$

Рішення

Використовуючи викрійку$(a−b)^2 = a^2−2ab+b^2$, ми можемо розширити$(3u^2−5v^2)^2$ наступним чином:

\[\begin{align*} (3u^2 -5v^2)^2 &= (3u^2)^2 - 2(3u^2)(5v^2) + (5v^2)^2 \\ &= 9u^4 - 30u^2v^2 + 25v^4 \end{align*} \nonumber \]

Зверніть увагу, що ознака середнього терміну на цей раз негативний. Перший і останній терміни все ще позитивні, тому що ми в квадраті.

Вправа$\PageIndex{2}$

Розгорнути:$(2s^3 −7t)^2$

Відповідь: $4s^6 −28s^3t + 49t^2$

Після того, як ви склали кілька біноміалів, настав час виконати всю роботу у вашій голові.

Квадратний перший термін.
Помножте перший і другий члени і подвоюйте результат.
Квадратний другий член.

Приклад$\PageIndex{3}$

Розгорніть кожне з наведених нижче дій:

$(2y−3)^2$
$(4a−3b)^2$
$(x3 + 5)^2$

Рішення

Використовуючи викрійку$(a ± b)^2 = a^2 ± 2ab + b^2$, розширюємо кожну біноміально подумки, записуючи відповідь без будь-яких проміжних кроків.

$(2y−3)^2 = 4y^2 −12y +9$
$(4a−3b)^2 = 16a^2 −24ab +9b^2$
$(x^3 + 5)^2 = x^6 + 10x^3 + 25$

Вправа$\PageIndex{3}$

Розгорнути:$(5x^4 −3)^2$

Відповідь: $25x^8 −30x^4 +9$

Тепер, оскільки факторинг - це «немноження», це має бути простою справою, щоб змінити процес Example$\PageIndex{3}$.

Приклад$\PageIndex{4}$

Фактор кожного з наступних триноміалів:

$4y^2 −12y + 9$
$16a^2 −24ab +9b^2$
$x^6 + 10x^3 + 25$

Рішення

Через роботу, яка вже виконана в прикладі$\PageIndex{3}$, це просте завдання, щоб врахувати кожен з цих триноміалів.

$4y^2 −12y + 9 = (2y−3)^2$
$16a^2 −24ab +9b^2 = (4 a−3b)^2$
$x^6 + 10x^3 + 25 = (x^3 + 5)$

Вправа$\PageIndex{4}$

Фактор:$25x^8 −30x^4 +9$

Відповідь: $(5x^4 −3)^2$

Кожен з триноміалів у Прикладі$\PageIndex{4}$ є прикладом ідеального квадратного триноміала.

Ідеальний квадратний триноміал

Якщо тріноміал$a^2 +2ab + b^2$ - це квадрат двочлена, як в$(a+b)^2$, то тріноміал називається досконалим квадратним тріноміалом.

Отже, як розпізнати ідеальний квадратний триноміал? Якщо перший і останній терміни триноміалу є ідеальними квадратами, то ви повинні підозрювати, що ви можете мати справу з ідеальним квадратним тріноміалом. Однак ви також повинні мати правильний середній термін, щоб мати ідеальний квадратний триноміал.

Таблиця$\PageIndex{1}$: Список квадратів
$n$	$n^2$
\ (n\) ">1	\ (n^2\) ">1
\ (n\) ">2	\ (n^2\) ">4
\ (n\) ">3	\ (n^2\) ">9
\ (n\) ">4	\ (n^2\) ">16
\ (n\) ">5	\ (n^2\) ">25
\ (n\) ">6	\ (n^2\) ">36
\ (n\) ">7	\ (n^2\) ">49
\ (n\) ">8	\ (n^2\) ">64
\ (n\) ">9	\ (n^2\) ">81
\ (n\) ">10	\ (n^2\) ">100
\ (n\) ">11	\ (n^2\) ">121
\ (n\) ">12	\ (n^2\) ">144
\ (n\) ">13	\ (n^2\) ">169
\ (n\) ">14	\ (n^2\) ">196
\ (n\) ">15	\ (n^2\) ">225
\ (n\) ">16	\ (n^2\) ">256
\ (n\) ">17	\ (n^2\) ">289
\ (n\) ">18	\ (n^2\) ">324
\ (n\) ">19	\ (n^2\) ">361
\ (n\) ">20	\ (n^2\) ">400
\ (n\) ">21	\ (n^2\) ">441
\ (n\) ">22	\ (n^2\) ">484
\ (n\) ">23	\ (n^2\) ">529
\ (n\) ">24	\ (n^2\) ">576
\ (n\) ">25	\ (n^2\) ">625

Приклад$\PageIndex{5}$

Фактор кожного з наступних триноміалів:

$9x^2 −42x + 49$
$49a^2 + 70ab + 25b^2$
$4x^2 −37x +9$

Рішення

Зауважте, що перший і останній члени кожного триноміалу є ідеальними квадратами.

У триноміалі зверніть увагу$9x^2−42x+49$, що$(3x)^2 =9x^2$ і$72 = 49$. Отже, перший і останній терміни є ідеальними квадратами. Беручи квадратні корені, ми підозрюємо, що$9x^2 −42x + 49$ фактори такі:\[9x^2 −42x + 49 \overset{?}{=} (3x−7)^2 \nonumber \] Однак ми повинні перевірити, чи правильний середній термін. Помножити$3x$ і$7$, потім подвоїти:$2(3x)(7) = 42x$. Таким чином, середній термін є правильним і тому\[9x^2 −42x + 49 = (3x−7)^2\nonumber \]
У триноміалі зверніть увагу$49a^2+70ab+25b^2$, що$(7a)^2 = 49a^2$ і$(5b)^2 = 25 b^2$. Отже, перший і останній терміни є ідеальними квадратами. Беручи квадратні корені, ми підозрюємо, що$49a^2 + 70ab + 25 b^2$ фактори такі:\[49a^2 + 70ab + 25 b^2 \overset{?}{=} (7 a +5 b)^2 \nonumber \] Однак ми повинні перевірити, чи правильний середній термін. Помножити$7a$ і$5b$, потім подвоїти:$2(7a)(5b) = 70ab$. Таким чином, середній термін є правильним і тому\[49a^2 + 70ab + 25 b^2 = (7 a +5 b)^2 \nonumber \]
У триноміалі зверніть увагу$4x^2−37x+9$, що$(2x)^2 =4x^2$ і$(3)^2 = 9$. Отже, перший і останній терміни є ідеальними квадратами. Беручи квадратні коріння, підозрюємо, що$4x^2 −37x + 9$ фактори такі:\[4x^2 −37x +9 \overset{?}{=} (2x−3)^2 \nonumber \]

Однак ми повинні перевірити, чи правильний середній термін. Помножити$2x$ і$3$, потім подвоїти:$2(2x)(3) = 12x$. Однак це не середній термін$4x^2 −37x + 9$, тому ця факторизація невірна! Ми повинні знайти інший спосіб фактора цього триміналу.

Порівнюючи$4x^2 −37x+ 9$ з$ax^2 + bx+ c$, нам потрібна пара цілих чисел, добуток яких$ac = 36$ і сума яких дорівнює$b = −37$. Ціла пара$−1$ і$−36$ приходить на розум. Замініть середній член як суму подібних термінів, використовуючи цю впорядковану пару.

\[\begin{align*} 4x^2-37x +9 &= 4x^2-x-36x +9 \quad \color {Red} -37x=-x-36x\\ &= x(4x-1)-9(4x-1) \quad \color {Red} \text {Factor by grouping}\\ &= (x-9)(4x-1) \quad \color {Red} \text {Factor out } 4x-1 \end{align*} \nonumber \]

Цей приклад наочно демонструє, наскільки важливо перевірити середньострокову перспективу.

Вправа$\PageIndex{5}$

Фактор:$16x^2 + 72x + 81$

Відповідь: $(4x + 9)^2$

Пам'ятайте перше правило факторингу!

Перше правило факторингу

Першим кроком для виконання в будь-якій проблемі факторингу є фактор$\mathrm{GCF}$.

Приклад$\PageIndex{6}$

Фактор кожного з наступних триноміалів:

$2x^3y + 12x^2y^2 + 18xy^3$
$−4x^5 + 32x^4 −64x^3$

Рішення

Пам'ятайте, перший фактор з$\mathrm{GCF}$.

У триноміалі відзначимо$2x^3y + 12x^2y^2 + 18xy^3$, що$\mathrm{GCF}$ of$2x^3y$$12x^2y^2$, і$18xy^3$ є$2xy$. Спочатку ми враховуємо$2xy$. \[2x^3y + 12x^2y^2 + 18xy^3 =2xy(x^2 +6xy +9y^2) \nonumber \]Тепер зауважимо, що перший і останній члени отриманого триноміального коефіцієнта є ідеальними квадратами, тому ми приймаємо їх квадратні корені та фактори наступним чином. \[=2xy(x +3y)^2 \nonumber \]Звичайно, остання факторизація є правильною тільки в тому випадку, якщо середній термін правильний. Оскільки$2(x)(3y)=6xy$ збігається з середнім терміном$x^2 +6xy +9y^2$, у нас є ідеальний квадратний триноміал, і наш результат правильний.
У триноміалі відзначимо$−4x^5 + 32x^4 −64x^3$, що$\mathrm{GCF}$ of$4x^5$$32x^4$, і$64x^3$ є$4x^3$. Спочатку ми враховуємо$4x^3$. \[−4x^5 + 32x^4 −64x^3 =4x^3(−x^2 +8x−16) \nonumber \]Однак перший і третій члени$−x^2 +8x−16$ є негативними, і, отже, не є ідеальними квадратами. Давайте почнемо знову, на цей раз факторинг$−4x^3$. \[−4x^5 + 32x^4 −64x^3 = −4x^3(x^2 −8x + 16) \nonumber \]Цього разу перший і третій члени$x^2−8x+16$ - ідеальні квадрати. Беремо їх квадратні корені і пишемо:\[= −4x^3(x−4)^2 \nonumber \] Знову ж таки, ця остання факторизація є правильною лише в тому випадку, якщо середній член правильний. $2(x)(4) = 8x$Тому що у нас є ідеальний квадратний триноміал, і наш результат правильний.

Вправа$\PageIndex{6}$

Фактор:$−4x^3 −24x^2 −36x$

Відповідь: $−4x(x + 3)^2$

Різниця квадратів

Друга спеціальна форма продукту, яку ми дізналися в главі 5, була різниця квадратів.

Різниця квадратів

Ось відмінність квадратів правило. \[(a + b)(a−b)=a^2 − b^2 \nonumber \]

Якщо ви множите два біноміали, які мають однакові члени в позиціях «Перший» і точно такі ж члени в позиціях «Останній», але один множник розділений знаком плюс, а інший множник розділений знаком мінус, то множте наступним чином:

Квадратний перший термін:$a^2$
Квадратний другий член:$b^2$
Помістіть знак мінус між двома квадратами.

Приклад$\PageIndex{7}$

Розгорніть кожне з наведених нижче дій:

$(3x+5)(3x-5)$
$(a^3 −2b^3)(a^3 +2b^3)$

Рішення

Застосовуємо різницю квадратів шаблону, щоб розширити кожну з заданих задач.

В$(3x + 5)(3x − 5)$, ми маємо точно такі ж терміни в позиціях «Перший» і «Останній», причому перший набір розділений знаком плюс, а другий набір розділений знаком мінус.
1. Квадратний перший термін:$(3x)^2 =9x^2$
2. Квадратний другий член:$5^2 = 25$
3. Помістіть знак мінус між двома квадратами.

Звідси:\[(3x + 5)(3x−5) = 9x^2 −25 \nonumber \]

В$(a^3 −2b^3)(a^3 +2b^3)$, ми маємо точно такі ж терміни в позиціях «Перший» і «Останній», причому перший набір розділений знаком мінус, а другий набір розділений знаком плюс.
1. Квадратний перший термін:$(a^3)^2 = a^6$
2. Квадратний другий член:$(2b^3)^2 =4b^6$
3. Помістіть знак мінус між двома квадратами.

Звідси:\[(a^3 −2b^3)(a^3 +2b^3)=a^6 −4b^6 \nonumber \]

Вправа$\PageIndex{7}$

Розгорнути:$(4x−3y)(4x +3y)$

Відповідь: $16x^2 −9y^2$

Оскільки факторинг - це «немноження», це має бути простою справою, щоб змінити процес Приклад$\PageIndex{7}$.

Приклад$\PageIndex{8}$

Коефіцієнт кожного з наступних дій:

$9x^2 −25$
$a^6 −4b^6$

Рішення

Через роботу, вже виконану в прикладі$\PageIndex{7}$, це проста справа, щоб коефіцієнт (або «помножити») кожну з цих проблем.

$9x^2 −25 = (3x + 5)(3x−5)$
$a^6 −4b^6 =(a^3 −2b^3)(a^3 +2b^3)$

У кожному випадку зверніть увагу на те, як ми взяли квадратні коріння кожного члена, потім відокремлювали один набір знаком плюс, а інший - знаком мінус. Через комутативного властивості множення неважливо, який з них ви робите плюс, а який робите мінус.

Вправа$\PageIndex{8}$

Фактор:$81x^2 −49$

Відповідь: $(9x + 7)(9x−7)$

Завжди пам'ятайте перше правило факторингу.

Приклад$\PageIndex{9}$

Фактор:$x^3 −9x$

Рішення

В$x^3 −9x$,$\mathrm{GCF}$ з$x^3$ і$9x$ є$x$. Фактор вихід$x$. \[x^3−9x = x(x^2 −9) \nonumber \]Зверніть увагу,$x^2−9$ що тепер різниця двох ідеальних квадратів. Візьміть квадратні коріння$x^2$ і$9$, які є$x$ і$3$, потім відокремте один набір знаком плюс, а інший поставте зі знаком мінус.
\[= x(x + 3)(x−3) \nonumber \]

Вправа$\PageIndex{9}$

Фактор:$4x^4−16x^2$

Відповідь: $4x^2(x + 2)(x−2)$

Факторинг повністю

Іноді після одного проходу при факторингу залишаються фактори, які можуть бути враховані далі. Ви повинні продовжувати враховувати в цьому випадку.

Приклад$\PageIndex{10}$

Фактор:$x^4 −16$

Рішення

В$x^4 −16$, у нас є різниця двох квадратів:$(x^2)^2 = x^4$ і$4^2 = 16$. Спочатку беремо квадратні коріння, потім відокремлюємо один набір знаком плюс, а інший встановлюємо зі знаком мінус. \[x^4 −16 = (x^2 + 4)(x^2 −4) \nonumber \]Зверніть увагу, що$x^2+4$ це сума двох квадратів і не множиться далі. Однак$x^2 −4$ є різниця двох квадратів. Візьміть квадратні коріння$2$,$x$ а, потім відокремте один набір знаком плюс, а інший поставте зі знаком мінус.
\[=( x^2 + 4)(x + 2)(x−2) \nonumber \]Готово. Ми не можемо враховувати далі.

Вправа$\PageIndex{10}$

Фактор:$x^4 −81$

Відповідь: $(x^2 + 9)(x + 3)(x−3)$

Нелінійні рівняння переглянуті

Пам'ятайте, якщо рівняння нелінійне, перший крок - зробити одну сторону рівною нулю, перемістивши всі члени в одну сторону рівняння. Після того, як ви виконаєте цей важливий перший крок, врахуйте та застосуйте властивість нульового продукту, щоб знайти рішення.

Приклад$\PageIndex{11}$

Вирішити для$x$:$25x^2 = 169$

Рішення

Зробіть одну сторону рівною нулю, коефіцієнт, потім застосуйте властивість нульового добутку.

\[\begin{align*} 25x^2 &= 169 \quad \color {Red} \text {Original equation.}\\ 25x^2 - 169 &= 0 \quad \color {Red} \text {Subtract 169 from both sides.} \end{align*} \nonumber \]

Зверніть увагу, що у нас є два ідеальних квадрата, розділених знаком мінус. У цьому і полягає відмінність малюнка квадратів. Візьміть квадратні коріння, зробивши один член плюс і один термін мінус.

\[\begin{align*} (5x + 13)(5x-13) &= 0 \quad \color {Red} \text {Use difference of squares to factor.} \end{align*} \nonumber \]

Використовуйте властивість нульового добутку для завершення рішення, встановивши кожен коефіцієнт рівним нулю і вирішуючи отримані рівняння.

\[\begin{align*} 5x + 13 &= 0 \\ x &= -\dfrac{13}{5} \end{align*} \nonumber\]

або

\[\begin{align*} 5x - 13 &= 0 \\ x &= \dfrac{13}{5} \end{align*} \nonumber\]

Значить, рішення$25x^2 = 169$ є$x =−13/5$ і$x = 13 /5$. Ми закликаємо читачів перевірити кожне з цих рішень.

Вправа$\PageIndex{11}$

Вирішити для$x$:$16x^2 = 121$

Відповідь: $−11/4$,$11/4$

Приклад$\PageIndex{12}$

Вирішити для$x$:$49x^2 + 81 = 126x$

Рішення

Зробіть одну сторону рівною нулю, коефіцієнт, потім застосуйте властивість нульового добутку.

\[\begin{align*} 49x^2+81x &= 126x \quad \color {Red} \text {Original equation.}\\ 49x^2-126x+81 &= 0 \quad \color {Red} \text {Subtract 126x from both sides.} \end{align*} \nonumber \]

Зауважте, що перший і останній члени триноміалу є ідеальними квадратами. Отже, має сенс спробувати фактор як ідеальний квадратний триноміал, беручи квадратні коріння першого та останнього термінів.

\[\begin{align*} (7x-9)^2 &= 0 \quad \color {Red} \text {Factor as a perfect square trinomial.} \end{align*} \nonumber \]

Звичайно, обов'язково перевіряйте середньостроковий термін. Тому що$−2(7x)(9) = −126x$, середній термін є правильним. Тому що$(7x−9)^2 = (7 x−9)(7x−9)$, ми можемо використовувати властивість нульового добутку, щоб встановити кожен коефіцієнт рівний нулю і вирішити отримані рівняння.

\[\begin{align*} 7x-9 &= 0 \\ x &= \dfrac{9}{7} \end{align*} \nonumber\]

або

\[\begin{align*} 7x-9 &= 0 \\ x &= \dfrac{9}{7} \end{align*} \nonumber\]

Отже, єдиним рішенням$49x^2 +81 = 126x$ є$x =9 /7$. Ми закликаємо читачів перевірити це рішення.

Примітка

Можна також стверджувати, що єдине число, квадрат якого дорівнює нулю, - це число нуль. Отже, можна переходити безпосередньо від$(7x−9)^2 =0$ до$7x−9=0$. Отже, єдиним рішенням$49x^2 + 81 = 126x$ є$x =9 /7$.

Вправа$\PageIndex{12}$

Вирішити для$x$:$25x^2 = 80x−64$

Відповідь: $8/5$

Приклад$\PageIndex{13}$

Вирішити для$x$:$2x^3 +3x^2 = 50x + 75$

Рішення

Зробіть одну сторону рівною нулю, коефіцієнт, потім застосуйте властивість нульового добутку.

\[\begin{align*} 2x^3 +3x^2 &= 50x + 75 \quad \color {Red} \text {Original equation.}\\ 2x^3 + 3x^2 - 50x - 75 &= 0 \quad \color {Red} \text {Make one side zero.} \end{align*} \nonumber \]

Це чотиритерміновий вираз, тому ми намагаємося факторинг шляхом групування. Коефіцієнт$x^2$ з перших двох термінів, а$−25$ з другого двох термінів.

\[\begin{align*} x^2(2x + 3)-25(2x + 3) &= 0 \quad \color {Red} \text {Factor by grouping}\\ (x^2-25)(2x + 3) &= 0 \quad \color {Red} \text {Factor out } 2x+3 \end{align*} \nonumber\]

Завершіть факторизацію, використовуючи різницю квадратів до фактора$x^2−25$.

\[\begin{align*} (x+5)(x-5)(2x+3) &= 0 \quad \color {Red} \text {Use difference of squares to factor.} \end{align*} \nonumber \]

Нарешті, використовуйте властивість нульового продукту. Встановіть кожен коефіцієнт рівним нулю і вирішуйте для$x$.

\[\begin{align*} x+5 &= 0 \\ x &= -5 \end{align*} \nonumber\]

або

\[\begin{align*} x-5 &= 0 \\ x &= 5 \end{align*} \nonumber\]

або

\[\begin{align*} 2x+3 &= 0 \\ x &= -\dfrac{3}{2} \end{align*} \nonumber\]

Отже, рішення$2x^3 +3x^2 = 50x+75$ є$x = −5$$x = 5$, і$x = −3/2$. Ми закликаємо читачів перевірити кожне з цих рішень.

Вправа$\PageIndex{13}$

Вирішити для$x$:$5x^3 + 36 =x^2 + 180x$

Відповідь: $−6$,$6$,$1/5$

Розв'яжемо інше нелінійне рівняння, що відповідає алгебраїчному та графічному розв'язкам.

Приклад$\PageIndex{14}$

Вирішіть рівняння$x^3 =4x$, як алгебраїчно, так і графічно, а потім порівняйте свої відповіді.

Рішення

Зверніть увагу, що ми маємо ступінь$x$ більше одиниці, тому рівняння$x^3 =4x$ нелінійне. Зробіть одну сторону нуль і коефіцієнт.

\[\begin{align*} x^3 &= 4x \quad \color {Red} \text {Original equation.}\\ x^3-4x &= 0 \quad \color {Red} \text {Nonlinear. Make one side zero. }\\ x(x^2-4) &=0 \quad \color {Red} \text {Factor out GCF.}\\ x(x+2)(x-2) &= 0 \quad \color {Red} \text {Apply difference of squares.} \end{align*} \nonumber\]

Зверніть увагу, що тепер у нас є добуток трьох факторів, що дорівнює нулю. Властивість нульового продукту говорить про те, що хоча б один з цих факторів повинен дорівнювати нулю.

\[\begin{align*} x &= 0 \end{align*} \nonumber\]

або

\[\begin{align*} x+2 &= 0 \\ x &= -2 \end{align*} \nonumber\]

або

\[\begin{align*} x-2 &= 0 \\ x &= 2 \end{align*} \nonumber\]

Отже, рішення$x^3 =4x$ є$x = 0$$x = −2$, і$x = 2$.

Графічне рішення

Завантажте$y = x^3$$\mathbb{Y1}$ та$y =4x$$\mathbb{Y2 }$ в меню Y = вашого калькулятора. Виберіть 6:ZStandard в меню ZOOM, щоб створити графік на малюнку$\PageIndex{1}$.

Хоча зображення на малюнку$\PageIndex{1}$ показує всі три точки перетину, регулюючи параметри ВІКНА, як показано на малюнку$\PageIndex{2}$, тоді натискання кнопки GRAPH створить більш приємний вигляд точок перетину, як показано на малюнку праворуч на малюнку на малюнках. $\PageIndex{2}$.

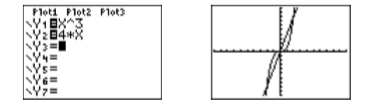
рис. 6.5.1.png — Малюнок$\PageIndex{1}$: Ескіз$y = x^3$ і$y =4x$.

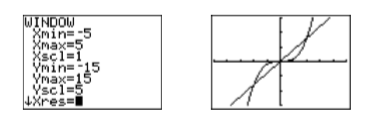
рис. 6.5.2.png — Малюнок$\PageIndex{2}$: Налаштування оглядового вікна.

Використовуйте інструмент 5: перетин з меню CALC, щоб знайти три точки перетину. Натисніть клавішу ENTER у відповідь на «Перша крива», потім натисніть клавішу ENTER ще раз у відповідь на «Друга крива», потім за допомогою клавіші зі стрілкою вліво перемістіть курсор близько до крайньої лівої точки перетину та натисніть ENTER у відповідь на «Вгадати». Результат показаний на першому зображенні зліва на малюнку$\PageIndex{3}$. Повторіть процес, щоб знайти інші точки перетину. Результати наведені на останніх двох зображеннях на рис$\PageIndex{3}$.

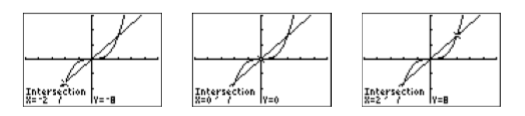
рис. 6.5.3.png — Малюнок$\PageIndex{3}$: Знаходження точок перетину.

Таким чином, графічні рішення є$x =−2$$x = 0$, і$x = 2$.

Повідомлення про рішення по домашньому завданню:

Дублюйте зображення у вікні перегляду калькулятора на сторінці домашнього завдання. Використовуйте лінійку, щоб намалювати всі лінії, але від руки будь-які криві.

Позначте горизонтальну і вертикальну$x$ осі і$y$ відповідно (див. Рис.$\PageIndex{4}$).
Розмістіть параметри WINDOW в кінці кожної осі (див. Рис.$\PageIndex{4}$).
Позначте графік його рівнянням (див. Малюнок$\PageIndex{4}$).
Пропустіть пунктирні вертикальні лінії через кожну$x$ -перехоплення. Затіньте та позначте$x$ -значення точок, де пунктирна вертикальна лінія перетинає$x$ вісь -. Це розв'язки рівняння$x^3 = 4x$ (див. Малюнок$\PageIndex{4}$).

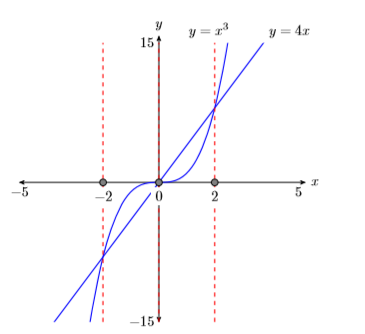
рис. 6.5.4.png — Малюнок$\PageIndex{4}$: Повідомлення про графічне рішення на домашнє завдання.

Нарешті, зверніть увагу, що графічні рішення$x = −2$$x = 0$, і$x = 2$ відповідають нашим алгебраїчним рішенням точно.

Вправа$\PageIndex{14}$

Вирішіть рівняння$x^3 = 16x$ як алгебраїчно, так і графічно, а потім порівняйте свої відповіді.

Відповідь

$−4$,$0$,$4$

$Вправа 6.5.14.png$