5.6: Множення многочленів

У цьому розділі ми знайдемо добуток поліноміальних виразів та функцій. Ми починаємо з добутку двох мономів, потім закінчимо добуток монома і полінома, і завершуємо дослідження, знайшовши добуток будь-яких двох многочленів.

Добуток мономов

Поки всі операції є множенням, ми можемо використовувати комутативні та асоціативні властивості для зміни порядку та перегрупування.

Приклад$\PageIndex{1}$

Помножити:$−5(7y)$. Спростити:$−5(7y)$.

Рішення

Використовуйте комутативні та асоціативні властивості, щоб змінити порядок і перегрупувати.

$$\begin{align*} -5(7 y) &= [(-5)(7)] y \quad &\color {Red} \text { Reorder. Regroup. } \\ &= -35 y \quad &\color {Red} \text { Multiply: } (-5)(7)=-35 \end{align*} \nonumber$$

Вправа$\PageIndex{1}$

Помножити:$3(4 x)$

Відповідь

$12x$

Приклад$\PageIndex{2}$

Помножити:$(−3x^2)(4x^3)$. Спростити:$(−3x^2)(4x^3)$.

Рішення

Використовуйте комутативні та асоціативні властивості, щоб змінити порядок і перегрупувати.

$$\begin{aligned} \left(-3 x^{2}\right)\left(4 x^{3}\right) &= [(-3)(4)]\left(x^{2} x^{3}\right) \quad \color {Red} \text { Reorder. Regroup. } \\ &= -12 x^{5} \quad \color {Red} \text { Multiply: }(-3)(4)=12, x^{2} x^{3}=x^{5}\end{aligned} \nonumber$$

Вправа$\PageIndex{2}$

Помножити:$(7 y^5)(−2y^2)$

Відповідь

$-14 y^{7}$

Приклад$\PageIndex{3}$

Помножити:$(−2a^2b^3)(−5a^3b)$. Спростити:$(−2a^2b^3)(−5a^3b)$.

Рішення

Використовуйте комутативні та асоціативні властивості, щоб змінити порядок і перегрупувати.

$$\begin{aligned} \left(-2 a^{2} b^{3}\right)\left(-5 a^{3} b\right) &=[(-2)(-5)]\left(a^{2} a^{3}\right)\left(b^{3} b\right) \quad \color {Red} \text { Reorder. Regroup. } \\ &=10 a^{5} b^{4} \quad \color {Red} \text { Multiply: }(-2)(-5)=10, a^{2} a^{3}=a^{5}, \text { and } b^{3} b=b^{4}\end{aligned} \nonumber$$

Вправа$\PageIndex{3}$

Помножити:$( −6st^2)(3s^3t^4)$

Відповідь

$-18 s^{4} t^{6}$

При множенні мономов набагато ефективніше зробити необхідні розрахунки подумки. У випадку з Приклад$\PageIndex{1}$, помножити$−5$ і$7$ подумки отримати $$−5(7y)=−35y \nonumber$$ У випадку Приклад$\PageIndex{2}$,$4$ помножити$−3$ і отримати$−12$, потім повторити базу$x$ і додати експоненти, щоб отримати $$(−3x^2)(4x^3)=−12x^5 \nonumber$$ Нарешті, у випадку Приклад$\PageIndex{3}$, $−5$множити$−2$ і отримати$10$, потім повторити бази і скласти їх показники. $$(−2a^2b^3)(−5a^3b) = 10 a^5b^4 \nonumber$$

Множення монома та многочлена

Тепер звернемо увагу на добуток монома і многочлена.

Приклад$\PageIndex{4}$

Помножити:$5\left(3 x^{2}-4 x-8\right)$

Рішення

Потрібно спочатку розподілити$5$ раз на кожен член многочлена. Потім множимо отримані мономи подумки.

$$\begin{aligned} 5\left(3 x^{2}-4 x-8\right) &=5\left(3 x^{2}\right)-5(4 x)-5(8) \\ &=15 x^{2}-20 x-40 \end{aligned} \nonumber$$

Вправа$\PageIndex{4}$

Помножити:$4\left(-2 y^{2}+3 y+5\right)$

Відповідь

$-8 y^{2}+12 y+20$

Приклад$\PageIndex{5}$

Помножити:$2 y(-3 y+5)$

Рішення

Потрібно спочатку розподілити$2y$ раз на кожен член многочлена. Потім множимо отримані мономи подумки.

$$\begin{aligned} 2 y(-3 y+5) &=2 y(-3 y)+2 y(5) \\ &=-6 y^{2}+10 y \end{aligned} \nonumber$$

Вправа$\PageIndex{5}$

Помножити:$-3 x(4-2 x)$

Відповідь

$-12 x+6 x^{2}$

Приклад$\PageIndex{6}$

Помножити:$-3 a b\left(a^{2}+2 a b-b^{2}\right)$

Рішення

Потрібно спочатку розподілити$−3ab$ раз на кожен член многочлена. Потім множимо отримані мономи подумки.

$$\begin{aligned}-3 a b\left(a^{2}+2 a b-b^{2}\right) &=-3 a b\left(a^{2}\right)+(-3 a b)(2 a b)-(-3 a b)\left(b^{2}\right) \\ &=-3 a^{3} b+\left(-6 a^{2} b^{2}\right)-\left(-3 a b^{3}\right) \\ &=-3 a^{3} b-6 a^{2} b^{2}+3 a b^{3} \end{aligned} \nonumber$$

Альтернативне рішення:

Набагато ефективніше виконувати більшість кроків продукту$−3ab(a^2 +2ab−b^2)$ подумки. Ми знаємо, що ми повинні$−3ab$ множити на кожен з членів многочлена$a^2 +2ab−b^2$. Ось наші розумові розрахунки:

1. $−3ab$раз$a^2$ дорівнює$−3a3b$.
2. $−3ab$раз$2ab$ дорівнює$−6a^2b^2$.
3. $−3ab$раз$−b^2$ дорівнює$3ab^3$.

Мислення таким чином дозволяє нам записати відповідь без жодного з кроків, показаних у нашому першому рішенні. Тобто відразу пишемо:

$$-3 a b\left(a^{2}+2 a b-b^{2}\right)=-3 a^{3} b-6 a^{2} b^{2}+3 a b^{3} \nonumber$$

Вправа$\PageIndex{6}$

Помножити:$2 x y\left(x^{2}-4 x y^{2}+7 x\right)$

Відповідь

$2 x^{3} y-8 x^{2} y^{3}+14 x^{2} y$

Приклад$\PageIndex{7}$

Помножити:$-2 z^{2}\left(z^{3}+4 z^{2}-11\right)$

Рішення

Потрібно спочатку розподілити$−2z^2$ раз на кожен член многочлена. Потім множимо отримані мономи подумки.

$$\begin{aligned}-2 z^{2}\left(z^{3}+4 z^{2}-11\right) &=-2 z^{2}\left(z^{3}\right)+\left(-2 z^{2}\right)\left(4 z^{2}\right)-\left(-2 z^{2}\right)(11) \\ &=-2 z^{5}+\left(-8 z^{4}\right)-\left(-22 z^{2}\right) \\ &=-2 z^{5}-8 z^{4}+22 z^{2} \end{aligned} \nonumber$$

Альтернативне рішення:

Набагато ефективніше виконувати більшість кроків продукту$−2z^2(z^3 +4z^2 −11)$ подумки. Ми знаємо, що ми повинні$−2z^2$ множити на кожен з членів многочлена$z^3 +4z^2 −11$. Ось наші розумові розрахунки:

1. $−2z^2$раз$z^3$ дорівнює$−2z^5$.
2. $−2z^2$раз$4z^2$ дорівнює$−8z^4$.
3. $−2z^2$раз$−11$ дорівнює$22z^2$.

Мислення таким чином дозволяє нам записати відповідь без жодного з кроків, показаних у нашому першому рішенні. Тобто відразу пишемо:

$$-2 z^{2}\left(z^{3}+4 z^{2}-11\right)=-2 z^{5}-8 z^{4}+22 z^{2} \nonumber$$

Вправа$\PageIndex{7}$

Помножити:$-5 y^{3}\left(y^{2}-2 y+1\right)$

Відповідь

$-5 y^{5}+10 y^{4}-5 y^{3}$

Множення многочленів

Тепер, коли ми навчилися приймати добуток двох мономов або добуток монома і полінома, ми можемо застосувати те, що ми навчилися множити два довільних поліноми.

Перш ніж ми почнемо з прикладів, давайте переглянемо розподільну властивість. Ми знаємо, що $$2 \cdot(3+4)=2 \cdot 3+2 \cdot 4 \nonumber$$ обидві сторони рівні$14$. Ми звикли мати мономіальний фактор ліворуч, але він також може відображатися праворуч. $$(3+4) \cdot 2=3 \cdot 2+4 \cdot 2 \nonumber$$ Знову обидві сторони рівні$14$. Отже, чи з'являється мономіал зліва чи справа, не має різниці; тобто$a(b + c)=ab + ac$ і$(b + c)a = ba + ca$ дають той же результат. У кожному конкретному випадку ви$a$ множите на обидва члени$b + c$.

Приклад$\PageIndex{8}$

Помножити:$(2x + 5)(3x + 2)$

Рішення

Зверніть увагу, що$(2x + 5)(3x + 2)$ має вигляд$(b + c)a$, де$a$ знаходиться біном$3x+2$. Тому що$(b+c){\color {Red}a} = b{\color {Red}a}+c{\color {Red}a}$, ми будемо$3x+2$ множити на обидва$2x + 5$ члени наступним чином.

$$(2x + 5){\color {Red}(3x + 2)}=2x{\color {Red}(3x + 2)}+5{\color {Red}(3x + 2)} \nonumber$$

Тепер ми розподіляємо мономи раз многочлени, потім об'єднуємо як члени.

$$\begin{array}{l}{=6 x^{2}+4 x+15 x+10} \\ {=6 x^{2}+19 x+10}\end{array} \nonumber$$

Таким чином,$(2 x+5)(3 x+2)=6 x^{2}+19 x+10$

Вправа$\PageIndex{8}$

Помножити:$(3x + 4)(5x + 1)$

Відповідь

$15 x^{2}+23 x+4$

Приклад$\PageIndex{9}$

Помножити:$(x+5)\left(x^{2}+2 x+7\right)$

Рішення

Зверніть увагу, що$(x+5)(x^2 +2x+7)$ має вигляд$(b+c)a$, де$a$ знаходиться тріноміал$x^2 +2x+7$. Тому що$(b+c){\color {Red}a} = b{\color {Red}a}+c{\color {Red}a}$, ми будемо$x^2 +2x+7$ множити на обидва$x + 5$ члени наступним чином.

$$(x+5){\color {Red}\left(x^{2}+2 x+7\right)}=x{\color {Red}\left(x^{2}+2 x+7\right)}+5{\color {Red}\left(x^{2}+2 x+7\right)} \nonumber$$

Тепер ми розподіляємо мономи раз многочлени, потім об'єднуємо як члени.

$$\begin{array}{l}{=x^{3}+2 x^{2}+7 x+5 x^{2}+10 x+35} \\ {=x^{3}+7 x^{2}+17 x+35}\end{array} \nonumber$$

Таким чином,$(x+5)\left(x^{2}+2 x+7\right)=x^{3}+7 x^{2}+17 x+35$

Вправа$\PageIndex{9}$

Помножити:$(z+4)\left(z^{2}+3 z+9\right)$

Відповідь

$z^{3}+7 z^{2}+21 z+36$

Прискорення речей трохи

Давайте повторно розглянемо Приклад$\PageIndex{9}$ з надією розкрити візерунок, який дозволить множенню многочленів швидше протікати з меншою роботою. Зверніть увагу на перший крок Приклад$\PageIndex{9}$.

$$(x+5){\color {Red}\left(x^{2}+2 x+7\right)}=x{\color {Red}\left(x^{2}+2 x+7\right)}+5{\color {Red}\left(x^{2}+2 x+7\right)} \nonumber$$

Зверніть увагу, що перший продукт праворуч є результатом прийому продукту першого терміну$x + 5$ і$x^2 +2x + 7$. Аналогічно, другий твір праворуч є результатом взяття добутку другого терміну$x + 5$ і$x^2 +2x + 7$. Далі розберемо результат другого кроку.

$$(x+5)\left(x^{2}+2 x+7\right)=x^{3}+2 x^{2}+7 x+5 x^{2}+10 x+35 \nonumber$$

Перші три члени праворуч є результатом множення$x$ разів$x^2+2x+7$.

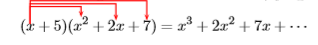
Другий набір з трьох членів праворуч є результатом множення$5$ разів$x^2 +2x + 7$.

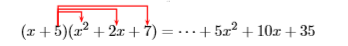
Ці примітки пропонують ефективний ярлик. Щоб помножити$x+5$ раз$x^2 +2x+7$,

• $x$Помножте на кожен член$x^2 +2x + 7$.
• $5$Помножте на кожен член$x^2 +2x + 7$.
• Поєднуйте подібні терміни.

Цей процес мав би наступний вигляд.

$$\begin{aligned}(x+5)\left(x^{2}+2 x+7\right) &=x^{3}+2 x^{2}+7 x+5 x^{2}+10 x+35 \\ &=x^{3}+7 x^{2}+17 x+35 \end{aligned} \nonumber$$

Приклад$\PageIndex{10}$

Скористайтеся описаною вище технікою ярликів для спрощення:$(2 y-6)\left(3 y^{2}+4 y+11\right)$

Рішення

$2y$Помножте на кожен член$3y^2 +4 y + 11$, а потім$−6$ помножте на кожен член$3y^2 +4y + 11$. Нарешті, комбінуйте подібні терміни.

$$\begin{aligned}(2 y-6)\left(3 y^{2}+4 y+11\right) &=6 y^{3}+8 y^{2}+22 y-18 y^{2}-24 y-66 \\ &=6 y^{3}-10 y^{2}-2 y-66 \end{aligned} \nonumber$$

Вправа$\PageIndex{10}$

Помножити:$(3 x+2)\left(4 x^{2}-x+10\right)$

Відповідь

$12 x^{3}+5 x^{2}+28 x+20$

Приклад$\PageIndex{11}$

Скористайтеся технікою швидкого доступу для спрощення$(a+b)^{2}$

Рішення

Для спрощення$(a+b)^2$ спочатку треба написати$a+b$ як коефіцієнт два рази.

$$(a+b)^{2}=(a+b)(a+b) \nonumber$$

Далі помножте на обидва члени$a + b$, помножте b раз обидва члени$a + b$, потім об'єднайте як члени.

$$\begin{array}{l}{=a^{2}+a b+b a+b^{2}} \\ {=a^{2}+2 a b+b^{2}}\end{array} \nonumber$$

Зверніть увагу, що$ab = ba$ оскільки множення є комутативним, так$ab + ba =2ab$.

Вправа$\PageIndex{11}$

Помножити:$(3 y-2)^{2}$

Відповідь

$9 y^{2}-12 y+4$

Приклад$\PageIndex{12}$

Скористайтеся технікою швидкого доступу, щоб спростити:$\left(x^{2}+x+1\right)\left(x^{2}-x-1\right)$

Рішення

Цього разу перший множник містить три члени$x^2$$x$$1$, і, тому ми спочатку множимо$x^2$ раз кожен член$x^2 −x−1$, потім$x$ раз кожен член$x^2 −x−1$, і$1$ раз кожен член$x^2 −x−1$. Потім ми поєднуємо подібні терміни.

$$\begin{aligned}\left(x^{2}+x+1\right)\left(x^{2}-x-1\right) &=x^{4}-x^{3}-x^{2}+x^{3}-x^{2}-x+x^{2}-x-1 \\ &=x^{4}-x^{2}-2 x-1 \end{aligned} \nonumber$$

Вправа$\PageIndex{12}$

Помножити:$\left(a^{2}-2 a+3\right)\left(a^{2}+2 a-3\right)$

Відповідь

$a^{4}-4 a^{2}+12 a-9$

Деякі програми

Нагадаємо, що площа окружності радіуса$r$ знаходять за формулою$A = πr^2$. Окружність (відстань навколо) окружності радіуса$r$ знаходять за формулою$C =2πr$ (див. Малюнок$\PageIndex{1}$).

Малюнок$\PageIndex{1}$: Формули для площі та окружності радіуса кола$r$.

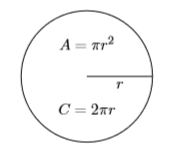
Приклад$\PageIndex{13}$

На малюнку$\PageIndex{2}$ зображені два концентричних кола (один і той же центр). Внутрішнє коло має радіус,$x$ а зовнішнє - радіус$x + 1$. Знайдіть площу затіненої області (званої кільцевим кільцем) як функцію$x$.

Малюнок$\PageIndex{2}$: Знайдіть площу затіненої області.

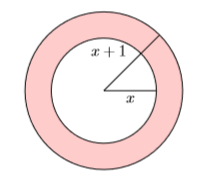
Рішення

Ми можемо знайти площу затіненої області, віднімаючи площу внутрішнього кола з області зовнішнього кола.

$$A=\text { Area of outer circle - Area of inner circle} \nonumber$$

Використовуємо$A = πr^2$ формулу для обчислення площі кожного кола. Оскільки зовнішнє коло має радіус$x+1$, він має площу$π(x+1)^2$. Оскільки внутрішнє коло має радіус$x$, воно має площу$πx^2$.

$$=\pi(x+1)^{2}-\pi x^{2} \nonumber$$

Далі ми розгорнемо$(x + 1)^2$, а потім об'єднаємо подібні терміни.

$$\begin{array}{l}{=\pi(x+1)(x+1)-\pi x^{2}} \\ {=\pi\left(x^{2}+x+x+1\right)-\pi x^{2}} \\ {=\pi\left(x^{2}+2 x+1\right)-\pi x^{2}}\end{array} \nonumber$$

Нарешті, розподіліть$π$ раз кожен термін$x^2 +2x + 1$, а потім об'єднайте як терміни.

$$\begin{array}{l}{=\pi x^{2}+2 \pi x+\pi-\pi x^{2}} \\ {=2 \pi x+\pi}\end{array} \nonumber$$

Значить, площа затіненої області є$A =2πx+ π$.

Вправа$\PageIndex{13}$

Дві концентричні кола показані нижче. Внутрішнє коло має радіус$x$ and the outer circle has radius $x + 2$. Find the area of the shaded region as a function of $x$.

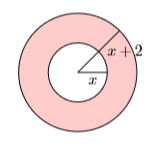
Відповідь

$4 \pi x+4 \pi$

Example $\PageIndex{14}$

The demand for widgets is a function of the unit price, where the demand is the number of widgets the public will buy and the unit price is the amount charged for a single widget. Suppose that the demand is given by the function $x = 270−0.75p$, where $x$ is the demand and $p$ is the unit price. Note how the demand decreases as the unit price goes up (makes sense). Use the graphing calculator to determine the unit price a retailer should charge for widgets so that his revenue from sales equals $\$20,000$.

Solution

To determine the revenue $(R)$, you multiply the number of widgets sold $(x)$ by the unit price $(p)$.

$$R=xp \label {Eq5.6.1}$$

However, we know that the number of units sold is the demand, given by the formula

$$x = 270−0.75p \label {Eq5.6.2}$$

Substitute equation $\ref {Eq5.6.2}$ into equation $\ref {Eq5.6.1}$ to obtain the revenue as a function of the unit price.

$$R = (270−0.75p)p \nonumber$$

Expand.

$$R=270 p-0.75 p^{2} \label {Eq5.6.3}$$

We’re asked to determine the unit price that brings in a revenue of $\$20,000$. Substitute $\$20,000$ for $R$ in equation $\ref {Eq5.6.3}$.

$$20000=270 p-0.75 p^{2} \label {Eq5.6.4}$$

Enter each side of equation $\ref {Eq5.6.4}$ into the Y= menu of your calculator (see the first image in Figure $\PageIndex{3}$). After some experimentation, we settled on the WINDOW parameters shown in the second image of Figure $\PageIndex{3}$. After making these settings, push the GRAPH button to produce the graph shown in the third image in Figure $\PageIndex{3}$.

Figure $\PageIndex{3}$: Solving $20000 = 270p−0.75p^2$.

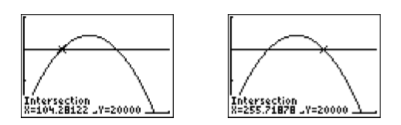
Note that the third image in Figure $\PageIndex{3}$ shows that there are two solutions, that is, two ways we can set the unit price to obtain a revenue of $\$20,000$. To find the first solution, select 5:intersect from the CALC menu, press ENTER in response to “First curve,” press ENTER in response to “Second curve,” then move your cursor closer to the point of intersection on the left and press ENTER in response to “Guess.” The result is shown in the first image in Figure $\PageIndex{4}$.

Repeat the process to find the second point of intersection. The result is shown in the second image in Figure $\PageIndex{4}$.

Figure $\PageIndex{4}$: Finding the points of intersection.

Note

In this example, the horizontal axis is actually the $p$-axis. So when we set $\mathrm{Xmin}$ and $\mathrm{Xmax}$, we’re actually setting bounds on the $p$-axis.

Reporting the solution on your homework:

Figure $\PageIndex{5}$: Reporting your graphical solution on your homework.

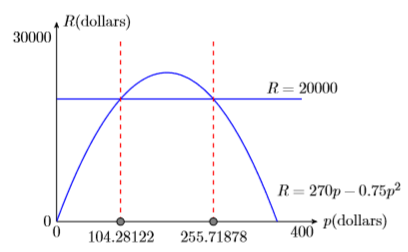
Duplicate the image in your calculator’s viewing window on your homework page. Use a ruler to draw all lines, but freehand any curves.

• Label the horizontal and vertical axes with $p$ and $R$, respectively (see Figure $\PageIndex{5}$). Include the units (dollars and dollars).
• Place your WINDOW parameters at the end of each axis (see Figure $\PageIndex{5}$).
• Label each graph with its equation (see Figure $\PageIndex{5}$).
• Drop a dashed vertical line through each point of intersection. Shade and label the $p$-values of the points where the dashed vertical lines cross the $p$-axis. These are the solutions of the equation $20000 = 270p− 0.75p^2$ (see Figure $\PageIndex{5}$).

Rounding to the nearest penny, setting the unit price at either $\$104.28$ or $\$255.72$ will bring in a revenue of $\$20,000$.

Exercise $\PageIndex{14}$

Suppose that the demand for gadgets is given by the function $x = 320−1.5p$, where $x$ is the demand and $p$ is the unit price. Use the graphing calculator to determine the unit price a retailer should charge for gadgets so that her revenue from sales equals $\$12,000$.

Answer

$\$ 48.55$ or $\$ 164.79$