5.7: Спеціальні продукти

Цей розділ присвячений поясненню ряду важливих ярликів для множення біноміалів. Це надзвичайно важливі шаблони, які дозволять виробляти ті ж продукти, обчислені в попередніх розділах. Важливо, щоб читачі практикували, поки вони не стануть ефективними, використовуючи кожен із шаблонів, представлених у цьому розділі.

Метод ФОЛЬГИ

Розглянемо добуток двох біноміалів$(x + 3)(x + 6)$. Ми вже знаємо, як знайти добуток цих двох двочленів; ми$x$ множимо на обидва члени$x + 6$, потім$3$ множимо на обидва члени$x + 6$.

$$(x+3)(x+6)=x^{2}+6 x+3 x+18 \nonumber$$

Зазвичай ми поєднуємо подібні терміни, але ми зупиняємо процес на цьому етапі, щоб ввести шаблон, який називається методом FOIL. Букви в слові FOIL означають «Перший», «Зовнішній», «Внутрішній» та «Останній».

Давайте подивимося, як ми можемо підключити ці умови до продукту$(x+3)(x+6)$.

• Стрілки вказують терміни в позиціях «Перший» в кожному біноміале. Якщо помножити члени в позиції «Перший», то вийде$x^2$. $${\color {Red}\underbrace{\color {Black}(x+3)(x}_{F}}+6) \nonumber$$
• Стрілки вказують терміни в позиціях «Зовнішній» в кожному біноміале. Якщо помножити члени в «Зовнішніх» позиціях, то вийде$6x$. $${\color {Red}\underbrace {\color {Black}(x+3)(x+6}_{O}}) \nonumber$$
• Стрілки вказують терміни в «Внутрішніх» положеннях в кожному біноміале. Якщо помножити члени в «Внутрішніх» позиціях, то вийде$3x$. $$(x+{\color {Red}\underbrace{\color {Black}{3)(x}}_{I}}+6) \nonumber$$
• Стрілки вказують терміни в позиціях «Останній» в кожному біноміале. Якщо помножити члени в позиціях «Останній», то вийде$18$. $$(x+{\color {Red}\underbrace{\color {Black}{3)(x+6}}_{L}}) \nonumber$$

Наступна діаграма показує зв'язок між «Перший», «Зовнішній», «Внутрішній», «Останній» та відповіддю.

$$(x+3)(x+6)=\begin{array}{ccccccc} \color {Red}{F} & {} & \color {Red}{O} & {} & \color {Red}{I} & {} & \color {Red}{L}\\ x^{2}&+&6x&+&3x&+&18\end{array} \nonumber$$

Приклад$\PageIndex{1}$

Скористайтеся методом FOIL, щоб спростити:$(x + 5)(x + 7)$

Рішення

Помножте позиції «Перші»:$x^2$. Помножте «Зовнішні» позиції:$7x$. Помножте «Внутрішні» позиції:$5x$. Помножте позиції «Останні»:$35$.

$$(x+5)(x+7)=\begin{array}{ccccccc} \color {Red}{F} & {} & \color {Red}{O} & {} & \color {Red}{I} & {} & \color {Red}{L}\\ x^{2}&+&7x&+&5x&+&35\end{array} \nonumber$$

Поєднуючи подібні терміни,$(x+5)(x+7)=x^{2}+12 x+35$

Вправа$\PageIndex{1}$

Спростити:$(x + 2)(x + 11)$

Відповідь

$x^{2}+13 x+22$

Приклад$\PageIndex{2}$

Скористайтеся методом FOIL, щоб спростити:$(2x−7)(x−4)$

Рішення

Помножте позиції «Перші»:$2x^2$. Помножте «Зовнішні» позиції:$−8x$. Помножте «Внутрішні» позиції:$−7x$. Помножте позиції «Останні»:$28$.

$$(2x-7)(x-4)=\begin{array}{ccccccc} \color {Red}{F} & {} & \color {Red}{O} & {} & \color {Red}{I} & {} & \color {Red}{L}\\ 2x^{2}&-&8x&-&7x&+&28\end{array} \nonumber$$

Поєднуючи подібні терміни,$(2 x-7)(x-4)=2 x^{2}-15 x+28$

Вправа$\PageIndex{2}$

Спростити:$(x−1)(4x + 5)$

Відповідь

$4 x^{2}+x-5$

На перший погляд, метод FOIL не схожий на значну частину ярлика. Адже якщо ми просто використовуємо дистрибутивне властивість на добутку Example$\PageIndex{2}$, то отримаємо такий же швидкий результат.

$$\begin{aligned}(2 x-7)(x-4) &=2 x(x-4)-7(x-4) \\ &=2 x^{2}-8 x-7 x+28 \\ &=2 x^{2}-15 x+28 \end{aligned} \nonumber$$

Метод FOIL стає справжнім ярликом, коли ми додаємо результати «Outer» та «Inner» у нашій голові.

Фольга Ярлик

Щоб помножити два біноміали, виконайте наступні дії:

1. Помножте члени в позиціях «Перші».
2. Помножте члени в положеннях «Зовнішнє» і «Внутрішнє» і об'єднайте результати подумки (якщо вони схожі на терміни).
3. Помножте члени в позиціях «Останній».

Приклад$\PageIndex{3}$

Скористайтеся ярликом FOIL, щоб спростити:$(3x + 8)(2x−1)$

Рішення

Кожен з наступних етапів виконується подумки.

1. Помножте члени в позиціях «Перші»:$6x^2$
2. Помножте члени в положеннях «Зовнішнє» і «Внутрішнє» і додайте результати подумки:$−3x + 16x = 13x$
3. Помножте значення в позиціях «Останній»:$−8$

Напишіть відповідь без проміжних кроків:$(3 x+8)(2 x-1)=6 x^{2}+13 x-8$

Вправа$\PageIndex{3}$

Спростити:$(2z−3)(5z−1)$

Відповідь

$10 z^{2}-17 z+3$

Приклад$\PageIndex{4}$

Скористайтеся ярликом FOIL, щоб спростити:$(4y−3)(5y + 2)$

Рішення

Кожен з наступних етапів виконується подумки.

1. Помножте члени в позиціях «Перші»:$20y^2$
2. Помножте члени в положеннях «Зовнішнє» і «Внутрішнє» і додайте результати подумки:$8y−15y = −7y$
3. Помножте значення в позиціях «Останній»:$−6$

Напишіть відповідь без проміжних кроків:$(4 y-3)(5 y+2)=20 y^{2}-7 y-6$

Вправа$\PageIndex{4}$

Спростити:$(7 x+2)(2 x-3)$

Відповідь

$14 x^{2}-17 x-6$

Різниця квадратів

Ми можемо використовувати ярлик FOIL для множення$(a + b)(a−b)$.

1. Помножте члени в позиціях «Перші»:$a^2$
2. Помножте члени в положеннях «Зовнішнє» і «Внутрішнє» і додайте результати подумки:$ab−ab =0$
3. Помножте значення в позиціях «Останній»:$−b^2$

Таким чином,$(a+b)(a-b)=a^{2}-b^{2}$. Зверніть увагу, як права сторона$a^2 −b^2$ - це різниця двох квадратів. Це призводить до наступного ярлика.

Різниця квадратів

Якщо у вас є однакові терміни в позиціях «Перший» і ідентичні члени в позиціях «Останній», але один набір відокремлений знаком плюс, а інший розділений знаком мінус, то дійте наступним чином:

1. Квадратний термін «Перший».
2. Квадратний термін «Останній».
3. Помістіть знак мінус між результатами

Тобто,

$$(a+b)(a-b)=a^{2}-b^{2} \nonumber$$

Примітка

Якщо у вас немає однакових термінів у позиціях «Перший» та «Останній», один набір розділений знаком плюс, а інший зі знаком мінус, то у вас немає різниці квадратів, і ви повинні знайти інший спосіб множення. Наприклад,$(x+3)(x−3)$ є прикладом відмінності квадратів візерунком, але не$(2y + 3)(2y−5)$ є.

Приклад$\PageIndex{5}$

Скористайтеся клавіатурним скороченням різниці квадратів, щоб спростити:$(x+3)(x− 3)$

Рішення

Зверніть увагу, як терміни в позиції «Перший» ідентичні, як і терміни в позиції «Останній», причому один набір розділений знаком плюс, а інший зі знаком мінус. Отже, це різниця квадратів візерунка і ми чинимо наступним чином:

1. Квадратний термін у позиції «Перший»:$x^2$
2. Квадратний термін у позиції «Останній»:$(−3)^2 =9$
3. Розділіть квадрати зі знаком мінус.

Тобто:

$$\begin{aligned}(x+3)(x-3) &=x^{2}-(3)^{2} \\ &=x^{2}-9 \end{aligned} \nonumber$$

Примітка

Ви повинні практикувати цю схему, поки ви не зможете перейти прямо від постановки завдання до відповіді, не записуючи жодної проміжної роботи, як в$(x + 3)(x−3) = x^2 −9$.

Вправа$\PageIndex{5}$

Спростити:$(x + 5)(x−5)$

Відповідь

$x^{2}-25$

Приклад$\PageIndex{6}$

Скористайтеся клавіатурним скороченням різниці квадратів, щоб спростити:$(8y +7z)(8y−7z)$

Рішення

Зверніть увагу, як терміни в позиції «Перший» ідентичні, як і терміни в позиції «Останній», причому один набір розділений знаком плюс, а інший зі знаком мінус. Отже, це різниця квадратів візерунка і ми чинимо наступним чином:

1. Квадратний термін у позиції «Перший»:$(8y)^2 = 64 y^2$
2. Квадратний термін у позиції «Останній»:$(7z)^2 = 49 z^2$
3. Розділіть квадрати зі знаком мінус.

Тобто:

$$\begin{aligned}(8 y+7 z)(8 y-7 z) &=(8 y)^{2}-(7 z)^{2} \\ &=64 y^{2}-49 z^{2} \end{aligned} \nonumber$$

Примітка

Ви повинні практикувати цю схему до тих пір, поки ви не зможете перейти прямо від постановки завдання до відповіді, не записуючи жодної проміжної роботи, як в$(8 y+7 z)(8 y-7 z)=64 y^{2}-49 z^{2}$

Вправа$\PageIndex{6}$

Спростити:$(3a−6b)(3a +6b)$

Відповідь

$9 a^{2}-36 b^{2}$

Приклад$\PageIndex{7}$

Скористайтеся клавіатурним скороченням різниці квадратів, щоб спростити:$\left(x^{3}-5 y^{2}\right)\left(x^{3}+5 y^{2}\right)$

Рішення

Зверніть увагу, як терміни в позиції «Перший» ідентичні, як і терміни в позиції «Останній», причому один набір розділений знаком плюс, а інший зі знаком мінус. Отже, це різниця квадратів візерунка і ми чинимо наступним чином:

1. Квадратний термін у позиції «Перший»:$(x^3)^2 = x^6$
2. Квадратний термін у позиції «Останній»:$(5y^2)^2 = 25 y^4$
3. Розділіть квадрати зі знаком мінус.

Тобто:

$$\begin{aligned}\left(x^{3}-5 y^{2}\right)\left(x^{3}+5 y^{2}\right) &=\left(x^{3}\right)^{2}-\left(5 y^{2}\right)^{2} \\ &=x^{6}-25 y^{4} \end{aligned} \nonumber$$

Примітка

Ви повинні практикувати цю схему до тих пір, поки ви не зможете перейти прямо від постановки завдання до відповіді, не записуючи жодної проміжної роботи, як в$\left(x^{3}-5 y^{2}\right)\left(x^{3}+5 y^{2}\right)=x^{6}-25 y^{4}$

Вправа$\PageIndex{7}$

Спростити:$\left(2 y^{4}+z^{3}\right)\left(2 y^{4}-z^{3}\right)$

Відповідь

$4 y^{8}-z^{6}$

Квадратне біноміальне

Перш ніж продемонструвати правильну процедуру квадратування бінома, ми спочатку поділимося однією з найпоширеніших помилок, допущених в алгебрі.

Попередження! Це неправильно!

Однією з найпоширеніших помилок, допущених в алгебрі, є припущення, що:

$$(a+b)^{2}=a^{2}+b^{2} \nonumber$$

Те, що це неправильно, легко перевіряється. Замінник$a$ і$3$$4$ для$b$.

$$\begin{aligned}(3+4)^{2} &=3^{2}+4^{2} \\ 7^{2} &=3^{2}+4^{2} \\ 49 &=9+16 \end{aligned} \nonumber$$

Ясно, що це неправильно!

Так що ж таке правильна відповідь? По-перше,$(a+b)^{2}=(a+b)(a+b)$. Тепер ми можемо використовувати ярлик FOIL.

1. Помножте члени в позиціях «Перші»:$a^2$
2. Помножте члени в положеннях «Зовнішнє» і «Внутрішнє» і додайте результати подумки:$ab + ab =2ab$
3. Помножте значення в позиціях «Останній»:$b^2$

Отже, правильна відповідь є$(a+b)^{2}=a^{2}+2 a b+b^{2}$. Це призводить нас до наступного ярлика для квадратування біноміального.

Квадратування біноміального

Щоб зробити квадрат біном, наприклад$(a + b)^2$, виконайте наступні дії:

1. Квадратний термін «Перший»:$a^2$
2. Помножте «Перший» і «Останній» терміни і подвоюйте результат:$2ab$
3. Квадратний термін «Останній»:$b^2$

Тобто:

$$(a+b)^{2}=a^{2}+2 a b+b^{2} \nonumber$$

Приклад$\PageIndex{8}$

Скористайтеся квадратом біноміального клавіатурного скорочення, щоб розгорнути:$(x+5)^{2}$

Рішення

Виконайте наступні дії:

1. Квадратний перший термін:$x^2$
2. Помножте «Перший» і «Останній» терміни і подвоюйте результат:$2(x)(5) = 10x$
3. Квадратний термін «Останній»:$5^2 = 25$

Таким чином:

$$\begin{aligned}(x+5)^{2} &=x^{2}+2(x)(5)+(5)^{2} \\ &=x^{2}+10 x+25 \end{aligned} \nonumber$$

Примітка

Ви повинні практикувати цю схему до тих пір, поки ви не зможете перейти прямо від постановки завдання до відповіді, не записуючи жодної проміжної роботи, як в$(x+5)^{2}=x^{2}+10 x+25$

Вправа$\PageIndex{8}$

Спростити:$(x+3)^{2}$

Відповідь

$x^{2}+6 x+9$

Коментар

Студенти часто відмовляються вивчати ярлик «квадрат біноміального», відзначаючи, що вони можуть так само легко використовувати техніку FOIL або просте застосування розподільної властивості, щоб досягти того ж результату. На жаль, нездатність вивчити ярлик «квадрат біноміального» буде серйозно перешкоджати студентам, оскільки ця закономірність є важливою складовою багатьох процедур у майбутніх курсах математики.

Приклад$\PageIndex{9}$

Скористайтеся квадратом біноміального клавіатурного скорочення, щоб розгорнути:$(3 x+7 y)^{2}$

Рішення

Виконайте наступні дії:

1. Квадратний перший термін:$(3x)^2 =9x^2$
2. Помножте «Перший» і «Останній» терміни і подвоюйте результат:$2(3x)(7y)= 42xy$
3. Квадратний термін «Останній»:$(7y)^2 = 49 y^2$

Таким чином:

$$\begin{aligned}(3 x+7 y)^{2} &=(3 x)^{2}+2(3 x)(7 y)+(7 y)^{2} \\ &=9 x^{2}+42 x y+49 y^{2} \end{aligned} \nonumber$$

Примітка

Ви повинні практикувати цю схему до тих пір, поки ви не зможете перейти прямо від постановки завдання до відповіді, не записуючи жодної проміжної роботи, як в$(3 x+7 y)^{2}=9 x^{2}+42 x y+49 y^{2}$

Вправа$\PageIndex{9}$

Спростити:$(2 y+3 z)^{2}$

Відповідь

$4 y^{2}+12 y z+9 z^{2}$

У наступному прикладі при квадратиці двочлена зі знаком мінус подбаємо про знак мінус «додаючи протилежне».

Приклад$\PageIndex{10}$

Скористайтеся квадратом біноміального клавіатурного скорочення, щоб розгорнути:$\left(4 a^{2}-5 b^{3}\right)^{2}$

Рішення

Додайте протилежне:$(4a^2−5b^3)^2 = (4 a^2+(−5b^3))^2$. Тепер виконайте наступні дії:

1. Квадратний перший термін:$(4a^2)^2 = 16 a^4$
2. Помножте «Перший» і «Останній» терміни і подвоюйте результат:$2(4a^2)(−5b^3)= −40a^2b^3$
3. Квадратний термін «Останній»:$(−5b^3)^2 = 25 b^6$

Таким чином:

$$\begin{aligned}\left(4 a^{2}-5 b^{3}\right)^{2} &=\left(4 a^{2}+\left(-5 b^{3}\right)\right)^{2} \\ &=\left(4 a^{2}\right)^{2}+2\left(4 a^{2}\right)\left(-5 b^{3}\right)+\left(-5 b^{3}\right)^{2} \\ &=16 a^{4}-40 a^{2} b^{3}+25 b^{6} \end{aligned} \nonumber$$

Примітка

Ви повинні практикувати цю схему до тих пір, поки ви не зможете перейти прямо від постановки завдання до відповіді, не записуючи жодної проміжної роботи, як в

$$\left(4 a^{2}-5 b^{3}\right)^{2}=16 a^{4}-40 a^{2} b^{3}+25 b^{6} \nonumber$$

Вправа$\PageIndex{10}$

Спростити:$\left(3 x^{4}-5 z^{2}\right)^{2}$

Відповідь

$9 x^{8}-30 x^{4} z^{2}+25 z^{4}$

Приклад$\PageIndex{10}$ показує нам, що якщо ми беремо різницю в квадраті, середній термін буде мінус. Тобто єдина відмінність між$(a+b)^2$ і$(a−b)^2$ є ознакою середнього терміну.

Квадратування біноміального

Комбінації клавіш для зведення бінома в квадрат:

$$(a+b)^{2}=a^{2}+2 a b+b^{2} \nonumber$$

$$(a-b)^{2}=a^{2}-2 a b+b^{2} \nonumber$$

Приклад$\PageIndex{11}$

Скористайтеся квадратом біноміального клавіатурного скорочення, щоб розгорнути:$\left(x^{3}-y^{3}\right)^{2}$

Рішення

Використовуйте викрійку$(a−b)^2 = a^2 −2ab+ b^2$. Квадратний «Перший» член, помножте «Перший» і «Останній» члени і подвоїти результат, а потім квадрат «Останній» термін. Через знака мінус середнім терміном буде мінус, а ось всі інші терміни - плюс.

$$\begin{aligned}\left(x^{3}-y^{3}\right)^{2} &=\left(x^{3}\right)^{2}-2\left(x^{3}\right)\left(y^{3}\right)+\left(y^{3}\right)^{2} \\ &=x^{6}-2 x^{3} y^{3}+y^{6} \end{aligned} \nonumber$$

Вправа$\PageIndex{11}$

Спростити:$\left(a^{2}-3 b^{5}\right)^{2}$

Відповідь

$a^{4}-6 a^{2} b^{5}+9 b^{10}$

Додаток

У прикладі$\PageIndex{7}$ ми знайшли площу зовнішнього квадрата шляхом підсумовування площ його частин (див. Рис.$\PageIndex{1}$). Нагадаємо, що відповідь була$A = x^2 + 6x + 9$.

Малюнок$\PageIndex{1}$: Знайдіть площу квадрата.

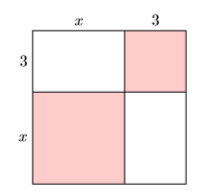
Тепер, коли у нас є квадрат біноміального ярлика, ми можемо спростити процес знаходження площі зовнішнього квадрата шляхом квадратизації його сторони. Тобто:

$$A=(x+3)^{2} \nonumber$$

Тепер ми можемо використовувати квадратичну біноміальну техніку для розширення.

$$\begin{array}{l}{=x^{2}+2(x)(3)+(3)^{2}} \\ {=x^{2}+6 x+9}\end{array} \nonumber$$

Зауважте, що це те саме, що і відповідь, знайдена шляхом підсумовування чотирьох частин квадрата в прикладі$\PageIndex{7}$.