5.1: Функції

Last updated
Save as PDF

Page ID: 58281

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Почнемо з визначення відношення.

Відносини

Відношення - це сукупність впорядкованих пар.

Збірка впорядкованих пар\[R =\{(0,3),(0,4),(1,5),(2,6)\} \nonumber \] є прикладом відношення.

Якщо ми збираємо перший елемент кожної впорядкованої пари в множині, ми маємо те, що називається доменом відношення.

Домен

Домен відношення - це множина всіх перших елементів впорядкованих пар.

Наприклад, у відношенні,\[R = \{(0,3),(0,4),(1,5),(2,6)\} \nonumber \] якщо ми збираємо перший елемент кожної впорядкованої пари$R$, ми отримуємо домен:\[\text {Domain of R} = \{0,1,2\} \nonumber \] Хоча число нуль з'являється двічі як перший елемент у впорядкованих парах, зауважте$R$, що ми перераховуємо його лише один раз при перерахуванні елементів у домені $R$.

Подібним чином, якщо ми збираємо другі елементи кожної впорядкованої пари в набір, ми маємо те, що називається діапазоном відношення.

Діапазон

Діапазон відношення - це множина всіх других елементів впорядкованих пар.

Наприклад, у співвідношенні,\[R = \{(0,3),(0,4),(1,5),(2,6)\} \nonumber \] якщо ми збираємо другий елемент кожної впорядкованої пари$R$, то отримаємо діапазон:\[\text {Range of R} = \{3,4,5,6\} \nonumber \]

Приклад$\PageIndex{1}$

Створіть домен і діапазон відношення\[T = \{(5,3),(6,3),(7,4)\} \nonumber \]

Рішення

Зберіть перший елемент кожної впорядкованої пари$T$ в список домену:

Домен$T=\{5,6,7\}$

Зберіть другий елемент кожної впорядкованої пари,$T$ щоб перелічити діапазон:

Асортимент$T=\{3,4\}$

Зверніть увагу, що хоча цифра три з'являється у другій позиції двічі, ми перерахуємо її лише один раз при описі діапазону.

Вправа$\PageIndex{1}$

Створіть домен і діапазон відношення\[S =\{(−1,7),(2,5),(2,3)\} \nonumber \]

Відповідь: Домен$S = \{−1,2\}$, Range of $S = \{3,5,7\}$

Приклад$\PageIndex{2}$

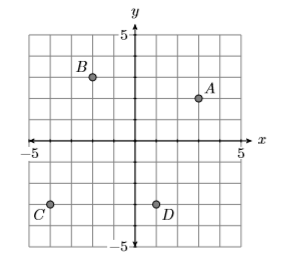
Створіть домен і діапазон відношення, показаного на малюнку$\PageIndex{1}$.

рис 5.1.1.png — Малюнок$\PageIndex{1}$: Ми можемо представити відношення як сукупність впорядкованих пар у графіку.

Рішення

Точка$A$ має координати$(3,2)$, точка$B$ має координати$(−2,3)$, точка$C$ має координати$(−4,−3)$, а точка$D$ має координати$(1,−3)$. Ми можемо зібрати ці очки в набір. \[S = \{(3,2),(−2,3),(−4,−3),(1,−3)\} \nonumber \]

Якщо ми збираємо кожен елемент у першій позиції кожної впорядкованої пари, ми маємо домен.

Домен$S = \{−4,−2,1,3\}$

Зверніть увагу, що традиційно перераховувати елементи домену по порядку (від найменшого до найбільшого). Далі, якщо ми збираємо кожен елемент у другій позиції кожної впорядкованої пари, у нас є діапазон.

Асортимент$S = \{−3,2,3\}$

Знову ж таки, традиційно перераховувати елементи по порядку. Зауважте ще раз, що ми не повторювали число$−3$ в перерахуванні діапазону, хоча він використовується двічі як другий елемент впорядкованої пари в наборі$S$.

Вправа$\PageIndex{2}$

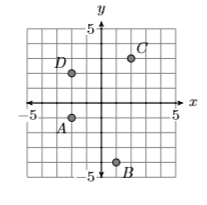
Вкажіть домен і діапазон відношення, показаного нижче.

$Ех 5.1.2.png$

Відповідь: Домен$S =\{−2,1,2\}$, Range of $S =\{−4,−1,2,3\}$

Картографічні діаграми

Діаграма відображення є корисною конструкцією, яка допомагає аналізувати зв'язок. Розглянемо більш$R =\{(0,3),(0,4),(1,5),(2,6)\}$ ранні відносини, які мали домен$\mathcal{D} = \{0,1,2\}$ і діапазон$\mathcal{R} = \{3,4,5,6\}$. Для побудови діаграми відображення для$R$, перерахуйте елементи в області зліва, перерахуйте елементи діапазону праворуч, потім за допомогою стрілок вказуйте впорядковані пари (див. Рис.$\PageIndex{2}$).$R$$R$

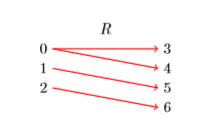
рис 5.1.2.png — Рисунок$\PageIndex{2}$: Використання діаграми відображення для опису відношення$R$.

Зверніть увагу, як$(0,3)$ позначається впорядкована пара, намалювавши стрілку, що$0$ з'єднується$3$ зліва до праворуч. Ми говоримо, що відношення «карти$0$ до$3$» і пишемо$R : 0 \rightarrow 3$. Подібним чином:

$(0,4)$Впорядкована пара позначається малюванням стрілки, що$0$ з'єднується$4$ зліва направо; тобто$R$ «карти$0$ до$4$» або$R :0→ 4$.
$(1,5)$Впорядкована пара позначається малюванням стрілки, що$1$ з'єднується$5$ зліва направо; тобто$R$ «карти$1$ до$5$» або$R :1→ 5$.
$(2,6)$Впорядкована пара позначається малюванням стрілки, що$2$ з'єднується$6$ зліва направо; тобто$R$ «карти$2$ до$6$» або$R :2→ 6$.

Приклад$\PageIndex{3}$

Створіть діаграму відображення для зв'язку в прикладі$\PageIndex{1}$.

Рішення

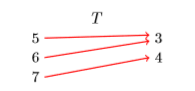
Відношення Приклад$\PageIndex{1}$ є$T=\{(5,3),(6,3),(7,4)\}$. Перерахуйте домен$\mathcal{D}=\{5,6,7\}$ зліва, діапазон$\mathcal{R}=\{3,4\}$ справа, потім за допомогою стрілок вказуйте впорядковані пари (див.$\PageIndex{3}$ Рис.

рис. 5.1.3.png — Малюнок$\PageIndex{3}$: Діаграма відображення для зв'язку$T$.

Визначення функції

Функція - це дуже особливий тип відношення.

Функція

Відношення - це функція тоді і лише тоді, коли кожен об'єкт у домені сполучено рівно з одним об'єктом у діапазоні.

В якості першого прикладу розглянемо відношення, діаграма відображення$R = \{(0,3),(0,4),(1,5),(2,6)\}$ якого зображена на малюнку$\PageIndex{2}$. Зверніть увагу, що$0$ в домені відбувається парне з'єднання з двома об'єктами$4$,$3$ причому, в діапазоні. Отже, відношення не$R$ є функцією.

В якості другого прикладу розглянемо відношення$T =\{(5,3),(6,3),(7,4)\}$, схема відображення якого зображена на малюнку$\PageIndex{3}$. У цьому прикладі кожен об'єкт домену поєднується рівно з одним об'єктом діапазону: надсилається$5$$6$ лише до$3$, надсилається лише до$3$ та надсилається$7$ лише до$4$. Значить, відношення$T$ є функцією. Той факт, що об'єкт діапазону$3$ використовується двічі, значення не має. Це той факт, що кожен об'єкт домену надсилається рівно до одного об'єкта діапазону, який має значення.

Приклад$\PageIndex{4}$

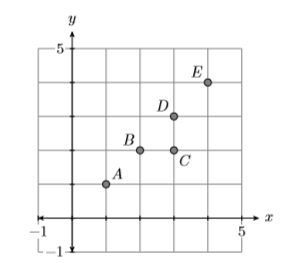
Розглянемо співвідношення, зображене на малюнку$\PageIndex{4}$. Це функція?

рис 5.1.4.png — Малюнок$\PageIndex{4}$: Чи є це відношення функцією?

Рішення

Графік на малюнку$\PageIndex{4}$ складається з точок$A(1,1)$,$B(2,2)$,$C(3,2)$,$D(3,3)$, і$E(4,4)$. Домен є$\mathcal{D}=\{1,2,3,4\}$ і діапазон є$\mathcal{R}=\{1,2,3,4\}$. Діаграма відображення (див. Рис.$\PageIndex{5}$) допоможе нам вирішити, чи є відношення, представлене графіком, функцією. Поставте домен зліва, діапазон праворуч, потім за допомогою стрілок вказуйте впорядковані пари. Назвемо відношення$f$.

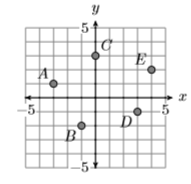
Ех 5.1.4.png — Рисунок$\PageIndex{5}$: Діаграма відображення співвідношення,$f$ зображеного на малюнку$\PageIndex{4}$.

На малюнку зверніть увагу$\PageIndex{5}$, як об'єкт домену «відправляється» або$3$ поєднується з двома об'єктами діапазону,$2$ і$3$. Значить, відношення не$f$ є функцією.

Вправа$\PageIndex{4}$

Розглянемо співвідношення, зображені нижче. Це функція?

$Ех 5.1.4.png$

Відповідь: Так, відношення - це функція.

Приклад$\PageIndex{5}$

Наступне співвідношення пари автомобілів з їх пробігом газу. Визначте, чи є відношення функцією.

\[T =\{\text {(Bentley Mulsanne,18),(Kia Soul,30),(Lamborghini Gallardo,20), (Smart Fortwo,41),(Jaguar XF,23)} \} \nonumber \]

Рішення

На малюнку$\PageIndex{6}$ створюємо картограмну діаграму із зазначенням співвідношення між автомобілями і їх пробігом газу. Зверніть увагу, що кожен об'єкт домену зліва поєднується з рівно одним об'єктом діапазону праворуч. Значить, це відношення є функцією.

рис 5.1.6.png — Малюнок$\PageIndex{6}$: Діаграма відображення для зв'язку$T$.

Вправа$\PageIndex{5}$

Наступне співвідношення пари людей з їх віком. Визначте, чи є відношення функцією.

\[S = \{\text {(Mary,23),(Joe,18), (Alfonzo,20),(Zoe,18), (Maria,22),(Chris,23) } \} \nonumber \]

Відповідь: Так, відношення - це функція.

Приклад$\PageIndex{6}$

Наступне співвідношення поєднує конкретну птицю з державою, яка прийняла цю птицю як її державний птах. Визначте, чи є відношення функцією.

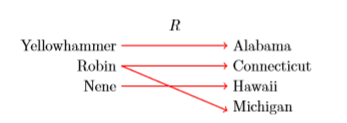
\[R=\{\text { (Yellowhammer, Alabama), (Robin, Connecticut), (Nene, Hawaii), (Robin, Michigan) } \} \nonumber \]

Рішення

На малюнку$\PageIndex{7}$ ми створюємо картографічну діаграму із зазначенням співвідношення між птахами та їх державними усиновленнями. Зверніть увагу, що об'єкт домену «Робін» поєднується з двома об'єктами діапазону, «Коннектикут» та «Мічиган», отже, це відношення не є функцією.

рис 5.1.7.png — Малюнок$\PageIndex{7}$: Діаграма відображення для зв'язку$R$.

Вправа$\PageIndex{6}$

Наступне співвідношення поєднує людей з типами автомобілів, якими вони володіють. Визначте, чи є відношення функцією.

\[S = \{\text {(Bernard,station wagon), (Tina,truck), (Gilberto,sedan), (Kate,sport utility), (Bernard,sedan), (Kate,minivan)} \} \nonumber \]

Відповідь: Ні, відношення не є функцією.

Позначення діаграми відображення

Метою цього розділу є введення позначення функцій. Почнемо з діаграми відображення на малюнку$\PageIndex{8}$.

рис 5.1.8.png — Малюнок$\PageIndex{8}$: Діаграма відображення.

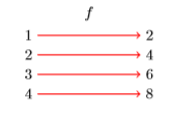
Діаграма відображення на малюнку$\PageIndex{8}$ виявляє наступні факти:

$f$карти$1$ до$2$ або$f :1→ 2$
$f$карти$2$ до$4$ або$f :2→ 4$
$f$карти$3$ до$6$ або$f :3→ 6$
$f$карти$4$ до$8$ або$f :4→ 8$

Зверніть увагу, як позначення добре$f :4→ 8$ корелює з діаграмою відображення на малюнку$\PageIndex{8}$. Позначення$f :4→ 8$ читається «$f$карти$4$ на$8$» або «$f$посилає$4$»$8$.

Більш уважний погляд на діаграму відображення на малюнку$\PageIndex{8}$ виявляє цікаву закономірність. «Правило», здається, полягає в тому, що відношення$f$ подвоює кожен запис у своєму домені: двічі$1$$3$ є$2$$6$, двічі є, двічі є і т.д. можна дати загальний опис цього «правила», написавши:\[f : x→ 2x (5.1) \label{Eq5.1.1} \] Тобто$f$ посилає$2$$4$ $x$в два рази$x$, або еквівалентно,$2x$. Наприклад, ми можемо запитати «куди$f$ надсилає$15$?» Щоб відповісти на це питання, ми б замінити$x$ з$15$ в правилі\ ref {Eq5.1.1}, щоб отримати\[f : 15→ 2(15) \nonumber \] або еквівалентно,\[f : 15→ 30 \nonumber \] Ми також могли б запитати «куди$f$ відправляти$−7$?» Щоб відповісти на це питання, ми б$x$ замінити на$−7$ в правилі\ ref {Eq5.1.1}, щоб отримати\[f : −7→ 2(−7) \nonumber \] або еквівалентно,\[f : −7 →−14 \nonumber \]

Приклад$\PageIndex{7}$

З огляду на правило$f : x → 2x + 3$, дайте відповідь на питання «куди$f$ відправляють$8$?»

Рішення

Щоб знайти, де «$f$посилає»$8$, замінити$8$$x$$f : x → 2x + 3$ в правилі отримати\[f :8→ 2(8) + 3 \nonumber \] або еквівалентно,\[f :8→ 19 \nonumber \]

Вправа$\PageIndex{7}$

З огляду на правило$f : x → 3x−5$, answer the question “where does $f$ send $−2$?”

Відповідь: $ f : −2 →−11$

Приклад$\PageIndex{8}$

З огляду на правило$f : x → x/(x+3)$, дайте відповідь на питання «куди$f$ відправляють$−1$?»

Рішення

Щоб знайти, де «$f$посилає»$−1$, замінити$−1$$x$$f : x→ x/(x + 3)$ в правилі отримати\[f :-1 \rightarrow \frac{-1}{-1+3} \nonumber \] або еквівалентно,\[f :-1 \rightarrow-\dfrac{1}{2} \nonumber \]

Вправа$\PageIndex{8}$

З огляду на правило$f : x → 2x^2 +5x$, answer the question “where does $f$ send $3$?”

Відповідь: $f : 3 \rightarrow 33$

У Прикладах$\PageIndex{7}$ і$\PageIndex{8}$, зауважте, що кожен раз, коли ви підставляєте значення для$x$ в даному правилі, ви отримуєте унікальну відповідь. Це означає, що кожен об'єкт в області$f$ надсилається унікальному об'єкту в діапазоні$f$, складаючи правила в Прикладах$\PageIndex{7}$ і$\PageIndex{8}$ функціях. Це призводить нас до деталізованого опису функції.

Правило трьох

Функція складається з трьох частин:

набір об'єктів, які математики називають доменом
другий набір об'єктів, які математики називають діапазоном
правило, яке описує, як призначити кожен об'єкт у домені рівно одному об'єкту в діапазоні.

Функція позначення

Хоча позначення діаграми відображення$f : x→ 3−4x$ досить легко зрозуміти, використовується стандартне позначення функції$f(x)=3−4x$. З відображенням позначення діаграми, якщо ми хочемо відповісти на питання «куди$f$ надсилає$12$?» , пишемо:

\[\begin{array}{c}{f : x \rightarrow 3-4 x} \\ {f : 12 \rightarrow 3-4(12)} \\ {f : 12 \rightarrow 3-48} \\ {f : 12 \rightarrow-45}\end{array} \nonumber \]

Отже,$f : 12→−45$; тобто$f$ посилає$12$ в$−45$. Функція позначення використовує точно таке ж поняття; тобто замінник$12$$x$.

Поради щодо використання позначення функцій

Замініть усі входження змінних у позначеннях відкритими дужками. Залиште місце між дужками, щоб підставити задане значення змінної.
Підставляємо задані значення змінних у відкриті дужки, підготовлені на першому кроці.
Оцінити отриманий вираз відповідно до Правил Керівного Порядку операцій.

Дано$f(x)=3−4x$, щоб оцінити$f(12)$, спочатку перевстановити позначення функції, а потім замінити кожне входження змінної відкритими дужками.

\[\begin{aligned} f(x)&= 3-4 x \quad \color {Red} \text { Original function notation. } \\ f(\; \; ) &= 3-4(\; \; ) \quad \color {Red} \text { Replace each occurrence of } x \text { with open parentheses. } \end{aligned} \nonumber \]

Тепер$12$ підставляємо$x$ в відкриті дужки, підготовлені на останньому кроці.

\[\begin{aligned} f({\color {Red} 12})&= 3-4({\color {Red} 12}) \quad \color {Red} \text { Substitute } 12 \text { for } x \text { in the open parentheses positions. } \\ f(12) &= 3-48 \quad \color {Red} \text { Multiply. } \\ f(12) &= -45 \quad \color {Red} \text { Subtract. } \end{aligned} \nonumber \]

Отже,$f(12) =−45$; тобто$f$ посилає$12$ в$−45$.

Приклад$\PageIndex{9}$

Дано$f(x)=4−5x−x^2$, оцініть$f(−3)$.

Рішення

Почніть з заміни кожного входження змінної$x$ відкритими дужками.

\[\begin{aligned} f(x) &=4-5 x-x^{2} \quad \color {Red} \text { Original function notation. }\\ f( & )=4-5(\quad)-(\quad)^{2} \quad \color {Red} \text { Replace each occurrence of } x \text { with open parentheses. } \end{aligned} \nonumber \]

Тепер$−3$ підставляємо$x$ в відкриті дужки, підготовлені на останньому кроці.

\[\begin{aligned} f({\color {Red}-3}) &= 4-5({\color {Red}-3})-({\color {Red}-3})^{2} \quad \color {Red} \text { Substitute }-3 \text { for } x \text { in the open parentheses positions. } \\ f(-3) &= 4-5(-3)-9 \quad \color {Red} \text { Evaluate exponent: }(-3)^{2}=9 \\ f(-3) &= 4+15-9 \quad \color {Red}\text { Multiply: }-5(-3)=15\\ f(-3) &= 10 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]

Таким чином,$f(−3) = 10$. Перевірте це на своєму калькуляторі (див. Малюнок$\PageIndex{9}$).

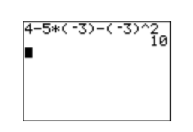
рис 5.1.9.png — Малюнок$\PageIndex{9}$: Перевірка калькулятора.

Наступний приклад демонструє одну з переваг позначення функцій. Наприклад, легко посилатися на функцію, в якій потрібно підставити задане$x$ -значення.

Приклад$\PageIndex{10}$

Дано$f(x)=5−x$ і$g(x)=x^2 −9$, знайдіть$f(−1)$ і$g(−2)$.

Рішення

Нам дано два визначення функції,$f$ і$g$, але ми спочатку попросили знайти$f(−1)$. Це означає, що ми повинні замінити кожне входження$x$ з$−1$ у функції$f(x)=5−x$.

\[\begin{aligned} f(x) &= 5-x \quad \color {Red} \text { Original function notation. } \\ f(\;\;) &= 5-(\;\;) \quad \color {Red} \text { Replace each occurrence of } x \text { with open parentheses. } \end{aligned} \nonumber \]

Тепер$−1$ підставляємо$x$ в відкриті дужки, підготовлені на останньому кроці.

\[\begin{aligned} f(-1) &= 5-(-1) \quad \color {Red} \text { Substitute }-1 \text { for } x \text { in the open } \\ &= 5+1 \quad \color {Red}\text { Add the opposite. } \\ &= 6 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]

Таким чином,$f(−1) = 6$. Далі нас просять знайти$g(−2)$. Це означає, що ми повинні замінити кожне входження$x$ з$−2$ у функції$g(x)=x^2 −9$.

\[\begin{aligned} g(x) &= x^{2}-9 \quad \color {Red} \text { Original function notation. } \\ g(\;\;) &= (\;\;)^{2}-9 \quad \color {Red} \text { Replace each occurrence of } x \text { with open parentheses. } \end{aligned} \nonumber \]

Тепер$−2$ підставляємо$x$ в відкриті дужки, підготовлені на останньому кроці.

\[\begin{aligned} g({\color {Red}-2}) &= ({\color {Red}-2})^{2}-9 \quad \color {Red} \text { Substitute }-2 \text { for } x \text { in the open parentheses position. } \\ &= 4-9 \quad \color {Red} \text { Exponent first: }(-2)^{2}=4 \\ &= -5 \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber \]

Таким чином,$g(−2) =−5$.

Вправа$\PageIndex{10}$

Дано$(x)=3x^2 −20$ and $g(x)=4x +6/x$, знахідку$f(−3)$ and $g(2)$.

Відповідь: $f(−3) = 7$і$g(2) = 10$

Взаємозамінні$y$ та$f(x)$

У більшості випадків$y$ і$f(x)$ є повністю взаємозамінними. Наприклад, порівняйте та порівняйте наступні два приклади.

Питання: Задано$y =3 x + 7$, знайдіть,$y$ коли$x$ дорівнює$5$.

Рішення:$x$ Замініть на$5$.

\[\begin{array}{l}{y=3 x+7} \\ {y=3(5)+7} \\ {y=15+7} \\ {y=22}\end{array} \nonumber \]

Питання: Враховуючи$f(x)=3 x + 7$, оцінюйте$f(5)$

Рішення:$x$ Замініть на$5$.

\[\begin{array}{l}{f(x)=3 x+7} \\ {f(5)=3(5)+7} \\ {f(5)=15+7} \\ {f(5)=22}\end{array} \nonumber \]

У кожному конкретному випадку відповідь є$22$. Однак у першому випадку відповідь$y = 22$ маскує той факт, що для отримання результату$5$ було використано$x$ значення -value of. З іншого боку, коли ми використовуємо позначення функції, кінцева відповідь$f(5) = 22$ вказує на те, що ми використовували$x$ -значення,$5$ щоб визначити, що$y$ -value є$22$. Це ще одна перевага позначення функцій.

Давайте розглянемо одну остаточну програму, яка демонструє, що$y$ і$f(x)$ є взаємозамінними.

Приклад$\PageIndex{11}$

Намалюйте графік$f(x)=2x−3$.

Рішення

Оскільки$y$ і$f(x)$ є взаємозамінними, інструкція ідентична «ескізу графіка»$y =2 x−3$. Графік являє собою пряму, з нахилом$2$ і$y$ -перехопленням на$(0,−3)$. Побудуйте$y$ -перехоплення на$(0,−3)$, потім рухайтеся вгору$2$ і вправо,$1$ щоб створити лінію з нахилом$2$ (див. Малюнок$\PageIndex{10}$). Зверніть увагу, як ми позначили графік з його рівнянням за допомогою позначення функції.

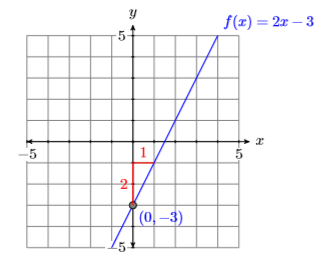
рис. 5.1.10.png — Малюнок$\PageIndex{10}$: Графік$f(x)=2x−3$ є лінією.

Вправа$\PageIndex{11}$

Намалюйте графік$f(x)=-\dfrac{2}{3} x-2$

Відповідь: $Ех 5.1.11.png$

Картографічні діаграми

Визначення функції

Позначення діаграми відображення

Функція позначення

Взаємозамінні\(y\) та\(f(x)\)