5.5: Закони експонентів

У розділі 1 глави 1 ми вперше ввели визначення показника. Для зручності повторюємо це визначення.

У$a^n$ експоненціальному$a$ виразі число називається базовим, тоді як число$n$ називається показником.

Показники

$a$Дозволяти бути будь-яке дійсне число і нехай$n$ бути будь-яке ціле число. Якщо$n \neq 0$, то:

$$a^{n}=\underbrace{a \cdot a \cdot a \cdots \cdot a}_{n \text { times }} \nonumber$$

Тобто обчислити$a^n$, записувати$a$ як множник$n$ раз. У разі де$a \neq 0$, але$n = 0$, то визначаємо:

$$a^0 =1 \nonumber$$

Наприклад, підняття числа до п'ятої потужності вимагає повторення числа як множника п'ять разів (див. Рис.$\PageIndex{1}$).

$$\begin{aligned}(-2)^{5} &=(-2)(-2)(-2)(-2)(-2) \\ &=-32 \end{aligned} \nonumber$$

Малюнок$\PageIndex{1}$: Оцінка$(−2)^5$ і$(−1/2)^4$. Нагадаємо: Використовуйте клавішу MATH, щоб знайти команду ► Frac.

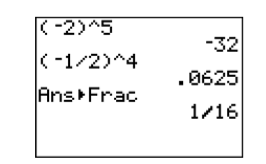
Підвищення числа до четвертої потужності вимагає повторення цього числа як множника чотири рази (див. Рис.$\PageIndex{1}$).

$$\begin{aligned}\left(-\dfrac{1}{2}\right)^{4} &=\left(-\dfrac{1}{2}\right)\left(-\dfrac{1}{2}\right)\left(-\dfrac{1}{2}\right)\left(-\dfrac{1}{2}\right) \\ &=\dfrac{1}{16} \end{aligned} \nonumber$$

В якості заключного прикладу зверніть увагу на те$10^0 = 1$, що, але$0^0$ не визначено (див. Рис.$\PageIndex{2}$).

Малюнок$\PageIndex{2}$: Оцінка$10^0$ і$0^0$ на графічному калькуляторі.

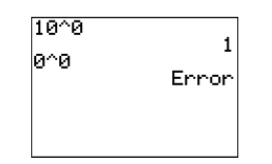
Примітка

Для тих, хто може бути цікаво чому$a^0 = 1$, provided $a \neq 0$, ось хороший аргумент. По-перше, зверніть увагу, що$a^1 = a$, so:

$$a \cdot a^{0}=a^{1} \cdot a^{0} \nonumber$$

Праворуч повторіть базу і додайте експоненти.

$$a \cdot a^{0}=a^{1} \nonumber$$

Або еквівалентно:

$$a \cdot a^{0}=a \nonumber$$

Тепер розділіть обидві сторони$a$, which is допустимими, якщо$a \neq 0$.

$$\dfrac{a \cdot a^{0}}{a}=\dfrac{a}{a} \nonumber$$

Спростити обидві сторони:

$$a^0 =1 \nonumber$$

Множення з подібними основами

У$a^n$ виразі число$a$ називається базовим, а число$n$ називається показником. Часто нам потрібно буде помножити два експоненціальні вирази з подібними основами, наприклад$x^{3} \cdot x^{4}$. Нагадаємо, що показник підказує нам, скільки разів писати кожну базу як фактор, щоб ми могли написати:

$$\begin{aligned} x^{3} \cdot x^{4} &=(x \cdot x \cdot x) \cdot(x \cdot x \cdot x \cdot x) \\ &=x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x \\ &=x^{7} \end{aligned} \nonumber$$

Зверніть увагу, що ми просто підраховуємо кількість разів, що$x$ виникає як фактор. Спочатку у нас є три$x’s$, потім чотири$x’s$, загалом сім$x’s$. Однак невелика думка говорить нам, що набагато швидше просто додати експоненти, щоб виявити загальну кількість разів$x$ відбувається як фактор.

$$\begin{aligned} x^{3} \cdot x^{4} &=x^{3+4} \\ &=x^{7} \end{aligned} \nonumber$$

Попереднє обговорення є прикладом наступного загального закону експонентів.

Множення з подібними основами

Щоб помножити два експоненціальні вирази з подібними основами, повторіть базу і додайте показники.

$$a^{m} \cdot a^{n}=a^{m+n} \nonumber$$

Приклад$\PageIndex{1}$

Спростіть кожне з наведених нижче виразів:

1. $y^{4} \cdot y^{8}$
2. $2^{3} \cdot 2^{5}$
3. $(x+y)^{2}(x+y)^{7}$

Рішення

У кожному прикладі ми маємо подібні основи. Таким чином, підхід буде однаковим для кожного прикладу: повторіть базу і додайте показники.

1. $\begin{aligned} y^{4} \cdot y^{8} &=y^{4+8} \\ &=y^{12} \end{aligned}$
2. $\begin{aligned} 2^{3} \cdot 2^{5} &=2^{3+5} \\ &=2^{8} \end{aligned}$
3. $\begin{aligned}(x+y)^{2}(x+y)^{7} &=(x+y)^{2+7} \\ &=(x+y)^{9} \end{aligned}$

Трохи потренувавшись, кожен з прикладів можна спростити подумки. Повторіть базу і додайте експоненти в голові:$y^{4} \cdot y^{8}=y^{12}, 2^{3} \cdot 2^{5}=2^{8}$ і$(x+y)^{2}(x+y)^{7}=(x+y)^{9}$.

Вправа$\PageIndex{1}$

$3^{4} \cdot 3^{2}$

Відповідь

$3^6$

Приклад$\PageIndex{2}$

Спростити:$\left(a^{6} b^{4}\right)\left(a^{3} b^{2}\right)$

Рішення

Ми будемо використовувати комутативні та асоціативні властивості, щоб змінити порядок роботи, а потім повторити загальні основи та додати показники.

$$\begin{aligned} \left(a^{6} b^{4}\right)\left(a^{3} b^{2}\right) &= a^{6} b^{4} a^{3} b^{2} \quad \color {Red} \text { The associative property allows us to regroup in the order we prefer. } \\ &= a^{6} a^{3} b^{4} b^{2} \quad \color {Red} \text { The commutative property allows us to change the order of multiplication. } \\ &= a^{9} b^{6} \quad \color {Red} \text { Repeat the common bases and add the exponents. } \end{aligned} \nonumber$$

З практикою ми розуміємо, що якщо всі оператори множення, то ми можемо множити в тому порядку, який ми віддаємо перевагу, повторюючи загальні основи та додаючи показники подумки:$\left(a^{6} b^{4}\right)\left(a^{3} b^{2}\right)=a^{9} b^{6}$.

Вправа$\PageIndex{2}$

$\left(x^{2} y^{6}\right)\left(x^{4} y^{3}\right)$

Відповідь

$x^{6} y^{9}$

Приклад$\PageIndex{3}$

Спростити:$x^{n+3} \cdot x^{3-2 n}$

Рішення

Знову повторюємо базу і додаємо експоненти.

$$\begin{aligned} x^{n+3} \cdot x^{3-2 n} &= x^{(n+3)+(3-2 n)} \quad \color {Red}\text { Repeat the base, add the exponents. } \\ &= x^{6-n} \quad \color {Red} \text { Simplify. Combine like terms. } \end{aligned} \nonumber$$

Вправа$\PageIndex{3}$

$x^{5-n} \cdot x^{4 n+2}$

Відповідь

$x^{3 n+7}$

Поділ подібними основами

Як і множення, нас також часто просять розділити експоненціальні вирази подібними основами, такими як$x^7/x^4$. Знову ж таки, ключ полягає в тому, щоб пам'ятати, що показник говорить нам, скільки разів писати базу як фактор, щоб ми могли написати:

$$\begin{aligned} \dfrac{x^{7}}{x^{4}} &= \dfrac{x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x}{x \cdot x \cdot x \cdot x} \\ &= \dfrac{\not {x} \cdot \not {x} \cdot \not{x} \cdot \not {x} \cdot x \cdot x \cdot x}{\not {x} \cdot \not {x} \cdot \not {x} \cdot \not {x}} \\ &= x^3 \end{aligned} \nonumber$$

Зверніть увагу, як ми скасуємо чотири$x’s$ в чисельнику для чотирьох$x’s$ в знаменнику. Однак у певному сенсі ми «віднімаємо чотири$x’s$» з чисельника, тому швидший спосіб продовжити - повторити базу та відняти показники наступним чином:

$$\begin{aligned} \dfrac{x^{7}}{x^{4}} &=x^{7-4} \\ &=x^{3} \end{aligned} \nonumber$$

Попереднє обговорення є прикладом другого загального закону експонентів.

Як розділити за допомогою подібних основ

Щоб розділити два експоненціальні вирази подібними основами, повторіть базу і відніміть показники. Враховуючи$a \neq 0$,

$$\dfrac{a^{m}}{a^{n}}=a^{m-n} \nonumber$$

Зверніть увагу, що віднімання показників слід правилу «верх мінус низ».

Примітка

Ось ще один приємний аргумент чому$a^0 = 1$, за умови$a \neq 0$. Почніть з:

$$\dfrac{a^{1}}{a^{1}}=1 \nonumber$$

Повторіть базу і відніміть показники.

$$a^{1-1}=1 \nonumber$$

Спростити.

$$a^0 = 1 \nonumber$$

Приклад$\PageIndex{4}$

Спростіть кожне з наведених нижче виразів:

1. $\dfrac{x^{12}}{x^{3}}$
2. $\dfrac{5^{7}}{5^{7}}$
3. $\dfrac{(2 x+1)^{8}}{(2 x+1)^{3}}$

Рішення

У кожному прикладі ми маємо подібні основи. Таким чином, підхід буде однаковим для кожного прикладу: повторіть базу і відніміть показники.

1. $\begin{aligned} \dfrac{x^{12}}{x^{3}} &=x^{12-3} \\ &=x^{9} \end{aligned}$
2. $\begin{aligned} \dfrac{5^{7}}{5^{7}} &=5^{7-7} \\ &=5^{0} \\ &=1 \end{aligned}$
3. $\begin{aligned} \dfrac{(2 x+1)^{8}}{(2 x+1)^{3}} &=(2 x+1)^{8-3} \\ &=(2 x+1)^{5} \end{aligned}$

Трохи потренувавшись, кожен з прикладів можна спростити подумки. Повторіть базу і відніміть показники в голові:$x^{12} / x^{3}=x^{9}, 5^{7} / 5^{4}=5^{3}$ і$(2 x+1)^{8} /(2 x+1)^{3}=(2 x+1)^{5}$.

Вправа$\PageIndex{4}$

$\dfrac{4^{5}}{4^{3}}$

Відповідь

$4^2$

Приклад$\PageIndex{5}$

Спростити:$\dfrac{12 x^{5} y^{7}}{4 x^{3} y^{2}}$

Рішення

Ми спочатку виражаємо дріб як добуток трьох дробів, останні дві із загальною основою. У першому рядку наступного рішення зверніть увагу, що якщо помножити чисельники та знаменники трьох окремих дробів, добуток дорівнює вихідному дробу зліва.

$$\begin{aligned} \dfrac{12 x^{5} y^{7}}{4 x^{3} y^{2}} &= \dfrac{12}{4} \cdot \dfrac{x^{5}}{x^{3}} \cdot \dfrac{y^{7}}{y^{2}} \quad \color {Red} \text { Break into a product of three fractions. } \\ &= 3 x^{5-3} y^{7-2} \quad \color {Red} \text { Simplify: } 12 / 4=3 . \text { Then repeat the common } \\ &= 3 x^{2} y^{5} \quad \color {Red} \text { Simplify. } \end{aligned} \nonumber$$

Вправа$\PageIndex{5}$

Спростити:$\dfrac{15 a^{6} b^{9}}{3 a b^{5}}$

Відповідь

$5 a^{5} b^{4}$

Приклад$\PageIndex{6}$

Спростити:$\dfrac{x^{5 n-4}}{x^{3-2 n}}$

Рішення

Знову повторюємо базу і віднімаємо показники.

$$\begin{aligned} \dfrac{x^{5 n-4}}{x^{3-2 n}} &= x^{(5 n-4)-(3-2 n)} \quad \color {Red} \text { Repeat the base, subtract exponents. } \\ &= x^{5 n-4-3+2 n} \quad \color {Red} \text { Distribute the minus sign. } \\ &= x^{7 n-7} \quad \color {Red} \text { Simplify. Combine like terms. } \end{aligned} \nonumber$$

Вправа$\PageIndex{6}$

Спростити:$\dfrac{x^{3 n-6}}{x^{n+2}}$

Відповідь

$x^{2 n-8}$

Підняття влади до влади

Припустимо, у нас є експоненціальний вираз, піднятий до другої сили, наприклад$(x^2)3$. Другий показник говорить нам писати$x^2$ як фактор три рази:

$$\begin{aligned} \left(x^{2}\right)^{3} &= x^{2} \cdot x^{2} \cdot x^{2} \quad \color {Red} \text { Write } x^{2} \text { as a factor three times. } \\ &= x^{6} \quad \color {Red} \text { Repeat the base, add the exponents. } \end{aligned} \nonumber$$

Зверніть увагу, як ми додали$2 + 2 + 2$, щоб отримати$6$. Однак набагато швидший спосіб додати «три двійки» - множити:$3 \cdot 2=6$. Таким чином, піднімаючи «силу до другої потужності», повторіть базу і помножте показники наступним чином:

$$\begin{aligned}\left(x^{2}\right)^{3} &=x^{2 \cdot 3} \\ &=x^{6} \end{aligned} \nonumber$$

Попереднє обговорення породжує наступний третій закон експонентів.

Підняття влади до влади

Піднімаючи силу до степені, повторіть базу і помножте показники. У символах:
$$(a^m)^n = a^{mn} \nonumber$$
Зверніть увагу, що зіставлення двох змінних, як у$mn$, означає «$m$раз»$n$.

Приклад$\PageIndex{7}$

Спростіть кожне з наведених нижче виразів:

1. $\left(z^{3}\right)^{5}$
2. $\left(7^{3}\right)^{0}$
3. $\left[(x-y)^{3}\right]^{6}$

Рішення

У кожному прикладі ми піднімаємо владу до влади. Отже, в кожному випадку повторюємо базу і множимо показники.

1. $\begin{aligned}\left(z^{3}\right)^{5} &=z^{3.5} \\ &=z^{15} \end{aligned}$
2. $\begin{aligned}\left(7^{3}\right)^{0} &=7^{3.0} \\ &=7^{0} \\ &=1 \end{aligned}$
3. $\begin{aligned}\left[(x-y)^{3}\right]^{6} &=(x-y)^{3 \cdot 6} \\ &=(x-y)^{18} \end{aligned}$

Трохи потренувавшись, кожен з прикладів можна спростити подумки. Повторіть базу і помножте показники в голові:$\left(z^{3}\right)^{5}=z^{15},\left(7^{3}\right)^{4}=7^{12}$ і$\left[(x-y)^{3}\right]^{6}=(x-y)^{18}$.

Вправа$\PageIndex{7}$

Спростити:$\left(2^{3}\right)^{4}$

Відповідь

$2^{12}$

Приклад$\PageIndex{8}$

Спростити:$\left(x^{2 n-3}\right)^{4}$

Рішення

Знову повторюємо базу і множимо показники.

$$\begin{aligned} \left(x^{2 n-3}\right)^{4} &= x^{4(2 n-3)} \quad \color {Red} \text { Repeat the base, multiply exponents. } \\ &= x^{8 n-12} \quad \color {Red} \text { Distribute the } 4 . \end{aligned} \nonumber$$

Вправа$\PageIndex{8}$

Спростити:$\left(a^{2-n}\right)^{3}$

Відповідь

$a^{6-3 n}$

Підняття продукту до влади

Нам часто доводиться піднімати продукт до влади, наприклад$(xy)^3$. Знову ж таки, пам'ятайте, що показник говорить нам писати$xy$ як фактор три рази, так:

$$\begin{aligned} (x y)^{3} &=(x y)(x y)(x y) \quad \color {Red} \text {Write } xy \text { as a factor three times.}\\ &=x y x y x y \quad \color {Red} \text {The associative property allows us to group as we please.}\\ &=x x x y y y \quad \color {Red} \text {The commutative property allows us to change the order as we please.}\\ &=x^{3} y^{3} \quad \color {Red} \text {Invoke the exponent definition: } x x x=x^{3} \text { and } y y y=y^{3} \end{aligned} \nonumber$$

Однак набагато простіше зазначити, що коли ви піднімаєте продукт до влади, ви піднімаєте кожен фактор до цієї сили. У символах: $$(xy)^3 = x^3y^3 \nonumber$$
Попереднє обговорення призводить нас до четвертого закону експонентів.

Підняття продукту до влади

Щоб підняти продукт до влади, підніміть кожен фактор до цієї сили. В символах:

$$(ab)^n = a^nb^n \nonumber$$

Приклад$\PageIndex{9}$

Спростіть кожне з наведених нижче виразів:

1. $(y z)^{5}$
2. $(-2 x)^{3}$
3. $(-3 y)^{2}$

Рішення

У кожному прикладі ми піднімаємо продукт до влади. Отже, у кожному конкретному випадку ми піднімаємо кожен фактор до цієї сили.

1. $(y z)^{5}=y^{5} z^{5}$
2. $\begin{aligned}(-2 x)^{3} &=(-2)^{3} x^{3} \\ &=-8 x^{3} \end{aligned}$
3. $\begin{aligned}(-3 y)^{2} &=(-3)^{2} y^{2} \\ &=9 y^{2} \end{aligned}$

Трохи потренувавшись, кожен з прикладів можна спростити подумки. Підніміть кожен фактор до зазначеної потужності в голові:$(y z)^{5}=y^{5} z^{5},(-2 x)^{3}=-8 x^{3}$ і$(-3 y)^{2}=9 y^{2}$

Вправа$\PageIndex{9}$

Спростити:$(-2 b)^{4}$

Відповідь

$16 b^{4}$

Піднімаючи добуток трьох факторів до влади, легко показати, що ми повинні підняти кожен фактор до зазначеної потужності. Наприклад,$(a b c)^{3}=a^{3} b^{3} c^{3}$. Взагалі, це справедливо незалежно від кількості факторів. Піднімаючи продукт до потужності, підніміть кожен з факторів до зазначеної потужності.

Приклад$\PageIndex{10}$

Спростити:$\left(-2 a^{3} b^{2}\right)^{3}$

Рішення

Підніміть кожен фактор до третьої потужності, потім спрощуйте.

$$\begin{aligned} \left(-2 a^{3} b^{2}\right)^{3} &= (-2)^{3}\left(a^{3}\right)^{3}\left(b^{2}\right)^{3} \quad \color {Red} \text { Raise each factor to the third power. } \\ &= -8 a^{9} b^{6} \quad \color {Red} \text {Simplify: } (-2)^{3}=8 \text {. In the remaining factors, raising a power to a power requires that we multiply the exponents. } \end{aligned} \nonumber$$

Вправа$\PageIndex{10}$

Спростити:$\left(-3 x y^{4}\right)^{5}$

Відповідь

$-243 x^{5} y^{20}$

Приклад$\PageIndex{11}$

Спростити:$\left(-2 x^{2} y\right)^{2}\left(-3 x^{3} y\right)$

Рішення

У першому згрупованому продукті підніміть кожен фактор до другої потужності.

$$\begin{aligned} \left(-2 x^{2} y\right)^{2}\left(-3 x^{3} y\right) &=\left((-2)^{2}\left(x^{2}\right)^{2} y^{2}\right)\left(-3 x^{3} y\right) \quad \color {Red} \text { Raise each factor in the first grouped product to the second power.} \\ &=\left(4 x^{4} y^{2}\right)\left(-3 x^{3} y\right) \quad \color {Red} \text { Simplify: } (-2)^{2}=4 \text { and } \left(x^{2}\right)^{2}=x^{4} \end{aligned} \nonumber$$

Асоціативне і комутативне властивість дозволяє множити всі шість факторів в тому порядку, який нам подобається. Отже, ми будемо множити$4$ і$−3$, потім$x^4$ і$x^3$, і\ (y^2 і y, в такому порядку. В цьому випадку повторюємо базу і додаємо експоненти.

$$\begin{aligned} &=-12x^7y^3 \quad \color {Red} \text { Simplify: } (4)(-3)=-12. \text { Also, } x^{4}x^3=x^{7} \text { and } y^2y = y^3\end{aligned} \nonumber$$

Вправа$\PageIndex{11}$

Спростити:$\left(-a^{3} b^{2}\right)^{3}\left(-2 a^{2} b^{4}\right)^{2}$

Відповідь

$-4 a^{13} b^{14}$

Підвищення частки до влади

Підвищення частки до влади схоже на підвищення продукту до влади. Наприклад, підвищення$(x/y)^3$ вимагає, щоб ми писали$x/y$ як фактор тричі.

$$\begin{aligned}\left(\frac{x}{y}\right)^{3} &=\frac{x}{y} \cdot \frac{x}{y} \cdot \frac{x}{y} \\ &=\frac{x \cdot x \cdot x}{y \cdot y \cdot y} \\ &=\frac{x^{3}}{y^{3}} \end{aligned} \nonumber$$

Однак набагато простіше усвідомити, що коли ви піднімаєте частку до степеня, ви піднімаєте і чисельник, і знаменник до цієї влади. В символах:

$$\left(\dfrac{x}{y}\right)^{3}=\frac{x^{3}}{y^{3}} \nonumber$$

Це призводить до п'ятого і останнього закону експонентів.

Підвищення частки до влади

Щоб підняти частку до степеня, підніміть і чисельник, і знаменник до цієї влади. Враховуючи$b \neq 0$,

$$\left(\dfrac{a}{b}\right)^{n}=\dfrac{a^{n}}{b^{n}} \nonumber$$

Приклад$\PageIndex{12}$

Спростіть кожне з наведених нижче виразів:

1. $\left(\dfrac{2}{3}\right)^{2}$
2. $\left(\dfrac{x}{3}\right)^{3}$
3. $\left(-\dfrac{2}{y}\right)^{4}$

Рішення

У кожному прикладі ми піднімаємо частку до влади. Отже, в кожному випадку ми піднімаємо і чисельник, і знаменник до цієї міри.

1. $\begin{aligned}\left(\dfrac{2}{3}\right)^{2} &=\dfrac{2^{2}}{3^{2}} \\ &=\dfrac{4}{9} \end{aligned}$
2. $\begin{aligned}\left(\dfrac{x}{3}\right)^{3} &=\dfrac{x^{3}}{3^{3}} \\ &=\dfrac{x^{3}}{27} \end{aligned}$
3. $\begin{aligned}\left(-\dfrac{2}{y}\right)^{4} &=\dfrac{2^{4}}{y^{4}} \\ &=\dfrac{16}{y^{4}} \end{aligned}$

Зверніть увагу, що в прикладі (c) підвищення негативної бази до рівної потужності дає позитивний результат. Трохи потренувавшись, кожен з прикладів можна спростити подумки. Підніміть чисельник і знаменник до зазначеної потужності в голові:$(2 / 3)^{2}=4 / 9,(x / 3)^{3}=x^{3} / 27,$ і$(-2 / y)^{4}=16 / y^{4}$

Вправа$\PageIndex{12}$

Спростити:$\left(\dfrac{5}{4}\right)^{3}$

Відповідь

$\dfrac{125}{64}$

Приклад$\PageIndex{13}$

Спростити:$\left(\dfrac{2 x^{5}}{y^{3}}\right)^{2}$

Рішення

Підніміть і чисельник, і знаменник до другого ступеня, потім спростіть:

$$\begin{aligned} \left(\dfrac{2 x^{5}}{y^{3}}\right)^{2}=\dfrac{\left(2 x^{5}\right)^{2}}{\left(y^{3}\right)^{2}} \quad \color {Red} \text {Raise numerator and denominator to the second power.} \end{aligned} \nonumber$$

У чисельнику нам потрібно підняти кожен множник добутку до другого ступеня. Тоді нам потрібно нагадати собі, що коли ми піднімаємо силу до сили, ми множимо показники.

$$\begin{aligned} &= \dfrac{2^{2}\left(x^{5}\right)^{2}}{\left(y^{3}\right)^{2}} \quad \color {Red} \text {Raise each factor in the numerator and denominator to the second power.} \\ &= \dfrac{4 x^{10}}{y^{6}} \quad \color {Red} \text { Simplify: } 2^{2}=4,\left(x^{5}\right)^{2}=x^{10} \text {, and } (y^3)^2=y^6 \end{aligned} \nonumber$$

Вправа$\PageIndex{13}$

Спростити:$\left(\dfrac{a^{4}}{3 b^{2}}\right)^{3}$

Відповідь

$\dfrac{a^{12}}{27 b^{6}}$