5.4: Додавання та віднімання многочленів

Last updated
Save as PDF

Page ID: 58280

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У цьому розділі ми зосереджуємося на додаванні та відніманні поліноміальних виразів, заснованих на попередніх роботах, що поєднують подібні терміни у висхідній та спадній силах. Почнемо з прикладу додавання.

Приклад$\PageIndex{1}$

Спростити:\[\left(a^{2}+3 a b-b^{2}\right)+\left(4 a^{2}+11 a b-9 b^{2}\right) \nonumber \]

Рішення

Використовуйте комутативні та асоціативні властивості, щоб змінити порядок і перегрупувати. Потім комбінуйте подібні терміни.

\[\begin{aligned}\left(a^{2}+3 a b-b^{2}\right) &+\left(4 a^{2}+11 a b-9 b^{2}\right) \\ &=\left(a^{2}+4 a^{2}\right)+(3 a b+11 a b)+\left(-b^{2}-9 b^{2}\right) \\ &=5 a^{2}+14 a b-10 b^{2} \end{aligned} \nonumber \]

Вправа$\PageIndex{1}$

Спростити:$\left(3 s^{2}-2 s t+4 t^{2}\right)+\left(s^{2}+7 s t-5 t^{2}\right)$

Відповідь: $4 s^{2}+5 s t-t^{2}$

Давайте об'єднаємо деякі поліноміальні функції.

Приклад$\PageIndex{2}$

Дано$f(x)=3x^2−4x−8$ і$g(x)=x^2−11x+15$, спростити$f(x)+g(x)$.

Рішення

По-перше, замінити$f(x)$ і$g(x)$ з їх визначеннями. Обов'язково оточуйте кожен многочлен дужками, тому що нас просять додати все$f(x)$ до всіх$g(x)$.

\[f(x)+g(x) = (3x^2 −4x−8) + (x^2 −11x + 15) \nonumber \]Тепер використовуйте комутативні та асоціативні властивості, щоб змінити порядок і перегрупувати. Поєднуйте подібні терміни.

\[\begin{array}{l}{=\left(3 x^{2}+x^{2}\right)+(-4 x-11 x)+(-8+15)} \\ {=4 x^{2}-15 x+7}\end{array} \nonumber \]

Отже,$f(x)+g(x)=4x^2 −15x + 7$.

Вправа$\PageIndex{2}$

Дайте en$f(x)=2x^2 +9x−5$ і$g(x)=−x^2 −4x + 3$, simplify $f(x)+g(x)$.

Відповідь: $x^{2}+5 x-2$

Якщо вам зручно пропустити крок або два, не обов'язково записувати всі кроки, показані в Прикладах$\PageIndex{1}$ і$\PageIndex{2}$. Спробуємо поєднати подібні терміни подумки в наступному прикладі.

Приклад$\PageIndex{3}$

Спростити:\[\left(x^{3}-2 x^{2} y+3 x y^{2}+y^{3}\right)+\left(2 x^{3}-4 x^{2} y-8 x y^{2}+5 y^{3}\right) \nonumber \]

Рішення

Якщо ми використовуємо асоціативну та комутативну властивість для переупорядкування та перегрупування, то об'єднаємо подібні терміни, отримаємо наступний результат.

\[\begin{aligned}\left(x^{3}-2 x^{2} y\right.&+3 x y^{2}+y^{3} )+\left(2 x^{3}-4 x^{2} y-8 x y^{2}+5 y^{3}\right) \\ &=\left(x^{3}+2 x^{3}\right)+\left(-2 x^{2} y-4 x^{2} y\right)+\left(3 x y^{2}-8 x y^{2}\right)+\left(y^{3}+5 y^{3}\right) \\ &=3 x^{3}-6 x^{2} y-5 x y^{2}+6 y^{3} \end{aligned} \nonumber \]

Однак якщо ми можемо поєднувати подібні терміни подумки, усуваючи середню сходинку, набагато ефективніше написати:

\[\begin{array}{l}{\left(x^{3}-2 x^{2} y+3 x y^{2}+y^{3}\right)+\left(2 x^{3}-4 x^{2} y-8 x y^{2}+5 y^{3}\right)} \\ {\quad \quad=3 x^{3}-6 x^{2} y-5 x y^{2}+6 y^{3}}\end{array} \nonumber \]

Вправа$\PageIndex{3}$

Спростити:$\left(-5 a^{2} b+4 a b-3 a b^{2}\right)+\left(2 a^{2} b+7 a b-a b^{2}\right)$

Відповідь: $-3 a^{2} b+11 a b-4 a b^{2} d$

Заперечуючи многочлен

Перш ніж спробувати віднімання многочленів, давайте спочатку розглянемо, як заперечувати або «прийняти протилежне» многочлена. Спочатку нагадаємо, що заперечення еквівалентно множенню на$−1$.

заперечуючи

Якщо$a$ будь-яке число, то

\[−a =(−1)a. \nonumber \]

Тобто заперечення еквівалентно множенню на$−1$.

Ми можемо використовувати цю властивість для спрощення$−(a + b)$. По-перше, заперечення ідентично множенню на$−1$. Тоді ми можемо розподілити$−1$.

\[\begin{aligned} -(a+b) &= (-1)(a+b) \quad \color {Red} \text { Negating is equivalent to multiplying by } -1 \\ &= (-1) a+(-1) b \quad \color {Red} \text { Distribute the }-1 . \\ &= -a+(-b) \quad \color {Red} \text { Simplify: }(-1) a=-a \text { and }(-1) b=-b \\ &= -a-b \quad \color {Red} \text { Subtraction means add the opposite. } \end{aligned} \nonumber \]

Таким чином,$−(a + b)=−a −b$. Однак, ймовірно, простіше відзначити, що знак мінус перед дужками просто змінював знак кожного члена всередині дужок.

заперечення суми

При запереченні суми термінів дія знака мінус полягає в зміні кожного члена в дужках на протилежний знак. \[−(a + b)=−a−b \nonumber \]

Давайте розглянемо цей принцип в наступному прикладі.

Приклад$\PageIndex{4}$

Спростити:$-\left(-3 x^{2}+4 x-8\right)$

Рішення

По-перше, заперечення еквівалентно множенню на$−1$. Потім розподіліть$−1$.

\[\begin{aligned} -&\left(-3 x^{2}+4 x-8\right) \\ &=(-1)\left(-3 x^{2}+4 x-8\right) \quad \color {Red} \text{Negating is equivalent to multiplying by } -1\\ &=(-1)\left(-3 x^{2}\right)+(-1)(4 x)-(-1)(8) \quad \color {Red} \text {Distribute the } -1 \\ &=3 x^{2}+(-4 x)-(-8) \quad \color {Red} \text {Simplify: } (-1)(-3 x^{2})=3 x^{2}, (-1)(4 x)=-4 x, \text {and} (-1)(8)=-8\\ &=3 x^{2}-4 x+8 \quad \color {Red} \text {Subtraction means add the opposite.} \end{aligned} \nonumber \]

Альтернативне рішення:

Як ми бачили вище, негативний знак перед дужками просто змінює знак кожного члена всередині дужок. Так що набагато ефективніше писати\[−(−3x^2 +4x−8) = 3x^2 −4x +8 \nonumber \] просто змінюючи знак кожного члена всередині дужок.

Вправа$\PageIndex{4}$

Спростити:$-\left(2 x^{2}-3 x+9\right)$

Відповідь: $-2 x^{2}+3 x-9$

Віднімання многочленів

Тепер, коли ми знаємо, як звести нанівець многочлен (змінити знак кожного члена многочлена), ми готові відняти многочлени.

Приклад$\PageIndex{5}$

Спростити:$\left(y^{3}-3 y^{2} z+4 y z^{2}+z^{3}\right)-\left(2 y^{3}-8 y^{2} z+2 y z^{2}-8 z^{3}\right)$

Рішення

Спочатку розподіліть знак мінус, змінюючи знак кожного члена другого многочлена.

\[\left(y^{3}-3 y^{2} z+4 y z^{2}+z^{3}\right)-\left(2 y^{3}-8 y^{2} z+2 y z^{2}-8 z^{3}\right)=y^{3}-3 y^{2} z+4 y z^{2}+z^{3}-2 y^{3}+8 y^{2} z-2 y z^{2}+8 z^{3} \nonumber \]

Перегрупувати, комбінуючи подібні терміни. Ви можете виконати цей наступний крок подумки, якщо хочете.

\[\begin{array}{l}{=\left(y^{3}-2 y^{3}\right)+\left(-3 y^{2} z+8 y^{2} z\right)+\left(4 y z^{2}-2 y z^{2}\right)+\left(z^{3}+8 z^{3}\right)} \\ {=-y^{3}+5 y^{2} z+2 y z^{2}+9 z^{3}}\end{array} \nonumber \]

Вправа$\PageIndex{5}$

Спростити:$\left(4 a^{2} b+2 a b-7 a b^{2}\right)-\left(2 a^{2} b-a b-5 a b^{2}\right)$

Відповідь: $2 a^{2} b+3 a b-2 a b^{2}$

Віднімемо дві поліноміальні функції.

Приклад$\PageIndex{6}$

Дано$p(x)=−5x^3 +6 x − 9$ і$q(x)=6 x^2 − 7x − 11$, спростити$p(x)−q(x)$.

Рішення

По-перше, замінити$p(x)$ і$q(x)$ з їх визначеннями. Тому що нас просять відняти все$q(x)$ з усіх$p(x)$, дуже важливо оточити кожен многочлен дужками.

\[p(x)-q(x)=\left(-5 x^{3}+6 x-9\right)-\left(6 x^{2}-7 x-11\right) \nonumber \]

Розподіліть знак мінус, змінюючи знак кожного члена в другому многочлені, потім перегрупуйте і об'єднайте подібні терміни.

\[\begin{array}{l}{=-5 x^{3}+6 x-9-6 x^{2}+7 x+11} \\ {\color {Red} =-5 x^{3}-6 x^{2}+(6 x+7 x)+(-9+11)} \\ {=-5 x^{3}-6 x^{2}+13 x+2}\end{array} \nonumber \]

Однак після розподілу знака мінус, якщо ми можемо поєднувати подібні терміни подумки, усунувши середню сходинку, набагато ефективніше написати:

\[\begin{aligned} p(x)-q(x) &=\left(-5 x^{3}+6 x-9\right)-\left(6 x^{2}-7 x-11\right) \\ &=-5 x^{3}+6 x-9-6 x^{2}+7 x+11 \\ &=-5 x^{3}-6 x^{2}+13 x+2 \end{aligned} \nonumber \]

Вправа$\PageIndex{6}$

Дано$f(x)=3x^2 +9x−4$ і$g(x)=−5x2 +4x−6$, спростити$f(x)−g(x)$.

Відповідь: $8 x^{2}+5 x+2$

Деякі програми

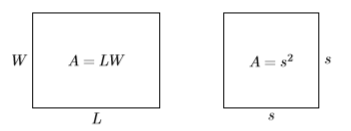
Нагадаємо, що площа прямокутника, що має довжину$L$ і ширину$W$, знаходять за формулою$A = LW$. Площа квадрата, що має сторону s, знаходимо за формулою$A = s^2$ (див. Рис.$\PageIndex{1}$).

рис 5.4.1.png — Малюнок$\PageIndex{1}$: Формули площі для прямокутника та квадрата.

Приклад$\PageIndex{7}$

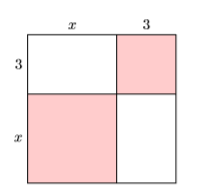
Знайдіть площу квадрата$\PageIndex{2}$ на малюнку, підсумовуючи площу його частин.

рис. 5.4.2.png — Малюнок$\PageIndex{2}$: Знайти суму частин.

Рішення

Давайте відокремлюємо кожну з чотирьох частин і позначимо кожну своєю площею (див. Рис.$\PageIndex{3}$).

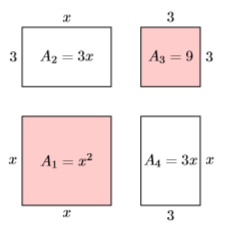
рис. 5.4.3.png — Малюнок$\PageIndex{3}$: Знаходження площі кожної з чотирьох частин.

Два затінених квадрата на малюнку$\PageIndex{3}$ мають області$A_1 = x^2$ та$A_3 = 9$ відповідно. Два незаштрихованих прямокутника на малюнку$\PageIndex{3}$ мають області$A_2 =3 x$ і$A_4 =3x$. Підсумовування цих чотирьох областей дає нам площу всієї фігури.

\[\begin{aligned} A &=A_{1}+A_{2}+A_{3}+A_{4} \\ &=x^{2}+3 x+9+3 x \\ &=x^{2}+6 x+9 \end{aligned} \nonumber \]

Вправа$\PageIndex{7}$

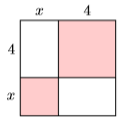
Знайдіть площу квадрата, показаного нижче, підсумовуючи площу його частин.

Відповідь: $x^{2}+8 x+16$

Приклад$\PageIndex{8}$

Імбир веде бізнес з продажу плетених кошиків. Її ділові витрати на виробництво і продаж$x$ плетених кошиків задаються поліноміальною функцією$C(x)=100+3x−0.02x^2$. Дохід, який вона отримує від продажу$x$ плетених кошиків, дається поліноміальної функцією$R(x)=2.75x$. Знайдіть формулу для того$P(x)$, щоб прибуток отримувався від продажу$x$ плетених кошиків. Використовуйте свою формулу, щоб визначити прибуток Джинджер, якщо вона продає$123$ плетені кошики.

Рішення

Прибуток, отриманий від продажу$x$ плетених кошиків, знаходить шляхом віднімання витрат, понесених з отриманого доходу. У символах:\[P(x)=R(x)−C(x) \nonumber \]
Далі, замінити$R(x)$ і$C(x)$ з їх визначеннями. Оскільки ми повинні відняти всю вартість від виручки, обов'язково оточіть поліном вартості дужками. \[P(x)=2 .75x−(100 + 3x−0.02x^2) \nonumber \]
Розподіліть знак мінус і комбінуйте подібні терміни.

\[\begin{array}{l}{=2.75 x-100-3 x+0.02 x^{2}} \\ {=0.02 x^{2}-0.25 x-100}\end{array} \nonumber \]

Таким чином, функція прибутку є$P(x)=0 .02x^2 −0.25x−100$.

Далі, щоб визначити прибуток, якщо продаються$123$ плетені кошики,$123$$x$ замінюємо в функції profit$P(x)$.

\[\begin{aligned} P(x) &=0.02 x^{2}-0.25 x-100 \\ P(123) &=0.02(123)^{2}-0.25(123)-100 \end{aligned} \nonumber \]

Тепер ви можете використовувати графічний калькулятор для визначення прибутку (див. Рисунок$\PageIndex{5}$). Отже, прибуток, отриманий від продажу$123$ плетених кошиків, є$\$171.83$.

рис 5.4.5.png — Малюнок$\PageIndex{5}$: Визначення прибутку від продажу$123$ плетених кошиків.

Вправа$\PageIndex{8}$

Витрати на отримання та продаж$x$ widgets are given by the polynomial function $C(x) = 50 + 5x−0.5x^2$, and the revenue for selling $x$ widgets is given by the polynomial function $R(x)=3.5x$. Determine the прибутку, якщо$75$ widgets are sold.

Відповідь: $\$ 2,650$