5.2: Поліноми

Last updated
Save as PDF

Page ID: 58289

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Починаємо з визначення терміна.

Визначення: Термін

Термін - це або одне число (зване постійним терміном), або добуток числа і однієї або декількох змінних.

Наприклад, кожне з наступних є терміном.

\[ -5 \quad-3 x^{2} \quad 12 y^{2} z^{3} \quad 13 a^{2} b c^{3} \nonumber \]

Зверніть увагу, що перший термін є єдиним числом, тоді як інші терміни є добутком числа та однієї або декількох змінних. Наприклад,$−3x^2$ це продукт$−3$$x$, і$x$.

Визначення: коефіцієнт

Коли термін є добутком числа і однієї або декількох змінних, число називається коефіцієнтом терміна. У випадку терміна, який є єдиним числом, саме число називається коефіцієнтом.

Так, наприклад, коефіцієнти термінів\[-5 \quad-3 x^{2} \quad 12 y^{2} z^{3} \quad 13 a^{2} b c^{3} \nonumber \] є$−5$,$−3$, і$12$$13$, відповідно.

Визначення: Ступінь

Ступінь члена - це сума показників на кожній змінній терміна. Постійний член (єдине число без змінних) має нульовий ступінь.

Таким чином, наприклад, ступені термінів\[-5 \quad-3 x^{2} \quad 12 y^{2} z^{3} \quad 13 a^{2} b c^{3} \nonumber \] є$0$,$2$$5$, і$6$, відповідно. В останньому прикладі зверніть увагу,$13a^2bc^3$ що еквівалентно$13a^2b^1c^3$, тому додаючи експоненти, ми отримуємо:

\[\begin{aligned} \text { Degree of } 13 a^{2} b c^{3} &=\text { Degree of } 13 a^{2} b^{1} c^{3} \\ &=2+1+3 \\ &=6 \end{aligned} \nonumber \]

Визначення: Мономіальний

Слова мономіальний і термін еквівалентні.

Таким чином,\[-5 \quad-3 x^{2} \quad 12 y^{2} z^{3} \quad 13 a^{2} b c^{3} \nonumber \] є мономи.

Визначення: Біноміальний

Біноміал - це математичний вираз, що містить рівно два члени, розділені знаками плюс або мінус.

Наприклад, кожне з математичних виразів\[2 x+3 y \quad-3 a^{2}-3 b^{2} \quad x y+7 \quad-3 x^{2} y+5 x y^{2} \nonumber \] є біноміальним. Кожен вираз має рівно два члени.

Визначення: Триноміал

Триноміал - це математичний вираз, що містить рівно три члени, розділені знаками плюс або мінус.

Наприклад, кожне з математичних виразів\[2 x^{2}+3 x+7 \quad a^{2}+2 a b+b^{2} \quad x^{4}-2 x^{2} y^{2}+3 y^{4} \nonumber \] є триноміальним. Кожен вираз має рівно три терміни.

Велосипед має два колеса, двочлен - два терміни. Триколісний велосипед має три колеса, триноміал - три терміни. Але як тільки ми пройдемо три терміни, присвоєння спеціальних імен припиняється, і ми використовуємо родове слово polynomial, що означає «багато термінів».

Визначення: Поліном

Многочлен - це багатоіменний математичний вираз, члени розділені знаками плюс або мінус. Коефіцієнти полінома є коефіцієнтами його термінів.

Кожне з попередніх виразів,\[12 y^{2} z^{3} \quad-3 a^{2}-3 b^{2} \quad x^{4}-2 x^{2} y^{2}+3 y^{4} \nonumber \] хоча і присвоєно конкретні імена мономіальні, біноміальні та триноміальні відповідно, також є «багатоіменними» виразами і також можуть називатися поліномами. Однак, оскільки слово поліном означає «багато термінів», ми також можемо використовувати слово поліном для опису математичних виразів з більш ніж трьома термінами, такими як:\[x^{4}-4 x^{3} y+6 x^{2} y^{2}-4 x y^{3}+y^{4} \nonumber \] Коефіцієнти$x^{4}-4 x^{3} y+6 x^{2} y^{2}-4 x y^{3}+y^{4}$ є$1$$−4$,$6$,$−4$, і$1$.

Висхідні та низхідні сили

Коли просять спростити поліноміальний вираз, ми повинні об'єднати будь-які подібні терміни, які ми знаходимо, і, коли це можливо, організувати відповідь у висхідній або спадній силах.

Приклад$\PageIndex{1}$

Спростіть наступний поліноміальний вираз, розташувавши свою відповідь у спадних степенях$x$. Після того, як ви виконали це завдання, зробіть другу домовленість, упорядкувавши свої умови в висхідних силах$x$. \[2 x^{3}+7 x-3 x^{2}+11 x+8 x^{2}+11+15 x \nonumber \]

Рішення

Для того, щоб організувати нашу відповідь у спадних силах$x$, ми хочемо помістити термін з найвищою$x$ силою першого і термін з найменшою силою$x$ останнього. Ми використовуємо комутативні та асоціативні властивості, щоб змінити порядок і перегрупувати, потім об'єднуємо подібні терміни.

\[\begin{aligned} 2 x^{3}+7 x &-3 x^{2}+11 x+8 x^{2}+11+15 x \\ &=2 x^{3}+\left(-3 x^{2}+8 x^{2}\right)+(7 x+11 x+15 x)+11 \\ &=2 x^{3}+5 x^{2}+33 x+11 \end{aligned} \nonumber \]

Зверніть увагу, як повноваження$x$ починаються з$3$, потім опускаються по порядку.

Щоб організувати нашу остаточну відповідь у висхідних силах$x$, ми ставимо найнижчу$x$ силу першої, потім найвищу силу$x$ останнього, перегрупуючи та поєднуючи подібні терміни.

\[\begin{aligned} 2 x^{3}+7 x &-3 x^{2}+11 x+8 x^{2}+11+15 x \\ &=11+(7 x+11 x+15 x)+\left(-3 x^{2}+8 x^{2}\right)+2 x^{3} \\ &=11+33 x+5 x^{2}+2 x^{3} \end{aligned} \nonumber \]

Зверніть увагу, як ми починаємо з постійного терміну, потім повноваження$x$ збільшуються по порядку.

Вправа$\PageIndex{1}$

Спростіть наступний многочлен та організуйте свою відповідь у висхідних силах\[3 x^{2}-5 x^{3}+8 x+9 x^{2}-7 x+2 x^{3} \nonumber \]

Відповідь: $x+12 x^{2}-3 x^{3}$

Коли ми маємо многочлен в одній змінній, наприклад, многочлен у прикладі$\PageIndex{1}$, упорядкування термінів у порядку зростання або спадання є досить простим. Однак многочлен в двох і більше змінних трохи складніше, а іноді і неможливо, розташувати в пристойному порядку.

Приклад$\PageIndex{2}$

Спростіть наступний поліноміальний вираз, а потім організуйте свою відповідь у спадних степенях$x$. \[x^{3}+2 x y^{2}-6 x^{2} y+y^{3}-3 x y^{2}+4 x^{2} y \nonumber \]

Рішення

Ми знову використаємо комутативні та асоціативні властивості, щоб змінити порядок та перегрупувати, поставивши терміни з найвищими повноваженнями$x$ першого, а потім слідуємо термінам, що містять нижчі повноваження$x$ в порядку.

\[\begin{aligned} x^{3}+2 x y^{2} &-6 x^{2} y+y^{3}-3 x y^{2}+4 x^{2} y \\ &=x^{3}+\left(-6 x^{2} y+4 x^{2} y\right)+\left(2 x y^{2}-3 x y^{2}\right)+y^{3} \\ &=x^{3}-2 x^{2} y-x y^{2}+y^{3} \end{aligned} \nonumber \]

Відзначимо, що це дуже природний порядок, повноваження$x$ зменшуються при одночасному$y$ збільшенні повноважень.

Вправа$\PageIndex{2}$

Спростіть наступний многочлен та організуйте свою відповідь у спадних степенях$x$:\[-4 x^{2} y^{2}+3 x y^{3}+6 x^{3} y-x y^{3}+2 x^{2} y^{2} \nonumber \]

Відповідь: $6 x^{3} y-2 x^{2} y^{2}+2 x y^{3}$

Не всі приклади матимуть приємне впорядкування, представлене в прикладі$\PageIndex{2}$, зі степенями однієї змінної за спаданням, тоді як повноваження іншої змінної одночасно зростають. Іноді нам доводиться робити дуже суб'єктивний вибір щодо упорядкування термінів.

Приклад$\PageIndex{3}$

Спростіть наступний поліноміальний вираз, а потім розташуйте свою відповідь у якомусь розумному порядку. \[a^{3} b^{3}+2 a^{2} b-3 a^{2} b^{3}+4 a^{3} b^{3}+5 a^{4}+3 a^{2} b+b^{5} \nonumber \]

Рішення

Спробуємо розташувати терміни так, щоб сили опускалися. Знову ж таки, ми використовуємо комутативні та асоціативні властивості, щоб змінити порядок і перегрупувати.

\[\begin{aligned} a^{3} b^{3}+2 a^{2} b &-3 a^{2} b^{3}+4 a^{3} b^{3}+5 a^{4}+3 a^{2} b+b^{5} \\ &=5 a^{4}+\left(a^{3} b^{3}+4 a^{3} b^{3}\right)+\left(2 a^{2} b+3 a^{2} b\right)-3 a^{2} b^{3}+b^{5} \\ &=5 a^{4}+5 a^{3} b^{3}+5 a^{2} b-3 a^{2} b^{3}+b^{5} \end{aligned} \nonumber \]

Зауважте, що в нашій остаточній домовленості сили$a$ опускаються, але сили$b$ відскакують вгору і вниз, але принаймні ми маємо сили$a$ спадного. Це повинно допомогти нам визначити, якщо ми пропустили термін, спрощуючи дану проблему.

Вправа$\PageIndex{3}$

Спростіть наступний многочлен та організуйте свою відповідь у висхідних силах$b$: \[5 a^{3} b^{2}+4 a b^{3}-2 a^{2} b+3 a^{3} b^{2}-a b^{3} \nonumber \]

Відповідь: $-2 a^{2} b+8 a^{3} b^{2}+3 a b^{3}$

Ступінь многочлена

Щоб знайти ступінь многочлена, знайдіть термін многочлена, що має найвищий ступінь.

Ступінь многочлена

Ступінь многочлена - це ступінь терміна, що має найвищу ступінь.

Знайти ступінь многочлена однієї змінної досить легко.

Приклад$\PageIndex{4}$

Що таке ступінь многочлена$x^{3}-4 x^{2}+5-6 x+2 x^{7}$?

Рішення

Спочатку розставимо многочлен в спадних степенях x.

\[2 x^{7}+x^{3}-4 x^{2}-6 x+5 \nonumber \]

Впорядкування многочлена в спадних ступенях$x$ полегшує побачити, що термін многочлена з найвищим ступенем є$2x^7$. Тому ступінь многочлена є$7$.

Вправа$\PageIndex{4}$

Що таке ступінь многочлена$2 x^{3}+8 x^{2}+3 x^{4}+2 x+10$?

Відповідь: $4$

Знайти ступінь многочлена більше однієї змінної трохи складніше.

Приклад$\PageIndex{5}$

Що таке ступінь многочлена$x^{4}-2 x^{3} y^{7}+y^{5}$?

Рішення

Зверніть увагу, що многочлен вже влаштований у спадних степенях$x$, розташування, яке, ймовірно, так добре, як ми збираємося отримати. У наступній таблиці ми перерахуємо ступінь кожного члена. Пам'ятайте, ступінь будь-якого терміна знаходить шляхом підсумовування показників за його змінними.

\[\begin{array}{cc}{\text { Term }} & {\text { Degree }} \\ \hline x^{4} & {4} \\ {-2 x^{3} y^{7}} & {10} \\ {y^{5}} & {5} \\ \hline\end{array} \nonumber \]

Отже, термін з найвищим ступенем є$-2 x^{3} y^{7}$, роблячи$10$ ступінь многочлена.

Вправа$\PageIndex{5}$

Що таке ступінь многочлена$x^{2} y^{4}-6 x^{2} y^{2}+5 x^{2} y^{5}-2 x y$?

Відповідь: $7$

Функції поліномів

Спочатку ми визначаємо, що ми маємо на увазі під поліноміальною функцією.

Функція полінома

Поліноміальна функція - це функція, визначена правилом, яке присвоює кожному об'єкту області об'єкт діапазону, який визначається поліноміальним виразом.

Просунуті курси, такі як багатовимірне числення, часто використовують поліноміальні функції більш ніж однієї змінної, такі як$f(x, y)=x^{2}+y^{2}$. Однак у цьому курсі наша увага буде зосереджена на поліноміальних функціях однієї змінної, таких як$p(x)=3-4 x-9 x^{2}$ і$q(x)=x^{3}-9 x^{2}+11$.

Приклад$\PageIndex{6}$

Дано поліноміальну функцію$p(x)=x^{3}-8 x-11$, оцініть$p(−3)$.

Рішення

Для оцінки$p(−3)$ спочатку перевстановіть визначення функції, а потім замініть кожне входження змінної$x$ відкритими дужками.

\[\begin{aligned} p(x) &= x^{3}-8 x-11 \quad \color {Red} \text { Original function definition. } \\ p(\;\;) &= (\;\;)^{3}-8(\;\;)-11 \quad \color {Red} \text { Replace each occurrence of } x \text { with open parentheses. } \end{aligned} \nonumber \]

Далі$−3$ підставляємо$x$ в відкриті дужки підготовлені на останньому кроці.

\[\begin{aligned} p(-3) &= (-3)^{3}-8(-3)-11 \quad \color {Red} \text { Substitute }-3 \text { for } x \text { in the open parentheses positions.} \\ p(-3) &= -27-8(-3)-11 \quad \color {Red} \text { Exponent first: }(-3)^{3}=-27 \\ p(-3) &= -27+24-11 \quad \color {Red} \text { Multiply: }-8(-3)=24 \\ p(-3) &= -14 \quad \color {Red} \text { Add. } \end{aligned} \nonumber \]

Отже,$p(−3) = −14$. Ви можете легко перевірити цей результат на своєму калькуляторі (див. Малюнок$\PageIndex{1}$).

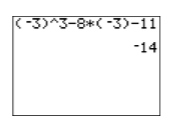
рис. 5.2.1.png — Малюнок$\PageIndex{1}$: Перевірка калькулятора.

Вправа$\PageIndex{6}$

Задано поліноміальну функцію$p(x)=-3 x^{2}+7 x+4$, оцінюємо$p(2)$.

Відповідь: $6$

Графік поліноміальної функції

Однією з найважливіших поліноміальних функцій у всій математиці та науці є поліном, що має ступінь два.

Квадратичний многочлен

Многочлен другого ступеня, що має вигляд,\[p(x)=a x^{2}+b x+c \nonumber \] називається квадратичним многочленом. Графік цього многочлена називається параболою.

Парабола має приблизно П-подібну форму. Деякі відкриваються вгору, деякі відкриваються вниз, в залежності від знака провідного терміна.

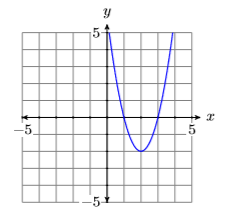
На малюнку$\PageIndex{2}$ провідний термін параболи$p(x)=2 x^{2}-8 x+6$ має позитивні два як коефіцієнт, тому він відкривається вгору.

рис. 5.2.2.png — Малюнок$\PageIndex{2}$: Графік$p(x)=2 x^{2}-8 x+6$ відкриває вгору.

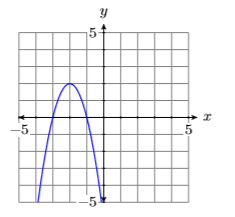
На малюнку$\PageIndex{3}$ провідний термін параболи$p(x)=-2 x^{2}-8 x-6$ має негативні два як коефіцієнт, тому він відкривається вниз.

рис. 5.2.3.png — Малюнок$\PageIndex{3}$: Графік$p(x)=-2 x^{2}-8 x-6$ відкривається вниз.

Примітка

Ознака провідного терміну$p(x)=ax^2 +bx+c$ визначає, чи відкривається парабола вгору або вниз.

Якщо$a>0$, парабола відкривається вгору.
Якщо$a<0$, парабола відкривається вниз.

Переломний момент параболи має особливу назву.

Вершина параболи

Графік многочлена другого ступеня$p(x)=ax^2+bx+c$ має єдину точку повороту, звану вершиною параболи.

Приклад$\PageIndex{7}$

Використовуйте графічний калькулятор, щоб намалювати графік квадратичного многочлена$p(x)=−3x^2 + 12x + 25$.

Рішення

Ступінь многочлена$p(x)=−3x^2 + 12x + 25$ - два, тому це квадратичний многочлен, а його графік - парабола. Більше того, його провідний термін має негативні три як коефіцієнт, тому ми знаємо, що парабола відкривається вниз. Введіть$y = −3x^2 + 12x + 25$ як$Y 1=-3 * X \wedge 2+12 * X+25$ у меню Y = (див. Перше зображення на малюнку$\PageIndex{4}$), потім виберіть 6:ZStandard з меню ZOOM, щоб створити третє зображення на малюнку$\PageIndex{4}$.

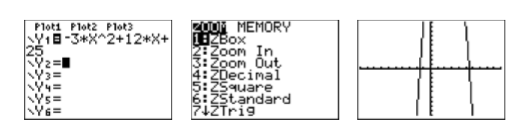
рис. 5.2.4.png — Малюнок$\PageIndex{4}$: Ескіз графіка$p(x)=−3x^2 + 12x + 25$.

Зауважте, що графік$\PageIndex{4}$ на малюнку має U-подібну форму параболи, яка відкривається вниз. Його вершина (поворотна точка) не видно, але можна було б припустити, що вона лежить oу верхній частині екрана. Нам потрібно налаштувати параметри WINDOW так, щоб на екрані перегляду була видна вершина параболи. Після деяких експериментів ми зупинимося на параметрах, показаних на першому зображенні на малюнку$\PageIndex{5}$, а потім натискаємо кнопку GRAPH, щоб створити друге зображення на малюнку$\PageIndex{5}$.

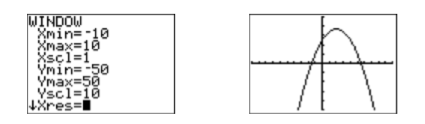
рис. 5.2.5.png — Малюнок$\PageIndex{5}$: Налаштуйте параметри **WINDOW** так, щоб вершина була видимою на екрані перегляду.

Повідомляючи про свій результат на домашнє завдання, дотримуйтесь вказівок щодо подання калькулятора з розділу 3, Розділ 2.

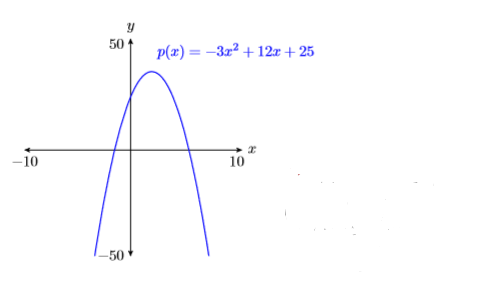
$рис 5.2.5a.png$

Малюємо осі за допомогою лінійки.
Позначте горизонтальну вісь$x$ і вертикальну вісь$y$.
Вкажіть параметри $\mathrm{Xmin}, \mathrm{Xmax}, \mathrm{Ymin}$WINDOW, і$\mathrm{Ymax}$\) в кінці кожної осі.
Від руки криву і позначте її рівнянням.

Вправа$\PageIndex{7}$

Використовуйте ваш графічний калькулятор, щоб намалювати графік квадратичного поліно mial$p(x)=2x^2 −5x−4$.

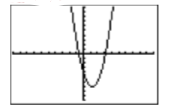
Відповідь: $Колишній 5.2.7.png$

Коли ступінь многочлена більше двох, кількість поворотних точок графіка може збільшуватися. Це робить для деяких дуже цікавих кривих. У більш просунутих курсах, таких як проміжна та коледжська алгебра, ви познайомитеся з різноманітними техніками, які допоможуть вам визначити відповідні вікна перегляду для графіків цих поліномів вищого ступеня. Однак у цьому вступному розділі ми допоможемо вам, запропонувавши гарне оглядове вікно для кожного полінома, таке, яке дозволить вам побачити всі поворотні точки графіка многочлена.

Приклад$\PageIndex{8}$

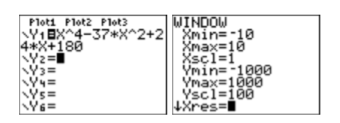
Використовуйте графічний калькулятор, щоб намалювати графік функції полінома$p(x)=x^{4}-37 x^{2}+24 x+180$. Встановіть параметри вікна наступним чином:$\mathbf{X} \min =-10, \mathbf{X} \max =10, \mathbf{X} \operatorname{scl}=1, \mathbf{Y} \min =-1000, \mathbf{Y} \max = 1000,$ і$\mathbf{Y} \operatorname{scl} =100$.

Рішення

Введіть поліноміальну функцію в$\mathbf{Y} \mathbf{1}$ меню Y=, потім введіть запропоновані параметри вікна в меню WINDOW (див. Рис.$\PageIndex{6}$).

рис. 5.2.6.png — Малюнок$\PageIndex{6}$: Введіть многочлен і відрегулюйте параметри WINDOW.

Натисніть кнопку GRAPH у верхньому рядку калькулятора, щоб створити графік функції полінома, показаний на малюнку$\PageIndex{7}$.

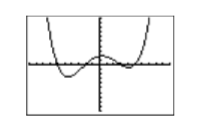
рис. 5.2.7.png — Малюнок$\PageIndex{7}$: Графік$p(x)=x^4 −37x^2 + 24x + 180$.

Солодкий на вигляд крива!

Вправа$\PageIndex{8}$

Скористайтеся вашим графічним калькулятором, щоб намалювати графік квадратичного многочлена p (x) =x3 −14x2 + 20x + 60. Встановіть параметри вікна наступним чином:$\mathbf{X} \min =-10, \mathbf{X} \max =20, \mathbf{X} \operatorname{scl}=1, \mathbf{Y} \min =-200, \mathbf{Y} \max = 200,$ і$\mathbf{Y} \operatorname{scl} =20$.

Відповідь: $Ех 5.2.8.png$