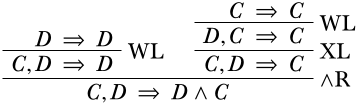8.5: Похідні

Last updated

Oct 27, 2022
Save as PDF
- 8.4: Структурні правила
- 8.6: Приклади похідних

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Template:MathJaxZach

Ми сказали, що початкова послідовність виглядає, і ми дали правила висновку. Похідні в послідовному численні індуктивно генеруються з них: кожне похідне або є початковою послідовністю самостійно, або складається з одного або двох похідних з подальшим висновком.

Визначення $\PageIndex{1}$ : $\Log{LK}$ derivation

A $\Log{LK}$ -похідний послідовності $S$ - це дерево послідовностей, що задовольняють наступним умовам:

Самі верхні послідовності дерева - це початкові послідовності.
Сама нижня послідовність дерева - це $S$ .
Кожна послідовність у дереві крім $S$ є передумовою правильного застосування правила висновку, висновок якого стоїть безпосередньо під цією послідовністю в дереві.

Потім ми говоримо, що $S$ це кінцева послідовність похідного, і $S$ це виводиться в $\Log{LK}$ (або $\Log{LK}$ -derivable).

Приклад $\PageIndex{1}$

Кожна початкова послідовність, наприклад, $C \Sequent C$ є похідною. Ми можемо отримати новий висновок від цього, застосувавши, скажімо, $\LeftR{\Weakening}$ правило,

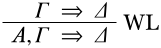
8.5.1.PNG

Правило, однак, має бути загальним: ми можемо замінити $A$ в правилі будь-яким реченням, наприклад, також на $D$ . Якщо передумова відповідає нашій початковій послідовності $C \Sequent C$ , це означає, що $\Delta$ обидва $\Gamma$ і справедливі $C$ , і висновок буде тоді $D, C \Sequent C$ . Отже, наступне - це деривація:

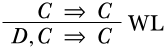
8.5.2.png

Тепер ми можемо застосувати інше правило $\LeftR{\Exchange}$ , скажімо, яке дозволяє нам змінити два речення зліва. Отже, наступне також є правильним виведенням:

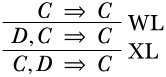
8.5.3.png

При цьому застосовується правило, яке було дано як

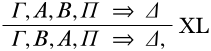
8.5.4.png

обидва $\Gamma$ і $\Pi$ були порожніми $C$ , $\Delta$ є, і ролі $A$ і $B$ грають $D$ і $C$ , відповідно. Багато в чому так само ми також бачимо, що

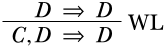
8.5.5.png

це деривація. Тепер ми можемо взяти ці два похідні, і об'єднати їх за допомогою $\RightR{\land}$ . Це правило було

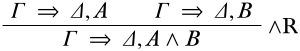
8.5.6.png

У нашому випадку приміщення повинно збігатися з останніми послідовністю похідних, що закінчуються в приміщеннях. Це означає, що $\Gamma$ $\Delta$ є $C, D$ , порожній, $A$ є $C$ і $B$ є $D$ . Отже, висновок, якщо висновок повинен бути правильним, є $C, D \Sequent C \land D$ .

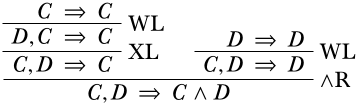
8.5.7.png

Звичайно, ми також можемо змінити приміщення, тоді $A$ було б $D$ і $B$ було б $C$ .

8.5.8.png