8.6: Приклади похідних

Last updated
Save as PDF

Page ID: 52945

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Template:MathJaxZach

Приклад\(\PageIndex{1}\)

Дайте\(\Log{LK}\) -деривацію для послідовності\(A \land B \Sequent A\).

Починаємо з написання потрібної кінцевої послідовності внизу деривації.

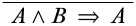
8.6.1.png

Далі нам потрібно розібратися, який висновок може мати нижчу послідовність цієї форми. Це може бути структурним правилом, але непогано почати з пошуку логічного правила. Єдина логічна сполучна, що відбувається в нижній послідовності\(\land\), так що ми шукаємо\(\land\) правило, і так як\(\land\) символ відбувається в попередньому, ми дивимося на\(\LeftR{\land}\) правило.

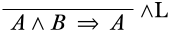
8.6.2.png

Є два варіанти того, що могло бути верхньою послідовністю\(\LeftR{\land}\) висновку: ми могли б мати верхню послідовність\(A \Sequent A\), або з\(B \Sequent A\). Зрозуміло, що\(A \Sequent A\) це початкова послідовність (що є хорошою справою), хоча\(B \Sequent A\) взагалі не виводиться. Заповнюємо верхню послідовність:

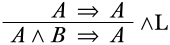
8.6.3.png

Тепер у нас є правильне\(\Log{LK}\) -виведення послідовності\(A \land B \Sequent A\).

Приклад\(\PageIndex{2}\)

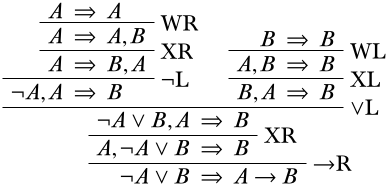
Дайте\(\Log{LK}\) -деривацію для послідовності\(\lnot A \lor B \Sequent A \lif B\).

Почніть з написання потрібної кінцевої послідовності внизу деривації.

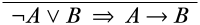
8.6.4.png

Щоб знайти логічне правило, яке могло б дати нам цю кінцеву послідовність, ми розглянемо логічні зв'язки в кінцевій послідовності:\(\lnot\),\(\lor\), і\(\lif\). На даний момент ми дбаємо лише про те\(\lor\),\(\lif\) що вони є основними операторами речень у кінцевій послідовності, перебуваючи\(\lnot\) в межах іншої сполучної, тому ми подбаємо про це пізніше. Отже, наші варіанти логічних правил для остаточного висновку є\(\LeftR{\lor}\) правилом і\(\RightR{\lif}\) правилом. Ми могли б вибрати будь-яке правило, насправді, але давайте виберемо\(\RightR{\lif}\) правило (якщо ні з якої іншої причини, ніж це дозволяє нам відкласти поділ на дві гілки). Відповідно до форми\(\RightR{\lif}\) висновків, які можуть дати нижню послідовність, це повинно виглядати так:

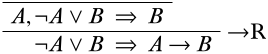
8.6.5.png

Якщо ми перейдемо\(\lnot A \lor B\) до зовнішньої частини попередньої частини, ми можемо застосувати\(\LeftR{\lor}\) правило. Згідно зі схемою, це повинно розбиватися на дві верхні послідовності наступним чином:

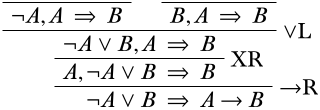
8.6.6.png

Пам'ятайте, що ми намагаємося накрутити свій шлях до початкових послідовностей; ми, здається, досить близько! Правильна гілка - це лише одне ослаблення та один обмін від початкової послідовності, а потім це робиться:

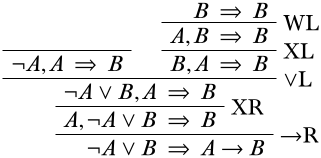
8.6.7.png

Тепер, дивлячись на ліву гілку, єдиним логічним сполучним у будь-якому реченні є\(\lnot\) символ у попередніх реченнях, тому ми дивимося на екземпляр\(\LeftR{\lnot}\) правила.

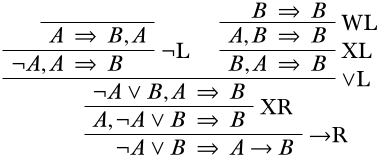
8.6.8.png

Подібно до того, як ми закінчили праву гілку, ми лише один ослаблення і один обмін від закінчення цієї лівої гілки, а також.

8.6.9.png

Приклад\(\PageIndex{3}\)

Дайте\(\Log{LK}\) -деривацію послідовності\(\lnot A \lor \lnot B \Sequent \lnot (A \land B)\)

Використовуючи прийоми зверху, починаємо з написання потрібної кінцевої послідовності внизу.

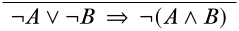
8.6.10.пнг

Доступними основними зв'язками речень в кінцевій послідовності є\(\lor\) символ і\(\lnot\) символ. Було б працювати, щоб застосувати\(\LeftR{\lor}\) або\(\RightR{\lnot}\) правило тут, але ми починаємо з\(\RightR{\lnot}\) правила, оскільки воно дозволяє уникнути поділу на дві гілки на мить:

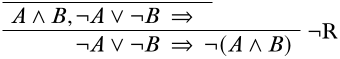
8.6.11.пнг

Тепер у нас є вибір, чи варто дивитися на\(\LeftR{\lor}\) правило\(\LeftR{\land}\) або. Давайте подивимося, що відбувається, коли ми застосовуємо\(\LeftR{\land}\) правило: у нас є вибір почати або з послідовності,\(A, \lnot A \lor B \Sequent \quad\) або з послідовності\(B, \lnot A \lor B \Sequent \quad\). Оскільки доказ симетричний щодо\(A\) і\(B\), давайте перейдемо до першого:

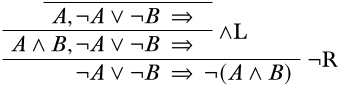
8.6.12.пнг

Продовжуючи заповнювати деривацію, ми бачимо, що стикаємося з проблемою:

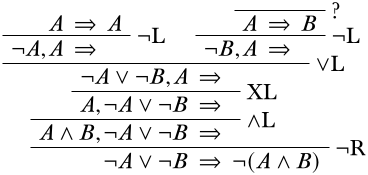
8.6.13.пнг

Верхня частина правої гілки не може бути зменшена далі, і вона не може бути доведена шляхом структурних висновків до початкової послідовності, тому це не правильний шлях. Тож очевидно, що було помилкою застосовувати наведене вище\(\LeftR{\land}\) правило. Повертаючись до того, що ми мали раніше, і виконуючи\(\LeftR{\lor}\) правило замість цього, ми отримуємо

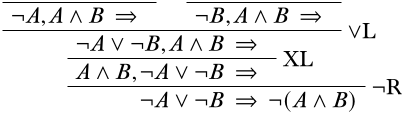
8.6.14.пнг

Заповнюючи кожну гілку, як ми робили раніше, отримуємо

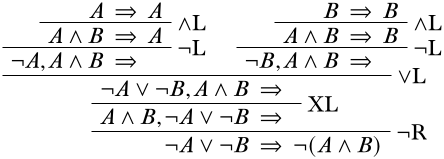
8.6.15 пнг

(Ми могли б виконати\(\land\) правила нижче, ніж\(\lnot\) правила на цих кроках, і все одно отримали правильну деривацію).

Приклад\(\PageIndex{4}\)

Поки що ми не використовували правило скорочення, але іноді це потрібно. Ось приклад, де це відбувається. Припустимо, ми хочемо довести\(\quad \Sequent A \lor \lnot A\). Застосування\(\RightR{\lor}\) назад дасть нам одне з цих двох похідних:

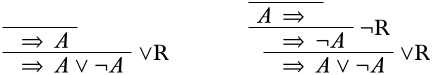
8.6.16 пнг

Жодне з них, звичайно, не закінчується початковою послідовністю. Хитрість полягає в тому, щоб зрозуміти, що правило скорочення дозволяє нам об'єднати дві копії речення в одну - і коли ми шукаємо докази, тобто, йдучи знизу вгору, ми можемо зберегти копію\(A \lor \lnot A\) в приміщенні, наприклад,

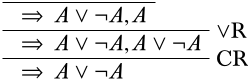
8.6.17 пнг

Тепер ми можемо подати\(\RightR{\lor}\) заявку вдруге, а також отримати\(\lnot A\), що призводить до повного виведення.

8.6.18 пнг

Проблема\(\PageIndex{1}\)

Наведіть похідні наступних послідовностей:

\(\Sequent \lnot(A \lif B) \lif (A \land \lnot B)\)
\((A \land B) \lif C \Sequent (A \lif C) \lor (B \lif C)\)