4.5: Рівняння руху Ейлера

У нашому першому вступі до класичної механіки ми дізнаємося, що коли зовнішній крутний момент діє на тіло, його кутовий момент змінюється (і якщо зовнішні крутні моменти не діють на тіло, його кутовий момент не змінюється). Дізнаємося, що швидкість зміни моменту моменту дорівнює прикладеному крутному моменту. У перших простих прикладах, які ми зазвичай зустрічаємо, симетричне тіло обертається навколо осі симетрії, і крутний момент також застосовується навколо цієї ж осі. Кутовий імпульс просто$I\omega$, і тому твердження, що крутний момент дорівнює швидкості зміни моменту імпульсу просто,$\tau = I \dot{\omega}$ і це все, що є до нього.

Пізніше дізнаємося$I \boldsymbol\omega$, що$\bf{L}$ =, де$\bf{l}$ тензор,$\bf{L}$ а$\boldsymbol\omega$ не паралельні. Є три основні моменти інерції, і$\bf{L}$,$\boldsymbol\omega$ і прикладається крутний момент$\boldsymbol\tau$ кожен має три складові, і твердження «крутний момент дорівнює швидкості зміни моменту моменту» якось стає набагато менш легким.

Рівняння Ейлера розібратися в цьому, і дати нам зв'язок між складовими$\boldsymbol\tau$,$\bf{l}$ і$\boldsymbol\omega$.

Для малюнка IV.5 я щойно відтворив, з деякими невеликими модифікаціями, малюнок III.19 з моїх заміток на цьому веб-сайті про небесну механіку, де я визначив кути Ейлера. Знову пропонується, щоб ті, хто не знайомий з Ейлерівськими кутами, проконсультувалися з главою III Небесної Механіки.

На малюнку IV.5$Oxyz$ - це осі, закріплені на просторі, і$Ox_{0}y_{0}z_{0}$ є основними осями, закріпленими на тілі. Вісь$Oy_{0}$ знаходиться за площиною вашого екрану; вам доведеться заглянути всередину монітора, щоб знайти його.

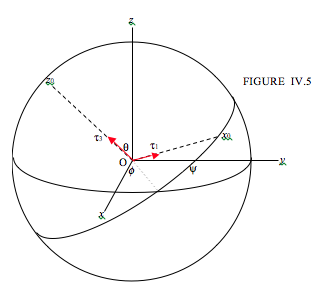
Я припускаю, що зовнішній крутний момент$\boldsymbol\tau$ діє на корпус, і я намалював компоненти$\tau_{1}$ і$\tau_{3}$. Тепер припустимо, що тіло обертається таким чином, щоб кут Ейлера$\psi$ мав збільшитися на$\delta\psi$. Думаю, буде з готовністю домовлено, що робота, виконана над тілом, є$\tau_{3}\delta\psi$. Це означає, слідуючи нашому визначенню узагальненої сили в розділі 4.4,$\tau_{3}$ тобто узагальнена сила, пов'язана з узагальненою координатою$\psi$. Встановивши, що тепер ми можемо застосувати рівняння Лагранжа 4.4.1:

$$\ \frac{\text{d}}{\text{d}t} (\frac{\partial T}{\partial \dot{\psi}})-\frac{\partial T}{\partial \psi} = \tau_{3} \tag{4.5.1}\label{eq:4.5.1}$$

Тут кінетична енергія - це вираз, який ми вже встановили в Рівнянні 4.3.6. Незважаючи на дещо страшний аспект Equation 4.3.6, до нього досить легко$\ref{eq:4.5.1}$ застосувати рівняння. Таким чином

$$\ \frac{\partial T}{\partial \dot{\psi}}= I_{3}(\dot{\phi}cos\theta + \psi) = I_{3}\omega \tag{4.5.2}\label{eq:4.5.2}$$

де я скористався рівнянням 4.2.3.

Тому

$$\ \frac{\text{d}}{\text{d}t}(\frac{\partial T}{\partial \dot{\psi}}) = I_{3}\dot{\omega_{3}} \tag{4.5.3}\label{eq:4.5.3}$$

І, якщо ми скористаємося рівняннями 4.2.1,2,3, це легко отримати

$$\ \frac{\partial T}{\partial \psi}) = I_{1}\omega_{1}\omega_{2}- I_{2}\omega_{2}\omega_{2} = \omega_{1}\omega_{2}(I_{1}-I_{2}) \tag{4.5.4}\label{eq:4.5.4}$$

Таким чином Рівняння$\ref{eq:4.5.1}$ стає:

$$\ I_{3}\dot{\omega_{3}} - (I_{1} -I_{2})\omega_{1}\omega_{1} = \tau_{3} \tag{4.5.5}\label{eq:4.5.5}$$

Це одне з рівнянь руху Ейлера.

Тепер, хоча ми побачили, що$\tau_{3}$ це узагальнена сила, пов'язана з координатою y, нам буде однаково ясно, що$\tau_{1}$ це не узагальнена сила, пов'язана з q, а також не узагальнена сила, пов'язана з$\phi$.$\tau_{2}$ Однак нам не потрібно думати про те, що таке узагальнені сили, пов'язані з цими двома координатами; це набагато простіше, ніж це. Щоб отримати інші два рівняння Ейлера, все, що потрібно, - це здійснити циклічну перестановку індекси в Рівнянні$\ref{eq:4.5.5}$. Таким чином, три рівняння Ейлера:

$$\ I_{1}\dot{\omega_{1}} - (I_{2}-I_{2})\omega_{2}\omega_{3} = \tau_{1} , \tag{4.5.6}\label{eq:4.5.6}$$

$$\ I_{2}\dot{\omega_{2}} - (I_{3}-I_{1})\omega_{3}\omega_{1} = \tau_{2} , \tag{4.5.7}\label{eq:4.5.7}$$

$$\ I_{3}\dot{\omega_{3}} - (I_{1}-I_{2})\omega_{1}\omega_{2} = \tau_{3} . \tag{4.5.8}\label{eq:4.5.8}$$

Вони займають місце, з$\tau = I \dot{\omega}$ якими ми більше знайомі в елементарних задачах, в яких тіло обертається навколо головної осі і крутний момент застосовується навколо цієї головної осі.

Якщо зовнішніх крутних моментів, що діють на тіло, то маємо Рівняння Ейлера вільного обертання жорсткого тіла:

$$\ I_{1}\dot{\omega_{1}} = (I_{2}-I_{3})\omega_{2}\omega_{3} , \tag{4.5.9}\label{eq:4.5.9}$$

$$\ I_{1}\dot{\omega_{2}} = (I_{3}-I_{1})\omega_{3}\omega_{1} , \tag{4.5.10}\label{eq:4.5.10}$$

$$\ I_{3}\dot{\omega_{3}} = (I_{1}-I_{2})\omega_{1}\omega_{2} . \tag{4.5.11}\label{eq:4.5.11}$$

Приклад$\PageIndex{1}$

На наведеному вище кресленні прямокутна пластинка обертається з постійною кутовою швидкістю$\boldsymbol\omega$ між двома підшипниками без тертя. Ми збираємося застосувати до нього рівняння руху Ейлера. Ми виявимо, що підшипники чинять крутний момент на прямокутник, а прямокутник надає крутний момент на підшипники. Кутовий момент прямокутника не є постійним — принаймні він не постійний у напрямку. Розрахуємо крутний момент (його величину і напрямок) і подивимося, що відбувається з моментом.

Відзначимо, що основними (другими) моментами інерції є

$I_{1} = \frac{1}{3}mb^{2} \qquad I_{2} = \frac{1}{3}ma^{2} \qquad I_{3} = \frac{1}{3}m(a^{2} +b^{2})$

і що складовими кутової швидкості є

$\omega_{1} = \omega \cos \theta \qquad \omega_{2} = \omega \sin \theta \qquad \omega_{3} = 0.$

Також$\dot{\boldsymbol\omega}$ і всі його складові нульові. Ми відразу отримуємо, з рівнянь Ейлера, що$\tau_{1}$ і$\tau_{2}$ дорівнює нулю, і що крутний момент, що чиниться на прямокутник підшипниками, є

$\tau_{3} = (I_{2}-I_{1})\omega_{1}\omega_{2} = \frac{1}{3}m(a^{2}-b^{2})\omega^{2}sin \theta \cos \theta$

І з тих пір

$\sin \theta = \frac{b}{\sqrt{a^{2} +b^{2}}} \quad and \quad \cos \theta = \frac{b}{\sqrt{a^{2} +b^{2}}},$

отримуємо

$\tau_{3} = \frac{m(a^{2} - b^{2})ab}{3(a^{2} + b^{2})}\omega^{2}$

Таким чином$\boldsymbol\tau$, крутний момент, що чиниться на прямокутник підшипниками, спрямований в нормаль до площини прямокутника (з площини паперу в миттєвому знімку вище).

Кутовий імпульс задається${ \bf L} = {\bf l} \boldsymbol\omega$. Тобто сказати:

$\left(\begin{array}{c}L_{1}\\ L_{2}\\L_{3}\end{array}\right) = \frac{1}{3}m\left(\begin{array}{c}b^{2} \quad 0 \quad 0\\ 0 \quad a^{2} \quad 0 \\ 0 \quad 0 \quad a^{2}+b^{2}\end{array}\right)\left(\begin{array}{c}\omega \cos \theta\\ \omega \sin \theta \\ 0\end{array}\right)$

$L_{1} = \frac{1}{3}mb^{2}\omega \cos \theta = \frac{1}{3}m\frac{ab^{2}}{\sqrt{a^{2}+b^{2}}}\omega$

$L_{2} = \frac{1}{3}mb^{2}\omega \sin \theta = \frac{1}{3}m\frac{ab^{2}}{\sqrt{a^{2}+b^{2}}}\omega$

$L_{3} = 0$

$L = \frac{1}{3} mab \omega$

$L_{2}/ L_{1} = \frac{a^{2}sin \theta}{b^{2}cos \theta} = \cot \theta = tan(90° - \theta)$

Це говорить нам про те, що$\bf L$ знаходиться в площині прямокутника, і робить кут 90° -$\theta$ з$x$ -віссю, або q з$y$ -віссю, і він обертається навколо вектора$\boldsymbol\tau$. $\boldsymbol\tau$перпендикулярно площині прямокутника, і, звичайно, зміна$\bf L$ відбувається в цьому напрямку. Крутний момент не працює,$\boldsymbol\omega$ а$T$ є постійними. Читач може знайти аналогію в ситуації планети на орбіті навколо Сонця по круговій орбіті.. Планета відчуває силу, яка завжди перпендикулярна її швидкості. Сила не працює, а швидкість і кінетична енергія залишаються постійними.

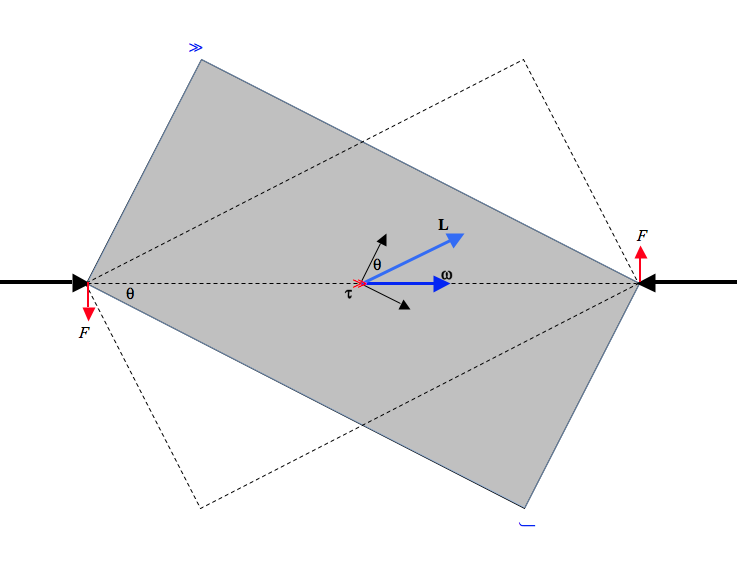
Крутний момент на пластині можна представити як пару сил, що чиниться підшипниками на пластині, кожна величини$\frac{\tau_{3}}{2\sqrt{a^{2} + b^{2}}},$ або$\frac{m(a^{2}-b^{2})}{6(a^{2}-b^{2})^\frac{3}{2}}\omega^{2}$ сили, що чиниться пластиною на підшипники, знаходяться, звичайно, у зворотному напрямку.

Приклад$\PageIndex{2}$

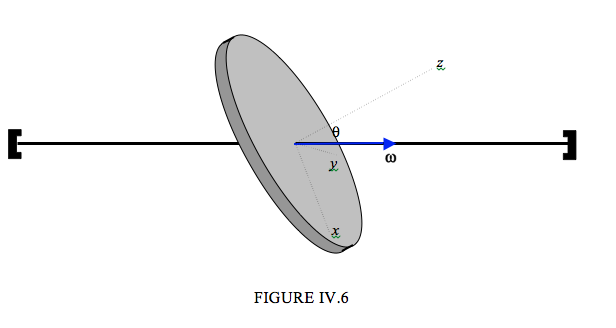
На малюнку IV.6 зображений диск маси$m$, радіусом$a$, що обертається з постійною кутовою швидкістю$\omega$ близько біля осі, яка нахилена під кутом$\theta$ до нормалі до диска. Я намалював три основні осі, зафіксовані тілом. Осі$x$ - і$y$ - знаходяться в площині диска\ жирним шрифтом; напрямок$x$ -осі вибирається так, щоб вісь (а значить і вектор$\boldsymbol\omega$) знаходилася в$zx$ -площині. Диск, очевидно, незбалансований, і на ньому повинен бути крутний момент, щоб підтримувати рух.

$\boldsymbol\omega$Оскільки постійна, всі компоненти$\dot{ \boldsymbol\omega}$ нульові, так що рівняння Ейлера є

$\tau_{1}= (I_{3} - I_{2})\omega_{3}\omega_{2},$

$\tau_{2}= (I_{1} - I_{3})\omega_{1}\omega_{3},$

$\tau_{3}= (I_{2} - I_{1})\omega_{2}\omega_{1},$

Зараз$\omega_{1} = \omega \sin \theta , \omega_{2} = \omega \cos \theta , I_{1} = \frac{1}{4} ma^{2} , I_{2} = \frac{1}{4} ma^{2}, I_{3} = \frac{1}{1} ma^{2}$

Тому$\tau_{1} = \tau_{3} = 0, and \tau_{2} = - \frac{1}{4}ma^{2}\omega ^{2}sin\theta cos\theta = -\frac{1}{8}ma^{2}\omega^{2}sin2\theta$

(Перевірте, як завжди, чи цей вираз є правильним за розмірами.) При цьому крутний момент, що діє на диск, знаходиться в$y$ негативному -напрямку.

Чи можете ви змирити той факт, що діє на диск крутний момент з тим, що він рухається з постійною кутовою швидкістю? Так, найрішучіше! Що не є постійним, так це кутовий імпульс$\bf{L}$, який рухається навколо осі в конусі такий$\dot{\bf L} = -\tau_{2} { \bf j}$, що, де$\bf{j}$ блок вектор вздовж$y$ -осі.