6.3: Ковектор частотно-хвильового числа

Last updated
Save as PDF

Page ID: 77291

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

\(\omega \to \)Вивчення частотно-хвильового ковектора

Узагальнюючи від\(0 + 1\) розмірів до\(3 + 1\), ми могли б мати спостерігача, що рухається інерційно вздовж вектора швидкості\(\to o\), підраховуючи фазу\(φ\) (в радіанах) плоскої хвилі (можливо, водяної хвилі або електромагнітної хвилі), яка омиває над нею. Оскільки\(φ\) це просто підрахунок, то це явно скаляр. Це означає, що у нас є якась функція, яка приймає як вхід вектор\(\to o\) і дає як вихід скаляр\(φ\). Ця функція має всі правильні характеристики, які слід описати як вимірювання\(ω\to o\)\(\to o\) з деяким ковектором\(ω\to \), і в конструктивному стилі математики це хороший спосіб визначення ковектора: це лінійна функція від простору векторів до дійсних чисел. Ми\(ω\to \) називаємо частотно-хвильовим ковектором, або просто частотним ковектором для короткого. Якщо\(\to o\) представляє одну секунду, виміряну на годиннику цього спостерігача, то\(ω\to o\) це частота,\(ω\) виміряна цим спостерігачем в одиницях радіанів в секунду. Якщо ж спостерігач вважає\(s\) вектором одночасності з довжиною в один метр, то\(ω\to s\) відбувається вимір спостерігачем хвильового числа\(k\), визначеного як\(2π\) поділене на довжину хвилі.

Візуалізація

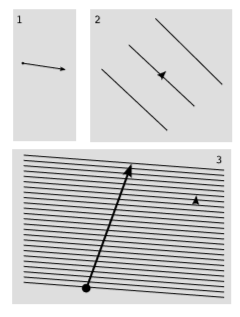
рис. 6.3.1.png — Малюнок\(\PageIndex{1}\): 1. Вектор зміщення 2. Ковектор 3. Вимірювання зводиться до підрахунку. Спостерігач, представлений вектором зміщення, підраховує 24 хвильових фронту.

У більш ніж одному вимірі існують природні способи візуалізації різних векторних просторів, населених векторами та ковекторами. Вектор - це стрілка. Ковектор може бути візуалізований як набір паралельних, рівномірно розташованих ліній на топографічній карті,\(\PageIndex{1}\) (2), зі стрілкою, щоб показати, який шлях «в гору». Акт вимірювання складається з підрахунку того, скільки з цих ліній перетинається певним вектором, малюнком\(\PageIndex{1}\) (3).

Приклад\(\PageIndex{1}\): Parallelism between vectors and covectors

На малюнку\(\PageIndex{1}\) (3) здається візуально очевидним, що вектор і ковектор майже, але не точно, паралельні, так як стрілки вказують практично в одному напрямку. Зазвичай паралелізм ненульових векторів\(u\) і виражався\(v\) б існуванням дійсного числа\(α\) такого, що\(u = αv\). Але вектори і ковектори - це різні види звірів, що належать до різних векторних просторів. Масштабування зебри ніколи не дасть жирафа. Якщо метрики немає, то це просто факт життя: немає природного способу визначити паралелізм між вектором\(v\) і ковектором\(ω\).

Але якщо у нас є метрика, то ми можемо визначити величину для vectorc на малюнку\(\PageIndex{1}\) (3), і зберегти цю величину постійною під час обертання\(v\). Якщо метрика евклідова, то це відповідає жорсткому обертанню стрілки на сторінці, і\(ω\to v\) максимізується для певної орієнтації, яку ми визначаємо як умову паралелізму. Якщо метрика неевклідова, то речі стають трохи складнішими, але ті ж ідеї застосовуються, якщо вектори або просторові, або обидва часові. Наприклад, якщо обидва є схожими на час, то\(ω\to v\) мінімізується паралелізмом, оскільки нерівність Коші-Шварца зворотна (див. Розділ 1.5)

Градієнт

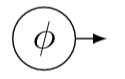
Задано скалярне поле\(φ\), його градієнт\(∇φ\) у будь-якій заданій точці є ковектором. Частотний ковектор - це градієнт фази. У позначеннях birdtracks ми вказуємо це, написавши його стрілкою, спрямованою назовні,\((∇φ)\). Оскільки градієнти трапляються так часто, позначення birdtracks має спеціальне скорочення для них, яке є просто колом:

рис. 6.3.2.png

Це позначення також може бути розширено на випадок, коли річ, що диференціюється, не є скалярною, але тоді виникають деякі ускладнення, коли координати не Мінковський; див. Розділ 9.4.

Приклад\(\PageIndex{2}\): Cosmological observers

Час відносний, так що ж мають на увазі люди, коли кажуть, що Всесвіту\(13.8\) мільярд років? Якби гіпотетичний спостерігач був навколо незабаром після великого вибуху, час, що минув на годиннику цього спостерігача, залежатиме від світової лінії спостерігача. Два таких спостерігача, які мали різні світові лінії, могли мати різні показання годин.

Сучасні космологи не наївні щодо розширення часу. Вони мають на увазі космологічно кращу світову лінію для свого спостерігача. Один із способів побудови цієї світової лінії полягає в наступному. Згодом температура\(T\) Всесвіту знизилася. (Ми визначаємо цю температуру локально, але ми середні показники по досить великих регіонах, щоб місцеві варіації не мали значення.) Негативний градієнт цієї температури є ковектором\(-∇T\), який вказує у бажаному напрямку в просторово-часі, а кращою світовою лінією для спостерігача є той, вектор\(v\) швидкості якого завжди паралельний\(-∇T\), у сенсі, визначеному в прикладі\(\PageIndex{1}\) вище.