6.6: Фазова та групова швидкість

Last updated
Save as PDF

Page ID: 77275

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Поясніть фазову швидкість і групову швидкість

Фазова швидкість

Хвильовий фронт - це лінія або поверхня постійної фази. У знімку хвилі в один момент часу напрямок поширення хвилі - поперек хвильових фронтів. Візуальна ситуація відрізняється на просторово-часовій діаграмі.

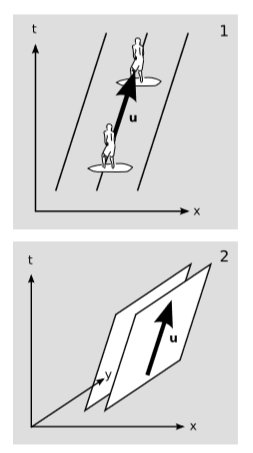
рис. 6.6.1.png — Малюнок\(\PageIndex{1}\): Серфер рухається прямо вправо з вектором швидкості\(u\). Хвиля також поширюється вправо.

У\(1 + 1\) розмірах, малюнок\(\PageIndex{1}\) (1), припустимо, що лінії представляють гребінь водних хвиль. Серфер знаходиться на вершині гребеня, їде разом з ним. Його вектор швидкості\(u\) знаходиться в напрямку просторовогочасу, який лежить на вершині хвильового фронту, а не поперек нього. Очевидно, що і його рух, і поширення хвилі знаходяться праворуч, а не ліворуч, як ми могли собі уявити, грунтуючись на досвіді зі знімками хвиль.

У\(2+1\) розмірах\(\PageIndex{1}\) (2) швидкість серфера візуалізується як стрілка, що лежить в площині постійної фази. Враховуючи фазову інформацію хвилі, існує більше однієї можливої стрілки такого роду. Ми могли б спробувати вирішити неоднозначність, вимагаючи, щоб проекція стрілки в\(xy\) площину була перпендикулярна перетину хвильових фронтів з цією площиною, але (за винятком випадку, коли хвиля рухається на\(c\), Приклад\(\PageIndex{1}\)) цей рецепт дає результати, які змінюються залежно від нашої системи відліку, і зміни не описуються перетворенням Лоренца вектора швидкості. Це показує, що в загальному випадку фазова інформація хвилі, закодована в частотному ковекторі\(ω\to \), не описує напрямок поширення хвилі через простір. У більшості випадків це говорить нам про фазову швидкість хвилі\(ω/k\), яка насправді не є швидкістю. Все це симптоми того, що швидкість повинна бути вектором, але\(ω\to \) є ковектором. Фазової швидкості не вистачає фізичного інтересу, оскільки це не швидкість, з якою рухається будь-яка «штучка».

Вектор швидкості світлової хвилі з урахуванням її фази

Ми бачили, що загалом інформація про фазу хвилі, закодованої в,\(ω\to \) не визначає її напрямок поширення. Виняток становить хвиля, така як світлова хвиля, яка поширюється при\(c\). Нехай світова лінія поширення хвилі лежить вздовж вектора\(\to v\). У випадку хвилі, що поширюється на\(c\), ми маємо\(v^2 = 0\) (так що не\(\to v\) може мати звичайну нормалізацію для вектора швидкості), і співвідношення дисперсії просто\(ω^2 = 0\). Оскільки фаза залишається постійною вздовж світової лінії поширення,\(ω\to v = 0\). Тому ми знаходимо, що\(v\) і\(ω\) є двома ненульовими, світлоподібними векторами, ортогональними один до одного. Але як показано в задачі Q10 в главі 1, це означає, що два вектори паралельні. Таким чином, якщо нам дано ковектор\(ω\to \), ми просто повинні обчислити його подвійний,\(\to ω\) щоб знайти напрямок поширення.

Групова швидкість

Фазова швидкість - це не та швидкість, з якою «матеріал» передається хвилею. Швидкість матеріалу називається груповою швидкістю. Щоб мати змістовно визначену групову швидкість, нам потрібно мати хвилю, яка модулюється, оскільки немодульована хвиля - це нескінченна синусоїда, яка тягнеться до нескінченності, і така немодульована хвиля не передає жодної енергії чи інформації. Немодульована хвиля має однаковий частотний ковектор\(ω\to \) протягом усього простору-часу, тобто однакову частоту\(ω\) і хвильове число\(k\). Одним із способів опису модульованої хвилі є те, як\(ω\to \) змінюється.

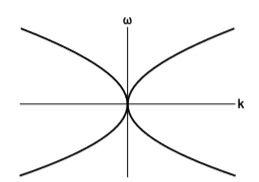
рис. 6.6.2.png — Малюнок\(\PageIndex{2}\): Точки на графіку задовольняють дисперсійному співвідношенню\(C = 0\) для водних хвиль. У даній точці на графіку ковектор\((∇C)\) повідомляє нам групову швидкість.

Але різні компоненти не вільні змінювати будь-яким випадково обраним способом.\(ω\to \) Зазвичай вони обмежені дисперсійним співвідношенням. Наприклад, поверхневі хвилі в глибокій воді підкоряються обмеженню\(C = 0\), де\(C = ω^4 - α^2k^2\) (фігура\(\PageIndex{2}\)) і\(α\) є постійною з одиницями прискорення, що відноситься до прискорення сили тяжіння. (Оскільки вода нескінченно глибока, немає іншої шкали, яка могла б увійти в обмеження.)

Тепер, якщо певний удар на конверті, з яким хвиля модулюється відвідує події простору часу\(P\) і\(Q\), то незалежно від частоти та довжини хвилі хвиля біля шишки спостерігаються однаковими при\(P\) і\(Q\). Загалом,\(k\) і\(ω\) є постійними вздовж просторучасу зміщення будь-якої точки на конверті, тому зміщення простору/часу\(\to r\) від\(P\) до\(Q\) має задовольняти умові\((∇ω)\to r = 0\).

Крім того,\(∇ω\) повинна бути дотичною до поверхні обмеження\(C = 0\), щоб хвиля завжди підкорялася обмеженню. Таким чином, з огляду на точку\(ω\to \) в частотному просторі, напрямок поширення\(r\) має бути однозначно визначено обмеженням. Припустимо,\(C\) це добре поведена функція, так що це приблизно лінійна функція будь-якого невеликого зміни\(∆ω\), тобто в\(1 + 1\) розмірах ми маємо

\[\Delta C = \frac{\partial C}{\partial \omega }\Delta \omega + \frac{\partial C}{\partial k}\Delta k\]

У цьому наближенні\(∆C\) є лінійна функція, яка діє на ковектор\(∆ω\) і повертає скаляр. Іншими словами,\(∆C\) діє як вектор з компонентами

\[\Delta C = \left ( \frac{\partial C}{\partial \omega }, \frac{\partial C}{\partial k} \right )\]

Цей вектор паралельний\(r\), так що він вказує у напрямку поширення хвилі через просторовий час і повідомляє нам свою групову швидкість\(\left ( \tfrac{\partial C}{\partial k} \right )/ \left ( \tfrac{\partial C}{\partial \omega } \right )\). У нашому прикладі водних хвиль розрахунок показує, що групова швидкість\(±α/2ω\) дорівнює половині фазової швидкості.