6.5: Доплерівський зсув і аберація
- Page ID
- 77284
Цілі навчання
- Що таке аберація
доплерівські зрушення
Як приклад ми узагальнюємо наше попереднє обговорення доплерівського зсуву світла до\(3 + 1\) розмірів.
Для наочності, давайте спочатку покажемо, як працює\(1+1\) -мірний випадок в нашій новій нотації. Для хвилі, що йде вліво, ми маємо\(ω\to = (ω,ω)\) (немає\((ω,-ω)\) — див. Рис. 6.6.1 (1). Тепер ми хочемо трансформуватися в кадр спостерігача, що рухається вправо зі швидкістю\(v\) відносно вихідного кадру. Оскільки\(ω\to \) це ковектор, ми робимо це за допомогою зворотного перетворення Лоренца. Звичайне перетворення Лоренца прийме світлоподібний вектор\((ω,ω)\)\((ω/D,ω/D)\) (див. Розділ 3.2). Зворотне перетворення Лоренца дає\((Dω,Dω)\). Частота була зрушена вгору на коефіцієнт\(D\), як було встановлено раніше.
У\(3 + 1\) розмірах просторова площина визначається напрямком поширення світла і відносною швидкістю джерела і спостерігача, тому цей випадок зводиться без втрати спільності до\(2 + 1\) розмірів. Частота чотиривекторна повинна бути світлоподібною, тому її найбільш загальною можливою формою\(θ\) є\((ω,ω cosθ,ω sinθ)\), де інтерпретується як кут між напрямком поширення і відносною швидкістю. У\(2+1\) розмірах поштовх Лоренца вздовж\(x\) - осі виглядає так:
\[t' = \gamma t - v\gamma x\]
\[x' = - v\gamma t + \gamma x\]
\[y' = y\]
Зворотне перетворення знаходить шляхом перекидання знака\(v\). Поставивши наш частотний вектор через зворотний імпульс Лоренца, ми знаходимо
\[\omega ' = \gamma \omega (1 + v\cos \theta )\]
Для\(θ = 0\) доплерівського коефіцієнта знижується до
\[γ(1+v) = D\]
який відновлює\(1 + 1\) -мірний результат. Бо\(\theta = 90^{\circ}\), ми маємо\(ω' = γω\), що інтерпретується як ефект розширення чистого часу, коли рух джерела є поперечним до прямої видимості.
Щоб побачити силу математичних інструментів, які ми розробили в цьому розділі, ви можете переглянути розділи 6 та 7 статті Ейнштейна 1905 року про спеціальну відносність, де потрібна тривала деривація, щоб досягти того ж результату.
аберація
Уявіть, що дощ падає вертикально, поки ви їдете в кабріолеті зверху вниз. Для вас краплі дощу, здається, рухаються під деяким ненульовим кутом відносно вертикалі. Це називається аберацією.
Визначення: аберація
Напрямок світової лінії змінюється залежно від своєї системи відліку.
У системі відліку вулиці кут між трьома швидкостями дощу і автомобілем є\(\theta = 90^{\circ}\), але в рамі автомобіля\(\theta ' \neq 90^{\circ}\). У цьому прикладі аберація є великим ефектом, оскільки швидкість автомобіля\(v\) порівнянна зі швидкістю\(u\) крапель дощу. Щоб равлик повзав по тротуару набагато нижче\(v\), ефект був би невеликим. Використовуючи малокутове наближення\(\tan \epsilon \approx \epsilon\), ми виявляємо\(v\), що для малих різниця\(∆θ = θ' - θ\) буде приблизно\(v/u\), в одиницях радіанів.
Порівняно з променем світла, ми всі схожі на равликів. Наприклад, орбітальна швидкість Землі приблизно\(v ∼ 10^{-4}\) в одиницях, де швидкість світла\(u = 1\), тому ми очікуємо максимального ефекту близько\(10^{-4}\) радіанів, або\(2'' \) дуги, яка невелика, але не незначна для телескопа з високоякісним кріпленням, який використовується при великому збільшенні.
Ця оцінка астрономічної аберації світла приблизно правильна, але ми не очікуємо, що вона буде точною, як через малокутове наближення, так і тому, що ми обчислили її, використовуючи галілейську картину простору-часу. Давайте розрахуємо точний результат. Як показано в прикладі 6.6.1, напрямок поширення світлової хвилі лежить уздовж вектора, який є подвійним до її частотного ковектора. Назвемо цей напрямок поширення\(\to u\). Повторне використання виразу для\(ω\to \) визначеного вище, і\(\to u\) довільно фіксуючи timeslike компонент бути\(1\), ми маємо
\[\to u = (1,-\cos\theta ,-\sin\theta )\]
Коли цей вектор зазнає поштовху\(v\) вздовж\(x\) - осі він стає
\[\to u' = \left ( \gamma (1 + v\cos \theta ), \gamma (-v - v\cos \theta ), -\sin \theta \right )\]
Оригінальний кут
\[\theta = \tan^{-1}\frac{u_y}{u_x}\]
було перетворено на
\[\theta ' = \tan^{-1}\frac{u_y'}{u_x'}\]
результат буття
\[\tan \theta ' = \frac{\sin \theta }{\gamma (\cos \theta + v)}\]
Приклад\(\PageIndex{1}\): A test of special relativity
Припущення, що лежить в основі цієї обробки аберації, полягало в тому\(u = c\), що швидкість світла була, незалежно від швидкості джерела. Не всі пререлятивістські теорії мали цю властивість, і можна було б очікувати, що в такій теорії аберація не буде відповідати релятивістському результату. Зокрема, припустимо, що ми вірили в галілеївський простор часу, так що коли далека галактика, відступаючи від нас з деякою швидкістю\(w\), випромінювала промінь світла на нас, швидкість світла в нашому кадрі була\(u = c - w\). Тобто ми уявляємо собі теорію, в якій випромінювання променя світла - це як стріляти кулею з пістолета. Оскільки ефекти аберації йдуть приблизно так\(v/u\), ми очікуємо, що зменшення\(u\) призведе до більшої аберації порівняно з прогнозом відносності.
Щоб перевірити теорії цього типу, Гекманн 1 використовував\(24\) дюймовий відбивач у Гамбурзі, щоб взяти фотографічні пластини з великим збільшенням зоряного поля в Великій Урсі, що містять\(11\) зірки всередині Чумацького Шляху та\(5\) далеких галактик. Вимірювання доплерівських зрушень показали, що галактики відступають від нас зі швидкостями близько\(w = 0.05c\), тоді як зірки в межах Чумацького Шляху рухаються відносно нас зі швидкостями, незначними в порівнянні. Якби, всупереч релятивістському прогнозу\(u\), це призвело до\(5\%\) зниження, то ми очікували б про\(5\%\) збільшення аберації для галактик порівняно з зірками.
Протягом року орбіта Землі переносить її в бік і від Великої Ведмедиці, так що в земній системі відліку зірки і галактики мають різні швидкості відносно нас, а ефект\(∼20''\) аберації коливається в напрямку. Якщо ефект був різним для галактик і зірок, то вони повинні зміщувати свої видимі позиції відносно один одного. Зсув повинен бути в порядку\(2000\), або одна секунда дуги.\(5\%\) Результати спостережень показали, що ці відносні положення, здається, не змінювалися взагалі протягом року, при цьому середній відносний зсув був\(0.00±0.06''\) дугою. Ця різниця в аберації узгоджується з нулем, як передбачається спеціальною відносністю.
Приклад\(\PageIndex{2}\): The view of an ultrarelativistic observer
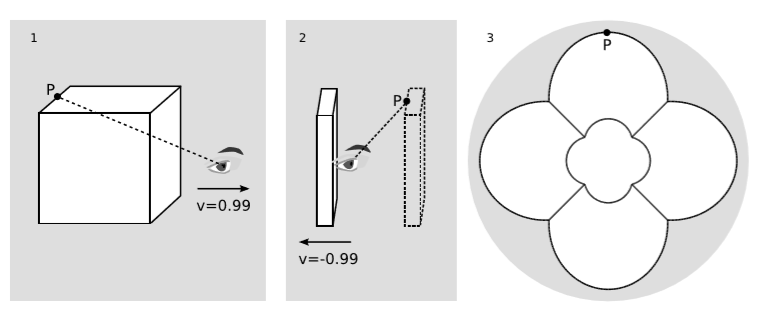
\(\PageIndex{1}\)На малюнку показана візуалізація спостерігача, що летить крізь куб на\(v = 0.99\). На малюнку\(\PageIndex{1}\) (1) куб зображений у власному кадрі відпочинку, де він має сторони одиничної довжини, а спостерігач, вже пройшовши наскрізь, лежить на одну одиницю праворуч від центру куба. Спостерігач звернений вправо, подалі від куба. Пунктирна лінія - це промінь світла, який рухається від точки\(P\) до спостерігача, і в цьому кадрі він виглядає так, ніби промінь, що надходить з\(\theta = 162^{\circ}\), не потрапив би в око спостерігача.
Але в кадрі спостерігача, фігура\(\PageIndex{1}\) (2), промінь знаходиться в\(\theta ' = 47^{\circ}\), так що він насправді потрапляє в її поле зору. Куб по довжині скорочується на коефіцієнт\(γ ≈ 7\). Промінь випромінювався раніше, коли куб виходив перед спостерігачем, в положенні, показаному пунктирним контуром.
Зображення, яке бачить спостерігач, показано на малюнку\(\PageIndex{1}\) (3). Циркулярний контур, що визначає поле зору, представляє\(\theta ' = 50^{\circ}\). Зверніть увагу, що релятивістське скорочення довжини зовсім не те, що бачить спостерігач оптично. На оптичне спостереження впливає скорочення довжини, а також аберація та час, необхідний для поширення світла до спостерігача. Час поширення різний для різних частин куба, тому в кадрі спостерігача, малюнок\(\PageIndex{1}\) (2), промені з різних точок повинні були випромінюватися, коли куб знаходився в різних точках свого руху, якщо ці промені повинні були дістатися до ока.
Група в Австралійському національному університеті створила анімації подібних сцен, які можна знайти в Інтернеті, шукаючи «оптичні ефекти особливої відносності».
На відео показані фотореалістичні зображення зменшених сцен. Це означає, що швидкість світла була сповільнена з більш ніж одного мільярда кілометрів на годину до швидкості лише одного метра в секунду. Наслідки цієї вигадки були обмежені оптичними ефектами і дозволяє нам бачити спеціальні релятивістські ефекти, неможливі в повсякденному житті.
Приємно уявити собі погляд спостерігача на борту ультрарелятивістського зорелятивістського корабля. Для\(v\) досить близьких до\(1\), будь-який кут\(\theta < 180^{\circ}\) перетворюється на невеликий\(θ'\). Таким чином, все світло, що надходить до цього спостерігача від навколишніх зірок — навіть тих, що знаходяться в крайніх зворотних напрямках! — зібраний у невелику яскраву пляму світла, яка, здається, виходить прямо вперед. Деяке видиме світло буде зміщено в екстремальне ультрафіолетове та інфрачервоне, тоді як деяке інфрачервоне та ультрафіолетове світло стане видимим.
