9.3: Гравітаційне випромінювання (частина 2)

У цьому розділі ми вивчаємо кілька прикладів точних розв'язків польових рівнянь. Кожен з них можна легко показати, що це не просто координатна хвиля, оскільки в кожному випадку тензор Рімана має ненульові елементи.

Приклад 1. Точне рішення

Ми вже бачили, наприклад, у виведенні метрики Шварцшильда в розділі 6.2, що коли ми отримаємо приблизне рішення рівнянь загальної відносності, ми зможемо знайти послідовне рішення. Історично такий підхід використовувався лише в крайньому випадку, оскільки відсутність комп'ютерів зробило розрахунки занадто складними для обробки, і тенденція полягала в тому, щоб шукати хитрощі, які зробили б можливим рішення закритої форми. Але сьогодні метод серії має ту перевагу, що будь-який простий смертний може мати якусь розумну надію на успіх з ним - і немає нічого більш нудного (або деморалізуючого), ніж трудомістке вивчення чужого спеціального трюку, який працює лише для конкретної проблеми. У цьому прикладі ми побачимо, що такий підхід наближається до забезпечення точного коливального плоского хвильового рішення польових рівнянь.

Нашим найкращим рішенням до цих пір була форма

\[ds^{2} = dt^{2} - (1 + f) dx^{2} - \frac{dy^{2}}{1 + f} - dz^{2}, \tag{9.2.6}\]

де f = Асін (z − t). Це не здається точним рішенням для великих амплітуд, оскільки координати x та y обробляються асиметрично. В крайньому випадку |A| ≥ 1, в g _yy були б особливості, але не в g _xx. Зрозуміло, що метрика повинна мати якусь нелінійну залежність від f, але ми просто не знайшли цілком правильну нелінійну залежність. Припустимо, ми спробуємо щось такого виду:

\[ds^{2} = dt^{2} - (1 + f + cf^{2}) dx^{2} - (1 - f + df^{2}) dy^{2} - dz^{2} \tag{9.2.7}\]

Це приблизно зберігає обсяг, оскільки (1+f +.) (1−f +.) дорівнює одиниці, аж до порядку f ². Наступна програма тестує цю форму.

У рядку 3 мотивація використання складної експоненціальної, а не синусоїди в f є звичайною для отримання більш простих виразів; як ми побачимо, це в кінцевому підсумку викликає проблеми. У рядках 5 і 6 символи c і d не були визначені і не оголошені як залежні від інших змінних, тому Maxima розглядає їх як невідомі константи. Результатом є G _tt (4d + 4c − 3) A ² для малих A, тож ми можемо змусити термін A ² зникнути відповідним вибором d та c Для симетрії вибираємо c = d =\(\frac{3}{8}\). При цих значеннях констант результат для G _tt порядку A ⁴. Ця методика може бути розширена на вищі та вищі порядки наближення, що призводить до точного розв'язання рядів польових рівнянь.

На жаль, вся історія закінчується занадто гарною, щоб бути правдою. Отримана метрика має складнозначні елементи. Якби загальна теорія відносності була лінійною теорією поля, то можна було б застосувати звичайну техніку формування лінійних комбінацій виразів виду е ^+i... і e ^−i... , Щоб дати реальний результат. Але польові рівняння загальної відносності нелінійні, тому отримана лінійна комбінація вже не є рішенням. Найкраще, що ми можемо зробити, це зробити неколивальне реальне експоненціальне рішення (задача 2).

Приклад 2: Точне коливальне, немонохроматичне рішення

Припустимо метрику форми

\[ds^{2} = dt^{2} - p(z - t)^{2} dx^{2} - q(z - t)^{2} dy^{2} - dz^{2}, \ldots \tag{9.2.8}\]

де p і q - довільні функції. Така метрика чітко представляла б якусь поперечно-поляризовану плоску хвилю, що рухається зі швидкістю c (= 1) у напрямку z. Наступний код Maxima обчислює його тензор Ейнштейна.

Результат пропорційний\(\frac{\ddot{q}}{q} + \frac{\ddot{p}}{p}\), тому будь-які функції p і q, які задовольняють диференціальному\(\frac{\ddot{q}}{q} + \frac{\ddot{p}}{p}\) рівнянню = 0, призведуть до вирішення польових рівнянь. Встановлюючи p (u) = 1 + Acos u, наприклад, знаходимо, що q коливальний, але з періодом довше 2\(\pi\) (задача 3).

Приклад 3: Точна, плоска, монохроматична хвиля

Будь-яка метрика форми

\[ds^{2} = (1 - h) dt^{2} - dx^{2} - dy^{2} - (1 + h) dz^{2} + 2hdzdt, \tag{9.2.9}\]

де h = f (z − t) xy, а f - будь-яка функція, є точним розв'язком польових рівнянь (задача 4).

Оскільки h пропорційний xy, це не здається на перший погляд рівномірною плоскою хвилею. Однак можна перевірити, що всі складові тензора Рімана залежать лише від z − t, а не від x або y, тому немає вимірної властивості цієї метрики, яка змінюється з x та y.

Швидкість випромінювання

Як ми можемо знайти швидкість гравітаційного випромінювання від такої системи, як пульсар Халса-Тейлора?

Давайте продовжимо за аналогією. Найпростішим джерелом звукових хвиль є щось на зразок конуса стереодинаміка. Оскільки типові звукові хвилі мають довжини хвиль, вимірювані в метрах, весь динамік, як правило, невеликий порівняно з довжиною хвилі. Конус динаміка являє собою поверхню коливального зміщення\(x = x__o \sin \omega t\). Ідеалізуючи таке джерело до радіально пульсуючої сферичної поверхні, ми маємо коливальний монополь, який випромінює звукові хвилі рівномірно у всіх напрямках. Щоб знайти випромінювану потужність, відзначимо, що швидкість джерела-поверхні пропорційна х _о\(\omega\), тому кінетична енергія повітря, що безпосередньо контактує з нею, пропорційна\(\omega^{2}x^2_o\). Отже, випромінювана потужність пропорційна\(\omega^{2} x^2_o\).

Малюнок\(\PageIndex{7}\): Потужність, що випромінюється багатополюсним джерелом порядку\(m\)\(\omega^{2(m+1)}\), пропорційна, коли розмір джерела невеликий в порівнянні з довжиною хвилі. Основна причина ω залежності полягає в тому, що на низьких частотах довжина хвилі довга, тому кількість довжин хвиль, пройдених до певної точки в просторі, майже однакова з будь-якої точки джерела; тому ми отримуємо сильне скасування.

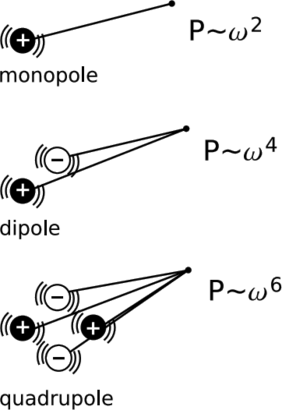
При електромагнетизмі збереження заряду забороняє існування коливається електричного монополя. Таким чином, найпростішим джерелом випромінювання є коливальний електричний диполь D = D _o sin\(\omega\) t Якщо фізичний розмір диполя невеликий порівняно з довжиною хвилі випромінювання, то випромінювання є неефективним процесом; в будь-якій точці простору існує лише невелика різниця в довжині шляху між позитивними та негативними частинами диполя, тому, як правило, спостерігається сильне скасування їхніх внесків, які випромінювалися з протилежними фазами. Результатом є те, що електромагнітний потенціал хвилі чотиривекторний (Розділ 4.2) пропорційний D _o\(\omega\), поля D _o\(\omega^{2}\), а випромінювана потужність - D ² _o\(\omega^{4}\). Коефіцієнт\(\omega^{4}\) може бути розбитий на (\(\omega^{2}\)\(\omega^{2}\)) (), де перший фактор\(\omega^{2}\) виникає з причин, подібних до тих, що пояснюють\(\omega^{2}\) фактор монопольного випромінювання звуку, тоді як другий\(\omega^{2}\) виникає, тому що чим менше ω, тим довше довжина хвилі, і тим більша неефективність випромінювання, викликана малим розміром джерела порівняно з довжиною хвилі.

Приклад 4: радіо

Комерційне AM радіо використовує довжини хвиль кілька сотень метрів, тому AM дипольні антени зазвичай на порядки коротше довжини хвилі. Це викликає сильне ослаблення як при передачі, так і при прийомі. (Існують теореми, звані теоремами взаємності, які пов'язують ефективність передачі з ефективністю прийому.) Тому приймачі повинні використовувати велику кількість посилення. Це не викликає проблем, оскільки навколишні джерела радіочастотного шуму послаблюються короткою антеною так само сильно, як і сигнал.

Оскільки наш Всесвіт, здається, не має частинок з негативною масою, ми не можемо сформувати гравітаційний диполь, поклавши позитивні та негативні маси на протилежні кінці палиці - і, крім того, така паличка не буде вільно обертатися навколо свого центру, оскільки її центр маси не лежить в її центрі! У більш реалістичній системі, наприклад пульсарі Халсе-Тейлора, ми маємо дві нерівні маси, що обертаються навколо їх загального центру маси. Зберігаючи імпульс, масовий дипольний момент такої системи є постійним, тому ми не можемо мати коливальний диполь маси. Найпростішим джерелом гравітаційного випромінювання, таким чином, є квадруполь коливальної маси, Q = Q _o sin\(\omega\) t Як і у випадку коливального електричного диполя, випромінювання пригнічується, якщо, як це зазвичай буває, джерело невелике порівняно з довжиною хвилі. Придушення ще сильніше в разі квадруполя, і в результаті виходить, що випромінюється потужність пропорційна Q ² _o\(\omega^{6}\).

Цей результат має цікаву властивість бути інваріантним при масштабуванні координат. У геометризованих одиницях маса, відстань та час мають однакові одиниці, так що Q ² _o має одиниці (довжина ³) ², а\(\omega^{6}\) одиниці (довжина) ⁻⁶. Це саме те, що потрібно, тому що в геометризованих одиницях потужність безрозмірна, енергія/час = довжина/довжина = 1.

Ми також можемо прив'язати\(\omega^{6}\) залежність до нашого попереднього аргументу щодо розсіювання енергії гравітаційними хвилями. Аргумент полягав у тому, що гравітаційні тіла піддаються затриманим за часом гравітаційним силам, внаслідок чого орбіти мають тенденцію до розпаду. Цей аргумент працює лише в тому випадку, якщо сили змінюються в часі; якщо сили постійні з часом, то затримка часу не впливає. Наприклад, в напівньютонівському межі поле листа маси не залежить від відстані від листа. (Електричний аналог цього факту легко довести за допомогою закону Гаусса.) Якщо два паралельних листа падають один до одного, то жоден не піддається змінній в часі сили, тому випромінювання не буде. Загалом, ми очікуємо, що гравітаційного випромінювання від частинки не буде, якщо третя похідна її положення d3 x/dt 3 не буде ненульовою. (Те ж саме стосується електричного квадрупольного випромінювання.) В особливому випадку, коли положення коливається синусоїдально, правило ланцюга говорить нам, що прийняття третьої похідної еквівалентно виведенню коефіцієнта\(\omega^{3}\). Оскільки амплітуда гравітаційних хвиль пропорційна\(\frac{d^{3} x}{dt^{3}}\), їх енергія змінюється як (\(\frac{d^{3} x}{dt^{3}}\)) ², або\(\omega^{6}\).

Загальна картина, яку ми спостерігали, полягає в тому, що для багатопольного випромінювання порядку m (0=монополь, 1 = диполь, 2=квадруполь), випромінюється потужність залежить від\(\omega^{2(m+1)}\). Оскільки гравітаційне випромінювання завжди повинно мати m = 2 або вище, у нас дуже крута\(\omega^{6}\) залежність потужності від частоти. Це свідчить про те, що якщо ми хочемо побачити сильне гравітаційне випромінювання, нам потрібно подивитися на системи, які коливаються надзвичайно швидко. Для двійкової системи з нерівними масами порядку m, з орбітами, що мають радіуси порядку r, маємо Q _o mr ². Закони Ньютона\(\omega\) дають m ^1/2 r ^−3/2, що по суті є законом періодів Кеплера. В результаті виходить, що випромінюється потужність повинна залежати від (\(\frac{m}{r}\)) ⁵. Повторно вставляючи правильні константи, щоб дати рівняння, яке дозволяє практичний розрахунок в одиницях СІ, ми маємо

\[P = k \frac{G^{4}}{c^{5}} \left(\dfrac{m}{r}\right)^{5}, \tag{9.2.10}\]

де k - безодинична константа одиниці порядку.

Для пульсара Хулса-Тейлора ¹² ми маємо m 3 × 10 ³⁰ кг (близько півтори сонячної маси) і r 10 ⁹ м Бінарний пульсар виготовлений на замовлення наших цілей, оскільки надзвичайно великий порівняно з\(\frac{m}{r}\) тим, що бачить майже в будь-якій іншій астрономічній системі. Отримана оцінка по потужності становить близько 10 ²⁴ Вт. Період пульсара спостерігається стабільно подовжується зі швидкістю\(\alpha\) = 2.418 × 10 ⁻¹² секунд в секунду. Щоб порівняти це з нашою сирої теоретичною оцінкою, візьмемо ньютонівську енергію системи\(\frac{Gm^{2}}{r}\) і множимо на\(\omega \alpha\), даючи 10 ²⁵ Вт, що перевіряється з точністю до порядку. Повний загально-релятивістський розрахунок відтворює\(\alpha\) спостережуване значення to в межах 0,1% смуг похибки даних.

Посилання

¹² http://arxiv.org/abs/astro-ph/0407149