9.2: Гравітаційне випромінювання (частина 1)

емпіричні докази

Перші сильні емпіричні свідчення гравітаційних хвиль з'явилися в 1982 році. Система Халсе-Тейлора (розділ 6.2) містить дві нейтронні зірки, що обертаються навколо їх загального центру мас, і період орбіти спостерігається поступово зменшується з плином часу (рис. 9.2.1). Це трактується як доказ того, що зірки втрачають енергію на випромінювання гравітаційних хвиль. ⁴ Як ми побачимо пізніше, швидкість втрати енергії відмінно узгоджується з прогнозами загальної відносності.

Малюнок\(\PageIndex{1}\) - Орбітальний рух пульсара Халсе-Тейлора поступово втрачає енергію через випромінювання гравітаційних хвиль. Лінійне зменшення періоду інтегровано на цій ділянці, в результаті чого виникає парабола. Від Вайсберга та Тейлора, http://arxiv.org/abs/astro-ph/0211217.

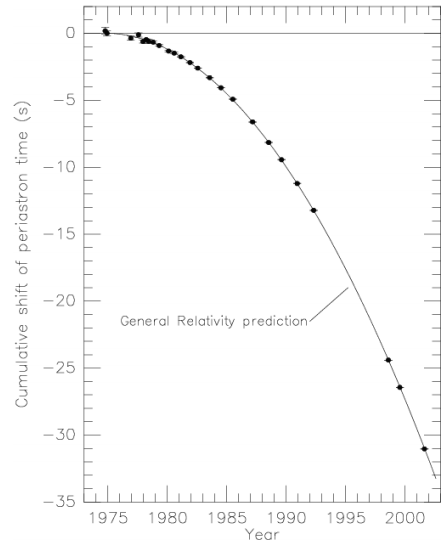
Ще більш драматичним, якщо менш чітким, доказом є спостереження Комоси, Чжоу та Лу ⁵ надмасивної чорної діри, яка, здається, відкидається від батьківської галактики зі швидкістю 2650 км/с (проектується вздовж прямої видимості). Вони трактують це як доказ для наступного сценарію. У ранньому Всесвіті галактики утворюються з надмасивними чорними дірами в їх центрах. При зіткненні двох таких галактик чорні діри можуть зливатися. Злиття - це жорстокий процес, в якому випромінюються інтенсивні гравітаційні хвилі, і ці хвилі несуть велику кількість імпульсу, змушуючи чорні діри віддалятися зі швидкістю, більшою за швидкість втечі об'єднаної галактики.

Хоча втрати енергії від таких систем, як двійковий Hulse-Taylor, дають вагомі докази того, що гравітаційні хвилі існують і несуть енергію, фізики та астрономи все ще хотіли виявити їх безпосередньо, і серйозні спроби проектування та побудови таких систем почалися приблизно в 1962 році. Конструкція, яка нарешті досягла успіху, використовували інтерферометри, які виявляють коливання в довжині власних рук. Перша гравітаційно-хвильова подія була виявлена цим методом у 2016 році співпрацею Advanced LIGO. ⁶ Вважається, що подія стала результатом зіткнення двох чорних дір.

Малюнок\(\PageIndex{2}\) - Гравітаційна форма хвилі, що спостерігається в 2016 році Advanced Ligo.

У 2017 році подія, інтерпретована як зіткнення двох нейтронних зірок, була виявлена як гравітаційним, так і електромагнітним випромінюванням, перевіряючи з високою точністю, що гравітаційні хвилі поширюються при c.

Хоча раніше 2016 зіткнення чорних дір безпосередньо не порівнювало поширення світла та гравітації, це забезпечило інший вид перевірки поширення гравітаційних хвиль при c Форма хвилі, виявлена в цьому випадку, була «щебетання», яка ковзала вгору по частоті, коли чорні діри спіралі наближалися до один одного і прискорилися. Оскільки хвиля перебувала в дорозі більше мільярда років, а форма хвилі тривала частку секунди, випливає, що гравітаційні хвилі в цьому діапазоні частот рухаються з дуже майже однаковою швидкістю, тобто існує дуже жорстка верхня межа розсіювання гравітаційних хвиль.

Додаткова космічна система, LISA, була запропонована до запуску в 2020 році, але її фінансування є невизначеним. Два пристрої працювали б в додаткових діапазонах частот (рис. 9.2.3). Точка продажу LISA полягає в тому, що якщо він запускається, на небі є ряд джерел, з відомими властивостями, які, як відомо, легко знаходяться в межах його чутливості. ⁷ Одним відмінним кандидатом є HM Cancri, пара білих карликів з орбітальним періодом 5,4 хвилини, коротше, ніж у будь-якої іншої відомої бінарної зірки. ⁸

Малюнок\(\PageIndex{3}\) - Прогнозовані чутливості LISA і LIGO до гравітаційних хвиль різних частот.

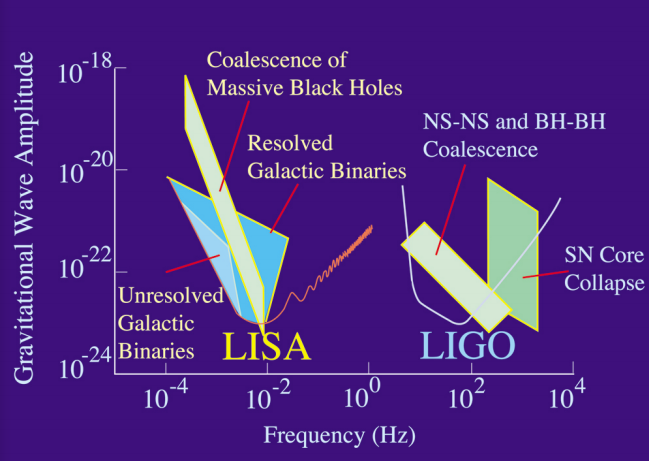
Енергетичний вміст

Навіть не виконуючи розрахунків для такої системи, як двійковий файл Халсе-Тейлора, легко показати, що якщо такі хвилі існують, вони повинні бути здатні нести енергію. Розглянемо дві рівні маси на високо еліптичних орбітах навколо їх загального центру мас, рис. 9.2.4. Рух майже одновимірний. Оскільки маси відступають одна від одної, вони відчувають затримку версії гравітаційної сили, що походить від часу, коли вони були ближче один до одного, і сила була сильнішою. Результатом є те, що в ближньому ньютонівському межі вони втрачають більше кінетичної та гравітаційної енергії, ніж втратили б у чисто ньютонівській теорії. Тепер вони повертаються всередину по своїх орбітах. Коли вони наближаються один до одного, затримка за часом сила аномально слабка, тому вони отримують менше механічної енергії, ніж очікувалося. Результатом є те, що з кожним циклом втрачається механічна енергія. Ми очікуємо, що ця енергія переноситься хвилями так само, як радіохвилі несуть енергію, втрачену передавальною антеною. ⁹

Малюнок\(\PageIndex{4}\) - Коли дві планети відступають одна від одної, кожна відчуває гравітаційне тяжіння, яке інша чинила у своєму попередньому положенні, затримується на той час, коли гравітаційні ефекти поширюються на c. до ближчого положення лівої планети в більш ранній час t', а не її поточне положення на t Механічна енергія не зберігається, і орбіти розпадуться

Примітка

Потрібно бути обережним з цим типом аргументів. Зокрема, можна отримати неправильні правильні результати, намагаючись узагальнити цей одновимірний аргумент до руху в більш ніж одному вимірі, оскільки ефективна напівньютонівська взаємодія - це не просто відкладена за часом версія закону Ньютона; вона також включає в себе сили, залежні від швидкості. Нескладно зрозуміти, чому така швидкість-залежність повинна виникати в більш простому випадку електромагнетизму. Припустимо, що заряди А і В не знаходяться в спокої відносно один одного. У кадрі B електричне поле від А повинно виходити з напрямку положення, яке спостерігач, що рухається з B, екстраполює лінійно з останнього відомого положення та швидкості А, як визначено розрахунком швидкості світла. Це випливає з інваріантності Лоренца, оскільки це напрямок, який побачить спостерігач, що рухається з А. повне обговорення дається Carlip, arxiv.org/abs/gr-qc/9909087v2.

Ці хвилі не тільки можуть видалити механічну енергію з системи, вони також можуть депонувати енергію в детекторі, як показано нематематичним «липким аргументом з бісеру» (рис. 9.2.5), який був виник Фейнманом у 1957 році і пізніше популяризований Бонді.

Малюнок\(\PageIndex{5}\) - Т він липкий кулька аргумент за реальність гравітаційних хвиль. Коли гравітаційна хвиля з відповідною поляризацією проходить повз, кулька вібрує вперед і назад на стрижні. Тертя створює тепло. Це демонструє, що гравітаційні хвилі несуть енергію, і, таким чином, є реальними, що спостерігаються явищами.

Тепер, строго кажучи, ми лише показали, що гравітаційні хвилі можуть витягувати або дарувати механічну енергію, але не те, що самі хвилі передають цю енергію. Різниця не є тією, яка зазвичай зустрічається з нами, оскільки ми навчені вірити, що енергія завжди зберігається. Але ми знаємо, що з фундаментальних причин загальна відносність не має глобальних законів збереження, які застосовуються до всіх просторових часів (розділ 4.5). Можливо, енергія, втрачена системою Халсе-Тейлора, просто зникла, ніколи не з'являтися знову, а енергія, що передається липкій кульці, просто генерується з нізвідки. З іншого боку, загальна відносність має глобальні закони збереження для певних конкретних класів просторових часів, включаючи, наприклад, збережену скалярну масову енергію у випадку стаціонарного просторового часу (розділ 7.1). Простір, що містить гравітаційні хвилі, не є нерухомими, але, можливо, є щось подібне, що ми можемо зробити в якомусь відповідному особливому випадку.

Припустимо, ми хочемо вираз для енергії гравітаційної хвилі з точки зору її амплітуди. Це здається, що це повинно бути простим. Такі вирази ми маємо в інших класичних польових теоріях. При електромагнетизмі ми маємо енергетичні щільності + (\(\frac{1}{8 \pi k}\)) | E | ² і + (\(\frac{1}{2 \mu_{o}}\)) | B | ² пов'язані з електричним і магнітним полями. У ньютонівській гравітації ми можемо призначити щільність енергії − (\(\frac{1}{8 \pi G}\)) | g | ² гравітаційному полю g; знак мінус вказує на те, що коли маси сягають один на одного, вони виробляють більше поле, і енергія вивільняється.

Однак загалом відносність принцип еквівалентності говорить нам, що для будь-якого гравітаційного поля, виміряного одним спостерігачем, ми можемо знайти іншого спостерігача, того, хто вільно падає, який каже, що локальне поле дорівнює нулю. Звідси випливає, що ми не можемо точно пов'язувати енергію з кривизною певної області простору-часу. Найкраще, що ми можемо зробити, це знайти вирази, які дають щільність енергії (1) в межі слабких полів, і (2) при усередненні по області простору, яка велика порівняно з довжиною хвилі. Ці вирази не є унікальними. Існує ряд способів їх написання в терміні метрики і її похідних, і всі вони дають однаковий результат у відповідному ліміті. Читач, який зацікавлений детально побачити тему, розроблену, посилається на конспекти Керролла про загальну відносність, arxiv.org/abs/gr-qc/? 9712019. Хоча така річ технічно брудна, ми можемо досягти зовсім небагато, просто знаючи, що такі результати існують, і що, хоча вони не є унікальними в цілому, вони однозначно добре визначені в певних випадках. Зокрема, коли хочеться обговорити гравітаційні хвилі, зазвичай можна припустити асимптотично плоский простор-час. У асимптотично плоскому просторовічасу існує скалярна масова енергія, яка називається масою ADM, яка зберігається. У цьому обмеженому сенсі ми впевнені, що книги балансують, і що випромінювання та поглинання гравітаційних хвиль дійсно означає передачу фіксованої кількості енергії.

Очікувані властивості

Щоб побачити, які властивості слід очікувати від гравітаційного випромінювання, спочатку розглянемо міркування, які призвели до побудови тензорів Річчі та Ейнштейна. Якщо певний обсяг простору заповнений тестовими частинками, то тензори Річчі і Ейнштейна вимірюють тенденцію до цього обсягу до «прискорення»; тобто\(− \frac{d^{2} V}{dt^{2}}\) є мірою тяжіння будь-якої маси, що лежить всередині об'єму. Віддалена маса, однак, буде чинити лише приливні сили, які спотворюють область, не змінюючи її обсягу. Це говорить про те, що в міру проходження гравітаційної хвилі через певну область простору вона повинна спотворювати форму даної області, не змінюючи її обсягу.

Коли вперше обговорювалася ідея гравітаційних хвиль, був певний скептицизм щодо того, чи представляють вони ефект, який можна спостерігати, навіть в принципі. Найбільш наївний такий сумнів має той самий аромат, що і той, який обговорюється в розділі 8.2 про спостережливість розширення Всесвіту: якщо все спотворюється, то чи не спотворюються наші метрові палички, що унеможливлює вимір ефекту? Відповідь така ж, як і раніше в розділі 8.2; системи, які гравітаційно або електромагнітно пов'язані, не мають своїх шкал спотворених на величину, рівну зміні елементів метрики.

Малюнок\(\PageIndex{6}\) - У міру поширення гравітаційної хвилі в напрямку z метрика коливається в х і y напрямках, зберігаючи об'єм.

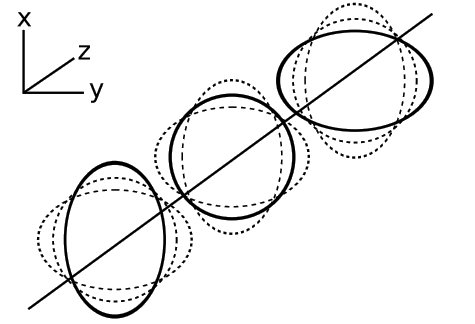
Менш наївною причиною скептично ставитися до гравітаційних хвиль є те, що лише тому, що метрика виглядає коливальною, це не означає, що його коливальна поведінка спостерігається. Розглянемо наступний приклад.

\[ds^{2} = dt^{2} - \left(1 + \dfrac{1}{10} \sin x \right) dx^{2} - dy^{2} - dz^{2}\]

Символи Крістоффеля залежать від похідних форми\(\partial_{a} g_{bc}\), тому тут єдиний незникаючий символ Крістоффеля є\(\Gamma^{x}_{xx}\). Тоді просто перевірити, що тензор Рімана

\[R^{a}_{bcd} = \partial_{c} \Gamma^{a}_{db} − \partial_{d} \Gamma^{a}_{cb} + \Gamma^{a}_{ce} \Gamma^{e}_{db} − \Gamma^{a}_{de} \Gamma^{e}_{cb}\]

зникає симетрією. Тому ця метрика дійсно повинна бути метрикою з плоским простором часу, яка була піддана дурній зміні координат.

Вправа\(\PageIndex{1}\)

Самоперевірка: R\(\Gamma\) зникає, але ні. Чи є причина приділяти більше уваги тому чи іншому?

Щоб кривизна не зникла, схоже, нам потрібна метрика, в якій коливання не обмежується однією змінною.

Наприклад, метрика

\[ds^{2} = dt^{2} - \left(1 + \frac{1}{10} \sin y \right) dx^{2} - dy^{2} - dz^{2}\]

має незникаючу кривизну. Іншими словами, здається, що ми повинні шукати поперечні хвилі, а не поздовжні. ¹⁰ З іншого боку, ця метрика не може бути розв'язком рівнянь вакуумного поля, оскільки вона не зберігає об'єм. Він також стоїть на місці, тоді як ми очікуємо, що рішення польових рівнянь повинні поширюватися зі швидкістю світла, принаймні для малих амплітуд. Ці висновки є самоузгодженими, оскільки поляризація хвилі може бути обмежена лише в тому випадку, якщо вона поширюється при c (див. Розділ 4.2).

Примітка

0A більш ретельне ставлення показує, що поздовжні хвилі завжди можна інтерпретувати як фізично неспостережувані координатні хвилі, в межі великих відстаней від джерела. З іншого боку, зрозуміло, що жодна така заборона проти поздовжніх хвиль не може застосовуватися повсюдно, оскільки таке обмеження може бути інваріантним лише в тому випадку, якщо хвиля поширюється при c (див. Розділ 4.2), тоді як високоамплітудні хвилі не повинні поширюватися на c. поздовжні хвилі біля джерела називаються розчинами типу III в класифікаційній схемі завдяки Петрову. Поперечні хвилі, які ми могли б насправді спостерігати в практичних експериментах, - це тип N.

Виходячи з того, що ми з'ясували, наступне здається метрикою, яка може мати бойовий шанс представити реальну гравітаційну хвилю:

\[ds^{2} = dt^{1} - (1 + A \sin (z - t)) dx^{2} - \frac{dy^{2}}{1 + A \sin (z - t)} - dz^{2}\]

Він поперечний, він поширюється при c (= 1), а той факт, що g _xx - зворотний g _yy робить його об'ємно-зберігаючим. Наступна програма Maxima обчислює свій тензор Ейнштейна:

Для представницької складової тензора Ейнштейна знаходимо

\[G_{tt} = \frac{A^{2} \cos^{2} (z - t)}{2 + 4 A \sin (z - t) + 2A^{2} \sin^{2} (z - t)}\]

Для малих значень A ми маємо |G _tt |\(\lesssim \frac{A^{2}}{2}\). Рівняння вакуумного поля вимагають G _tt = 0, тому це не точне рішення. Але всі складові G, а не тільки G _tt, мають порядок А ², тому це приблизне рішення рівнянь.

Також просто перевірити, що поширення приблизно в c було необхідною особливістю. Наприклад, якщо замінити множники sin (z −t) у метриці на sin (z −2t), ми отримаємо G _xx, що має одиницю порядку, а не порядку A ².

Щоб довести, що гравітаційні хвилі є спостережуваним ефектом, ми хотіли б мати можливість відобразити метрику, яка (1) є точним рішенням рівнянь вакуумного поля; (2) не просто координатна хвиля; і (3) несе імпульс і енергію. Ще в 1936 році Ейнштейн і Розен опублікували статтю, яка стверджує, що гравітаційні хвилі є математичним артефактом, і насправді не існували. ¹¹

Посилання

⁴ Сходи, «Тестування загальної теорії відносності за допомогою пульсарного хронометражу» relativity.livingreviews.org/... es/lrr-2003-5/

⁵ http://arxiv.org/abs/0804.4585

⁶ https://dcc.ligo.org/LIGO-P150914/public

⁷ Г.Нелеманс, «Передній план галактичної гравітаційної хвилі», arxiv.org/abs/0901.1778v1

⁸ Roelofs et al., «Спектроскопічні докази 5,4-хвилинного орбітального періоду в HM Cancri», arxiv.org/abs/1003.0658v1

¹¹ Частина історії пов'язана на http://en.Wikipedia.org/wiki/Sticky_bead_argument.