7.3: Діаграми Пенроуза та причинно-наслідковий зв'язок

Last updated
Save as PDF

Page ID: 77697

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Ми не можемо безпосередньо візуалізувати чотиривимірний колектор. Однак, коли просторовий час має симетрію, ми можемо візуалізувати відповідні властивості все це, розглядаючи нижчу його частину. За аналогією, якби ми хотіли візуалізувати структуру земних надр, ми могли б намалювати діаграму, яка показує двовимірний перетин через його центр. Насправді, ми могли б позбутися двох вимірів і просто намалювати діаграму однієї радіальної лінії, що проходить від земного ядра до його поверхні; кожна точка на цій лінії тоді представляла б сферу. Якщо ми зробимо це в загальній теорії відносності, для просторучасу, який є сферично симетричним, то ми можемо зменшити чотиривимірне до двовимірного, причому кожна точка представляє двосферу. Застосовуючи деякі подальші хитрощі, ми побачимо, що ми можемо отримати дуже зручну та корисну візуалізацію під назвою діаграма Пенроуза, також відому як діаграма Пенроуза - Картера або причинно-наслідкова діаграма.

Плоский простор-час

Як розминка, на малюнку 7.3.1 показана діаграма Пенроуза для плоского (Мінковського) простору-часу. Діаграма виглядає 1 + 1-мірною, але умовність полягає в тому, що передбачається сферична симетрія, тому ще два виміри приховані, і ми дійсно зображуємо розміри 3 + 1. Типова точка на внутрішній частині алмазної області являє собою 2-сферу. На цьому типі діаграми світлові конуси виглядають так само, як на звичайній просторово-часовій діаграмі простору Мінковського, але шкали відстані сильно спотворюються. Алмаз представляє весь просторовий час, з спотворенням, що вписується всю цю нескінченну область в цю скінченну область на сторінці. Незважаючи на спотворення, на схемі зображені світлоподібні поверхні у вигляді 45-градусних діагоналей. Просторові та часові геодезики, однак, спотворюються, як показано кривими на схемі.

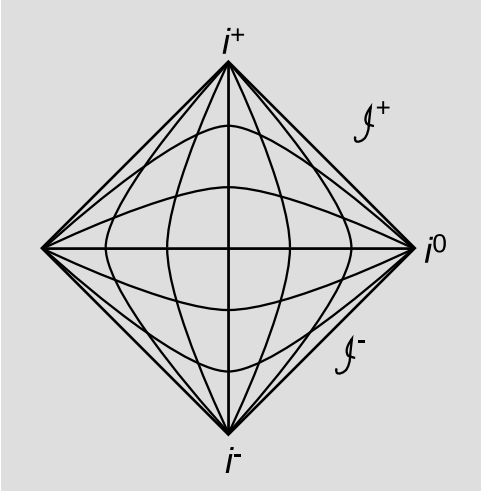
Малюнок 7.3.1.png — Малюнок\(\PageIndex{1}\) - діаграма Пенроуза для плоского просторучасу.

Спотворення стає більшим, коли ми віддаляємося від центру діаграми, і стає нескінченним біля країв. Через це нескінченне спотворення точки i ⁻ та i ⁺ насправді представляють 3-сфери. Усі часові криві починаються з i ⁻ і закінчуються на i ⁺, які є ідеалізованими точками на нескінченності, подібно до точок зникнення на перспективних малюнках. Ми можемо думати про i ⁺ як «кладовищі слонів», де масові частинки йдуть, коли вони вмирають. Аналогічно, світлоподібні криві закінчуються на\(\mathscr{I}^{+}\) (що включає його дзеркальне відображення зліва), іменовані нульовою нескінченністю. ³ Точка в i ⁰ є нескінченно віддаленою кінцевою точкою для просторових кривих. Через сферичної симетрії ліва і права половини діаграми надлишкові.

Можна скласти явні формули, які переводять туди-сюди між координатами Мінковського і точками на діаманті, але в цілому це не обов'язково. Насправді корисність діаграм полягає в тому, що вони дозволяють нам думати про причинно-наслідкові зв'язки координатно-незалежними способами. Світловий конус на схемі виглядає в точності як звичайний світловий конус.

Оскільки цей конкретний простор є однорідним, не має ніякої різниці, яке просторове розташування на діаграмі ми вибираємо як нашу вісь симетрії. Наприклад, ми могли б довільно вибрати лівий кут, центральний часоподібний геодезичний (намальований прямо) або один з інших часоподібних геодезичних (представлений так, ніби він вигнутий).

Шварцшильд Простір Час

Рисунок 7.3.2 - це діаграма Пенроуза для простору Шварцшильда, тобто простору-часу, який виглядає як простір Мінковського, за винятком того, що в ньому є одна вічна чорна діра. Це чорна діра, яка не утворилася гравітаційним колапсом. Цей простор не є однорідним; він має певне місце, яке є центром сферичної симетрії, і це вертикальна лінія зліва, позначена r = 0. Трикутник - це простір всередині горизонту подій; ми могли б скопіювати його через рядок r = 0, якби ми цього хотіли, але копії були б зайвими.

Малюнок 7.3.2.png — Малюнок\(\PageIndex{2}\) - *Діаграма Пенроуза для простору Шварцшильда: чорна діра, яка не утворилася гравітаційним колапсом.*

Діаграма Пенроуза дозволяє легко міркувати про причинно-наслідкові зв'язки. Наприклад, ми бачимо, що якщо частка досягає точки всередині горизонту подій, все її причинне майбутнє лежить всередині горизонту, і всі її можливі майбутні світові лінії перетинають сингулярність. Горизонт є світлоподібною поверхнею, що має сенс, тому що він визначається як межа множини точок, з яких може досягати світловий промінь\(\mathscr{I}^{+}\).

Астрофізична Чорна діра

Малюнок 7.3.3 являє собою діаграму Пенроуза для чорної діри, яка утворилася гравітаційним колапсом. Використовуючи цей тип діаграми, ми можемо стисло розглянути один з найбільш неприємних поширених запитань про чорні діри. (Cf. Розділ 6.3, де ми взяли більш громіздкий підхід без діаграм Пенроуза.) Якщо далекий спостерігач спостерігає за руйнується хмарою матерії, з якого утворюється чорна діра, її оптичні спостереження покажуть, що світло від матерії стає все більш гравітаційно червонозміщеним, і при бажанні вона може інтерпретувати це як приклад гравітаційного розширення часу. Оскільки вона чекає все довше і довше, світлові сигнали від розпалювальної речовини займають більше часу і довше, щоб надходити. Червоний зсув наближається до нескінченності, коли речовина наближається до горизонту, тому світлові хвилі в кінцевому підсумку стають занадто низькими в енергії, щоб їх можна було виявити будь-яким даним інструментом. Крім того, її терпіння (або її життя) закінчиться, тому що час на її годиннику наближається до нескінченності, коли вона чекає, щоб отримати сигнали від матерії, яка наближається до горизонту. Це все точно так, як і повинно бути, так як горизонт за визначенням є межею її спостережуваного Всесвіту. (Світловий промінь, що випромінюється з горизонту, закінчиться на i ⁺, що є кінцевою точкою часових світових ліній, досягнутих лише спостерігачами, які пережили нескінченну кількість належного часу.)

Малюнок 7.3.3.png — Малюнок\(\PageIndex{3}\) - діаграма Пенроуза для чорної діри, утвореної гравітаційним колапсом.

Люди, яких турбують ці питання, часто визнають зовнішню непомітність матерії, що проходить через горизонт, а потім хочуть перейти від цього до таких питань, як: «Чи означає це, що чорна діра ніколи насправді не утворюється?» Це передбачає, що наш далекий спостерігач має однозначно визначене поняття одночасності, яке застосовується до області простору, що тягнеться від її власного положення до внутрішньої частини чорної діри, щоб вона могла сказати, що відбувається всередині чорної діри «зараз». Але поняття одночасності в загальній теорії відносності ще більш обмежене, ніж його аналог в спеціальній теорії відносності. Не тільки одночасність у загальній відносності спостережувач-залежить, як у спеціальній відносності, але вона також є локальною, а не глобальною.

На малюнку 7.3.4 Е - подія на світовій лінії спостерігача. Космічна поверхня S ₁ є одним з можливих «зараз» для цього спостерігача. Відповідно до цієї поверхні, жодна частинка ніколи не потрапляла і не досягала горизонту; кожна така частинка має світову лінію, яка перетинається S ₁, і тому вона все ще на своєму шляху.

Малюнок 7.3.4.png — Малюнок\(\PageIndex{4}\) - На думку далекого спостерігача, чи коли-небудь впадає матерія досягає сингулярності?

S ₂ - ще один можливий «зараз» для того ж спостерігача одночасно. Згідно з цим визначенням «зараз», всі частинки пройшли горизонт подій, але жодна з них ще не потрапила в сингулярність. Нарешті, S ₃ - це «зараз», згідно з яким всі частинки потрапили в сингулярність.

Якби це була особлива відносність, то ми могли б вирішити, яка поверхня була правильним поняттям одночасності для спостерігача, виходячи зі стану руху спостерігача. Але в цілому відносність, це працює тільки локально (саме тому я зробив всі три поверхні збігаються біля E). Не існує чітко визначеного способу вирішити, який правильний спосіб глобального розширення цього поняття одночасності.

Хоча може здатися дивним, що ми не можемо сказати, чи сформована сингулярність «вже» за даними далекого спостерігача, це насправді просто неминучий результат того факту, що сингулярність схожа на космос. Те ж саме відбувається у випадку просторучасу Шварцшильда, який ми думаємо як опис вічної чорної діри, тобто тієї, яка завжди існувала і завжди буде. На подібній діаграмі Пенроуза для вічної чорної діри ми все ще можемо намалювати космічну поверхню, подібну до S ₁ або S ₂, представляючи визначення «зараз» таким чином, що сингулярність ще не існує.

Діаграми Пенроуза в цілому

В ідеалі ми хотіли б узагальнити процедуру малювання діаграм Пенроуза, щоб ми могли однозначно визначити одну для будь-якого простору-часу. Це виявляється не так вже й зрозуміло. Процедура пішла б приблизно так:

Зробіть n-мірний перетин або проекцію, де зазвичай, але не завжди, n = 2.
Зробіть перетворення, щоб зменшити отриманий многовид до плоского кінцевого розміру.
Примикають ідеалізовані поверхні і точки на нескінченності.

На кроці 1 ми хочемо скористатися будь-якими симетріями, такими як обертальна симетрія, щоб кінцевий результат був інформативним, був представником всього простору-часу і точно зобразив причинно-наслідкові зв'язки в початковому простору-часу. Якщо початковий проміжок часу має низький ступінь симетрії (наприклад, простір часу, що містить три чорні діри, розташовані трикутником), то для цього може знадобитися n > 2. На цьому кроці нам також потрібно переконатися, що світлоподібні геодезичні конструкції в початковому просторі належним чином відповідають світлоподібним геодезикам в підколекторі.

Для кроку 2 ми вже дали геометричну характеристику типу перетворення, який ми маємо на увазі, який називається конформним перетворенням. Виявляється можливим інкапсулювати цю ідею простим аналітичним способом. Враховуючи просторовий час з метрикою g, ми визначаємо фіктивну метрику\(\tilde{g} = \Omega^{2} g\), де\(\Omega\) є ненульове дійсне число, яке змінюється від точки до точки. (Cf. сек. 5.11, де\(\Omega\) була постійною.) Ідея тут полягає в тому, що g і\(\tilde{g}\) домовитися про те, де знаходиться світловий конус, але вони розходяться в вимірі відстаней і часу. Той самий колектор, оснащений фіктивною метрикою,\(\tilde{g}\) - це той, який малюється на сторінці, коли ми робимо діаграму Пенроуза. Ми дозволяємо\(\Omega\) → 0, коли ми наближаємося до ідеалізованих граничних областей\(\mathscr{I}^{+}\), таких як i ⁰ і, і це те, що змушує діаграму Пенроуза займати скінченний простір на сторінці.

Взагалі неможливо зробити те, що потрібно на кроці 2, зробивши конформне перетворення, щоб змінити колектор на плоский. Колектор, який може бути сплющений таким чином, називається конформально плоским. Всі двовимірні многовиди конформально плоскі, тому в випадку n = 2 це гарантовано. Для n > 3 ми зазвичай не матимемо конформної площинності, якщо присутні гравітаційні хвилі або приливні сили.

Найбільш проблемною частиною, на подив, є крок 3. Ця тема йде під загальною рубрикою «пограничні конструкції». Відгуки доступні на цю тему. ⁴ Існує ряд більш-менш специфічних методів побудови кордону, з алфавітним супом імен, включаючи g-boundary, c-boundary, b-boundary та a-boundary. Як у когось, хто не є фахівцем в цій підгалузі, складається враження, що це область досліджень, яка вийшла погано і ніколи не давала ніяких корисних результатів, але робота триває, і не виключено, що в якийсь момент дим очиститься. Як простий приклад того, що хотілося б отримати, але не виходить, з цих досліджень, здавалося б, природно запитати, скільки розмірів існує в чорній дірі сингулярності. (Дивіться приклад 4 для обговорення, чому це нетривіальне питання.) Різні відповіді повертаються з різних методів. Наприклад, b-граничний підхід говорить, що і чорна діра, і космологічні особливості є нульовими точками, тоді як в методі c-boundary (який був розроблений для гармонізації з діаграмами Пенроуза) вони є трьома поверхнями (як можна було б уявити з діаграм Пенроуза).

Глобальна гіперболічність

Причинність стосується нашого смутно визначеного почуття, що світ повинен мати впорядковане прогресування причини та наслідків. Зробити це поняття більш точним напрочуд важко. Діаграми Пенроуза та пов'язані з ними поняття по суті є уявленнями про причинно-наслідкову структуру простору-часу, і вони виявляються корисними для об'єднання однієї з найбільш задовольняючих спроб визначити причинно-наслідковий зв'язок. Це визначення називається глобальною гіперболічністю. Незрозуміла термінологія пов'язана з класифікацією рівнянь з частинними похідними.

Деякі визначення потрібні як попередні. Розглянемо набір S подій у просторовічасі. S обмежений, якщо він не включає жодної з ідеалізованих точок на діаграмі Пенроуза, які ми додали на нескінченності. ⁵ S закривається, якщо він містить власну межу. ⁶ S компактний, якщо він закритий і обмежений.

Нотатки

⁵ Більш суворо, це еквівалентно тому, що для будь-якого геодезичного в S існує пов'язаний афінний параметр.

⁶ Щоб зробити це більш точним, ми продовжуємо, як описано в розділі 5.10, збільшивши набір точок у нашому просторово-часовому колекторі M, щоб включити точки на нескінченно малих відстанях від однієї з початкових точок. Тоді S закривається, якщо для будь-якої точки в збільшеному варіанті S є точка, що лежить на нескінченно малій відстані від неї в початковому варіанті S.

Приклад 9: Компактні і некомпактні світлові конуси

На малюнку 7.3.5 показаний простор часу, що містить чорну діру, яка утворюється гравітаційним колапсом. Точка P знаходиться всередині горизонту подій, Q зовні. Розглянемо наступні чотири набори точок:

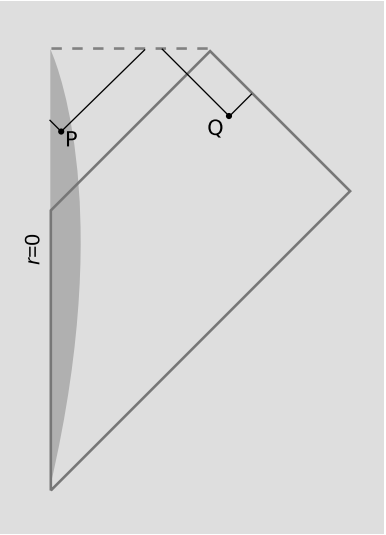
Малюнок 7.3.5.png — Малюнок\(\PageIndex{5}\)

I ⁺ (P), званий хронологічним майбутнім P, є внутрішньою частиною майбутнього світлового конуса P.

J ⁺ (P) схожий на I ⁺ (P), але також включає події, що знаходяться на межі світлового конуса, тобто події, які не можуть бути пов'язані з P часовою кривою, але які можуть бути пов'язані з нею світлоподібною кривою. Ми називаємо це причинним майбутнім П, так як саме сукупність подій, які могли бути викликані П.

I ⁺ (Q) і J ⁺ (Q) є аналогічними множинами, побудованими на Q.

З цих чотирьох комплектів компактний тільки J ⁺ (P). I ⁺ (P) є некомпактним, оскільки він не закритий. I ⁺ (Q) і J ⁺ (Q) некомпактні, оскільки вони не обмежені; вони включають ідеалізовані точки на нескінченності, які лежать в i ⁺ і\(\mathscr{I}^{+}\).

На додаток до позначень, представлених у прикладі 9, нам знадобляться аналогічні позначення I ⁻ і J ^- для відповідних минулих світлових конусів.

Визначення

Простір є глобально гіперболічним, якщо: (1) немає замкнутих часових кривих (КТК), ⁷ і (2) заданих будь-яких двох подій P і Q, перетин J ⁺ (P) і J ⁻ (Q) є компактним. (Умова 2 потрібно тільки тоді, коли P і Q є точками в многообразі, а не граничними точками.)

⁷ Для точності умова потрібно зробити трохи сильніше. Ми не хочемо закритих, не схожих на простір кривих, і ми також хочемо, щоб криві були неможливими для існування кривих, які довільно близькі до таких кривих, в тому сенсі, що для будь-якої події існує околиці навколо нього, які ніколи не можуть бути переглянуті.

У глобальному гіперболічному просторовічасі початкові задачі завжди мають унікальні рішення. Тобто ми можемо вибрати поверхню, подібну до простору, і дати значення хвилі на цій поверхні, і хвильове рівняння буде мати унікальне рішення. Така поверхня називається поверхнею Коші.

Ми можемо легко перевірити шляхом огляду диграм Пенроуза, що spacetimes, описані раніше в цьому розділі, глобально гіперболічні. Умова 2 передбачає, що перетин не містить жодних особливостей або точок на нескінченності. Хоча простори чорної діри містять особливості, космічна природа цих сингулярностей передбачає, що вони ніколи не можуть лежати в перетині світлових конусів, про які йдеться у визначенні. Тому такі простори є глобально гіперболічними.

Приклад 10: Глобальна гіперболічність

Малюнок 7.3.6a.png — Малюнок\(\PageIndex{6}\)

Малюнок 7.3.6b.png — Малюнок\(\PageIndex{6}\)

На малюнку 7.3.6 (1) зображений шматок, вирізаний з простору Мінковського. Пунктирний контур призначений для того, щоб вказати, що шматок не містить його межі. Цей простор часу не є глобально гіперболічним. Для певних варіантів подій P і Q перетин J ⁺ (P) J ⁻ (Q) може розтягнутися до розрізу на краю. Оскільки просторовий час не включає його межі, цей перетин не був би компактним. Легко зрозуміти, чому причинно-наслідковий зв'язок не вдається в цьому просторічасу. Якщо ми виберемо поверхню, подібну до простору, біля нижньої частини діаграми, вона прорізала б лише невелику частину нижньої частини простору-часу. У більш пізні часи просторовий час зростає зі швидкістю, яка більша за c Тому таку поверхню не можна використовувати як поверхню Коші; враховуючи початкові умови на цій поверхні, ми не можемо передбачити, що станеться в частинок Всесвіту, які знаходяться поза її причинним майбутнім.

На малюнку 7.3.6 (2) ми маємо той самий приклад, але тепер межа включена. Цей набір не є множиною, що виключає його з розгляду як простору-час у загальній теорії відносності. Малюнок 7.3.6 (3) являє собою зображення простору Мінковського з тимчасовою сингулярністю в ньому (пунктирною лінією). Сингулярності не є множинами точок у многообразі, тому топологічно, це схоже на простір Мінковського з єдиною часовою кривою хірургічно видаленої. Глобальна гіперболічність зазнає невдачі, оскільки перетин J ⁺ (P) J ⁻ (Q) може оточувати сингулярність і не буде компактним, оскільки воно не включало б її межі в сингулярності. Дане порушення глобальної гіперболічності свідчить про збій причинно-наслідкового зв'язку в такому просторовічасу (див. Розділ 6.3).

Відрізавши нижню половину алмазу, що представляє простір Мінковського, отримаємо рис. 7.3.6 (4). Пунктирна лінія вказує на те, що межа не включена, а значить, це множина. Він також глобально гіперболічний. Цей приклад говорить про те, що глобальна гіперболічність не обов'язково захоплює все, що ми могли б коли-небудь захотіти описати у визначенні причинно-наслідкового зв'язку. Якщо палеонтолог, який живе в цьому просторічасу, знайде викопне динозавра, вбудоване в скелю, вона, природно, зробить висновок, що динозавр жив у якийсь момент минулого, викликаючи існування викопного. Але, можливо, це не так - гіпотетичний динозавр міг би існувати до кордону. Це порушення причинно-наслідкового зв'язку зі смаком креаціонізму має інший смак, ніж ситуація, яку ми мали б, якби нижній край діаграми був особливістю великого вибуху; у цьому випадку у нас була б відома причина, чому ланцюги причин і наслідків не могли бути розширені назад у минуле за межі певний час.

Посилання

³ Див. також розділ 7.4

⁴ Ешлі, «Теореми про сингулярність та абстрактне побудова кордонів» digitalcollections.anu.edu.a... dle/1885/46055. ГарсіяПаррадо і Сеновілла, «Причинні структури та причинні межі», http://arxiv.org/abs/gr-qc/0501069.