3.2: Причинність та оборотність
- Page ID
- 97210
Хоча процес ковзної середньої порядку завжди\(q\) буде стаціонарним без умов на коефіцієнти\(\theta_1\)\(\ldots\)\(\theta_q\), деякі більш глибокі думки потрібні у випадку процесів AR (\(p\)) та ARMA (\(p,q\)). Для простоти почнемо з дослідження авторегресійного процесу порядку першого, який задається рівняннями\(X_t=\phi X_{t-1}+Z_t\) (запис\(\phi=\phi_1\)). Повторні ітерації дають, що
\[X_t =\phi X_{t-1}+Z_t =\phi^2X_{t-2}+Z_t+\phi Z_{t-1}=\ldots =\phi^NX_{t-N}+\sum_{j=0}^{N-1}\phi^jZ_{t-j}. \nonumber \]
Допускаючи\(N\to\infty\), тепер можна було б показати, що, з ймовірністю один,
\[ X_t=\sum_{j=0}^\infty\phi^jZ_{t-j} \tag{3.2.2} \]
є слабко стаціонарним розв'язком рівнянь AR (1) за умови, що\(|\phi|<1\). These calculations would indicate moreover, that an autoregressive process of order one can be represented as linear process with coefficients \(\psi_j=\phi^j\).
Приклад\(\PageIndex{1}\): Mean and ACVF of an AR(1) process
Оскільки авторегресивний процес порядку був ідентифікований як приклад лінійного процесу, можна легко визначити його очікуване значення як
\[ E[X_t]=\sum_{j=0}^\infty\phi^jE[Z_{t-j}]=0, \qquad t\in\mathbb{Z}. \nonumber \]
Для ACVF виходить, що
\ почати {вирівнювати*}
\ гамма (h)
&= {\ rm Cov} (X_ {t+h}, x_T)\\ [.2см]
&= Е\ ліворуч [\ sum_ {j=0} ^\ інфті\ Phi^jz_ {t+h-j}\ sum_ {k=0} ^\ fty\ phi^kz_ {t+h-j}\\ [.2см]
&=\ сигма^2\ сума_ {k=0} ^\ infty\ phi^ {k+h}\ phi^ {k}
=\ сигма ^ 2\ phi ^ h\ sum_ {k=0} ^\ infty\ phi ^ {2k}
=\ розриву {\ сигма^2\ phi^h} {1-\ phi^2},
\ end {вирівнювати*}
де\(h\geq 0\). This determines the ACVF for all \(h\) using that \(\gamma(-h)=\gamma(h)\). It is also immediate that the ACF satisfies \(\rho(h)=\phi^h\). See also Example 3.1.1 for comparison.
Приклад\(\PageIndex{2}\): Nonstationary AR(1) processes
У прикладі 1.2.3 ми ввели випадкову прогулянку як нестаціонарний часовий ряд. Його також можна розглядати як нестаціонарний процес AR (1) з параметром\(\phi=1\). Загалом авторегресивні процеси першого порядку з коефіцієнтами\(|\phi|>1\) називаються {\ it explusive}\/, бо вони не допускають слабко стаціонарного рішення, яке можна було б виразити як лінійний процес. Однак можна поступити наступним чином. Перепишіть визначальні рівняння процесу AR (1) як
\[ X_t=-\phi^{-1}Z_{t+1}+\phi^{-1}X_{t+1}, \qquad t\in\mathbb{Z}. \nonumber \]
Застосуйте зараз ті ж ітерації, що і раніше, щоб прийти до
\[ X_t=\phi^{-N}X_{t+N}-\sum_{j=1}^N\phi^{-j}Z_{t+j},\qquad t\in\mathbb{Z}. \nonumber \]
Відзначимо, що в слабо стаціонарному випадку справжнє спостереження було описано з точки зору минулих нововведень. Однак представлення в останньому рівнянні містить лише майбутні спостереження з відставаннями часу більшими за теперішній час\(t\). З статистичної точки зору це не має особливого сенсу, хоча за допомогою ідентичних аргументів, як зазначено вище, ми можемо отримати
\[ X_t=-\sum_{j=1}^\infty\phi^{-j}Z_{t+j}, \qquad t\in\mathbb{Z}, \nonumber \]
як слабо нерухомий розчин у вибухонебезпечному корпусі.
Результат попереднього прикладу призводить до поняття причинності, що означає, що процес\((X_t: t\in\mathbb{Z})\) має уявлення з точки зору білого шуму,\((Z_s: s\leq t)\) і це, отже, не корелює з майбутнім, як дано\((Z_s: s>t)\). Наведемо визначення для загального випадку АРМА.
Визначення: причинність
Процес ARMA (\(p,q\)), заданий (3.1.1) є причинним, якщо існує\((\psi_j: j\in\mathbb{N}_0)\) така послідовність, що\(\sum_{j=0}^\infty|\psi_j|<\infty\) і
\[ X_t=\sum_{j=0}^\infty\psi_jZ_{t-j}, \qquad t\in\mathbb{Z}. \nonumber \]
Причинність означає, що часовий ряд ARMA може бути представлений як лінійний процес. Раніше в цьому розділі було видно, як процес AR (1), коефіцієнт якого задовольняє умові,\(|\phi|<1\) може бути перетворений в лінійний процес. Також було показано, що це неможливо, якщо\(|\phi|>1\). Умови за авторегресійним параметром\(\phi\) можуть бути повторені через відповідний авторегресивний поліном\(\phi(z)=1-\phi z\) наступним чином. Він стверджує, що
\(|\phi|<1\) if and only if \(\phi(z)\not=0\) for all \(|z|\leq 1, \\[.2cm]\)
\(|\phi|>1\) if and only if \(\phi(z)\not=0\) for all \(|z|\geq 1\).
Виходить, що характеристика в терміні нулів авторегресивних поліномів переноситься від випадку AR (1) до загального випадку ARMA (\(p,q\)). Причому\(\psi\) -ваги результуючого лінійного процесу мають легке уявлення в терміні многочленів\(\phi(z)\) і\(\theta(z)\). Результат підсумовується в наступній теоремі.
Теорема 3.2.1
\((X_t: t\in\mathbb{Z})\)Дозволяти бути процес ARMA (\(p,q\)) такий, що\(\phi(z)\) многочлени і не\(\theta(z)\) мають спільних нулів. Тоді\((X_t\colon t\in\mathbb{Z})\) є причинним, якщо і тільки якщо\(\phi(z)\not=0\) для всіх\(z\in\mathbb{C}\) с\(|z|\leq 1\). Коефіцієнти\((\psi_j: j\in\mathbb{N}_0)\) визначаються розширенням рядів потужності.
\[ \psi(z)=\sum_{j=0}^\infty\psi_jz^j=\frac{\theta(z)}{\phi(z)}, \qquad |z|\leq 1. \nonumber \]
Поняття, тісно пов'язане з причинно-наслідковим зв'язком, - це оборотність. Це поняття мотивовано наступним прикладом, який вивчає властивості часового ряду ковзного середнього порядку 1.
Приклад\(\PageIndex{3}\)
\((X_t\colon t\in\mathbb{N})\)Дозволяти бути MA (1) процес з параметром\(\theta=\theta_1\). Це проста вправа для обчислення ACVF та ACF як
\[ \gamma(h)=\left\{ \begin{array}{l@{\quad}l} (1+\theta^2)\sigma^2, & h=0, \\ \theta\sigma^2, & h=1 \\ 0 & h>1, \end{array}\right. \qquad \rho(h)=\left\{ \begin{array}{l@{\quad}l} 1 & h=0.\\ \displaystyle\theta(1+\theta^2)^{-1}, & h=1. \\ 0 & h>1. \end{array}\right. \nonumber \]
Ці результати призводять до висновку, що\(\rho(h)\) не змінюється, якщо\(\theta\) параметр замінити на\(\theta^{-1}\). Більш того, існують пари\((\theta,\sigma^2)\), які ведуть до того ж АКВФ, наприклад\((5,1)\) і\((1/5,25)\). Отже, ми приходимо до того, що дві моделі MA (1)
\[ X_t=Z_t+\frac 15Z_{t-1},\qquad t\in\mathbb{Z}, \qquad (Z_t\colon t\in\mathbb{Z})\sim\mbox{iid }{\cal N}(0,25), \nonumber \]
і
\[ X_t=\tilde{Z}_t+5\tilde{Z}_{t-1},\qquad t\in\mathbb{Z}, \qquad (\tilde{Z}\colon t\in\mathbb{Z})\sim\mbox{iid }{\cal N}(0,1), \nonumber \]
не відрізняються, тому що ми спостерігаємо лише,\(X_t\) але не змінні шуму\(Z_t\) і\(\tilde{Z}_t\).
Для зручності, статистик підбере модель, яка задовольняє критерію оборотності, який буде визначено далі. Він вказує, що послідовність шумів може бути представлена як лінійний процес у спостереженнях.
Визначення: оборотність
Процес ARMA (\(p,q\)), заданий (3.1.1), є оборотним, якщо існує\((\pi_j\colon j\in\mathbb{N}_0)\) така послідовність, що\(\sum_{j=0}^\infty|\pi_j|<\infty\) і
\[ Z_t=\sum_{j=0}^\infty\pi_jX_{t-j},\qquad t\in\mathbb{Z}. \nonumber \]
Теорема 3.2.2
\((X_t: t\in\mathbb{Z})\)Дозволяти бути процес ARMA (\(p,q\)) такий, що\(\phi(z)\) многочлени і не\(\theta(z)\) мають спільних нулів. Тоді\((X_t\colon t\in\mathbb{Z})\) є оборотним якщо і тільки якщо\(\theta(z)\not=0\) для всіх\(z \in\mathbb{C}\) с\(|z|\leq 1\). Коефіцієнти\((\pi_j)_{j\in\mathbb{N}_0}\) визначаються розширенням рядів потужності.
\[ \pi(z)=\sum_{j=0}^\infty\pi_jz^j=\frac{\phi(z)}{\theta(z)}, \qquad |z|\leq 1. \nonumber \]
Відтепер передбачається, що всі послідовності ARMA, зазначені в продовженні, є причинно-наслідковими та зворотними, якщо явно не вказано інше. Заключний приклад цього розділу підкреслює корисність усталеної теорії. Він займається надмірністю параметрів та обчисленням послідовностей причинності та оборотності.\((\psi_j\colon j\in\mathbb{N}_0)\) and \((\pi_j\colon j\in\mathbb{N}_0)\).
Приклад\(\PageIndex{4}\): Parameter redundancy
Розглянемо рівняння ARMA
\[ X_t=.4X_{t-1}+.21X_{t-2}+Z_t+.6Z_{t-1}+.09Z_{t-2}, \nonumber \]
які, здається, генерують послідовність ARMA (2,2). Однак авторегресивний і ковзний середній поліноми мають загальний нуль:
\ почати {вирівнювати*}
\ тильда {\ phi} (z) &=1-.4z-.21z^2 =( 1-.7z) (1+.3z),\\ [.2см]
\ тильда {\ тета} (z) &=1+.6z+.09z^2 =( 1+.3z) ^2.
\ end {вирівнювати*}
Таким чином, можна скинути рівняння ARMA до послідовності порядку (1,1) і отримати
\[ X_t=.7X_{t-1}+Z_t+.3Z_{t-1}. \nonumber \]
Тепер відповідні многочлени не мають спільних коренів. Зверніть увагу, що коріння\(\phi(z)=1-.7z\) і\(\theta(z)=1+.3z\) є\(10/7>1\) і\(-10/3<-1\), відповідно. Таким чином, теореми 3.2.1 та 3.2.2 означають, що існують причинно-наслідкові та оборотні розв'язки. Далі відповідні коефіцієнти в розширеннях
\[ X_t=\sum_{j=0}^\infty\psi_jZ_{t-j} \qquad and \qquad Z_t=\sum_{j=0}^\infty\pi_jX_{t-j}, \qquad t\in\mathbb{Z}, \nonumber \]
розраховуються. Починаючи з послідовності причинно-наслідкових зв'язків\((\psi_j: j\in\mathbb{N}_0)\). Написання, для\(|z|\leq 1\),
\[ \sum_{j=0}^\infty\psi_jz^j =\psi(z) =\frac{\theta(z)}{\phi(z)} =\frac{1+.3z}{1-.7z} =(1+.3z)\sum_{j=0}^\infty(.7z)^j, \nonumber \]
його можна отримати з порівняння коефіцієнтів, які
\[ \psi_0=1 \qquad and \qquad \psi_j=(.7+.3)(.7)^{j-1}=(.7)^{j-1}, \qquad j\in\mathbb{N}. \nonumber \]
Аналогічно обчислюють коефіцієнти оборотності\((\pi_j: j\in\mathbb{N}_0)\) з рівняння.
\[ \sum_{j=0}^\infty\pi_jz^j =\pi(z) =\frac{\phi(z)}{\theta(z)} =\frac{1-.7z}{1+.3z} =(1-.7z)\sum_{j=0}^\infty(-.3z)^j \nonumber \]
(\(|z|\leq 1\)) як
\[ \pi_0=1 \qquad and \qquad \pi_j=(-1)^j(.3+.7)(.3)^{j-1}=(-1)^j(.3)^{j-1}. \nonumber \]
Разом попередні розрахунки поступаються явним уявленням
\[ X_t=Z_t+\sum_{j=1}^\infty(.7)^{j-1}Z_{t-j} \qquad and \qquad Z_t=X_t+\sum_{j=1}^\infty(-1)^j(.3)^{j-1}X_{t-j}. \nonumber \]
В іншій частині цього розділу надається загальний спосіб визначення ваг\((\psi_j\colon j\geq 1)\) для причинно-наслідкового процесу ARMA (\(p,q\)), заданого\(\phi(B)X_t=\theta(B)Z_t\), де\(\phi(z)\not=0\) для всіх\(z\in\mathbb{C}\) таких, що\(|z|\leq 1\). Оскільки\(\psi(z)=\theta(z)/\phi(z)\) для них вага\(\psi_j\) можна обчислити\(z\), зіставивши відповідні коефіцієнти в рівнянні\(\psi(z)\phi(z)=\theta(z)\), тобто
\[ (\psi_0+\psi_1z+\psi_2z^2+\ldots)(1-\phi_1z-\ldots-\phi_pz^p) = 1+\theta_1z+\ldots+\theta_qz^q. \nonumber \]
Рекурсивне рішення для\(\psi_0,\psi_1,\psi_2,\ldots\) дає
\ begin {align*}
\ psi_0&=1,\
\ psi_1-\ phi_1\ psi_0&=\ тета_1,\\ psi_2-
\ phi_1\ psi_1-\ phi_2\ psi_2\ psi_0&=\ theta_2,
\ end {align*}
і так далі до тих пір, поки\(j<\max\{p,q+1\}\). Загальне рішення можна заявити як
\[ \psi_j-\sum_{k=1}^j\phi_k\psi_{j-k}=\theta_j, \qquad 0\leq j<\max\{p,q+1\}, \tag{3.2.1}\\[.2cm] \]
\[ \psi_j-\sum_{k=1}^p\phi_k\psi_{j-k}=0, \qquad \phantom{0\leq} j\geq\max\{p,q+1\},\tag{3.2.2} \]
якщо ми визначимо,\(\phi_j=0\) якщо\(j>p\) і\(\theta_j=0\) якщо\(j>q\). Тому для отримання коефіцієнтів потрібно\(\psi_j\) розв'язати однорідне лінійне різницеве рівняння (3.2.2) з дотриманням початкових умов, зазначених у пункті (3.2.1). Докладніше про цю тему див. Розділ 3.6 Броквелла та Девіса (1991) та Розділ 3.3 Шумвей і Стоффер (2006).
R розрахунки
У R ці обчислення можна виконати за допомогою команди Armatoma. Наприклад, можна скористатися командами
> Арматома (ар = .7, ма = .3,25)
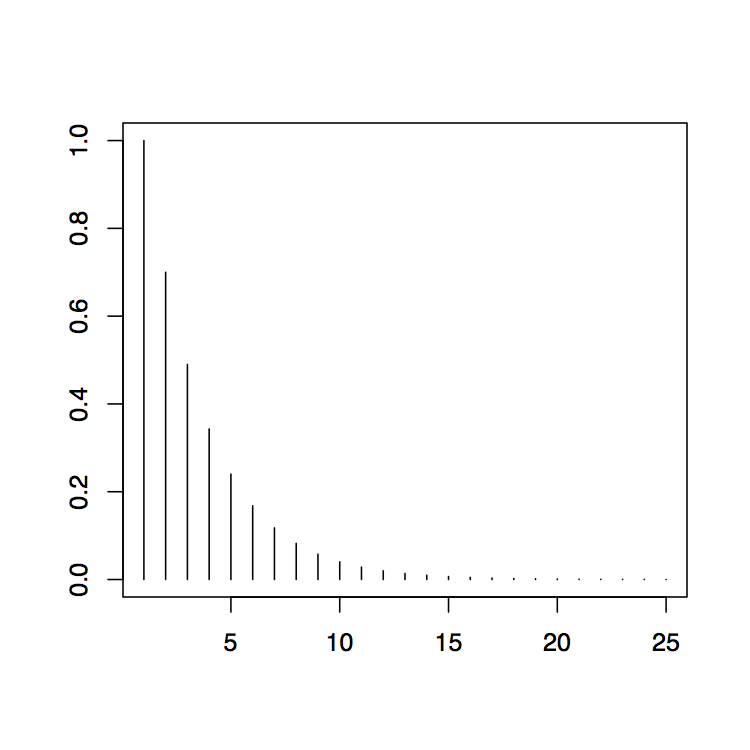
> сюжет (Арматома (ар = .7, ма = .3,25))
який дасть результат, показаний на малюнку 3.4. Сюжет добре показує експоненціальний розпад\(\psi\) -ваг, що характерно для процесів ARMA. У таблиці наведені рядні ваги\(\psi_0,\ldots,\psi_{24}\). Це включається вибором 25 в аргументі функції Armatoma.
| 1.00000000 | 0.7000000000 | 0.4900000000 | 0.3430 000 000 | 0.240 1000000 |
| 0.1680700000 | 0.1176490000 | 0.0823543 000 | 0.0576480100 | 0.0403536070 |
| 0.028245 249 | 0.01973 2674 | 0.0138412872 | 0.0096889010 | 0.0067822307 |
| 0.0047475615 | 0.0033232931 | 0.0023263051 | 0.0016284136 | 0.0011398895 |
| 0.0007979227 | 0.0005585459 | 0.0003909821 | 0,0002736875 |
0,0001915812 |