4.3: Чотири вектори (Частина 2)

Вектор частоти та релятивістський доплерівський зсув

У дусі індексно-гімнастичного позначення частота - це час, оскільки хвильове число k =\(\frac{1}{\lambda}\) - це простір, тому при обробці хвиль релятивістично природно здогадатися, що існує чотиричастотна f _a, зроблена шляхом складання (f, k), яка поводиться як вектор Лоренца. Це правильно, так як ми вже знаємо, що\(\partial_{a}\) перетворюється як коваріантний вектор, так і для скалярної хвилі форми

\[A = A_o \exp [2\pi if_ax^a]\]

оператор часткової похідної ідентичний множенню на 2\(\pi\) f _a.

Як додаток розглянемо релятивістський доплерівський зсув світлової хвилі. Для простоти давайте обмежимося одним просторовим виміром. Для світлової хвилі\(f = k\), так вектор частоти в розмірах 1+1 просто (f, f). Проводячи це через перетворення Лоренца, ми знаходимо

\[f' = (1 + v) \gamma f = \sqrt{\frac{1+v}{1-v}} f,\]

де друга форма більш чітко відображає симетричну форму релятивістських відносин, таку, що взаємозміна ролей джерела і спостерігача еквівалентна перегортанню знака v. Тобто релятивістська версія залежить тільки від відносного руху джерела і спостерігача, тоді як ньютонівський також залежить від руху джерела щодо середовища (тобто щодо бажаного кадру, в якому хвилі мають «правильну» швидкість). У ньютонівській механіці ми маємо f' = (1 + v) f для рухомого спостерігача. Відносно існує також тимчасове розширення коливань джерела, що забезпечує додатковий коефіцієнт\(\gamma\).

Цей аналіз розширений до 3+1 вимірів у задачі 11.

Приклад 15: Експерименти Айвс-Стілвелла

Релятивістський доплерівський зсув відрізняється від нерелятивістського коефіцієнтом розширення часу\(\gamma\), так що все ще існує зсув, навіть коли відносний рух джерела і спостерігача перпендикулярно напрямку поширення. Це називається поперечним доплерівським зрушенням. Ейнштейн запропонував це на початку як тест на відносність. Однак подібні експерименти важко проводити з високою точністю, оскільки вони чутливі до будь-якої похибки при вирівнюванні кута 90 градусів. Такі експерименти були врешті-решт проведені, з результатами, які підтвердили відносність, ⁷ але одновимірні вимірювання забезпечили як ранні випробування релятивістського доплерівського зсуву, так і найбільш точні на сьогоднішній день. Перший такий тест був зроблений Айвз і Стілвелл в 1938 році, використовуючи наступний трюк. релятивістський вираз

\[S_{v} = \sqrt{\frac{(1 + v)}{(1 − v)}}\]

для доплерівського зсуву має властивість, що

\[S_vS_{−v} = 1\]

що відрізняється від нерелятивістського результату

\[(1 + v)(1 − v) = 1 − v^2.\]

Таким чином, можна прискорити іон до релятивістської швидкості, виміряти як вперед доплеровскій зміщену частоту _f f і назад f _b, і обчислювати\(\sqrt{f_{f} f_{b}}\). Відповідно до відносності, це повинно точно дорівнювати частоті f _o, виміряної в кадрі спокою іона.

У особливо вишуканій сучасній версії ідеї Івс-Стілвелла ⁸ Saathoff et al. циркулювали іони Li ⁺ при v = .064 в кільці для зберігання. Для зменшення зміни швидкості між іонами в пучку використовувався електронно-охолоджувач. Оскільки ідентичність S _v S _−v = 1 не залежить від v, не потрібно було вимірювати v з такою ж неймовірною точністю, як частоти; потрібно було лише, щоб вона була стабільною та чітко визначеною. Природна ширина лінії становила 7 МГц, а інші експериментальні ефекти розширили її ще до 11 МГц. За допомогою кривої підгонки лінії вдалося досягти хороших результатів до декількох десятих частот МГц. Отримані частоти, в одиницях МГц, склали:

ф _ф = 582490203,44 ± 0,09

ф _б = 512671442,9 ± 0,5

\(\sqrt{f_{f} f_{b}}\)= 546466918,6 ± 0,3

f _o = 546466918,8 ± 0,4 (з попередньої експериментальної роботи)

Вражаюча згода з теорією зробила цей експеримент громовідводом для антивідносних поглядів.

Якщо шукати невеликі відхилення від прогнозів особливої відносності, природне місце для погляду - це високі швидкості. Експерименти IvessTilwell проводилися на швидкостях до 0,84, і вони підтверджують особливу відносність. ⁹

---

⁷ Див., наприклад, Хасселкамп, Мондрі та Шарман, Zeitschrift fur Фізика А: адрони та ядра 289 (1979) 151.

⁸ G. Saathoff та ін., «Покращений тест розширення часу в відносності», Фіз. Преподобний Літт. 91 (2003) 190403. Загальнодоступний опис експерименту наведено в кандидатській дисертації Саатоффа, www.mpi-hd.mpg.de/ato/homes/saathoff/ diss-saathoff.pdf.

⁹ Макартур та співавт., Фіз. Преподобний Літт 56 (1986) 282 (1986)

2

Раніше ми показали, що святкується E = mc ² випливає безпосередньо з форми перетворення Лоренца. Альтернативне виведення було дано Ейнштейном в одній з його класичних робіт 1905 року, в якій викладено теорію спеціальної відносності; стаття коротка, і відтворена англійською мовою в додатку А цієї книги. Заклавши основу чотиривекторних і релятивістських доплерівських зрушень, можна навести ще більш короткий варіант аргументу Ейнштейна. Обговорення також впорядковується шляхом обмеження обговорення розмірами 1+1 та викликом фотонів.

Припустимо, що ліхтар, в стані спокою в лабораторному кадрі, невагомо плаває в космічному просторі, і одночасно випромінює два імпульси світла в протилежних напрямках, кожен з енергією\(\frac{E}{2}\) і частотою f. шляхом симетрії імпульси скасовується, а ліхтар залишається в стані спокою. Спостерігач в русі зі швидкістю v щодо лабораторії бачить частоти пучків, зміщених в f' = (1 ± v)\(\gamma\) f Вплив на енергії пучків можна знайти чисто класично, шляхом перетворення електричного і магнітного полів в рухому кадрі, але як ярлик ми можемо застосувати кванто- механічне відношення E _ph = hf для енергій фотонів, що складають пучки. Результатом є те, що рухомий спостерігач знаходить сумарну енергію пучків не E, а (\(\frac{E}{2}\)) (1 + v)\(\gamma\) + (\(\frac{E}{2}\)) (1 − v)\(\gamma\) = E\(\gamma\).

Обидва спостерігачі сходяться на думці, що ліхтар повинен був витратити частину енергії, що зберігається в його паливі, щоб зробити два імпульси. Але рухомий спостерігач каже, що крім цієї енергії Е була ще одна енергія Е (\(\gamma\)− 1). Звідки могла з'явитися ця енергія? Він повинен був виходити від кінетичної енергії ліхтаря. Швидкість ліхтаря залишалася постійною протягом усього експерименту, тому це зниження кінетичної енергії, яке спостерігав рухомий спостерігач, мабуть, відбулося внаслідок зменшення інерційної маси ліхтаря - звідси назва статті Ейнштейна: «Чи залежить інерція тіла від його енергетичного вмісту?»

Щоб з'ясувати, скільки маси втратив ліхтар, ми повинні вирішити, як ми можемо навіть визначити масу в цьому новому контексті. У ньютонівській механіці ми мали K = (\(\frac{1}{2}\)) mv ², і за принципом відповідності це все одно повинно триматися в межі низьких швидкостей. Розширюючи E (\(\gamma\)− 1) у ряді Тейлора, ми знаходимо, що вона дорівнює E (\(\frac{v^{2}}{2}\)) +., і в границі низьких швидкостей це повинно бути таким же\(\Delta K = (\frac{1}{2}) \Delta mv^{2}\), як і, тому\(\Delta\) m = E. Повторно вставляючи коефіцієнти c, щоб повернутися до нерелятивістських одиниць, ми маємо E =\(\Delta\) mc ².

Неприклад: електричні та магнітні поля

Досить легко помітити, що електричне та магнітне поля не можуть бути космічними частинами двох чотирьох векторів. Розглянемо розташування, показане на малюнку 4.2.2 (1). У нас є два нескінченні поїзди рухомих зарядів, накладених на одну лінію, і один заряд поруч з лінією. Незважаючи на те, що лінійні заряди, утворені двома поїздами, рухаються в протилежних напрямках, їх струми не скасовуються. Негативний заряд, що рухається вліво, робить струм, який йде вправо, тому в кадрі 1 загальний струм вдвічі більше, ніж сприяв будь-який лінійний заряд.

Малюнок\(\PageIndex{2}\) - Магнетизм - це чисто релятивістський ефект.

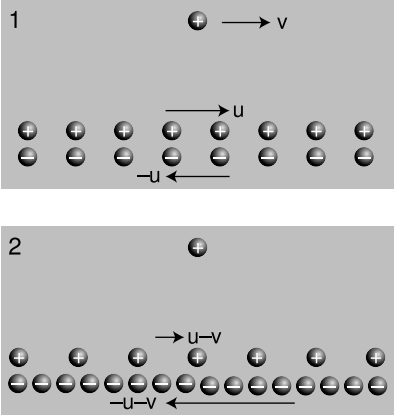
У кадрі 1 щільність заряду двох лінійних зарядів скасовується, і електричне поле, яке відчуває одиночний заряд, тому дорівнює нулю. Кадр 2 показує, що ми побачили б, якби ми спостерігали все це з системи відліку рухається разом з самотнім зарядом. Обидва лінійні заряди знаходяться в русі в обох системах відліку, але в кадрі 1 лінійні заряди рухалися з однаковими швидкостями, тому їх скорочення Лоренца були рівними, а щільність заряду скасована. У кадрі 2, однак, їх швидкості нерівні. Позитивні заряди рухаються повільніше, ніж в кадрі 1, тому в кадрі 2 вони менше скорочуються. Негативні заряди рухаються швидше, тому їх скорочення зараз більше. Оскільки щільність заряду не скасовується, в кадрі 2 є електричне поле, яке вказує на провід, залучаючи самотній заряд.

У нас тут є логічне протиріччя, тому що спостерігач у кадрі 2 пророкує, що заряд зіткнеться з проводом, тоді як в кадрі 1 виглядає так, ніби він повинен рухатися з постійною швидкістю паралельно проводу. Експерименти показують, що заряд дійсно стикається з проводом, тому для підтримки Лоренц-інваріантності електромагнетизму ми змушені винаходити новий вид взаємодії, один між рухомими зарядами і іншими рухомими зарядами, що викликає прискорення в кадрі 2. Це магнітна взаємодія, і якби ми про неї ще не знали, ми були б змушені її придумати. Тобто магнетизм - це чисто релятивістський ефект. Причина релятивістського ефекту може бути досить сильним, щоб приклеїти магніт до холодильника, полягає в тому, що він порушує делікатне скасування надзвичайно великих електричних взаємодій між електрично нейтральними об'єктами.

Хоча приклад показує, що електричні та магнітні поля перетворюються, коли ми переходимо від одного кадру до іншого, легко показати, що вони не трансформуються як космічні частини релятивістського чотиривекторного. Це відбувається тому, що перетворення між рамами 1 і 2 відбувається уздовж осі, паралельної дроту, але впливає на складові полів перпендикулярно проводу. Електромагнітне поле фактично перетворюється як тензор 2 рангу.

Електромагнітний потенціал Чотири вектора

Електромагнітна величина, яка перетворюється як чотири-вектор, є потенціалом. У розділі 3.7 я згадав той факт, який може бути або не може бути вам знайомий, що тоді як поляризаційні властивості ньютонівського гравітаційного поля дозволяють описати його за допомогою одного скалярного потенціалу\(\phi\) або одного векторного поля\(\textbf{g} = − \nabla \phi\), пари електромагнітних поля (E, B) потребують пари потенціалів,\(\boldsymbol{\Phi}\) а А. Легко помітити, що не\(\boldsymbol{\Phi}\) може бути скаляром Лоренца. Електричний заряд q є скаляром, тому\(\boldsymbol{\Phi}\) якби також скаляр, то добуток q\(\boldsymbol{\Phi}\) був би скаляром. Але це дорівнює енергії зарядженої частинки, яка є лише часоподібною складовою енергії-імпульсу чотиривекторного, а тому не самим скалером Лоренца. Це протиріччя,\(\boldsymbol{\Phi}\) тому не скаляр.

Щоб побачити, як\(\boldsymbol{\Phi}\) вписатися в відносність, розглянемо нерелятивістське квантово-механічне відношення q\(\boldsymbol{\Phi}\) = hf для зарядженої частинки в потенціалі\(\boldsymbol{\Phi}\). Оскільки f є часовим компонентом чотирьох векторів відносності, ми повинні\(\boldsymbol{\Phi}\) бути часовим компонентом деяких чотирьох векторів, Ab. Для просторової частини цього чотири-вектора, давайте напишемо A, так що\(A_{b} = (\boldsymbol{\Phi}, \textbf{A})\). За наступним аргументом ми бачимо, що цей таємничий А повинен мати щось спільне з магнітним полем.

Розглянемо приклад малюнка 4.2.3 з квантово-механічної точки зору. Заряджена частинка q має хвильові властивості, але скажімо, що її можна добре наблизити в цьому прикладі як слідувати певній траєкторії. Це схоже на наближення променів до хвильової оптики. Світловий промінь у класичній оптиці слідує принципу Ферма, також відомому як принцип найменшого часу, який стверджує, що шлях променя від точки А до точки Б - це той, який екстремізує довжину оптичного шляху (по суті кількість коливань). Причина цього в тому, що променеве наближення - це лише наближення. Промінь насправді має деяку ширину, яку ми можемо візуалізувати як пучок сусідніх траєкторій. Тільки якщо траєкторія буде слідувати принципу Ферма, втручання між сусідніми шляхами буде конструктивним. Класична довжина оптичного шляху знаходить шляхом інтеграції k · ds, де k - хвильове число. Щоб зробити це релятивістським, нам потрібно використовувати чотиривекторний частоту для формування f _b ^{dx b}, який також може бути виражений як f _b ^{v b} d\(\tau\) =\(\gamma\) (f − k · v) d\(\tau\). Якщо заряд знаходиться в стані спокою і магнітних полів немає, то величина в дужках є\(f = \frac{E}{h} = (\frac{q}{h}) \Phi\). Правильне релятивістське узагальнення явно f _b = (\(\frac{q}{h}\)) A _b.

Малюнок\(\PageIndex{3}\) - Заряджена частинка слідує траєкторії, яка екстремізує\(\int\) f _b dx ^b порівняно з іншими сусідніми траєкторіями. Відносно траєкторію слід розуміти як світову лінію в 3+1-мірному просторовічасі.

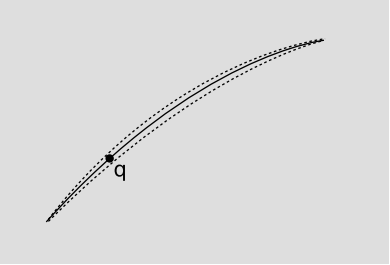
Оскільки космічна частина Ab, A, призводить до швидкозалежних ефектів, ми робимо висновок, що А - це свого роду потенціал, який відноситься до магнітного поля, так само, як потенціал\(\boldsymbol{\Phi}\) відноситься до електричного поля. A відомий як векторний потенціал, а зв'язок між потенціалами та полями є

\[\begin{split} \textbf{E} &= - \nabla \Phi - \frac{\partial \textbf{A}}{\partial t} \\ \textbf{B} &= \nabla \textbf{A} \ldotp \end{split}\]

Відмінне обговорення векторного потенціалу з чисто класичної точки зору дається в класичних лекціях Фейнмана. ¹⁰ На малюнку 4.2.4 показаний приклад.

Малюнок\(\PageIndex{4}\) - Магнітне поле (зверху) і векторний потенціал (знизу) соленоїда. Нижня схема знаходиться в площині, що прорізає талію соленоїда, на що вказує пунктирна лінія на верхній схемі. Для нескінченного соленоїда магнітне поле рівномірне зсередини і нуль зовні, тоді як векторний потенціал пропорційний r зсередини і зовні.\(\frac{1}{r}\)

Посилання

¹⁰ Лекції Фейнмана з фізики, Фейнман, Лейтон та Сендс, Еддісон Уеслі Лонгман, 1970