2.6: Загальний конічний розділ

Рівняння\[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \label{2.7.1} \tag{2.7.1}\]

являє собою еліпс, велика вісь якого знаходиться вздовж\(x\) осі, а центр якого знаходиться біля початку координат. Але що робити, якщо його центр знаходиться не на початку, а якщо велика вісь знаходиться під деяким кутом нахилу до\(x\) осі? Яким буде рівняння, яке представляє такий еліпс? Малюнок\(\text{II.37}\).

\(\text{FIGURE II.37}\)

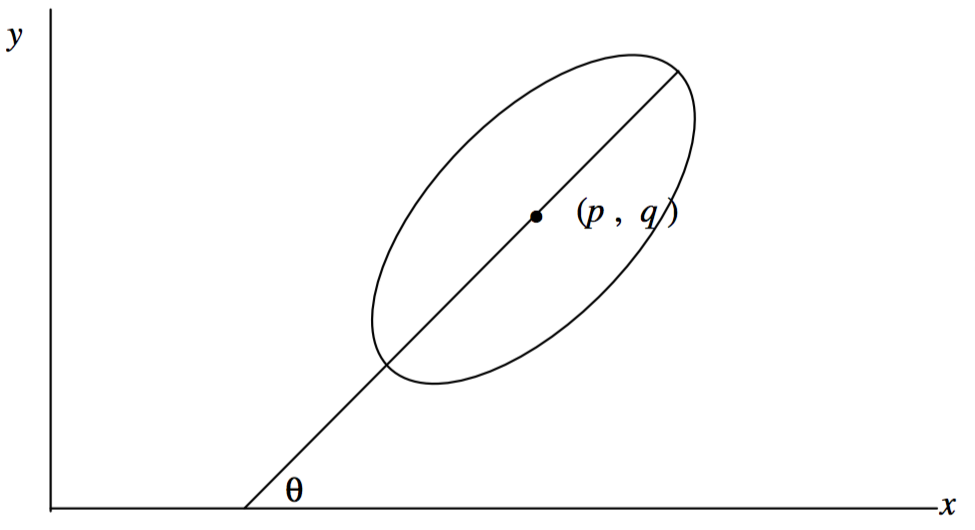
Якщо центр перекладено від початку до точки\((p, q)\), рівняння, що представляє еліпс, буде знайдено\(x\) шляхом заміни на\(x − p\) і\(y\) на\(y − q\). Якщо велика вісь нахилена під кутом θ до\(x\) осі, рівняння, що представляє еліпс, буде знайдено\(x\) шляхом заміни на\(x \cos θ + y \sin θ\) і\(y\) на\(−x \sin θ + y \cos θ\). У будь-якому випадку, якщо еліпс перекладено або повернуто або обидва,\(x\) і кожен\(y\) буде замінений лінійними виразами в\(x\) і\(y\), і результуюче рівняння матиме не більше членів в\(x^2 , \ y^2 , \ xy, \ x, \ y\) і константу. Те ж саме стосується параболи або гіперболи. Таким чином, будь-яка з цих трьох кривих буде представлена рівнянням виду

\[ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0. \label{2.7.2} \tag{2.7.2}\]

(Коефіцієнти\(a\) і не\(b\) є напіввеликими і напівнезначними осями.) Мабуть випадкові позначення коефіцієнтів виникають тому, що ці цифри є площинними ділянками тривимірних поверхонь (еліпсоїда, параболоїду та гіперболоїду), які описуються термінами, що включають координату, а\(z\) також\(x\) і\(y\). Звичайні позначення для цих тривимірних поверхонь дуже систематичні, але коли терміни в\(z\) видаляються для двомірного випадку, очевидно, випадкові позначення\(a, \ b, \ c, \ f, \ g, \ h\) залишаються. У будь-якому випадку вищевказане рівняння можна розділити на постійний член без втрати загальності, так що рівняння до еліпса, параболи або гіперболи можна записати, якщо це бажано, як

\[ax^2 + 2hxy + by^2 + 2gx + 2fy + 1 = 0. \label{2.7.3} \tag{2.7.3}\]

Чи вірно зворотне? Тобто, чи завжди рівняння цієї форми обов'язково являє собою еліпс, параболу або гіперболу?

Не зовсім. Наприклад,

\[6x^2 + xy - y^2 - 17x - y + 12 = 0 \label{2.7.4} \tag{2.7.4}\]

являє собою дві прямі лінії (її можна розрахувати на два лінійних члени - спробуйте), в той час як

\[2x^2 -4xy + 4y^2 -4x + 4 = 0 \label{2.7.5} \tag{2.7.5}\]

задовольняє тільки один пункт. (Знайдіть його.)

Однак плоский переріз конуса може бути двома лініями або однією точкою, тому, можливо, тепер ми можемо запитати, чи має загальне рівняння другого ступеня завжди представляти конічний переріз. Відповідь: близько, але не зовсім.

Наприклад,

\[4x^2 + 12xy + 9y^2 + 14x + 21y + 6 = 0 \label{2.7.6} \tag{2.7.6}\]

являє собою дві паралельні прямі, в той час як

\[x^2 + y^2 + 3x + 4y + 15 = 0 \label{2.7.7} \tag{2.7.7}\]

не може бути задоволений жодним реальним\((x,y)\).

Однак площина може перетинати циліндр по двох паралельних прямих, або по одній прямій, або зовсім немає. Тому, якщо ми розтягнемо визначення конуса дещо, щоб включити циліндр як особливий обмежувальний випадок, то можна сказати, що\(y\) загальне рівняння другого ступеня в\(x\) і дійсно завжди представляє конічний переріз.

Чи є якісь засоби, за допомогою яких можна сказати поглядом на певне рівняння другого ступеня, наприклад

\[8x^2 + 10xy -3y^2 -2x - 4y - 2 = 0, \label{2.7.8} \tag{2.7.8}\]

який тип конічного перерізу представлений? Відповідь - так, і ця буває гіперболою. Дискримінація проводиться шляхом вивчення властивостей детермінанта

\ begin {масив} {l | c c c |}
& a & h & g\\
\ Дельта = & h & b & f\\
& g & f & c\\
\ мітка {2.7.9}\ тег {2.7.9}
\ кінець {масив}

Я розробив таблицю після дизайну дихотомічних таблиць, які зазвичай використовуються таксономами в біології, в якій користувач стикається з куплетом (або іноді триплетом) альтернатив, а потім направляється до наступної частини таблиці. Я позбаву читача від виведення таблиці; замість цього я опишу її використання.

У таблиці я використовував символ,\(\bar{a}\) щоб означати кофактор\(a\) в\(\bar{h}\) детермінанті, кофактор\(h\),\(\bar{g}\) кофактор\(g\), і т.д. явно, це

\[\bar{a} = bc - f^2 , \label{2.7.10} \tag{2.7.10}\]
\[\bar{b} = ca - g^2 , \label{2.7.11} \tag{2.7.11}\]
\[\bar{c} = ab - h^2 , \label{2.7.12} \tag{2.7.12}\]
\[\bar{f} = gh - af , \label{2.7.13} \tag{2.7.13}\]
\[\bar{g} = hf - bg \label{2.7.14} \tag{2.7.14}\]
і\[\bar{h} = fg - ch . \label{2.7.15} \tag{2.7.15}\]

Перший стовпець позначає вибір, який користувачеві пропонується зробити. На початку є два варіанти,\(1\) і другий стовпець говорить, що це\(1^\prime\) за вибір, а четвертий стовпець говорить, куди йти далі. Таким чином, якщо визначник дорівнює нулю, перейдіть до\(2\); в іншому випадку переходите до\(5\). Якщо в стовпці є зірочка\(4\), ви закінчили. Колонка\(3\) говорить, який тип конічного розділу ви прибули, і стовпець\(5\) дає приклад.

Незалежно від типу конічного перерізу, координати його центру є,\((\bar{g}/\bar{c}, \ \bar{f}/\bar{c} )\) а кут,\(θ\) який робить його велика або поперечна вісь з віссю x, задається

\[\tan 2θ = \frac{2h}{a-b}. \label{2.7.16} \tag{2.7.16}\]

Таким чином, якщо\(x\) спочатку замінюється на\(x + \bar{g} / \bar{c}\) і\(y\) з\(y + \bar{f}/\bar{c}\), а потім нове\(x\) замінюється на\(x \cos θ − y \sin θ\) і нове\(y\) на\(x \sin θ + y \cos θ\), Рівняння прийме звичну форму конічного перерізу з його великою або поперечною віссю збігається з\(x\) вісь і її центр біля початку. Будь-які його властивості, такі як ексцентриситет, потім можна вивести зі знайомих Рівнянь. Ви повинні спробувати це за допомогою Equation\(\ref{2.7.8}\).

Ключ до конічних перерізів

Зіткнувшись із загальним рівнянням другого ступеня в\(x\) і\(y\), мені часто здається зручним прямо на початку обчислити значення кофакторів з рівнянь 2.7.10 − 2.7.15.

Ось вправа, яку ви, можливо, хотіли б спробувати. Показати, що еліпс\(ax^2 + 2hxy + by^2 + 2gx + 2fy + 1 = 0\) міститься всередині прямокутника, сторони якого

\[x = \frac{\bar{g} \pm \sqrt{\bar{g}^2 - \bar{a} \bar{c}}}{\bar{c}} \label{2.7.18} \tag{2.7.18}\]

\[y = \frac{\bar{f} \pm \sqrt{\bar{f}^2 - \bar{b} \bar{c}}}{\bar{c}} \label{2.7.19} \tag{2.7.19}\]

Іншими словами, ці чотири лінії є вертикальною і горизонтальною дотичними до еліпса.

Це, мабуть, не дуже корисно в небесній механіці, але, ймовірно, буде корисно при вивченні еліпсів Ліссажу або параметрів Стокса поляризованого світла. Це також корисно в програмуванні комп'ютера для малювання, наприклад, еліпса\(14x^2 - 4xy + 11y^2 - 44x -58y + 71 = 0\). Для цього ви, ймовірно, захочете почати з деякого значення\(x\) і обчислити два відповідних значення\(y\), а потім перейти до іншого значення\(x\). Але з якого значення\(x\) слід починати? Рівняння\(\ref{2.7.18}\) підкаже вам.

Але що означають Рівняння\(\ref{2.7.18}\) і\(\ref{2.7.19}\) означають, якщо конічний переріз Рівняння не\(ax^2 + 2hxy + by^2 + 2gx + 2fy + 1 = 0\) є еліпсом? Вони як і раніше корисні, якщо конічний розріз є гіперболою. Рівняння\(\ref{2.7.18}\) і\(\ref{2.7.19}\) все ще вертикальні і горизонтальні тангенси - але в цьому випадку гіпербола повністю виходить за межі, накладені цими дотичними. Якщо осі гіперболи горизонтальні і вертикальні, то одне чи інше рівняння\(\ref{2.7.18}\) і\(\ref{2.7.19}\) вийде з ладу.

Якщо конічний перетин є параболою, рівняння\(\ref{2.7.18}\) і не\(\ref{2.7.19}\) корисні, тому що\(c = 0\). Існує тільки один горизонтальний тангенс і тільки один вертикальний тангенс. Вони даються

\[x = \frac{\bar{a}}{2\bar{g}} \label{2.7.20} \tag{2.7.20}\]

і\[y = \frac{\bar{b}}{2\bar{f}} \tag{2.7.21} \label{2.7.21}\]

Якщо вісь параболи горизонтальна або вертикальна, то одне чи інше рівняння\(\ref{2.7.20}\) і\(\ref{2.7.21}\) вийде з ладу.

Якщо рівняння другого ступеня представляє одну або дві прямі лінії, або точку, або нічого, я думаю, що всі рівняння\(\ref{2.7.18}\) -\(\ref{2.7.21}\) зазнають невдачі - якщо, можливо, рівняння не представляє горизонтальні або вертикальні лінії. Я не розглядав це; можливо, читач хотів би це зробити.

Ось проблема, яку ви, можливо, хотіли б спробувати. Рівняння\(8x^2 + 10xy - 3y^2 - 2x - 4y - 2 = 0\) являє собою гіперболу. Що таке рівняння до його осей, до його асимптотів та сполучених гіпербол? Або, загалом, якщо\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0\) являє собою гіперболу, що таке рівняння до її осей, до її асимптотів та до її сполучених гіпербол?

Перш ніж почати, один момент, який варто відзначити, полягає в тому, що початкова гіпербола, її асимптоти та сполучена гіпербола) мають один\(g\) і\(f\) той же центр, що означає, що і однакові для кожного, і вони мають однакові осі\(a\), що означає\(h\), що, і\(b\) однакові для кожен. Відрізняються вони лише постійним терміном.

Якщо ви зробите першу проблему\(8x^2 + 10xy - 3y^2 - 2x - 4y -2 = 0\), буде досить багато числової роботи, щоб зробити. Коли я це зробив, я не використовував ні олівець і папір, ні калькулятор для рук. Швидше я сидів перед комп'ютером, роблячи числові розрахунки з твердженням Фортрана для кожного етапу обчислення. Я не думаю, що міг би зробити це інакше, не зробивши багато помилок. Найперше, що я зробив, це відпрацювати кофактори\(\bar{a}, \ \bar{h}, \ \bar{b}, \ \bar{g}, \ \bar{f}, \ \bar{c}\) і зберігати їх в комп'ютері, а також\((x_0, y_0)\) координати центру гіперболи, які задаються\(x_0 = \bar{g}/\bar{c}, \ y_0 = \bar{f} / \bar{c}\).

Незалежно від того, чи робите ви конкретну числову задачу, або більш загальну алгебраїчну, я пропоную вам діяти наступним чином. По-перше, віднесіть гіперболу до набору координат, походження\(x^\prime , y^\prime\) яких збігається з осями гіперболи. Робиться це шляхом заміни на\(x^\prime + x_0\) і\(x\)\(y\) с\(y' + y_0\). Це призведе до Рівняння форми\(ax^{\prime 2} + 2hx^\prime y^\prime + by^{\prime 2} + c^\prime = 0\). Коефіцієнти квадратичних членів будуть незмінними, лінійні члени зникнуть, а постійний термін зміниться. На цьому етапі я потрапив, для числового прикладу,\(8x^{\prime 2} + 10x^\prime y^\prime - 3y^{\prime 2} - 1.8163 = 0\).

Тепер віднесіть гіперболу до набору координат, осі\(x^{\prime \prime}, y^{\prime \prime}\) яких паралельні осям гіперболи. Це досягається\(x^\prime\) заміною на\(x^{\prime \prime} \cos θ − y^{\prime \prime} \sin θ\) і\(y^\prime\) з\(x^{\prime \prime} \sin θ + y^{\prime \prime} \cos θ\), де\(\tan 2θ = 2h /(a − b)\). Тут буде невелика проблема, тому що це дає два значення\(θ\) відрізняються\(90^\circ\), і ви хочете вирішити, який з них ви хочете. У будь-якому випадку результатом буде рівняння виду\(a^{\prime \prime} x^{\prime \prime 2} + b^{\prime \prime} y^{\prime \prime 2} + c^\prime = 0\), в якому\(a^{\prime \prime}\) і\(b^{\prime \prime}\) знаходяться протилежного знака. Крім того, якщо вам трапиться зрозуміти значення шуму «слід матриці інваріантний при ортогональному перетворенні», ви зможете перевірити арифметичні помилки, зазначивши це\(a^{\prime \prime} + b^{\prime \prime} = a + b\). Якщо це не так, ви допустили помилку. Крім того, постійний член повинен бути незмінним обертанням (зверніть увагу на одне просте на\(c\)). На цьому етапі я потрапив\( 9.933 x^{\prime \prime 2} - 4.933y^{\prime \prime 2} - 1.8163 = 0\). (Все це було зроблено з твердженнями Fortran на комп'ютері - ніякого фактичного розрахунку або запису, зробленого мною - і цифри зберігалися в комп'ютері до багатьох значущих цифр).

У будь-якому випадку це рівняння можна записати в знайомій формі\(\dfrac{x^{\prime \prime 2}}{A^2}-\dfrac{y^{\prime \prime 2}}{B^2}=1\), яку в даному випадку я зробив бути\(\dfrac{x^{\prime \prime 2}}{0.4283^2}-\dfrac{y^{\prime \prime 2}}{0.6088^2}=1\). Ми зараз на знайомій землі. Осі гіперболи є\( x^{\prime \prime} = 0\) і\(y^{\prime \prime} = 0\), асимптоти є\(\dfrac{x^{\prime \prime 2}}{A^2} - \dfrac{y^{\prime \prime 2}}{B^2} = 0\) і сполучена гіпербола є\(\dfrac{x^{\prime \prime 2}}{A^2} - \dfrac{y^{\prime \prime 2}}{B^2} = -1\).

Тепер, починаючи з\(\dfrac{x^{\prime \prime 2}}{A^2} - \dfrac{y^{\prime \prime 2}}{B^2} = -1\) для асимптотів, або з\(\dfrac{x^{\prime \prime 2}}{A^2} - \dfrac{y^{\prime \prime 2}}{B^2} =-1\) для сполучених гіперболи, ми зворотний процес. Ми переходимо до одногрунтованим координатам шляхом заміни на\(x^\prime \cos θ + y^\prime \sin θ\) і\(x^{\prime \prime}\)\(y^{\prime \prime}\) з −\(x^\prime \sin θ + y' \cos θ\), а потім до вихідних координат\(x^\prime\) заміною на\(x − x_0\) і\(y^\prime\) з\(y − y_0\).

Ось що я знаходжу:

Оригінальна гіпербола:\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0\)

Кон'югатна гіпербола:\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c_{\text{conj}} = 0,\)
де\(c_{\text{conj}} = -(2g \bar{g} + 2f \bar{f} + c \bar{c})/ \bar{c} = -(2gx_0 + 2fy_0 + c).\)

Асимптоти:\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c_{\text{asymp}} = 0,\)
де\(c_{\text{asymp}}\) можна записати в будь-якій з наступних еквівалентних форм:
\[c_{\text{asymp}} = + (a \bar{g}^2 + 2h \bar{g} \bar{f} + b \bar{f}^2 ) / \bar{c}^2 = ax_0^2 + 2hx_0 y_0 + by_0^2 = -(g \bar{g} + f \bar{f}) / \bar{c} .\]
[Остання з цих трьох форм може бути виведена дуже швидко, нагадавши, що умова для загального рівняння другого ступеня в\(x\) і\(y\) представляти дві прямі є те, що визначник\(∆\) повинен дорівнювати нулю. Погляд на цей детермінант покаже, що це означає, що\(g\bar{g} + f\bar{f} + c\bar{c} = 0.\)]

Осі гіпербол:\((y - x \tan θ - y_0 + x_0 \tan θ) ( y + x \cot θ - y_0 - x_0 \cot θ) = 0,\)
де\( \tan 2 θ = 2h / (a-b) . \)

Приклад:

Оригінальна гіпербола:\(8x^2 + 10xy - 3y^2 - 2x - 4y - 2 = 0\)

Кон'югатна гіпербола:\(8x^2 + 10xy - 3y^2 - 2x - 4y + \frac{80}{49} = 0\)

Асимптоти:\(8x^2 + 10xy - 3y^2 - 2x -4y - \frac{9}{49} = 0 , \)
які також можна записати\((4x - y - \frac{9}{7})(2x + 3y + \frac{1}{7}) = 0\)

Осі гіпербол:\(( y − 0.3866x + 0.3275)( y + 2.5866 x − 0.4613)\).

Вони показані на малюнку нижче - оригінальна гіпербола чорного кольору, сполучена синім кольором.

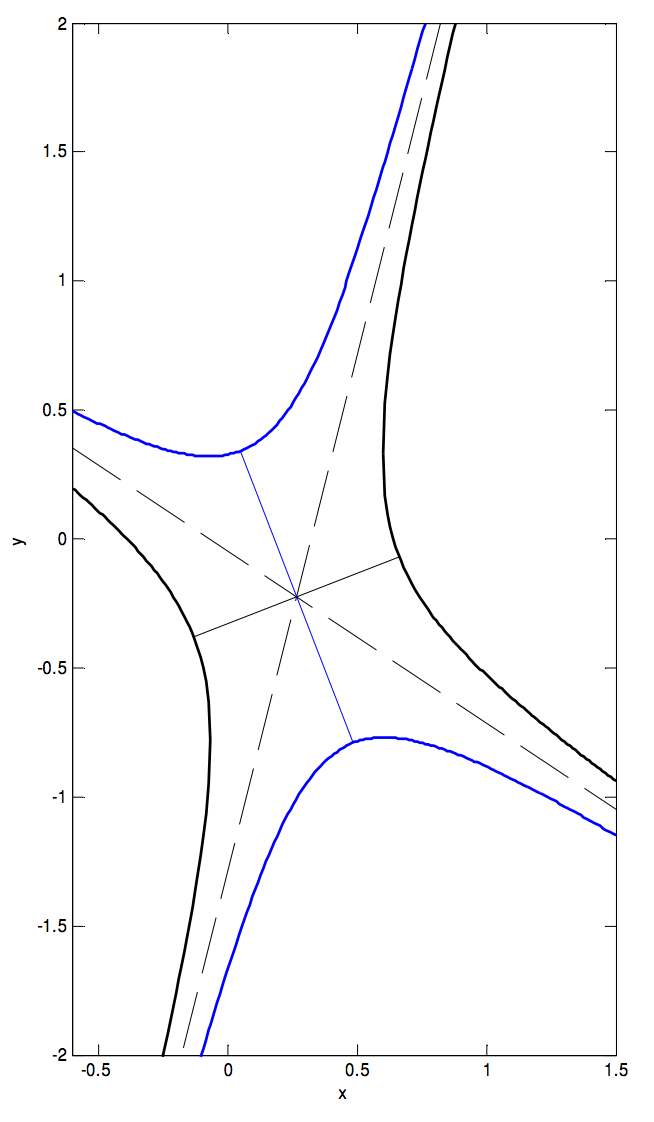
Центр знаходиться за адресою (0.26531, −0.22449).

Схили двох асимптотів - 4 і\(−\frac{2}{3}\). З рівняння 2.2.16 ми знаходимо, що тангенс кута між асимптотами є таким чином\(\tan 2ψ = \frac{14}{5}\)\(2ψ = 70^\circ .3\), і кут між асимптотою та великою віссю вихідної гіперболи є\(54^\circ .8\), або\(\tan ψ = 1.419\). Це дорівнює (див. Рівняння 2.5.3 і 2.5.10)\(\sqrt{e^2 - 1}\), тому ексцентриситет вихідної гіперболи є\(1.735\). З розділу 2.2, коротко Рівняння 2,5,6, ми незабаром виявимо, що ексцентриситет сполученої гіперболи є\(\csc ψ = 1.223\).

Мені виникає цікаве питання. Ми виявили,\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0\) що якщо гіпербола, то Рівняння до спряженої гіперболи та асимптотів мають подібну форму, а саме\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c_{\text{conj}} = 0\) і\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c_{\text{asymp}} = 0\), і ми знайшли вирази для\(c_{\text{conj}}\) і\(c_\text{asymp}\). Але що робити\(ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0\), якщо не гіпербола? Що робити, якщо це еліпс? Що представляють інші рівняння, враховуючи, що еліпс не має ні сполучених, ні асимптотів?

Наприклад,\(14x^2 - 4xy + 11y^2 - 44x -58y + 71 = 0\) це еліпс. Що таке\(14x^2 - 4xy + 11y^2 - 44x - 58y + 191 = 0\) і\(14x^2 -4xy + 11y^2 - 44x - 58y + 131 = 0\)? Я використав ключ на сторінці 47, і він сказав мені, що перше з цих рівнянь не задовольняється жодними реальними точками, що, на мою думку, є способом рівняння сказати мені, що немає такого поняття, як сполучений до еліпса. Друге рівняння повинно було бути «асимптотами», але ключ показує мені, що рівняння задовольняється лише однією реальною точкою, а саме (2, 3), яка збігається з центром вихідного еліпса. Я цього не очікував. Чи повинен був я це зробити?