Skip to main content
LibreTexts - Ukrayinska

2.5: Конічні перерізи

  1. Last updated
  2. Save as PDF
  • Page ID
    77860

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    До цих пір ми визначили еліпс, параболу та гіперболу без будь-якого посилання на конус. Багато читачів будуть знати, що плоский переріз конуса - це або еліпс, парабола або гіпербола, залежно від того, чи є кут, який площина робить з основою конуса, меншим, рівним або більшим за кут, який робить генератор конуса своїм підставою. Однак, враховуючи наведені нами визначення еліпса, параболи та гіперболи, потрібно доказ того, що вони насправді є конічними перерізами. У цей момент також можна згадати, що плоский переріз кругового циліндра також є еліпсом. Також, звичайно, якщо площина паралельна підставі конуса, або перпендикулярна осі циліндра, еліпс зводиться до кола.

    альт
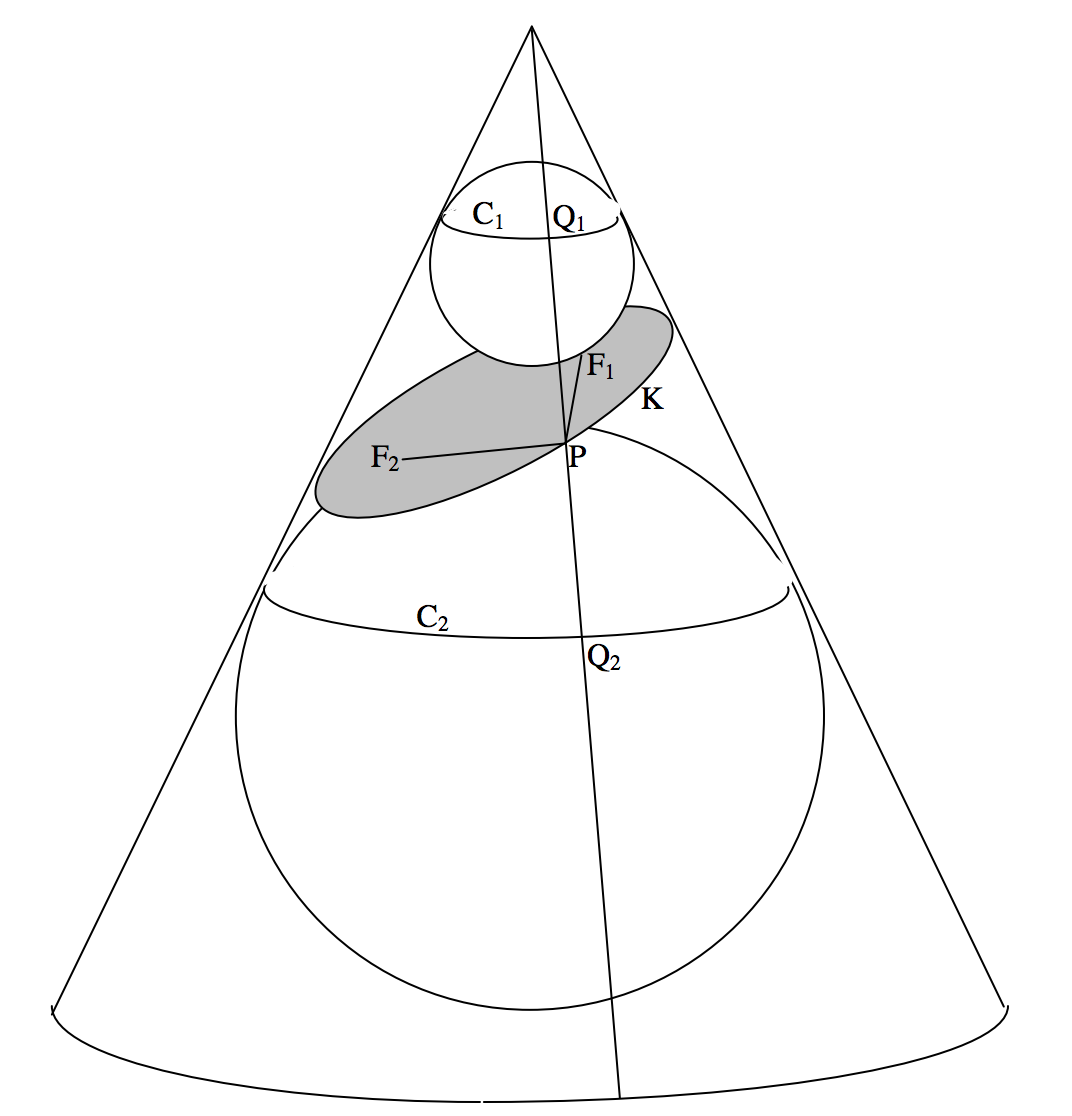
    \(\text{FIGURE II.36}\)

    Просте і чудове доказ можна привести в класичному Евклідове «Дана. Обов'язково. Будівництво. Доказ. Q.E.D.» стиль.

    Доказ

    Дано: Конус і площина такі, що кут, який робить площина з основою конуса, менше кута, який робить генератор конуса своїм підставою, а площина розрізає конус по замкнутій кривій\(\text{K}\). Малюнок\(\text{II.36}\).

    Потрібно: Довести, що\(\text{K}\) це еліпс.

    Конструкція: Побудуйте сферу над площиною, яка торкається конуса всередині кола\(\text{C}_1\) та площині в точці\(\text{F}_1\). Побудуйте також сферу під площиною, яка торкається конуса всередині кола\(\text{C}_2\) і площині в точці\(\text{F}_2\).

    Приєднайте точку\(\text{P}\) на кривій\(\text{K}\) до\(\text{F}_1\) і до\(\text{F}_2\).
    Намалюйте генератор, який проходить через точку\(\text{P}\) і який перетинається\(\text{C}_1\) в\(\text{Q}_1\) і\(\text{C}_2\) в\(\text{Q}_2\).

    Доказ:\(\text{PF}_1 = \text{PQ}_1\) (Дотичні до сфери від зовнішньої точки.)

    \(\text{PF}_2 = \text{PQ}_2\)(Дотичні до сфери від зовнішньої точки.)

    \(\therefore \text{PF}_1 + \text{PF}_2 = \text{PQ}_1 + \text{PQ}_2 = \text{Q}_1 \text{Q}_2\)

    і\(\text{Q}_1\text{Q}_2\) не залежить від положення\(\text{P}\), так як це відстань між колами\(\text{C}_1\) і\(\text{C}_2\) вимірюється вздовж генератора.

    \[\therefore \ \text{K is an ellipse and } \text{F}_1 \text{ and } \text{F}_2 \text{ are its foci}. \tag{Q.E.D.}\]

    Подібний аргумент покаже, що плоский переріз циліндра також є еліпсом.

    Читач також може розробити креслення, які покаже, що плоский переріз конуса, паралельного генератору, є параболою, і що площина крутіша, ніж генератор, розрізає конус в гіперболі. Малюнки найпростіше зробити папером, олівцем, циркулем і лінійкою, і зажадають деякої кмітливості. Хоча я бачив вищевказане доказ еліпса в декількох книгах, я не бачив відповідних доказів для параболи та гіперболи, але їх справді можна зробити, і читач повинен знайти це цікавим викликом. Якщо читач може використовувати комп'ютер, щоб зробити малюнки і може зробити краще, ніж мої погані зусилля з фігурою\(\text{II.36}\), він/вона досить добре з комп'ютером, що є ознакою неправильно витраченої молодості.