2.4: Гіпербола

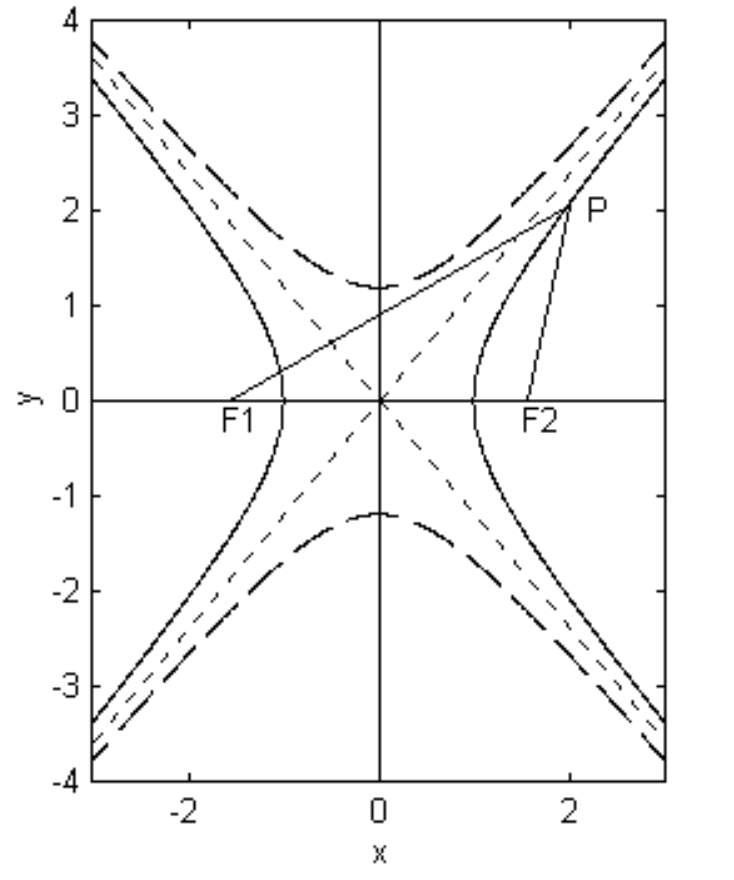
Гіпербола - це локус точки, яка рухається таким чином, що різниця між її відстанями від двох нерухомих точок, званих вогнищами, постійна. Назвемо різницю між цими двома відстанями$2a$ і відстанню між вогнищами$2ae$, де$e$ - ексцентриситет гіперболи, і є числом більше 1. Див$\text{II.28}$. Малюнок.

$\text{FIGURE II.28}$

Наприклад, в експерименті Янга з подвійною щілиною інтерференції яскрава бахрома розташована в точці на екрані таким чином, що різниця шляху для променів з двох щілин дорівнює$m$ довжинам хвиль.$m$ Коли екран переміщується вперед або назад, це співвідношення продовжує утримуватися для яскравої$m$ бахроми, локус якої між прорізами та екраном, отже, є гіперболою. Система радіолокаційної навігації «Decca», вперше використовувана на посадках D-Day у Другій світовій війні і виведена з експлуатації лише в 2000 році через те, що вона застаріла системою «GPS» (Global Positioning Satellite), залежала від цієї властивості гіперболи. (З моменту написання цього, частина системи Decca була повторно введена в експлуатацію як резервна у разі проблем з GPS.) Два радіолокаційні передавачі на деякій відстані будуть одночасно передавати радіолокаційні імпульси. Корабель отримає два сигнали, розділені коротким інтервалом часу, залежно від різниці між відстанями від корабля до двох передавачів. Це розмістило корабель на певній гіперболі. Корабель також слухав би іншу пару передавачів, і це поставило б корабель на другу гіперболу. Це потім розмістило корабель в одній з чотирьох точок, де дві гіперболи перетиналися. Зазвичай було б очевидно, який з чотирьох пунктів був правильним, але будь-яка неоднозначність може бути вирішена сигналами від третьої пари передавачів.

На$\text{II.28}$ малюнку координати$F_1$ і$F_2$ є, відповідно,$(−ae , 0)$ і$(ae , 0)$.

Умова$\text{PF}_1 − \text{PF}_2 = 2a$ вимагає, щоб

$$\left[ (x + ae)^2 + y^2 \right]^{\dfrac{1}{2}} - \left[ (x-ae)^2 + y^2 \right]^{\dfrac{1}{2}} = 2a, \label{2.5.1} \tag{2.5.1}$$

і це рівняння до гіперболи. Після деякої домовленості про це можна написати

$$\dfrac{x^2}{a^2} - \dfrac{y^2}{a^2 (e^2 -1)} = 1, \label{2.5.2} \tag{2.5.2}$$

яка є більш звичною формою для Рівняння до гіперболи. Визначимо довжину$b$ по

$$b^2 = a^2 (e^2 - 1). \label{2.5.3} \tag{2.5.3}$$

Рівняння тоді стає

$$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1, \label{2.5.4} \tag{2.5.4}$$

яка є найбільш звичною формою для Рівняння до гіперболи.

Приклад 1

Коли метеорит проходить по небу, його можна відстежити за допомогою радара. Радіолокаційні прилади можуть визначати дальність (відстань) метеороїда в залежності від часу. Покажіть, що, якщо метеороїд рухається з постійною швидкістю (сумнівне припущення, оскільки воно повинно сповільнюватися, але, можливо, ми можемо припустити, що зниження швидкості незначне під час спостереження), і якщо дальність$r$ побудована проти часу, графік буде гіперболою. Покажіть також, що, якщо$r^2$ покладений проти$t$, графік буде параболою форми

$$r^2 = a t^2 + bt + c,$$

де$a=V^2 , \ b = -2V^2 t_0, \ c = V^2 t_0^2 + r_0^2, \ V = \text{speed of the meteoroid}, \ t_0 = \text{time of closest approach}, \ r_0 = \text{distance of closest approach}$.

Радіолокаційне спостереження метеора дає наступні дані дальності часу:

\ begin {масив} {c l}
t (\ текст {s}) & r (\ текст {км})\\
\
0.0 & 101.4\ *\\
0.1 & 103.0\\
0.2 & 105.8\\
0.3 & 107.8\\
0.4 & 111.1\\
0.5 & 112,6\\
0.6 & підсилювач; 116,7\\
0,7 & 119.3\\
0.8 & 123,8\ *\
0.9 & 126.4\\
1.0\\
1.1 & 133.3\\
1.2\\
1.3 & 141.3\\\\
\ кінець {масив}

Припустимо, що швидкість метеора постійна.

Визначити i. час найближчого наближення (до 0,01$\text{s}$)
ii. Відстань найближчого підходу (до 0,1$\text{km}$)
iii. Швидкість (до 1.0$\text{km s}^{-1}$)

При бажанні просто використовуйте три зірочки дані, щоб визначити$a$,$b$ і$c$. Якщо ви енергійніше, використовуйте всі дані, і визначте$a$,$b$ і$c$ по найменших квадратах, і ймовірні похибки$V$,$t_0$ і$r_0$.

Відстань між двома вершинами гіперболи є її поперечною віссю, а довжина напівпоперечної осі$a$ - але яке геометричне значення довжини$b$? Про це йдеться нижче в наступному підрозділі (про сполучену гіперболу) і знову в більш пізньому розділі про параметр впливу.

Лінії, перпендикулярні$x$ -осі і проходять через вогнища, є двома латеральними прямими. Оскільки вогнища знаходяться в$(\pm ae , \ 0)$, точки, де латеральна пряма кишка перетинається гіпербола, можна знайти,$x = ae$ ввівши в Рівняння гіперболі, і тоді виявляється, що довжина$l$ напівширокої прямої кишки дорівнює

$$l = a(e^2 -1 ) . \label{2.5.5} \tag{2.5.5}$$

Визначення: Кон'югатна гіпербола

Рівняння

$$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = -1 \label{2.5.6} \tag{2.5.6}$$

- Рівняння до спряженої гіперболи.

Спряжена гіпербола намальована пунктирною на малюнку$\text{II.28}$, і видно, що геометричне значення$b$ полягає в тому, що це довжина напівпоперечної осі сполученої гіперболи. Проста справа показати, що ексцентриситет сполученої гіперболи є$e/\sqrt{e^2-1}$.

Визначення: Асимптоти

Лінії $$y = \pm \dfrac{bx}{a} \label{2.5.7} \tag{2.5.7}$$

є асимптотами гіперболи.

Також можна записати рівняння\ ref {2.5.7}

$$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 0. \label{2.5.8} \tag{2.5.8}$$

Таким чином

$$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = c \label{2.5.9} \tag{2.5.9}$$

це гіпербола, асимптоти або кон'югатна гіпербола, якщо$c = +1$,$0$ або$−1$ відповідно. Асимптоти малюються пунктирними лініями на малюнку$\text{II.28}$.

Напівавтоматичний кут ψ між асимптотами задається

$$\tan ψ = b/a. \label{2.5.10} \tag{2.5.10}$$

Вправа 1

Якщо ексцентриситет гіперболи є$e$, покажіть, що ексцентриситет її сполученого є$\dfrac{e}{\sqrt{e^2 - 1}}$.

Вправа 1: Слідство

Ніхто не здивується, зазначивши, що з цього випливає, що, якщо ексцентриситети гіперболи і її сполученого рівні, то кожен дорівнює$\sqrt{2}$.

Директори

Лінії$y = \pm a / e$ - це директриси, і, як і у випадку з еліпсом (і з аналогічним доказом), гіпербола має властивість, що відношення відстані$\text{PN}$ до фокусу до відстані до директриси постійне і дорівнює ексцентриситету гіперболи.$\text{PF}_2$ Це співвідношення (тобто ексцентриситет) менше одиниці для еліпса, рівне одиниці для параболи, і більше одиниці для гіперболи. Це не властивість, яка матиме велике значення для наших цілей, але варто згадати, оскільки це властивість, яка іноді використовується для визначення гіперболи. Я залишаю читачеві малювати дирекції в їх правильних позиціях на малюнку$\text{II.28}$.

Параметричні рівняння до гіперболи.

Читач згадає, що точка$(a \cos E, b \sin E)$ знаходиться на еліпсі$(x^2/a^2) + \left( y^2/b^2 \right) = 1$ і що це очевидно, тому що це рівняння є$E$ -елімінант$x = a \cos E$ і$y = b \sin E$. Кут$E$ має геометричну інтерпретацію як ексцентрична аномалія. Так само, згадуючи відношення$\cosh^2 \phi − \sinh^2 \phi = 1$, буде очевидно, що також$(x^2 / a^2) - \left(y^2/b^2 \right) = 1$ можна отримати як$\phi$ −елімінант рівнянь

$$x = a \cosh \phi, \quad y = b \sinh \phi \label{2.5.11} \tag{2.5.11}$$

Ці два рівняння, отже, параметричні рівняння до гіперболи, і будь-яка точка, що задовольняє ці два рівняння, лежить на гіперболі. Змінна не$\phi$ є кутом і не має геометричної інтерпретації, аналогічної ексцентричної аномалії еліпса. Рівняння

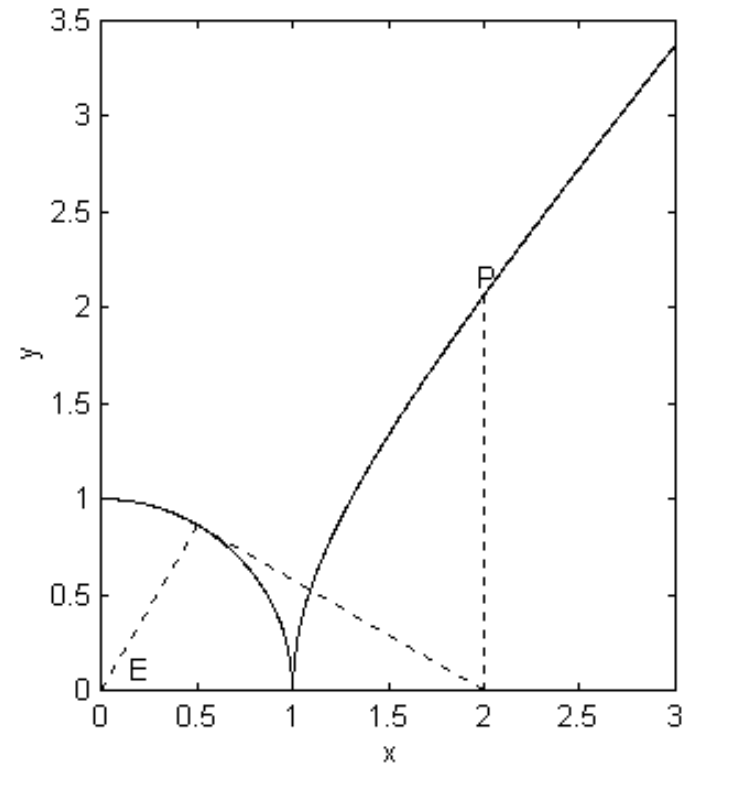
$$x = a \sec E, \quad y = b \tan E \label{2.5.12} \tag{2.5.12}$$

може також використовуватися як параметричні рівняння до гіперболи, за рахунок тригонометричної ідентичності$1 + \tan^2 E = \sec^2 E$. У цьому випадку кут$E$ має геометричну інтерпретацію (хоча і не особливо цікаву) стосовно допоміжної окружності, яка є окружністю радіуса a з центром у початку. Значення кута повинно проявлятися з малюнка$\text{II.29}$, в якому$E$ знаходиться ексцентричний кут, відповідний точці$\text{P}$.

$\text{FIGURE II.29}$

Параметр впливу

Частинка, що рухається дуже швидко під дією оберненої квадратної привабливої сили (наприклад, міжзоряного метеороїда або комети - якщо є такі речі - проходить повз Сонце, або електрона поблизу позитивно зарядженого атомного ядра) буде рухатися гіперболічним шляхом. Доводимо це в наступному розділі, а також обговорюємо необхідну швидкість. Ми можемо уявити, що частинка спочатку наближається з великої відстані вздовж асимптоти в правому нижньому куті фігури$\text{II.30}$. Коли він наближається до фокусу, він більше не рухається уздовж асимптоти, а вздовж руки гіперболи.

$\text{FIGURE II.30}$

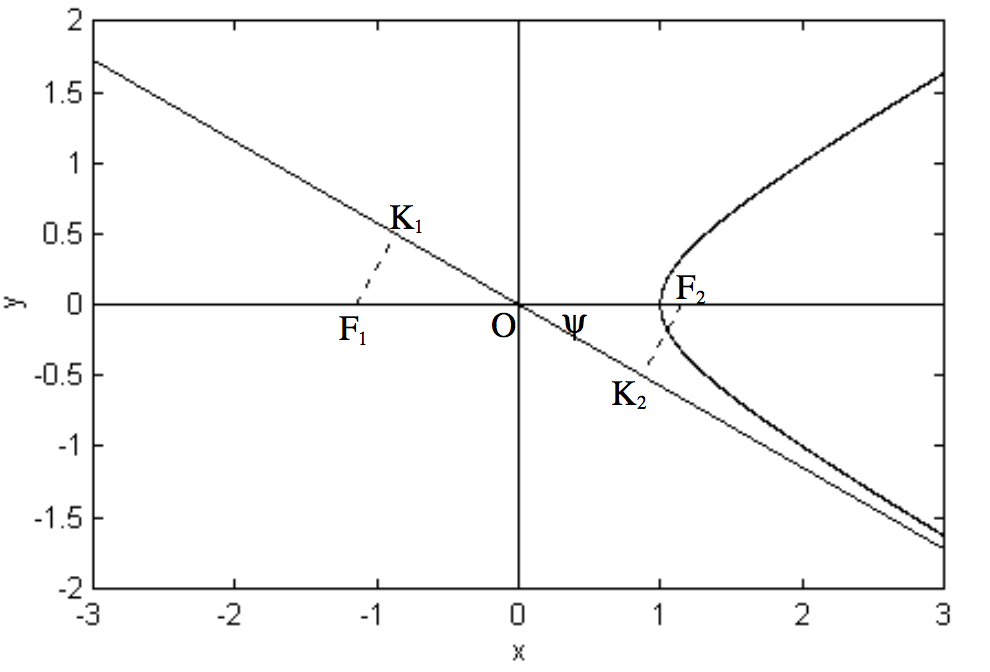
Відстань$\text{K}_2 \ \text{F}_2$, яка є відстань, на яку частка пропустила б$\text{F}_2$ за відсутності сили притягання, прийнято називати параметром удару. Так само, якби сила була силою відштовхування (наприклад, припустимо, що рухома частинка була позитивно зарядженою частинкою, і там був центр відштовхування в$\text{F}_1$,$\text{F}_1\text{K}_1$ буде параметром удару. Ясно,$\text{F}_1\text{K}_1$ і$\text{F}_2\text{K}_2$ рівні по довжині. Символ, який часто використовується в теорії розсіювання, будь то в небесній механіці або у фізиці частинок, є$b$ - але чи це$b$$b$ те саме, що йде в Рівняння до гіперболи і яке дорівнює півмажорній осі сполученої гіперболи?

$\text{OF}_2 = ae$, і тому$\text{K}_2\text{F}_2 = ae \sin ψ$. Це, у поєднанні з$\tan ψ = b/a$ і$b^2 = a^2 (e^2 − 1)$, незабаром покаже, що параметр впливу дійсно той самий$b$, з яким ми знайомі, і$b$ це, отже, дуже підходящий символ для використання для параметра впливу.

Дотичні до гіперболи

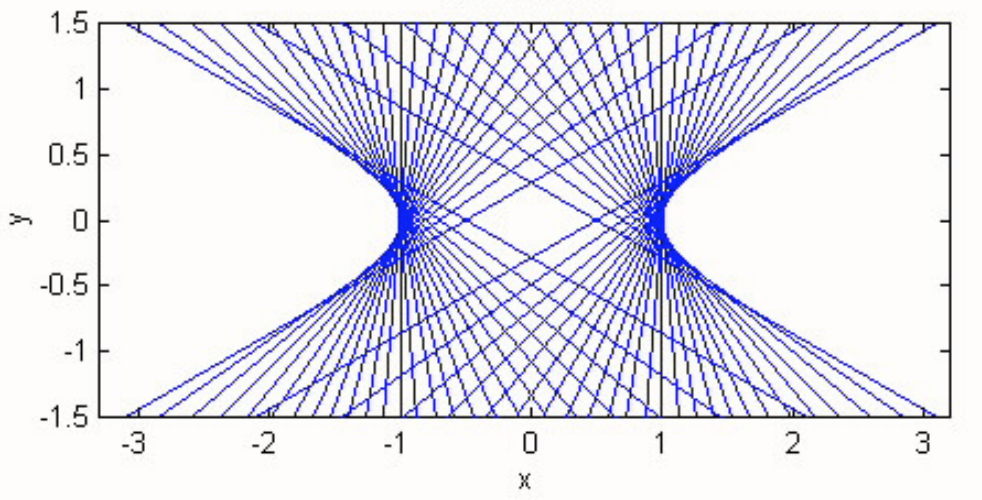
Використовуючи ті ж аргументи, що і для еліпса, читач повинен легко знайти ці рядки форми

$$y = mx \pm \sqrt{a^2 m^2 - b^2} \tag{2.5.13} \label{2.5.13}$$

дотичні до гіперболи. Це проілюстровано$\text{II.33}$ на малюнку для гіперболи з$b = a /2$, з дотичними, намальованими з нахилами$30^\circ$ до$150^\circ$ з кроком$5^\circ$. (Асимптоти мають$ψ = 26^\circ 34^\prime$.) (Вибачте, але немає цифр$\text{II.31}$ або$\text{II.32}$ - проблеми з комп'ютером!)

$\text{FIGURE II.31}$

Так само з аналогічних аргументів, що використовуються для еліпса, дотична до гіперболи в точці$(x ,y)$ виявляється

$$\frac{x_1x}{a^2} - \dfrac{y_1y}{b^2} = 1. \label{2.5.14} \tag{2.5.14}$$

Коло режисера

Що стосується еліпса, то і при подібному виведенні, місцем перетину точок перетину перпендикулярних дотичних є коло, званий директорської окружністю, яка має радіус$√(a^2 − b^2 )$. Це не має особливого значення для наших цілей, але читач, який зацікавлений, може захотіти довести це тим же методом, як це було зроблено для керівного кола еліпса, і може захотіти спробувати намалювати коло і деякі дотичні. Якщо$b > a$, тобто, якщо$ψ > 45^\circ$ і кут між асимптотами більше$90^\circ$, ніж, директорське коло не є реальним, і, звичайно, неможливо намалювати перпендикулярні дотичні.

Прямокутна гіпербола

Якщо кут між асимптотами є$90^\circ$, гіперболу називають прямокутної гіперболою. Для такої гіперболи ексцентриситет є$b = a$$√2$, директорське коло - це точка, а саме початок, а перпендикулярні дотичні можуть бути проведені тільки з асимптотів.

Рівняння прямокутної гіперболи є

$$x^2 - y^2 = a^2 \label{2.5.15} \tag{2.5.15}$$

і асимптоти знаходяться$45^\circ$ на$x$ осі.

$\text{O}x^\prime, \ \text{O}y^\prime$Дозволяти бути набір осей$45^\circ$ на$x$ осі. (Тобто вони є асимптотами прямокутної гіперболи.) Тоді рівняння прямокутної гіперболи, що відноситься до її асимптотів як координатних осей, знаходить підстановками.

$$\pmatrix{x \\ y} = \pmatrix{\cos 45^\circ & \sin 45^\circ \\ - \sin 45^\circ & \cos 45^\circ} \pmatrix{x^\prime \\ y^\prime} \tag{2.5.16} \label{2.5.16}$$

в$x^2 − y^2 = a^2$. Це призводить до рівняння

$$x^\prime y^\prime = \frac{1}{2} a^2 = c^2 , \quad \text{where} \quad c= a/\sqrt{2}, \label{2.5.17} \tag{2.5.17}$$

для Рівняння до прямокутної гіперболи називають її асимптотами координатними осями. Геометрична інтерпретація$c$ показана на малюнку$\text{II.32}$, для якого намальовано$c = 1$, і ми назвали координатні$x$ осі і$y$. Довжина напівпоперечної осі дорівнює$c \sqrt{2}$.

$\text{FIGURE II.32}$

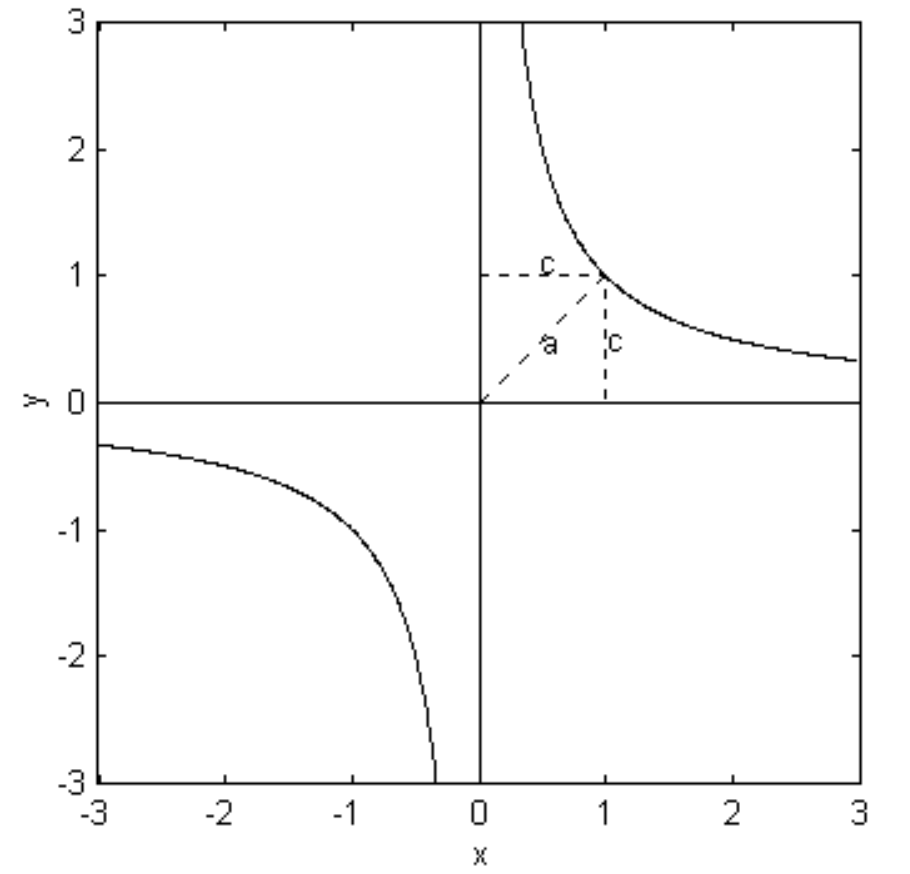
Просте рівняння$y = 1/x$ - це прямокутна гіпербола, і справді саме це рівняння показано на малюнку$\text{II.32}$.

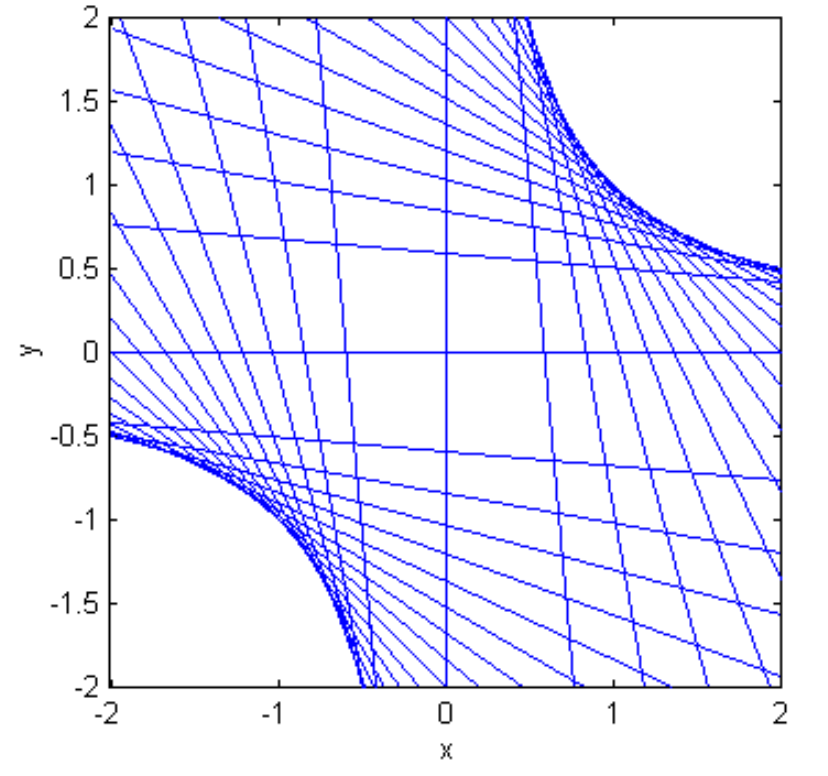
Залишено читачеві показати, що параметричні Рівняння прямокутної гіперболи$xy = c^2$ (ми скинули прості числа) є$x = ct, \ y = c/t$, що лінії форми$y=mx \pm 2c \sqrt{-m}$ дотичні до$xy = c^2$ (рис. II.35, намальовані з нахилами від$90^\circ$ до$180^\circ$ з кроком$5^\circ$), і що тангенс при$(x_1 , y_1 )$ є$x_1y + y_1x = 2c$.

$\text{FIGURE II.33}$

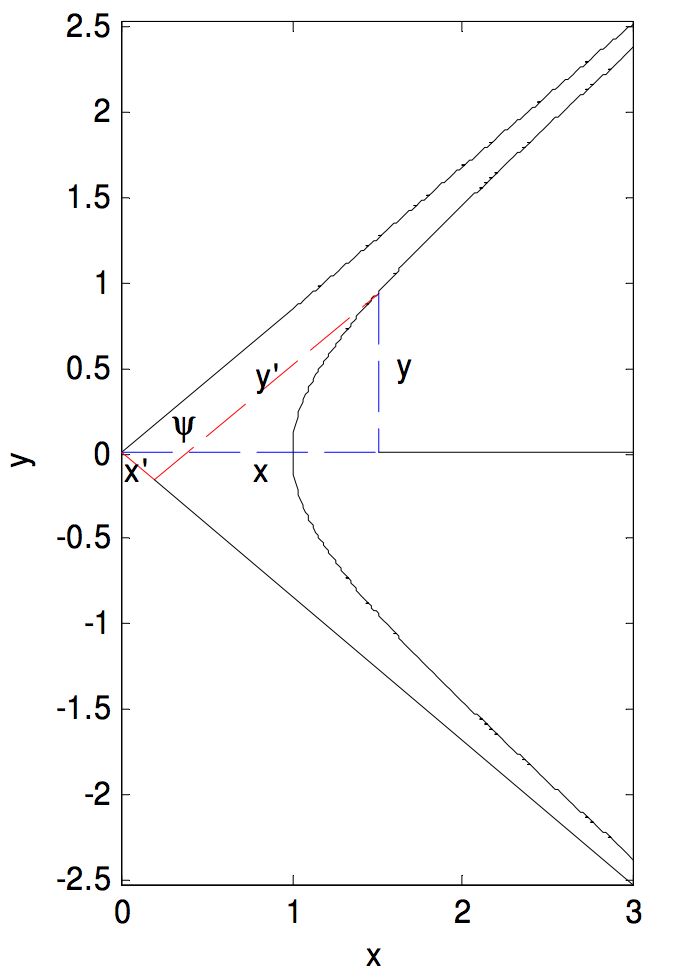
Рівняння гіперболи називають її асимптотами осями координат

Ми показали, що рівняння до прямокутної гіперболи називають її асимптотами як осі координат$x^\prime y^\prime = \frac{1}{2} a^2 = c^2$. Насправді рівняння$x^\prime y^\prime = c^2$ - це рівняння до будь-якої гіперболи (по центру$(0 ,\ 0)$), не обов'язково прямокутної, коли його називають асимптотами як осі координат, де$c^2 = \frac{1}{4} (a^2 + b^2)$ На малюнку нижче я намалював гіперболу і точку на гіперболі, координати якої щодо горизонтальна і вертикальна осі є$(x , \ y)$, і координати яких щодо асимптот є$(x^\prime , y^\prime)$. Я показав відстані$x$ і$y$ з синіми пунктирними лініями, і відстанями$x^\prime$ і$y^\prime$ з червоними пунктирними лініями. Напівкут між асимптотами дорівнює$ψ$.

Рівняння до гіперболи, що відноситься до горизонтальної і вертикальної осей, є

$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1. \label{2.5.18} \tag{2.5.18}$$

З креслення ми бачимо, що

$$x = (x^\prime + y^\prime) \cos ψ, \quad y = (y^\prime - x^\prime) \sin ψ. \label{2.5.19a,b} \tag{2.5.19a,b}$$

Якщо ми підставимо їх у рівняння$\ref{2.5.18}$, а також скористаємося відношенням$\tan ψ = b/a$ (Рівняння$\ref{2.5.10}$), ми дійдемо до Рівняння до гіперболи, яку називають асимптотами як осі координат:

$$x^\prime y^\prime = \frac{1}{4}(a^2 + b^2) = c^2 . \label{2.5.20} \tag{2.5.20}$$

Полярне рівняння до гіперболи

Ми знайшли полярні рівняння до еліпса та параболи по-різному. Тепер поверніться назад і подивіться на обидва методи і використовуйте будь-який (або обидва), щоб показати, що полярне рівняння до гіперболи (фокус як полюс) є

$$r = \frac{l}{1+ e \cos \theta}. \tag{2.5.21} \label{2.5.21}$$

Це полярне рівняння до будь-якого конічного перерізу - яке визначається виключно значенням$e$. Ви також повинні запитати себе, що представлено рівнянням

$$r = \frac{l}{1-e \cos \theta}. \label{2.5.22} \tag{2.5.22}$$

Спробуйте накидати його для різних значень$e$.