11.5: Конічні перерізи
- Page ID
- 61727
- Визначте рівняння параболи в стандартній формі з заданим фокусом і директрисою.
- Визначте рівняння еліпса в стандартній формі з заданими вогнищами.
- Визначте рівняння гіперболи в стандартній формі з заданими вогнищами.
- Розпізнайте параболу, еліпс або гіперболу за значенням її ексцентриситету.
- Запишіть полярне рівняння конічного перерізу з ексцентриситетом\(e\).
- Визначте, коли загальне рівняння другого ступеня є параболою, еліпсом або гіперболою.
Конічні розрізи вивчалися ще з часів стародавніх греків, і вважалися важливим математичним поняттям. Ще в 320 році до н.е. Такі грецькі математики, як Менаехм, Апполлоній, Архімед були зачаровані цими кривими. Апполлоній написав цілий восьмитомний трактат про конічних перерізах, в якому він, наприклад, зміг вивести специфічний метод ідентифікації конічного перерізу за допомогою використання геометрії. З тих пір виникли важливі застосування конічних перерізів (наприклад, в астрономії), а властивості конічних перерізів використовуються в радіотелескопах, приймачах супутникових антен і навіть в архітектурі. У цьому розділі ми обговоримо три основні конічні перерізи, деякі їх властивості та їх рівняння.
Конічні перерізи отримали свою назву тому, що вони можуть бути створені шляхом перетину площини з конусом. Конус має дві однакові за формою частини, які називаються ворсом. Одна підгузник - це те, що більшість людей мають на увазі під «конусом», маючи форму вечірнього капелюха. Правий круговий конус може бути сформований обертанням лінії, що проходить через початок навколо осі y, як показано на малюнку\(\PageIndex{1}\).
Конічні перерізи генеруються перетином площини з конусом (рис.\(\PageIndex{2}\)). Якщо площина паралельна осі обертання (осі y), то конічний перетин є гіперболою. Якщо площина паралельна формує лінії, то конічний переріз є параболою. Якщо площина перпендикулярна осі обертання, конічний перетин - це коло. Якщо площина перетинається одним ворсом під кутом до осі (відмінним
Параболи
Парабола генерується, коли площина перетинає конус, паралельний генеруючій лінії. При цьому площину перетинає тільки один з ворсинок. Параболу також можна визначити з точки зору відстаней.
Парабола - це сукупність всіх точок, відстань яких від нерухомої точки, званої фокусом, дорівнює відстані від нерухомої лінії, званої директрисою. Точка на півдорозі між фокусом і директрисою називається вершиною параболи.
Графік типової параболи відображається на малюнку\(\PageIndex{3}\). Використовуючи цю діаграму в поєднанні з формулою відстані, ми можемо вивести рівняння для параболи. Нагадаємо формулу відстані: Задана точка P з координатами\((x_1,y_1)\) і точка Q з координатами\((x_2,y_2),\) відстань між ними задається за формулою
\[d(P,Q)=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}. \nonumber \]
Тоді з визначення параболи і\(\PageIndex{3}\) малюнка отримаємо
\[d(F,P)=d(P,Q) \nonumber \]
\[\sqrt{(0−x)^2+(p−y)^2}=\sqrt{(x−x)^2+(−p−y)^2}. \nonumber \]
Квадратування обох сторін і спрощення врожайності
\[ \begin{align} x^2+(p−y)^2 = 0^2+(−p−y)^2 \\ x^2+p^2−2py+y^2 = p^2+2py+y^2 \\ x^2−2py =2py \\ x^2 =4py. \end{align} \nonumber \]
Тепер припустимо, ми хочемо, щоб перемістити вершину. Використовуємо змінні\((h,k)\) для позначення координат вершини. Тоді, якщо фокус знаходиться безпосередньо над вершиною, він має координати,\((h,k+p)\) а директриса має рівняння\(y=k−p\). Проходячи через ту ж деривацію, виходить формула\((x−h)^2=4p(y−k)\). Рішення цього рівняння для\(y\) призводить до наступної теореми.
З огляду на параболу, що відкривається вгору з вершиною, розташованою на,\((h,k)\) і фокусом\((h,k+p)\), розташованим на, де\(p\) є константа, рівняння для параболи задається
\[y=\dfrac{1}{4p}(x−h)^2+k. \nonumber \]
Це стандартна форма параболи.
Ми також можемо вивчити випадки, коли парабола відкривається вниз або вліво або вправо. Рівняння для кожного з цих випадків також може бути записано в стандартному вигляді, як показано на наступних графіках.
Крім того, рівняння параболи можна записати в загальному вигляді, хоча в такому вигляді значення\(h\)\(k\), і не відразу\(p\) впізнаються. Загальна форма параболи пишеться як
\[ax^2+bx+cy+d=0 \label{para1} \]
або
\[ay^2+bx+cy+d=0.\label{para2} \]
Рівняння\ ref {para1} являє собою параболу, яка відкривається або вгору, або вниз. Рівняння\ ref {para2} являє собою параболу, яка відкривається або ліворуч, або праворуч. Щоб поставити рівняння в стандартний вигляд, скористайтеся методом заповнення квадрата.
Ставимо рівняння
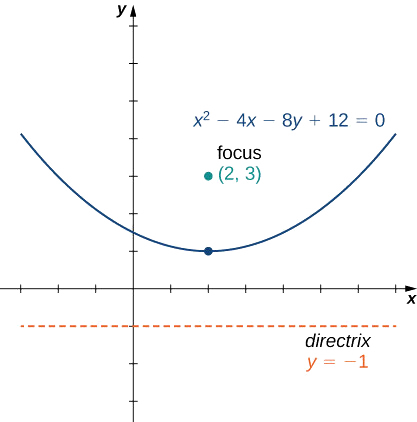
\[x^2−4x−8y+12=0 \nonumber \]
в стандартну форму і графувати отриману параболу.
Рішення
Оскільки y не знаходиться в квадраті в цьому рівнянні, ми знаємо, що парабола відкривається або вгору, або вниз. Тому нам потрібно вирішити це рівняння для y, яке поставить рівняння в стандартний вигляд. Для цього спочатку додайте\(8y\) до обох сторін рівняння:
\[8y=x^2−4x+12. \nonumber \]
Наступний крок - завершити квадрат з правого боку. Почніть з групування перших двох термінів праворуч за допомогою дужок:
\[8y=(x^2−4x)+12. \nonumber \]
Далі визначте константу, яка при додаванні всередині дужок робить величину всередині дужок ідеальним квадратним триноміалом. Для цього візьміть половину коефіцієнта х і квадрат його. Це дає\((\dfrac{−4}{2})^2=4.\) Додати 4 всередині дужок і відняти 4 поза дужками, тому значення рівняння не змінюється:
\[8y=(x^2−4x+4)+12−4. \nonumber \]
Тепер об'єднайте подібні терміни та коефіцієнт кількості всередині дужок:
\[8y=(x−2)^2+8. \nonumber \]
Нарешті, розділіть на 8:
\[y=\dfrac{1}{8}(x−2)^2+1. \nonumber \]
Це рівняння зараз знаходиться в стандартному вигляді. Порівняння цього з рівнянням дає\(h=2, k=1\), і\(p=2\). Парабола відкривається вгору, з вершиною на\((2,1)\), фокусом на\((2,3)\) та директрисі\(y=−1\). Графік цієї параболи виглядає наступним чином.
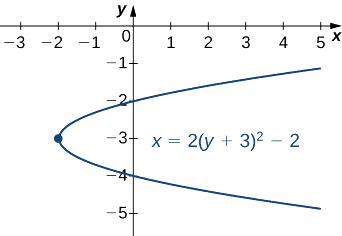
Помістіть рівняння\(2y^2−x+12y+16=0\) в стандартний вигляд і зробіть графік отриманої параболи.
- Підказка
-
Вирішити для\(x\). Перевірте, в якому напрямку відкривається парабола.
- Відповідь
-
\[x=2(y+3)^2−2 \nonumber \]
Вісь симетрії вертикальної (відкривається вгору або вниз) параболи являє собою вертикальну лінію, що проходить через вершину. Парабола має цікаве світловідбиваючу властивість. Припустимо, у нас є супутникова антена з параболічним перетином. Якщо пучок електромагнітних хвиль, таких як світло або радіохвилі, потрапляє в тарілку по прямій лінії від супутника (паралельно осі симетрії), то хвилі відбиваються від тарілки і збираються у фокусі параболи, як показано на малюнку.
Розглянемо параболічну тарілку, призначену для збору сигналів з супутника в космосі. Блюдо спрямоване безпосередньо на супутник, а у фокусі параболи розташований приймач. Радіохвилі, що надходять із супутника, відбиваються від поверхні параболи до приймача, який збирає та декодує цифрові сигнали. Це дозволяє невеликому приймачу збирати сигнали з широкого кута неба. Ліхтарі і фари в автомобілі працюють за тим же принципом, але в зворотному напрямку: джерело світла (тобто лампочка) розташовується в фокусі і відбиває поверхню на параболічному дзеркалі фокусує промінь прямо вперед. Це дозволяє невеликій лампочці висвітлювати широкий кут простору перед ліхтариком або автомобілем.
еліпси
Еліпс також можна визначити з точки зору відстаней. У випадку еліпса є два вогнища (множина фокусу) і дві директриси (множина директриси). Дивимося докладніше на директорії далі в цьому розділі.
Еліпс - це сукупність всіх точок, для яких сума їх відстаней від двох нерухомих точок (вогнищ) постійна.
Графік типового еліпса показаний на малюнку\(\PageIndex{6}\). На цьому малюнку вогнища\(F\) позначені як і\(F′\). Обидва є однаковою фіксованою відстанню від початку, і ця відстань представлена змінною\(c\). Тому координати\(F\) є\((c,0)\) і координати точки\(F′\)\(P\) і\(P′\) розташовані на кінцях великої осі еліпса, і мають координати\((a,0)\) і\((−a,0)\), відповідно.\((−c,0).\) Велика вісь завжди найдовша відстань через еліпс, і може бути горизонтальною або вертикальною. Таким чином, довжина великої осі в цьому еліпсі дорівнює\(2a\). Крім того,\(P\) і\(P′\) називаються вершинами еліпса. Точки\(Q\) і\(Q′\) розташовані на кінцях другорядної осі еліпса, і мають координати\((0,b)\) і\((0,−b),\) відповідно. Мала вісь - це найкоротша відстань через еліпс. Мала вісь перпендикулярна великій осі.
За визначенням еліпса ми можемо вибрати будь-яку точку на еліпсі і сума відстаней від цієї точки до двох вогнищ постійна. Припустимо, вибираємо точку\(P\). Так як координати точки\(P\) є\((a,0),\) сумою відстаней дорівнює
\[d(P,F)+d(P,F′)=(a−c)+(a+c)=2a. \nonumber \]
Тому сума відстаней від довільної точки А з координатами також\((x,y)\) дорівнює\(2a\). Використовуючи формулу відстані, отримуємо
\[d(A,F)+d(A,F′)=2a. \nonumber \]
\[\sqrt{(x−c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a \nonumber \]
Відніміть другий радикал з обох сторін і квадрат з обох сторін:
\[\sqrt{(x−c)^2+y^2}=2a−\sqrt{(x+c)^2+y^2} \nonumber \]
\[(x−c)^2+y^2=4a^2−4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \nonumber \]
\[x^2−2cx+c^2+y^2=4a^2−4a\sqrt{(x+c)^2+y^2}+x^2+2cx+c^2+y^2 \nonumber \]
\[−2cx=4a^2−4a\sqrt{(x+c)^2+y^2}+2cx. \nonumber \]
Тепер виділіть радикал з правого боку і знову квадрат:
\[−2cx=4a^2−4a\sqrt{(x+c)^2+y^2}+2cx \nonumber \]
\[4a\sqrt{(x+c)^2+y^2}=4a^2+4cx \nonumber \]
\[\sqrt{(x+c)^2+y^2}=a+\dfrac{cx}{a} \nonumber \]
\[(x+c)^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2} \nonumber \]
\[x^2+2cx+c^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2} \nonumber \]
\[x^2+c^2+y^2=a^2+\dfrac{c^2x^2}{a^2}. \nonumber \]
Виділіть змінні в лівій частині рівняння і константи з правого боку:
\[x^2−\dfrac{c^2x^2}{a^2}+y^2=a^2−c^2 \nonumber \]
\[\dfrac{(a^2−c^2)x^2}{a^2}+y^2=a^2−c^2. \nonumber \]
Розділіть обидві сторони на\(a^2−c^2\). Це дає рівняння
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2−c^2}=1. \nonumber \]
Якщо ми повернемося до малюнка\(\PageIndex{6}\), то довжина кожного з двох зелених відрізків лінії дорівнює\(a\). Це вірно тому, що сума відстаней від точки\(Q\) до вогнищ\(F′\) дорівнює\(F\) і дорівнює\(2a\), а довжини цих двох відрізків лінії рівні. Цей відрізок лінії утворює прямокутний трикутник з довжиною гіпотенузи\(a\) і довжинами катетів\(b\) і\(c\). З теореми Піфагора,\(b^2+c^2=a^2\) і\(b^2=a^2−c^2\). Тому рівняння еліпса стає
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1. \nonumber \]
Нарешті, якщо центр еліпса переміщений від початку до точки\((h,k)\), ми маємо наступну стандартну форму еліпса.
Розглянемо еліпс з центром\((h,k)\), горизонтальну велику вісь з довжиною\(2a\) і вертикальну незначну вісь з довжиною\(2b\). Тоді рівняння цього еліпса в стандартному вигляді
\[\dfrac{(x−h)^2}{a^2}+\dfrac{(y−k)^2}{b^2}=1 \label{HorEllipse} \]
а вогнища розташовуються при\((h±c,k)\), де\(c^2=a^2−b^2\). Рівняння напрямків є\(x=h±\dfrac{a^2}{c}\).
Якщо велика вісь вертикальна, то рівняння еліпса стає
\[\dfrac{(x−h)^2}{b^2}+\dfrac{(y−k)^2}{a^2}=1 \label{VertEllipse} \]
а вогнища розташовуються при\((h,k±c)\), де\(c^2=a^2−b^2\). Рівняння директрик в даному випадку є\(y=k±\dfrac{a^2}{c}\).
Якщо велика вісь горизонтальна, то еліпс називається горизонтальним, а якщо велика вісь вертикальна, то еліпс називається вертикальним. Рівняння еліпса в загальному вигляді, якщо воно в формі
\[Ax^2+By^2+Cx+Dy+E=0, \nonumber \]
де A і B є або позитивними, або обома негативними. Щоб перетворити рівняння із загальної форми в стандартну форму, скористайтеся методом заповнення квадрата.
Ставимо рівняння
\[9x^2+4y^2−36x+24y+36=0 \nonumber \]
в стандартну форму і графувати отриманий еліпс.
Рішення
Спочатку відніміть 36 з обох сторін рівняння:
\[9x^2+4y^2−36x+24y=−36. \nonumber \]
Далі згрупуйте\(x\) терміни разом і\(y\) терміни разом, і врахуйте загальний фактор:
\[(9x^2−36x)+(4y^2+24y)=−36 \nonumber \]
\[9(x^2−4x)+4(y^2+6y)=−36. \nonumber \]
Нам потрібно визначити константу, яка при додаванні всередині кожного набору дужок призводить до ідеального квадрата. У першому наборі дужок візьміть половину коефіцієнта x і квадрат його. Це дає\((\dfrac{−4}{2})^2=4.\) У другому наборі дужок взяти половину коефіцієнта y і квадрат його. Це дає\((\dfrac{6}{2})^2=9.\) Додати їх всередині кожної пари дужок. Оскільки перший набір дужок має 9 спереду, ми насправді додаємо 36 на лівій стороні. Аналогічно ми додаємо 36 до другого набору, а також. Тому рівняння стає
\[9(x^2−4x+4)+4(y^2+6y+9)=−36+36+36 \nonumber \]
\[9(x^2−4x+4)+4(y^2+6y+9)=36. \nonumber \]
Тепер множник обох наборів дужок і ділимо на 36:
\[9(x−2)^2+4(y+3)^2=36 \nonumber \]
\[\dfrac{9(x−2)^2}{36}+\dfrac{4(y+3)^2}{36}=1 \nonumber \]
\[\dfrac{(x−2)^2}{4}+\dfrac{(y+3)^2}{9}=1. \nonumber \]
Рівняння тепер в стандартній формі. Порівняння цього з рівнянням\ ref {Vertellipse} дає\(h=2, k=−3, a=3,\) і\(b=2\). Це вертикальний еліпс з центром в\((2,−3)\), великою віссю 6 і малою віссю 4. Графік цього еліпса виглядає наступним чином.

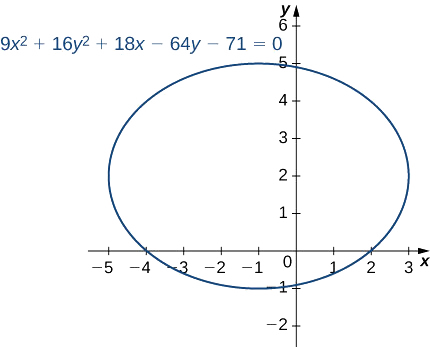
Ставимо рівняння
\[9x^2+16y^2+18x−64y−71=0 \nonumber \]
в стандартну форму і графувати отриманий еліпс.
- Підказка
-
Перемістіть константу над і завершіть квадрат.
- Відповідь
-
\[\dfrac{(x+1)^2}{16}+\dfrac{(y−2)^2}{9}=1 \nonumber \]
Згідно з першим законом Кеплера про рух планет, орбіта планети навколо Сонця являє собою еліпс з Сонцем в одному з вогнищ, як показано на малюнку\(\PageIndex{8A}\). Оскільки орбіта Землі є еліпсом, відстань від Сонця змінюється протягом року. Поширеною помилкою є те, що Земля ближче до Сонця влітку. Насправді влітку для північної півкулі Земля знаходиться далі від Сонця, ніж взимку. Різниця в сезоні обумовлена нахилом осі Землі в орбітальній площині. Комети, які обертаються навколо Сонця, такі як комета Галлея, також мають еліптичні орбіти, як і супутники, що обертаються навколо планет і супутників, що обертаються навколо Землі.
Еліпси також мають цікаві світловідбиваючі властивості: світловий промінь, що виходить від одного фокусу, проходить через інший фокус після дзеркального відображення в еліпсі. Те ж саме відбувається і зі звуковою хвилею. Національний скульптурний зал в Капітолії США у Вашингтоні, округ Колумбія, є відомою кімнатою в еліптичній формі, як показано на малюнку\(\PageIndex{8B}\). Цей зал служив місцем зустрічі Палати представників США майже п'ятдесят років. Розташування двох вогнищ цієї напівеліптичної кімнати чітко позначено відмітками на підлозі, і навіть якщо кімната переповнена відвідувачами, коли двоє людей стоять на цих плямах і розмовляють один з одним, вони можуть чути один одного набагато чіткіше, ніж чути когось, хто стоїть поруч. Легенда свідчить, що Джон Квінсі Адамс мав свій стіл, розташований на одному з вогнищ і зміг підслуховувати всіх інших у Будинку, не потребуючи стояти. Хоча це і робить хорошу історію, навряд чи це буде правдою, адже оригінальна стеля видав стільки відгомонів, що всю кімнату довелося повісити килимами, щоб гасити шум. Стеля був відбудований у 1902 році, і лише тоді з'явився відомий зараз ефект шепоту. Ще одна відома шепітна галерея - місце багатьох пропозицій про шлюб - знаходиться на Центральному вокзалі в Нью-Йорку.
Гіперболи
Гіпербола також може бути визначена з точки зору відстаней. У разі гіперболи виділяють два вогнища і дві спрямованості. Гіперболи також мають два асимптоти.
Гіпербола - це сукупність всіх точок, де різниця між їх відстанями від двох нерухомих точок (вогнищ) постійна.
Графік типової гіперболи з'являється наступним чином.
Виведення рівняння гіперболи в стандартній формі практично ідентично рівнянню еліпса. Одна невелика заковика полягає у визначенні: різниця між двома числами завжди позитивна. \(P\)Дозволяти точка на гіперболі з координатами\((x,y)\). Потім дає визначення гіперболи\(|d(P,F_1)−d(P,F_2)|=constant\). Щоб спростити виведення, припустимо, що\(P\) знаходиться на правій гілці гіперболи, тому стовпчики абсолютного значення падають. Якщо він знаходиться на лівій гілці, то віднімання відбувається зворотним. Вершина правої гілки має координати\((a,0),\) так
\[d(P,F_1)−d(P,F_2)=(c+a)−(c−a)=2a. \nonumber \]
Тому це рівняння вірно для будь-якої точки гіперболи. Повернення до координат\((x,y)\) для\(P\):
\[d(P,F_1)−d(P,F_2)=2a \nonumber \]
\[\sqrt{(x+c)^2+y^2}−\sqrt{(x−c)^2+y^2}=2a. \nonumber \]
Виділяють другий радикал і квадрат з обох сторін:
\[\sqrt{(x−c)^2+y^2}=-2a+\sqrt{(x+c)^2+y^2} \nonumber \]
\[(x−c)^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 \nonumber \]
\[x^2−2cx+c^2+y^2=4a^2-4a\sqrt{(x+c)^2+y^2}+x^2+2cx+c^2+y^2 \nonumber \]
\[−2cx=4a^2-4a\sqrt{(x+c)^2+y^2}+2cx. \nonumber \]
Тепер виділіть радикал з правого боку і знову квадрат:
\(−2cx=4a^2-4a\sqrt{(x+c)^2+y^2}+2cx\)
\(-4a\sqrt{(x+c)^2+y^2}=−4a^2−4cx\)
\(-\sqrt{(x+c)^2+y^2}=−a−\dfrac{cx}{a}\)
\((x+c)^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2}\)
\(x^2+2cx+c^2+y^2=a^2+2cx+\dfrac{c^2x^2}{a^2}\)
\(x^2+c^2+y^2=a^2+\dfrac{c^2x^2}{a^2}\).
Виділіть змінні в лівій частині рівняння і константи з правого боку:
\[x^2−\dfrac{c^2x^2}{a^2}+y^2=a^2−c^2 \nonumber \]
\[\dfrac{(a^2−c^2)x^2}{a^2}+y^2=a^2−c^2. \nonumber \]
Нарешті, розділіть обидві сторони на\(a^2−c^2\). Це дає рівняння
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2−c^2}=1. \nonumber \]
Тепер ми визначаємо б так, що\(b^2=c^2−a^2\). Це можливо тому, що\(c>a\). Тому рівняння гіперболи стає
\[\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1. \nonumber \]
Нарешті, якщо центр гіперболи переміщений від початку до точки,\((h,k),\) ми маємо наступну стандартну форму гіперболи.
Розглянемо гіперболу з центром\((h,k)\), горизонтальною великою віссю та вертикальною незначною віссю. Тоді рівняння цієї гіперболи
\[\dfrac{(x−h)^2}{a^2}−\dfrac{(y−k)^2}{b^2}=1 \label{HorHyperbola} \]
а вогнища розташовуються\((h±c,k),\) там де\(c^2=a^2+b^2\). Рівняння асимптотів\(y=k±\dfrac{b}{a}(x−h).\) задаються рівняннями директрик
\[x=h±\dfrac{a^2}{\sqrt{a^2+b^2}}=h±\dfrac{a^2}{c} \nonumber \]
Якщо велика вісь вертикальна, то рівняння гіперболи стає
\[\dfrac{(y−k)^2}{a^2}−\dfrac{(x−h)^2}{b^2}=1 \nonumber \]
а вогнища розташовуються\((h,k±c),\) там де\(c^2=a^2+b^2\). Рівняння асимптотів задаються за допомогою\(y=k±\dfrac{a}{b}(x−h)\). Рівняння директрис є
\[y=k±\dfrac{a^2}{\sqrt{a^2+b^2}}=k±\dfrac{a^2}{c}. \nonumber \]
Якщо велика вісь (поперечна вісь) горизонтальна, то гіперболу називають горизонтальною, а якщо велика вісь вертикальна, то гіперболу називають вертикальною. Рівняння гіперболи знаходиться в загальному вигляді, якщо воно в формі
\[Ax^2+By^2+Cx+Dy+E=0, \nonumber \]
де А і В мають протилежні знаки. Для того щоб перетворити рівняння з загальної в стандартну форму, скористайтеся методом заповнення квадрата.
Помістіть рівняння\(9x^2−16y^2+36x+32y−124=0\) в стандартну форму і зробіть графік отриманої гіперболи. Які існують рівняння асимптотів?
Рішення
Спочатку додайте 124 до обох сторін рівняння:
\(9x^2−16y^2+36x+32y=124.\)
Далі згрупуйте терміни x разом та терміни y разом, а потім врахуйте загальні фактори:
\((9x^2+36x)−(16y^2−32y)=124\)
\(9(x^2+4x)−16(y^2−2y)=124\).
Нам потрібно визначити константу, яка при додаванні всередині кожного набору дужок призводить до ідеального квадрата. У першому наборі дужок візьміть половину коефіцієнта x і квадрат його. Це дає\((\dfrac{4}{2})^2=4\). У другому наборі дужок візьміть половину коефіцієнта y і квадрат його. Це дає\((\dfrac{−2}{2})^2=1.\) Додати їх всередині кожної пари дужок. Оскільки перший набір дужок має 9 спереду, ми насправді додаємо 36 на лівій стороні. Аналогічно ми віднімаємо 16 з другого набору дужок. Тому рівняння стає
\(9(x^2+4x+4)−16(y^2−2y+1)=124+36−16\)
\(9(x^2+4x+4)−16(y^2−2y+1)=144.\)
Наступний множник обидві множини дужок і ділять на 144:
\(9(x+2)^2−16(y−1)^2=144\)
\(\dfrac{9(x+2)^2}{144}−\dfrac{16(y−1)^2}{144}=1\)
\(\dfrac{(x+2)^2}{16}−\dfrac{(y−1)^2}{9}=1.\)
Рівняння тепер в стандартній формі. Порівняння цього з рівнянням\ ref {HorHyperbola} дає\(h=−2, k=1, a=4,\) і\(b=3\). Це горизонтальна гіпербола з центром в\((−2,1)\) і асимптотами, заданими рівняннями\(y=1±\dfrac{3}{4}(x+2)\). Графік цієї гіперболи відображається на рис\(\PageIndex{10}\).
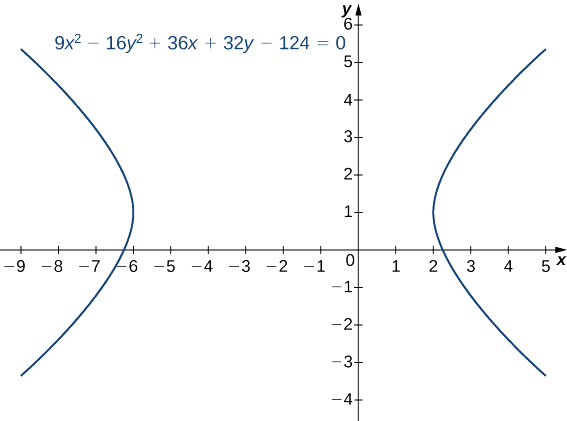
Помістіть рівняння\(4y^2−9x^2+16y+18x−29=0\) в стандартну форму і зробіть графік отриманої гіперболи. Які існують рівняння асимптотів?
- Підказка
-
Перемістіть константу над і завершіть квадрат. Перевірте, в якому напрямку відкривається гіпербола
- Відповідь
-
\(\dfrac{(y+2)^2}{9}−\dfrac{(x−1)^2}{4}=1.\)Це вертикальна гіпербола. Асимптоти\(y=−2±\dfrac{3}{2}(x−1).\)

Гіперболи також мають цікаві світловідбиваючі властивості. Промінь, спрямований до одного вогнища гіперболи, відбивається гіперболічним дзеркалом до іншого вогнища. Це поняття проілюстровано на рис\(\PageIndex{11}\).
Це властивість гіперболи має важливі застосування. Застосовується в радіопеленгації (так як різниця сигналів від двох веж постійна уздовж гіпербол), і в конструкції дзеркал всередині телескопів (для відображення світла, що надходить від параболічного дзеркала до окуляра). Ще один цікавий факт про гіперболи полягає в тому, що для комети, що входить в Сонячну систему, якщо швидкість досить велика, щоб уникнути гравітаційного потягу Сонця, то шлях, який проходить комета, проходячи через Сонячну систему, є гіперболічним.
Ексцентриситет і Directrix
Альтернативний спосіб опису конічного перерізу включає напрямки, вогнища та нову властивість, яка називається ексцентриситетом. Ми побачимо, що значення ексцентриситету конічного перерізу може однозначно визначити цей конічний.
Ексцентриситет \(e\)конічного перерізу визначається як відстань від будь-якої точки конічного перерізу до його вогнища, поділена на перпендикулярну відстань від цієї точки до найближчої директриси. Це значення є постійним для будь-якого конічного перерізу і може визначати також конічний переріз:
- Якщо\(e=1\), конічний - парабола.
- Якщо\(e<1\), то це еліпс.
- Якщо\(e>1,\) це гіпербола.
Ексцентриситет кола дорівнює нулю. Директриса конічного перерізу - це лінія, яка разом з точкою, відомою як фокус, служить для визначення конічного перерізу. Гіперболи і некругові еліпси мають два вогнища і дві пов'язані з ними напрямки. Параболи мають один фокус і одну директрису.
Три конічних перерізу з їх напрямками зображені на рис\(\PageIndex{12}\).
Нагадаємо з визначення параболи, що відстань від будь-якої точки параболи до вогнища дорівнює відстані від тієї ж точки до директриси. Тому за визначенням ексцентриситет параболи повинен бути 1. Рівняння напрямків горизонтального еліпса є\(x=±\dfrac{a^2}{c}\). Права вершина еліпса розташована на,\((a,0)\) а правий фокус -\((c,0)\). Тому відстань від вершини до фокуса є,\(a−c\) а відстань від вершини до правої директриси є\(\dfrac{a^2}{c}−c.\) Це дає ексцентриситет як
\[e=\dfrac{a−c}{\dfrac{a^2}{c}−a}=\dfrac{c(a−c)}{a^2−ac}=\dfrac{c(a−c)}{a(a−c)}=\dfrac{c}{a}. \nonumber \]
Так як\(c<a\) цей крок доводить, що ексцентриситет еліпса менше 1. Напрямки горизонтальної гіперболи також розташовані на\(x=±\dfrac{a^2}{c}\), і подібний розрахунок показує, що ексцентриситет гіперболи також є\(e=\dfrac{c}{a}\). Однак у цьому випадку ми маємо\(c>a\), тому ексцентриситет гіперболи більше 1.
Визначте ексцентриситет еліпса, описаного рівнянням
\(\dfrac{(x−3)^2}{16}+\dfrac{(y+2)^2}{25}=1.\)
Рішення
З рівняння бачимо, що\(a=5\) і\(b=4\). Значення c можна обчислити за допомогою рівняння\(a^2=b^2+c^2\) для еліпса. Підстановка значень a і b і розв'язування для c дає\(c=3\). Тому ексцентриситет еліпса дорівнює\(e=\dfrac{c}{a}=\dfrac{3}{5}=0.6.\)
Визначте ексцентриситет гіперболи, описаної рівнянням
\(\dfrac{(y−3)^2}{49}−\dfrac{(x+2)^2}{25}=1.\)
- Підказка
-
Спочатку знайдіть значення a і b, потім визначте c за допомогою рівняння\(c^2=a^2+b^2\).
- Відповідь
-
\(e=\dfrac{c}{a}=\dfrac{\sqrt{74}}{7}≈1.229\)
Полярні рівняння конічних перерізів
Іноді корисно написати або ідентифікувати рівняння конічного перерізу в полярному вигляді. Для цього нам знадобиться поняття фокального параметра. Фокусний параметр конічного перерізу p визначається як відстань від фокуса до найближчої директриси. У наступній таблиці наведено фокусні параметри для різних типів коніків, де a - довжина напіввеликої осі (тобто половина довжини великої осі), c - відстань від початку до фокусу, а e - ексцентриситет. У випадку з параболою a представляє відстань від вершини до фокусу.
| Конічна | \(e\) | \(p\) |
|---|---|---|
| Еліпс | \ (e\)» style="вертикальне вирівнювання: середина; ">\(0<e<1\) | \ (p\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{a^2−c^2}{c}=\dfrac{a(1−e^2)}{c}\) |
| Парабола | \ (e\)» style="вертикальне вирівнювання: середина; ">\(e=1\) | \ (p\)» style="вертикальне вирівнювання: середина; ">\(2a\) |
| Гіпербола | \ (e\)» style="вертикальне вирівнювання: середина; ">\(e>1\) | \ (p\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{c^2−a^2}{c}=\dfrac{a(e^2−1)}{c}\) |
Використовуючи визначення фокального параметра та ексцентриситету конічного перерізу, можна вивести рівняння для будь-якого конічного перерізу в полярних координатах. Зокрема, припустимо, що один з вогнищ заданого конічного перерізу лежить на полюсі. Тоді за допомогою визначення різних конічних перерізів за відстанями можна довести наступну теорему.
Полярне рівняння конічного перерізу з фокусним параметром p задається
\(r=\dfrac{ep}{1±e\cos θ}\)або\(r=\dfrac{ep}{1±e\sin θ}.\)
У рівнянні зліва велика вісь конічного перерізу горизонтальна, а в рівнянні праворуч велика вісь вертикальна. Для роботи з конічним перерізом, записаним у полярній формі, спочатку зробіть постійний член в знаменнику рівним 1. Це можна зробити, розділивши і чисельник, і знаменник дробу на константу, яка з'являється перед плюсом або мінусом в знаменнику. Тоді коефіцієнт синуса або косинуса в знаменнику - ексцентриситет. Це значення ідентифікує конічний конус. Якщо в знаменнику з'являється косинус, то конічний - горизонтальний. Якщо з'являється синус, то конус вертикальний. Якщо обидва з'являються, то осі повертаються. Центр конічного конуса не обов'язково знаходиться біля початку. Центр знаходиться в початковій точці, тільки якщо конічним є коло (тобто\(e=0\)).
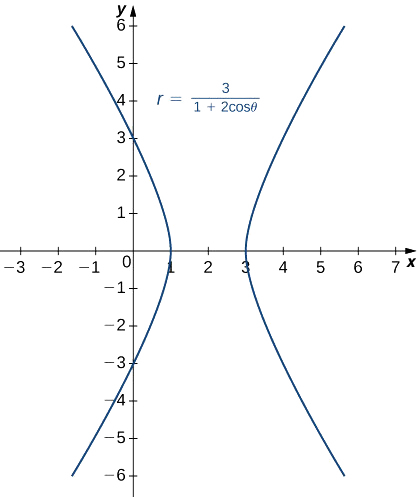
Визначте та створіть графік конічного перерізу, описаного рівнянням
\(r=\dfrac{3}{1+2\cos θ}\).
Рішення
Постійний член в знаменнику дорівнює 1, тому ексцентриситет конічного конуса дорівнює 2. Це гіпербола. Фокусний параметр p можна обчислити за допомогою рівняння\(ep=3.\) Since\(e=2\), це дає\(p=\dfrac{3}{2}\). Функція косинуса з'являється в знаменнику, тому гіпербола горизонтальна. Виберіть кілька значень для\(θ\) і створіть таблицю значень. Тоді ми можемо скласти графік гіперболи (рис.\(\PageIndex{13}\)).
| \(θ\) | \(r\) | \(θ\) | \(r\) |
|---|---|---|---|
| \ (θ\)» style="вертикальне вирівнювання: середина; "> 0 | \ (r\)» style="вертикальне вирівнювання: середина; "> 1 | \ (θ\)» style="вертикальне вирівнювання: середина; ">\(π\) | \ (r\)» style="вертикальне вирівнювання: середина; ">−3 |
| \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{π}{4}\) | \ (r\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{3}{1+\sqrt{2}}≈1.2426\) | \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{5π}{4}\) | \ (r\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{3}{1−\sqrt{2}}≈−7.2426\) |
| \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{π}{2}\) | \ (r\)» style="вертикальне вирівнювання: середина; "> 3 | \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{3π}{2}\) | \ (r\)» style="вертикальне вирівнювання: середина; "> 3 |
| \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{3π}{4}\) | \ (r\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{3}{1−\sqrt{2}}≈−7.2426\) | \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{7π}{4}\) | \ (r\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{3}{1+\sqrt{2}}≈1.2426\) |
Визначте та створіть графік конічного перерізу, описаного рівнянням
\(r=\dfrac{4}{1−0.8 \sin θ}\).
- Підказка
-
Спочатку знайдіть значення e і p, а потім створіть таблицю значень.
- Відповідь
-
Ось\(e=0.8\) і\(p=5\). Цей конічний переріз є еліпсом.
Загальні рівняння другого ступеня
Загальне рівняння ступеня два можна записати у вигляді
\[ Ax^2+Bxy+Cy^2+Dx+Ey+F=0. \nonumber \]
Графік рівняння такого виду є конічним перерізом. Якщо\(B≠0\) тоді осі координат обертаються. Для ідентифікації конічного перерізу використовується дискримінант конічного перерізу\(4AC−B^2.\)
Один з наступних випадків повинен бути вірним:
- \(4AC−B^2>0\). Якщо так, то граф є еліпсом.
- \(4AC−B^2=0\). Якщо так, то граф є параболою.
- \(4AC−B^2<0\). Якщо так, то графік є гіперболою.
Найпростішим прикладом рівняння другого ступеня, що включає перехресний член, є\(xy=1\). Це рівняння можна вирішити\(y\) для отримання\(y=\dfrac{1}{x}\). Графік цієї функції називається прямокутною гіперболою, як показано на малюнку.
Асимптотами цієї гіперболи є\(x\) осі\(y\) координат і. Для визначення кута θ повороту конічного перерізу скористаємося формулою\(\cot 2θ=\frac{A−C}{B}\). В даному випадку\(A=C=0\) і\(B=1\), так\(\cot 2θ=(0−0)/1=0\) і\(θ=45°\). Спосіб побудови графіка конічного перерізу з обертованими осями включає визначення коефіцієнтів конічного перерізу в оберненій системі координат. Нові коефіцієнти маркуються\(A′,B′,C′,D′,E′,\)\(F′,\) і задаються формулами
\[ \begin{align} A′ =A\cos^ 2θ+B\cos θ\sin θ+C\sin^2 θ \\ B′ =0 \\ C′ =A\sin^2 θ−B\sin θ\cos θ+C\cos^2θ \\ D′ =D\cos θ+E\sin θ \\ E′ =−D\sin θ+E\cosθ \\ F′ =F. \end{align} \nonumber \]
Порядок побудови графіка повернутого конічного конуса полягає в наступному:
- Визначте конічний переріз за допомогою дискримінанту\(4AC−B^2\).
- \(θ\)Визначаємося за допомогою формули\[\cot2θ=\dfrac{A−C}{B} \label{rot}. \]
- Розрахувати\(A′,B′,C′,D′,E′\), і\(F′\).
- Перепишіть вихідне рівняння за допомогою\(A′,B′,C′,D′,E′\), і\(F′\).
- Намалюйте графік, використовуючи повернуте рівняння.
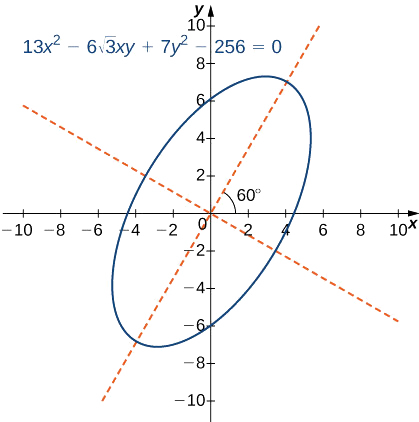
Визначити конічний і обчислити кут повороту осей для кривої, описаної рівнянням
\[13x^2−6\sqrt{3}xy+7y^2−256=0. \nonumber \]
Рішення
У цьому рівнянні\(A=13,B=−6\sqrt{3},C=7,D=0,E=0,\) і\(F=−256\). Дискримінант цього рівняння
\[4AC−B^2=4(13)(7)−(−6\sqrt{3})^2=364−108=256. \nonumber \]
Тому ця коніка є еліпсом.
Для обчислення кута повороту осей використовують Equation\ ref {rot}
\[\cot 2θ=\dfrac{A−C}{B}. \nonumber \]
Це дає
\(\cot 2θ=\dfrac{A−C}{B}=\dfrac{13−7}{−6\sqrt{3}}=−\dfrac{\sqrt{3}}{3}\).
Тому\(2θ=120^o\) і\(θ=60^o\), який кут повороту осей.
Для визначення обертових коефіцієнтів скористайтеся формулами, наведеними вище:
\(A′=A\cos^2θ+B\cos θ\sinθ+C\sin^2θ\)
\(=13\cos^260+(−6\sqrt{3})\cos 60 \sin 60+7\sin^260\)
\(=13(\dfrac{1}{2})^2−6\sqrt{3}(\dfrac{1}{2})(\dfrac{\sqrt{3}}{2})+7(\dfrac{\sqrt{3}}{2})^2\)
\(=4,\)
\(B′=0\)
\(C′=A\sin^2θ−B\sin θ\cos θ+C\cos^2θ\)
\(=13\sin^260+(6\sqrt{3})\sin 60 \cos 60+7\cos^260\)
\(=13(\dfrac{\sqrt{3}}{2})^2+6\sqrt{3}(\dfrac{\sqrt{3}}{2})(\dfrac{1}{2})+7(\dfrac{1}{2})^2\)
\(=16,\)
\(D′=D\cos θ+E\sin θ\)
\(=(0)\cos 60+(0)\sin 60\)
\(=0,\)
\(E′=−D\sin θ+E\cos θ\)
\(=−(0)\sin 60+(0)\cos 60\)
\(=0\)
\(F′= F\)
\(=−256.\)
Рівняння конічного конуса в оберненій системі координат стає
\(4(x′)^2+16(y′)^2=256\)
\(\dfrac{(x′)^2}{64}+\dfrac{(y′)^2}{16}=1\).
Графік цього конічного перерізу виглядає наступним чином.
Визначити конічний і обчислити кут повороту осей для кривої, описаної рівнянням
\[3x^2+5xy−2y^2−125=0. \nonumber \]
- Підказка
-
Виконайте кроки 1 і 2 п'ятикрокового методу, описаного вище
- Відповідь
-
Конічна - це гіпербола, а кут повороту осей дорівнює\(θ=22.5°.\)
Ключові поняття
- Рівняння вертикальної параболи в стандартній формі з заданим фокусом і директрисою\(p\) - це\(y=\dfrac{1}{4p}(x−h)^2+k\) де відстань від вершини до вогнища і\((h,k)\) є координатами вершини.
- Рівняння горизонтального еліпса в стандартній формі - це те,\(\dfrac{(x−h)^2}{a^2}+\dfrac{(y−k)^2}{b^2}=1\) де центр має координати\((h,k)\), велика вісь має довжину 2а, незначна вісь має довжину 2b, а координати\((h±c,k)\) вогнищ - де\(c^2=a^2−b^2\).
- Рівняння горизонтальної гіперболи в стандартній формі - це те\((h,k)\),\(\dfrac{(x−h)^2}{a^2}−\dfrac{(y−k)^2}{b^2}=1\) де центр має координати, вершини розташовані в\((h±a,k)\), а координати вогнищ -\((h±c,k),\) де\(c^2=a^2+b^2\).
- Ексцентриситет еліпса менше 1, ексцентриситет параболи дорівнює 1, а ексцентриситет гіперболи більше 1. Ексцентриситет кола дорівнює 0.
- Полярне рівняння конічного перерізу з ексцентриситетом e дорівнює\(r=\dfrac{ep}{1±ecosθ}\) або\(r=\dfrac{ep}{1±esinθ}\), де p представляє фокальний параметр.
- Для ідентифікації конічного конуса, породженого рівнянням\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\), спочатку обчислити дискримінант\(D=4AC−B^2\). Якщо\(D>0\) тоді конічний - еліпс, якщо\(D=0\) тоді конічний - парабола, а якщо\(D<0\) то конічний - гіпербола.
Глосарій
- конічний перетин
- конічний переріз - це будь-яка крива, утворена перетином площини з конусом двох ворсів
- директриса
- директриса (множина: директриси) — лінія, яка використовується для побудови та визначення конічного перерізу; парабола має одну директрису; еліпси та гіперболи мають два
- дискримінантний
- значення\(4AC−B^2\), яке використовується для ідентифікації конічного, коли рівняння містить член за участю\(xy\), називається дискримінантним
- фокус
- фокус (множина: вогнища) - точка, яка використовується для побудови та визначення конічного перерізу; парабола має один фокус; еліпс та гіпербола мають два
- ексцентриситет
- ексцентриситет визначається як відстань від будь-якої точки конічного перерізу до її фокусу, поділене на перпендикулярну відстань від цієї точки до найближчої директриси
- фокусний параметр
- фокальний параметр - відстань від фокуса конічного перерізу до найближчої директриси
- загальна форма
- рівняння конічного перерізу, записане як загальне рівняння другого ступеня
- велика вісь
- велика вісь конічного перерізу проходить через вершину у випадку параболи або через дві вершини у випадку еліпса або гіперболи; вона також є віссю симетрії конічного; також називається поперечною віссю
- незначна вісь
- незначна вісь перпендикулярна великій осі і перетинає велику вісь в центрі конічної, або у вершині у випадку параболи; також називається сполученою віссю
- дрімати
- підгузник - одна половина подвійного конуса
- стандартна форма
- рівняння конічного перерізу, показуючи його властивості, такі як розташування вершини або довжини великих і другорядних осей
- вершина
- вершина — крайня точка конічного перерізу; парабола має одну вершину в точці повороту. Еліпс має дві вершини, по одній на кожному кінці великої осі; гіпербола має дві вершини, по одній у точці повороту кожної гілки
