3.E: Інтеграл (вправи)
- Page ID
- 60274
3.1 Вправи
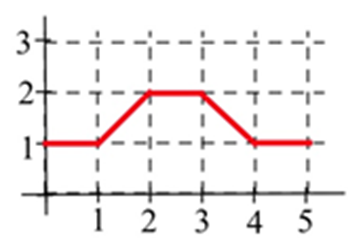
\(A(x)\)Дозволяти представляти область, обмежену графіком і горизонтальною віссю і вертикальними лініями на\(t=0\) і\(t=x\) для показаного графіка. Оцініть\(A(x)\) для\(x =\) 1, 2, 3, 4 і 5.
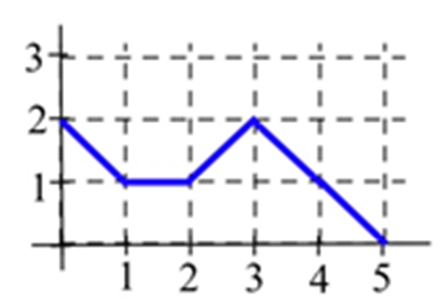
\(B(x)\)Дозволяти представляти область, обмежену графіком і горизонтальною віссю і вертикальними лініями на\(t=0\) і\(t=x\) для показаного графіка. Оцініть\(B(x)\) для\(x =\) 1, 2, 3, 4 і 5.
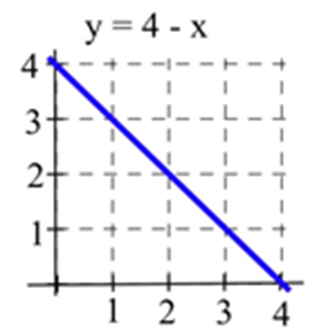
\(C(x)\)Дозволяти представляти область, обмежену графіком і горизонтальною віссю і вертикальними лініями на\(t=0\) і\(t=x\) для показаного графіка. Оцініть\(C(x)\) для\(x =\) 1, 2 і 3 і знайдіть формулу для\(C(x)\).
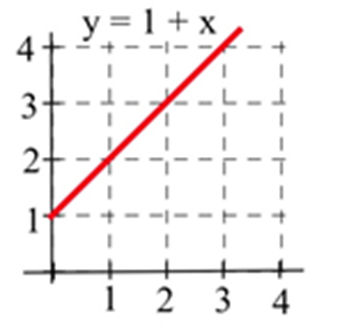
\(A(x)\)Дозволяти представляти область, обмежену графіком і горизонтальною віссю і вертикальними лініями на\(t=0\) і\(t=x\) для показаного графіка. Оцініть\(A(x)\) для\(x =\) 1, 2 і 3 і знайдіть формулу для\(A(x)\).
Автомобіль мав швидкість, показану на графіку праворуч.
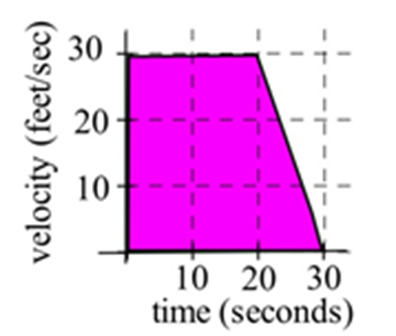
Автомобіль мав швидкість, показану на графіку праворуч. Як далеко проїхала машина від\(t= 0\) до\(t = 30\) секунди?
Автомобіль мав швидкість, показану нижче.
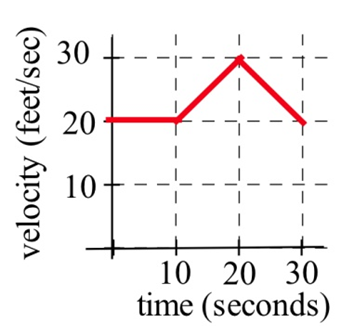
Як далеко автомобіль проїхав від\(t = 0\) до\(t = 30\) секунд?
Швидкості двох автомобілів наведені на графіку.
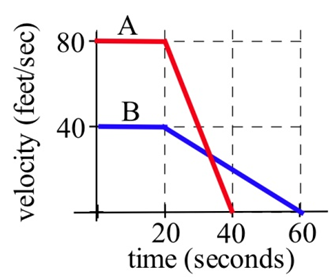
(а) З моменту застосування гальм, скільки секунд знаходилося кожному автомобілю, щоб зупинитися?
(б) З моменту застосування гальм, який автомобіль їхав далі, поки не дійшов до повної зупинки?
Ви з другом починаєте опівдні і йдете в тому ж напрямку по тому ж шляху за показаними ставками.
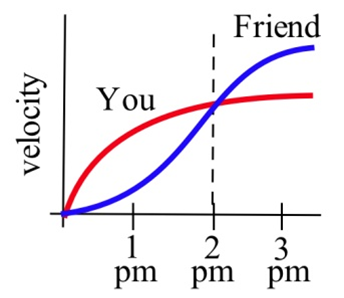
(а) Хто швидше ходить о 14:00? Хто попереду о 2 годині вечора?
(б) Хто швидше ходить о 3 годині вечора? Хто попереду о 3 годині вечора?
(c) Коли ви і ваш друг будете разом? (Відповідь словами.)
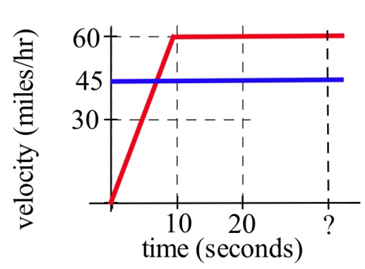
Поліцейська погоня: Швидкіс, який подорожує 45 миль на годину (у зоні 25 миль/год), проходить зупинену поліцейську машину, яка негайно злітає після швидкості. Якщо поліцейська машина стабільно прискорюється до 60 миль/год за 20 секунд, а потім їде зі стійким 60 миль/год, як довго і як далеко до того, як поліцейська машина зловить швидкісного, який продовжував подорожувати зі швидкістю 45 миль/год?
Вода стікає в ванну. У таблиці вказана швидкість, з якою протікає вода, в галонах/хвилину. Ванна спочатку порожня.
|
\(t\), за лічені хвилини |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Швидкість потоку, в галлонів/хв |
0.5 |
1.0 |
1.2 |
1.4 |
1.7 |
2.0 |
2.3 |
1.8 |
0.7 |
0.5 |
0.2 |
Скористайтеся таблицею, щоб оцінити, скільки води знаходиться у ванні після
a. п'ять хвилин
б. десять хвилин
У таблиці наведені показання спідометра за коротку поїздку на автомобілі.
|
\(t\), за лічені хвилини |
0 |
5 |
10 |
15 |
20 |
|
Швидкість руху, в миль/год |
0 |
30 |
40 |
65 |
40 |
a Використовуйте таблицю, щоб оцінити, наскільки далеко автомобіль проїхав протягом двадцяти хвилин, показаних.
б Наскільки точною ви очікуєте, що ваша оцінка буде?
У таблиці наведені значення\(f(t)\). Скористайтеся таблицею для оцінки\(\int^{40}_0 f(t) dt\).
|
\(t\) |
0 |
10 |
20 |
30 |
40 |
|
\(f(t)\) |
17 |
22 |
18 |
11 |
35 |
У таблиці наведені значення\(g(x)\).
|
\(x\) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
\(g(x)\) |
140 |
142 |
144 |
152 |
154 |
165 |
200 |
Використовуйте таблицю для оцінки
| а.\(\int^3_0 g(x) dx\) | б\(\int^6_3 g(x) dx\) | c.\(\int^6_0 g(x) dx\) |
Які одиниці для «площі» прямокутника із заданими одиницями основи та висоти?
| Базові одиниці | Одиниці вимірювання висоти | Одиниці «Площа» |
|
миль в секунду |
секунд |
|
|
годин |
доларів на годину |
|
|
квадратних футів |
стопи |
|
|
кіловат |
годин |
|
|
будинки |
людей на будинок |
|
|
харчування |
харчування |
У задачах 15 — 17 представляють площу кожної обмеженої області як певний інтеграл, а геометрію використовують для визначення значення певного інтеграла.
15. Область, обмежена\(y = 2x \),\(x\) вісь —, лінія\(x = 1\), і\(x = 3\).
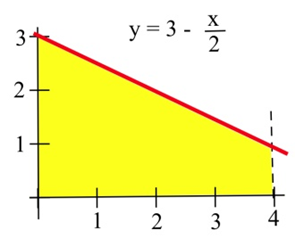
16. Регіон\(y = 4 – 2x \), обмежений\(x\) віссю —та\(y\) віссю —.
17. Затінена область на графіку праворуч.
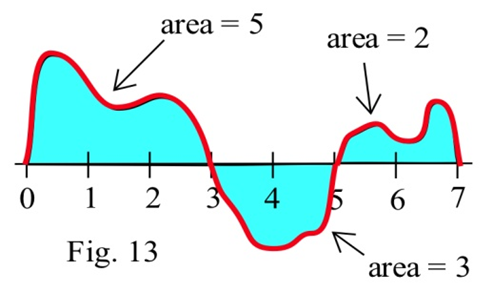
Використовуючи графік\(f\) показаних і заданих областей декількох регіонів, оцініть:
(а)\(\int^3_0 f(x) dx\)
(б)\(\int^5_3 f(x) dx\)
(c)\(\int^7_5 f(x) dx\)
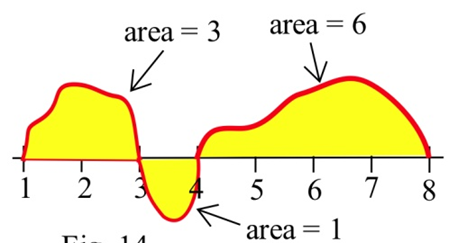
Використовуючи графік\(f\) показаних і заданих областей декількох регіонів, оцініть:
(а)\(\int^3_1 g(x) dx\)
(б)\(\int^4_3 g(x) dx\)
(c)\(\int^8_4 g(x) dx\)
(г)\(\int^8_1 g(x) dx\)
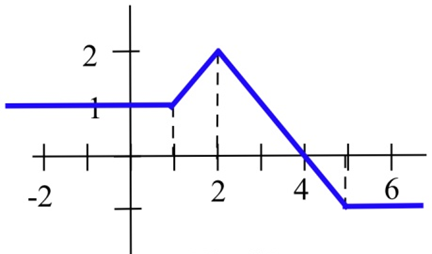
Використовуйте графік для оцінки:
(а)\(\int^1_{-2} h(x) dx\)
(б)\(\int^6_4 h(x) dx\)
(c)\(\int^6_{-2} h(x) dx\)
(г)\(\int^4_{-2} h(x) dx\)
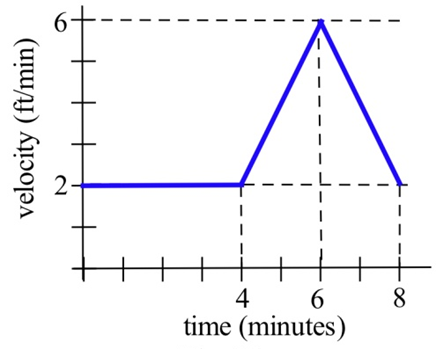
Ваша швидкість по прямій дорозі показана праворуч. Як далеко ви подорожували за 8 хвилин?
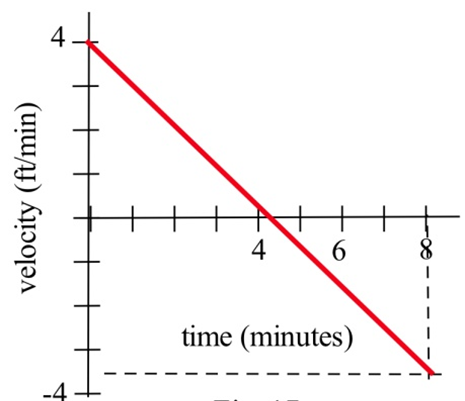
Ваша швидкість по прямій дорозі показана нижче. Скільки футів ви пройшли за 8 хвилин?
У задачах 23 - 26 одиниці\(x\) наведені за і за\(f(x)\). Дайте одиниці\(\int^b_a f(x) dx\).
23. \(x\)це час в «секундах»,\(f(x)\) а швидкість в «метрах в секунду».
24. \(x\)це час в «годині», і\(f(x)\) є витратою в «галонів на годину».
25. \(x\)це положення в «футах», і\(f(x)\) є областю в «квадратних футах».
26. \(x\)це позиція в «дюймах», і\(f(x)\) є щільністю в «фунтах на дюйм».
У задачах 27 — 31 представляють область з певним інтегралом і використовують технологію, щоб знайти приблизну відповідь.
27. Область, обмежена\(y = x^3\),\(x\) вісь —, лінія\(x = 1\), і\(x = 5\).
28. Регіон, обмежений\(y = \sqrt{x}\),\(x\) віссю —і лінія\(x = 9\).
29. Заштрихована область показана праворуч.
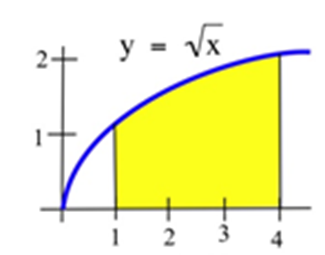
30. Затінена область внизу.
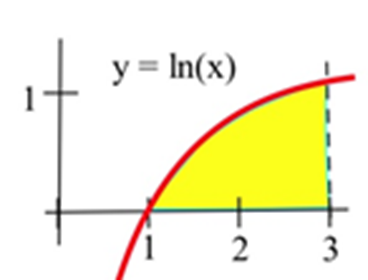
31. Розглянемо певний інтеграл\(\int^3_0 (3+x) dx\).
(а) Використовуючи шість прямокутників, знайдіть ліву суму Рімана для цього визначеного інтеграла.
(b) Використовуючи шість прямокутників, знайдіть праву суму Рімана для цього визначеного інтеграла.
(c) Використовуючи геометрію, знайти точне значення цього певного інтеграла.
Розглянемо певний інтеграл\(\int^2_0 x^3 dx\).
(а) Використовуючи чотири прямокутники, знайдіть ліву суму Рімана для цього визначеного інтеграла.
(b) Використовуючи чотири прямокутники, знайдіть праву суму Рімана для цього визначеного інтеграла.
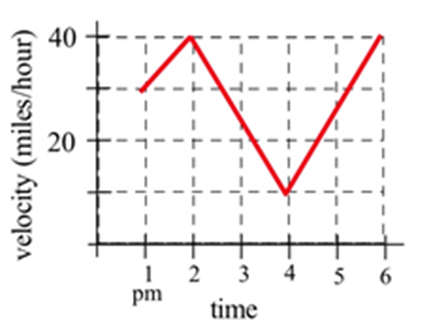
Запишіть загальну відстань, пройдену автомобілем, в графіку між 1 вечора і 4 вечора як певний інтеграл і оцініть значення інтеграла.
Задачі 34 — 41 відносяться до\(f\) показаного графіку.
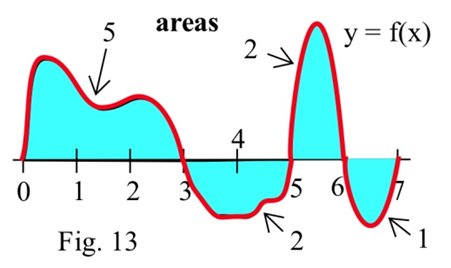
Використовуйте графік для визначення значень певних інтегралів. (Жирним шрифтом цифри позначають площу кожного регіону.)
| 34. \(\int^3_0 f(x) dx\) | 35. \(\int^5_3 f(x) dx\) | 36. \(\int^2_2 f(x) dx\) | 37. \(\int^7_6 f(w) dw\) |
| 38. \(\int^5_0 f(x) dx\) | 39. \(\int^7_0 f(x) dx\) | 40. \(\int^6_3 f(t) dt\) | 41. \(\int^7_5 f(x) dx\) |
Задачі 42 — 47 відносяться до\(g\) показаного графіку.
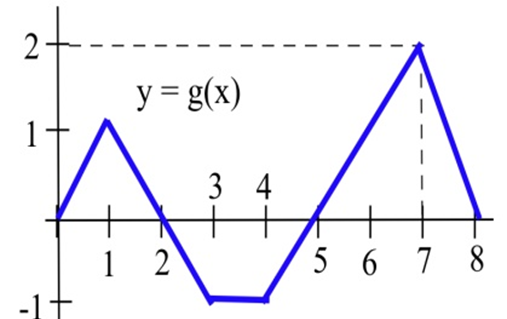
Використовуйте графік для оцінки інтегралів.
| 42. \(\int^2_0 g(x) dx\) | 43. \(\int^3_1 g(t) dt\) | 44. \(\int^5_0 g(x) dx\) |
| 45. \(\int^8_0 g(s) ds\) | 46. \(\int^3_0 2g(t) dt\) | 47. \(\int^8_5 1+g(x) dx\) |
3.2 Вправи
У задачах 1 — 5 перевірте, що\(F(x)\) це антипохідне цілого,\(f(x)\) і використовуйте частину 2 Фундаментальної теореми для оцінки певних інтегралів.
| 1. \(\int^1_0 2x dx, F(x) = x^2 + 5\) | 2. \(\int^4_1 3x^2 dx, F(x) = x^3 + 2\) | 3. \(\int^3_1 x^2 dx, F(x) = \frac{1}{3} x^3\) |
| 4. \(\int^3_0 (x^2+4x - 3) dx , F(x) = \frac{1}{3} x^3 + 2x^2 – 3x\) | 5. \(\int^5_1 \frac{1}{x} dx, F(x) = \ln ( x )\) |
Дано\(A(x) = \int^x_0 2t dt\), знахідка\(A'(x)\)
Дано\(A(x) = \int^x_0 (3-t^2) dt\), знахідка\(A'(x)\)
Нехай\(A(x) = \int^x_0 f(t) dt\) для функції графіки тут.
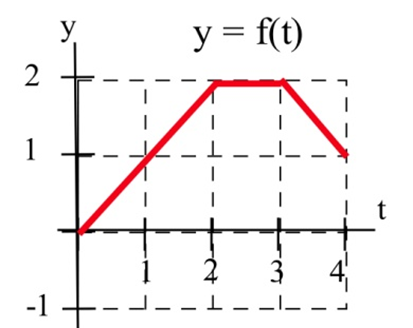
Оцінювати\(A'(1)\),\(A'(2)\),\(A'(3)\).
Для задач 9-10 показано наведений графік\(g'(x)\). Використовуйте його ескіз графіка\(g(x)\), який задовольняє\(g(0) = 0\).
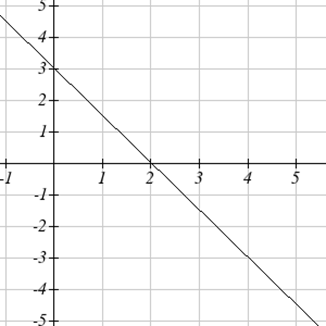
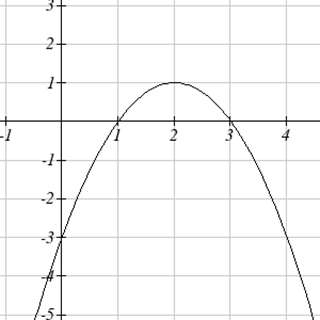
10.
3.3 Вправи
Для задач 1-10 знайдіть вказане антипохідне.
| 1. \(\int (x^3 - 14x + 5) dx\) | 2. \(\int (2.5x^5-x-1.25) dx\) |
| 3. \(\int 12.3 dy\) | 4. \(\int \pi^2 dw\) |
| 5. \(\int e^P dP\) | 6. \(\int \left( \sqrt{x} + e^x - \frac{1}{4x^3} \right) dx\) |
| 7. \(\int \frac{1}{x} dx\) | 8. \(\int \frac{1}{x^2} dx\) |
| 9. \(\int (x-2)(x+2) dx\) | 10. \(\int \frac{t^5-t^2}{t} dt\) |
Для задач 11-18 знайти антипохідне цілого і використовувати фундаментальну теорему для оцінки певного інтеграла.
| 11. \(\int^5_2 3x^2 dx\) | 12. \(\int^2_{-1} x^2 dx\) | 13. \(\int^3_1 (x^2+4x-3) dx\) | 14. \(\int^e_1 \frac{1}{x} dx\) |
| 15. \(\int^{100}_{25} \sqrt{x} dx\) | 16. \(\int^5_3 \sqrt{x} dx\) | 17. \(\int^{10}_1 \frac{1}{x^2} dx\) | 18. \(\int^{1000}_1 \frac{1}{x^2} dx\) |
Для завдань 19 - 21 знайдіть область, показану на малюнку.
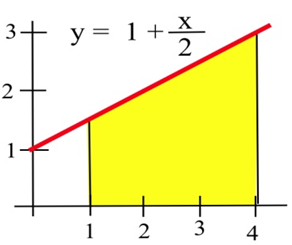
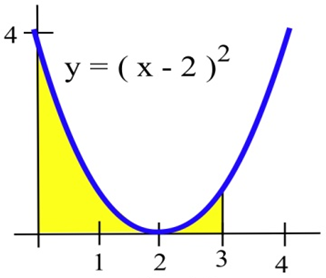
20.
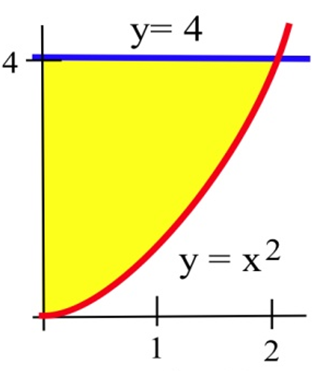
3.4 Вправи
Для задач 1-8 знайдіть вказане антипохідне.
| 1. \(\int \frac{1}{(4x+1)^3} dx\) | 2. \(\int e^{100x} dx\) |
| 3. \(\int (1.0003)^{12t} dt\) | 4. \(\int \frac{e^{10/x}}{x^2} dx\) |
| 5. \(\int \sqrt{w+5} dw\) | 6. \(\int 6x^2 \sqrt{3x^3-1} dx\) |
| 7. \(\int \frac{dx}{x\ln x}\) | 8. \(\int \frac{x-3}{x^2-6x+5} dx\) |
Для задач 9-12 знайти антипохідне цілого і використовувати фундаментальну теорему для оцінки певного інтеграла.
| 9. \(\int^2_{-2} \frac{2x}{1+x^2} dx\) | 10. \(\int^1_0 e^{2x} dx\) | 11. \(\int^{4}_2 (x-2)^3 dx\) | 12. \(\int^1_0 x \sqrt{1-x^2} dx\) |
3.5 Вправи
У задачах 1—4\(dv\) задається функція\(u\) або. Знайдіть шматок\(u\) або\(dv\) який не задано, розрахуйте\(du\) та\(v\) застосуйте формулу інтеграції по частинам.
| 1. \(\int 12x \cdot \ln(x) dx\) | \(u = \ln(x)\) | 2. \(\int x \cdot e^{–x} dx\) | \(u = x\) |
| 3. \(\int x^4 \ln(x) dx\) | \(dv = x^4 dx\) | 4. \(\int x \cdot (5x + 1)^{19} dx\) | \(u = x\) |
У задачах 5 - 10 оцінюємо інтеграли
| 5. \(\int^1_0 \frac{x}{e^{3x}} dx\) | 6. \(\int^1_0 10x \cdot e^{3x} dx\) | 7. \(\int^3_1 \ln (2x + 5) dx\) |
| 8. \(\int x^3 \ln (5x) dx\) | 9. \(\int x \ln (x + 1) dx\) | 10. \(\int^2_1 \frac{\ln (x)}{x^2} dx\) |
Для завдань 11 - 14 інтегрують кожну функцію.
| 11. \(\int \frac{1}{4-x^2}\) | 12. \(\int \frac{2}{9-x^2}\) | 13. \(\int \sqrt{4+x^2}\) | 14. \(\int \sqrt{9+x^2}\) |
3.6 Вправи
У задачах 1 — 4 використовуйте значення в таблиці для оцінки площ.
| \(x\) | \(f(x)\) | \(g(x)\) | \(h(x)\) |
|
0 |
5 |
2 |
5 |
|
1 |
6 |
1 |
6 |
|
2 |
6 |
2 |
8 |
|
3 |
4 |
2 |
6 |
|
4 |
3 |
3 |
5 |
|
5 |
2 |
4 |
4 |
|
6 |
2 |
0 |
2 |
1. Оцініть площу між\(f\) і\(g\), між\(x = 0\) і\(x = 4\).
2. Оцініть площу між\(g\) і\(h\), між\(x = 0\) і\(x = 6\).
3. Оцініть площу між\(f\) і\(h\), між\(x = 0\) і\(x = 4\).
4. Оцініть площу між\(f\) і\(g\), між\(x = 0\) і\(x = 6\).
Оцініть площа показаного острова
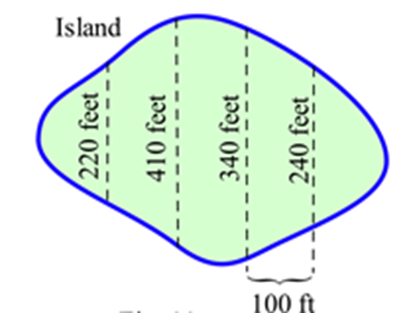
У задачах 6 — 15 знайти площу між графами\(f\) та\(g\) for\(x\) у заданому інтервалі. Не забудьте намалювати графік!
| 6. \(f(x) = x^2 + 3 \),\(g(x) = 1\) і\(–1 \leq x \leq 2\). |
| 7. \(f(x) = x^2 + 3 \),\(g(x) = 1 + x\) і\(0 \leq x \leq 3\). |
| 8. \(f(x) = x^2 \),\(g(x) = x\) і\(0 \leq x \leq 2\). |
| 9. \(f(x) = (x –1)^2 \),\(g(x) = x + 1\) і\(0 \leq x \leq 3\). |
| 10. \(f(x) = \frac{1}{x}\),\(g(x) = x\) і\(1 \leq x \leq e\). |
| 11. \(f(x) = \sqrt{x}\),\(g(x) = x\) і\(0 \leq x \leq 4\). |
| 12. \(f(x) = 4 – x^2 \),\(g(x) = x + 2\) і\(0 \leq x \leq 2\). |
| 13. \(f(x) = e^x\),\(g(x) = x\) і\(0 \leq x \leq 2\). |
| 14. \(f(x) = 3 \),\(g(x) = \sqrt{1-x^2}\) і\(0 \leq x \leq 1\). |
| 15. \(f(x) = 2 \),\(g(x) = \sqrt{4-x^2}\) і\(–2 \leq x \leq 2\). |
Для задач 16-18 знайти обсяг твердого тіла, отриманого обертанням зазначеної області навколо\(x\) осі.
16. Регіон під\(f(x) = x^2 + 3\) для\(–1 \leq x \leq 2\).
17. Регіон під\(f(x) = 4 – x^2\) для\(0 \leq x \leq 2\).
18. Регіон під\(f(x) = \frac{1}{x}\) для\(1 \leq x \leq 2\).
У задачах 19 і 20 використовуйте значення в таблиці для оцінки середніх значень.
| \(x\) | \(f(x)\) | \(g(x)\) |
|
0 |
5 |
2 |
|
1 |
6 |
1 |
|
2 |
6 |
2 |
|
3 |
4 |
2 |
|
4 |
3 |
3 |
|
5 |
2 |
4 |
|
6 |
2 |
0 |
19. Оцініть середнє значення\(f\) на інтервалі [0, 6].
20. Оцініть середнє значення\(g\) на інтервалі [0, 6].
У задачах 21 — 26 знайти середнє значення\(f\) на заданому інтервалі.
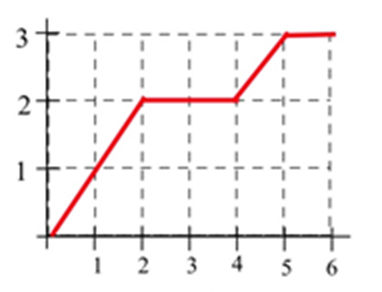
21. \(f(x)\)з графіка для\(0 \leq x \leq 2\).
22. \(f(x)\)з графіка для\(0 \leq x \leq 4\).
23. \(f(x)\)з графіка для\(1 \leq x \leq 6\).
24. \(f(x)\)з графіка для\(4 \leq x \leq 6\).
25. \(f(x) = 2x + 1\)для\(0 \leq x \leq 4\).
26. \(f(x) = x^2\)для\(0 \leq x \leq 2\).
Графік показує швидкість руху автомобіля під час 5-годинної поїздки.
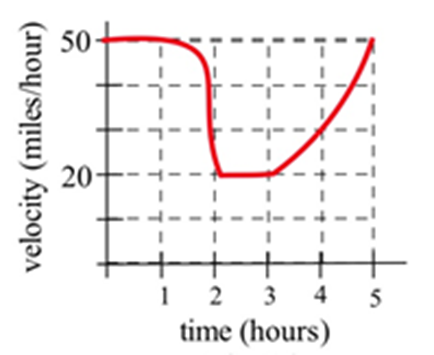
(а) Оцініть, наскільки далеко автомобіль проїхав протягом 5 годин.
(б) З якою постійною швидкістю слід їздити, щоб пройти однакову відстань за 5 годин?
Графік показує кількість телефонних дзвінків за хвилину у великій компанії.
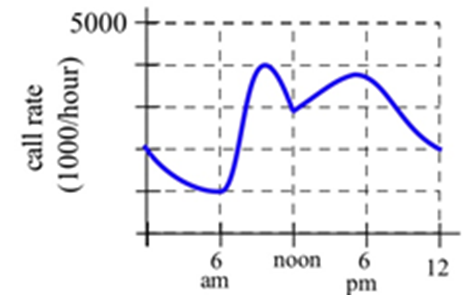
Оцініть середню кількість дзвінків за хвилину
(а) З 8 ранку до 5 вечора.
(б) З 9 ранку до 13 години вечора.
3.7 Вправи
Функції попиту і пропозиції на певний товар задаються\(p = 150 - .5q\) і\(p = .002q^2+1.5\), де\(p\) знаходиться в доларах і\(q\) є кількістю позицій.
(а) Яка функція попиту?
(b) Знайти рівноважну ціну та кількість
(c) Знайдіть загальний прибуток від торгівлі за рівноважною ціною.
Все ще думаючи про продукт з вправи 1, з його функціями попиту та пропозиції, припустимо, що ціна встановлена штучно на рівні 70 доларів (що вище рівноважної ціни).
(а) Знайдіть кількість, що постачається та кількість, необхідну за цією ціною.
(b) Обчислити споживчий надлишок за цією ціною, використовуючи необхідну кількість.
(c) Обчислити надлишок виробника за цією ціною, використовуючи необхідну кількість (чому?).
(d) Знайдіть загальний прибуток від торгівлі за цією ціною.
(е) Що ви спостерігаєте?
Коли ціна певного товару становить 40 доларів, можна продати 25 предметів. Коли ціна того ж товару коштує 20 доларів, можна продати 185 одиниць товару. З іншого боку, коли ціна цього товару складе 40 доларів, буде випущено 200 найменувань. Але коли ціна цього товару складе 20 доларів, буде випущено всього 100 найменувань. Використовуйте цю інформацію для пошуку функцій попиту та пропозиції (припустимо для простоти, що функції лінійні) та обчислення надлишку споживача та виробника за рівноважною ціною.
Знайдіть теперішні та майбутні значення безперервного потоку доходів у розмірі 5000 доларів на рік протягом 12 років, якщо гроші можуть заробляти 1,3% річних відсотків, що складаються безперервно.
Знайти поточну вартість безперервного потоку доходу $40,000 на рік протягом 35 років, якщо гроші можуть заробити
(a) 0,8% річних відсотків, що посилюються постійно,
(б) 2,5% річних відсотків, що складаються безперервно,
(c) 4,5% річних відсотків, що посилюються постійно.
Знайдіть теперішню вартість безперервного потоку доходу\(F(t) = 20+t\), де\(t\) знаходиться в роках і\(F\) знаходиться в десятках тисяч доларів на рік, протягом 10 років, якщо гроші можуть заробляти 2% річних відсотків, що складаються безперервно.
Знайдіть теперішню вартість безперервного потоку доходу\(F(t) = 12+0.3t^t\), де\(t\) знаходиться в роках і\(F\) знаходиться в тисячах доларів на рік, протягом 8 років, якщо гроші можуть заробляти 3,7% річних відсотків, що складаються безперервно.
Знайдіть майбутню вартість безперервного потоку доходу\(F(t) = 8500+ \sqrt{640t+100}\), де\(t\) знаходиться в роках і\(F\) знаходиться в доларах на рік, протягом 15 років, якщо гроші можуть заробляти 6% річних відсотків, що складаються безперервно.
Очікується, що бізнес буде приносити дохід з постійною ставкою 25 000 доларів на рік протягом наступних восьми років. Гроші можуть заробляти 3,4% річних відсотків, що посилюються безперервно. Бізнес продається за 153 000 доларів. Це гарна угода?
3.8 Вправи
У задачах 1 — 4 перевірте, чи функція\(y\) є розв'язком заданого диференціального рівняння.
| 1. \(y' + 3y = 6\). \(y = e^{–3x} + 2\). | 2. \(y' – 2y = 8\). \(y = e^{2x} – 4\). |
| 3. \(y' = – x/y\). \(y = \sqrt{7-x^2}\). | 4. \(y' = x – y\). \(y = x – 1 + 2e^{–x}\). |
У задачах 5 — 8 перевірте, що функція\(y\) є розв'язком заданої задачі початкового значення.
5. \(y' = 6x^2 – 3\)і\(y(1) = 2 \). \(y = 2x^3 – 3x + 3\).
6. \(y' = 6x + 4\)і\(y(2) = 3\). \(y = 3x^2 + 4x – 17\).
7. \(y' = 5y\)і\(y(0) = 7\). \(y = 7e^{5x}\).
8. \(y' = –2y\)і\(y(0) = 3\). \(y = 3e^{–2x}\).
У задачах 9 — 12 наведено сімейство розв'язків диференціального рівняння. Знайти значення константи\(C\) так, щоб рішення задовольняло умові початкового значення.
| 9. \(y' = 2x\)і\(y(3) = 7\). \(y = x^2 + C\). | 10. \(y' = 3x^2 – 5\)і\(y(1) = 2\). \(y = x^3 – 5x + C\). |
| 11. \(y' = 3y\)і\(y(0) = 5\). \(y = Ce^{3x}\). | 12. \(y' = –2y\)і\(y(0) = 3\). \(y = Ce^{–2x}\). |
У задачах 13 — 18 розв'яжіть диференціальне рівняння. (Припустимо, що\(x\) і\(y\) обмежені так, що поділ на нуль не відбувається.)
| 13. \(y' = 2xy\) | 14. \(y' = x/y\) | 15. \(xy' = y + 3\) |
| 16. \(y' = x^2y + 3y\) | 17. \(y' = 4y\) | 18. \(y' = 5(2 – y)\) |
У задачах 19 — 22 розв'язують початкове значення відокремлюваних диференціальних рівнянь.
19. \(y' = 2xy\)для\(y(0) = 3\),\(y(0) = 5\), і\(y(1) = 2\).
20. \(y' = x/y\)для\(y(0) = 3\),\(y(0) = 5\), і\(y(1) = 2\).
21. \(y' = 3y\)для\(y(0) = 4\),\(y(0) = 7\), і\(y(1) = 3\).
22. \(y' = –2y\)для\(y(0) = 4\),\(y(0) = 7\), і\(y(1) = 3\).
Темпи приросту населення,\(P(t)\) яке починається з 3000 чоловік і збільшується на 4% на рік\(P '(t) = 0.0392 \cdot P(t)\). Розв'яжіть диференціальне рівняння і використовуйте рішення для оцінки чисельності населення в 20 років.
Темпи приросту населення,\(P(t)\) яке починається з 5000 чоловік і збільшується на 3% на рік\(P '(t) = 0.0296 \cdot P(t)\). Розв'яжіть диференціальне рівняння і використовуйте рішення для оцінки чисельності населення в 20 років.
За оцінками виробника, вона може продати максимум 130 тисяч мобільних телефонів у місті. Завдяки значній рекламі, її загальні продажі зростають зі швидкістю, пропорційною відстані нижче цієї верхньої межі. Якщо вона виходить на новий ринок, і через 6 місяців її загальний обсяг продажів становить 59 тисяч телефонів, знайдіть формулу загального обсягу продажів (у тисячах)\(t\) місяців після виходу на ринок і використовуйте це для оцінки загального обсягу продажів на кінець першого року.
Температура індички в духовці буде рости як обмежене зростання. Індичка починається з 40 градусів за Фаренгейтом і поміщається в духовку 350 градусів. Через 30 хвилин температура індички піднялася до 55 градусів. Скільки часу пройде, поки температура індички не досягне 165 градусів?
На ринок представлений новий стільниковий телефон. Прогнозується, що продажі будуть рости логістично. Виробник підраховує, що вони можуть продати максимум 100 тисяч стільникових телефонів. Після того, як було продано 44 тисячі стільникових телефонів, продажі збільшуються на 4 тисячі телефонів на місяць. Скористайтеся цим, щоб оцінити загальний обсяг продажів на кінець першого року.
Біологи заповнили озеро 400 рибами і оцінили вантажопідйомність озера в 8000 риб. Кількість риби за перший рік збільшилася втричі. Скільки часу знадобиться чисельність населення, щоб збільшити до 4000?
