3.8: Додатки для бізнесу

Last updated
Save as PDF

Page ID: 60236

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Надлишок споживачів і виробників

Ось крива попиту та пропозиції на товар. Що таке?

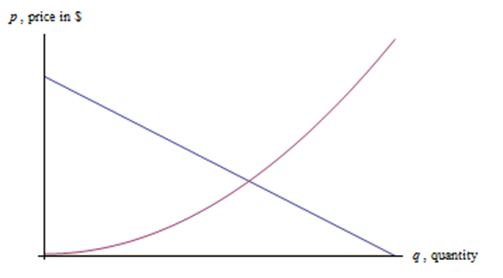
Крива попиту зменшується - нижчі ціни пов'язані з більшими обсягами, що затребувані, більш високі ціни пов'язані з меншими обсягами, що затребувані. Криві попиту часто відображаються так, ніби вони лінійні, але немає причин, які вони повинні бути.

Крива пропозиції зростає - нижчі ціни пов'язані з меншою пропозицією, а більш високі ціни пов'язані з більшими обсягами поставок.

Точка, де перетинається крива попиту і пропозиції, називається точкою рівноваги$(q^*, p^*)$.

Припустимо, що ціна встановлюється за рівноважною ціною, так що затребувана кількість дорівнює кількості, що поставляється. Тепер подумайте про людей, які представлені зліва від точки рівноваги. Споживачі зліва були б готові заплатити вищу ціну, ніж їм довелося платити, тому рівноважна ціна заощадила їм гроші. З іншого боку, виробники, представлені зліва, були б готові поставляти ці товари за нижчою ціною - вони заробили більше грошей, ніж очікували. Обидві ці групи закінчилися з додатковими готівками в кишенях!

Графічно кількість додаткових грошей, які опинилися в кишенях споживачів, - це область між кривою попиту та горизонтальною лінією на$p^*$. Це різниця в ціні, підсумована над усіма споживачами, які витратили менше, ніж вони очікували — певний інтеграл. Зверніть увагу, що оскільки площа під горизонтальною лінією є прямокутником, ми можемо спростити інтеграл площі:\[ \int\limits_0^{q^*} \left( d(q)-p^*\right)\, dq = \int\limits_0^{q^*} d(q)\, dq - \int\limits_0^{q^*} p^*\, dq = \int\limits_0^{q^*} d(q)\, dq - p^*q^*.\nonumber \]

Кількість додаткових грошей, які опинилися в кишенях виробників, - це область між кривою пропозиції та горизонтальною лінією на$p^*$. Це різниця в ціні, підсумована над усіма виробниками, які отримали більше, ніж очікували. Подібно до споживчого надлишку, цей інтеграл можна спростити:\[ \int\limits_0^{q^*} \left( p^*-s(q) \right)\, dq = \int\limits_0^{q^*} p^*\, dq - \int\limits_0^{q^*} s(q)\, dq = p^*q^* - \int\limits_0^{q^*} s(q)\, dq.\nonumber \]

Надлишок споживачів і виробників

Задано функцію попиту$p = d(q)$ і функцію пропозиції$p = s(q)$, а також точку рівноваги$(q^*, p^*)$

Споживчий надлишок\[\int\limits_0^{q^*} d(q)\, dq - p^*q^*.\nonumber \]
Надлишок виробника\[p^*q^* - \int\limits_0^{q^*} s(q)\, dq.\nonumber \]
Сума споживчого профіциту та надлишку виробника - це загальний прибуток від торгівлі.

Які одиниці споживчого і виробничого надлишку? Одиниці (ціна за одиницю товару) (кількість предметів) = гроші!

Приклад$\PageIndex{1}$

Припустимо, попит на товар задається$ p=d(q)=-0.8q+150 $ і пропозиція на один і той же товар задається$ p=s(q)=5.2q $. Для обох функцій$q$ - це кількість і$p$ ціна, в доларах.

Знайдіть точку рівноваги.
Знайдіть споживчий надлишок за рівноважною ціною.
Знайдіть надлишок виробника за рівноважною ціною.

Рішення

Точка рівноваги - це місце, де функції попиту та пропозиції рівні. \[ \begin{align*} -0.8q+150 & = 5.2q \\ 150 & = 6.0q \\ q & = \frac{150}{6} \\ q & = 25 \end{align*} \nonumber \]
Рівноважна кількість - 25 предметів. Щоб знайти відповідну рівноважну ціну, ми можемо використовувати рівняння попиту або пропозиції.

$s(25) = 5.2(25) = 130$. Рівноважна ціна - 130 доларів.
Споживчий надлишок\[ \begin{align*} \int_0^{25} (-0.8q+150)\, dq - (130)(25) & = \left[-0.8 \frac{q^2}{2} + 150 q\right]_0^{25} - 3250 \\ & = \left(-0.4\left(25^2\right) + 150(25)\right) - \left(-0.4\left(0^2\right) + 150(0)\right) - 3250 \\ & = 3500 - 0 - 3250 \\ & = \$250 \end{align*} \nonumber \]
Надлишок виробника\[ \begin{align*} (130)(25) - \int_0^{25} 5.2q\, dq & = 3250 - \left[5.2 \frac{q^2}{2}\right]_0^{25} \\ & = 3250 - \left(\left(2.6\left(25^2\right)\right) - \left(2.6\left(0^2\right)\right)\right) \\ & = 3250 - (1625 - 0) \\ & = \$1625 \end{align*} \nonumber \]

Приклад$\PageIndex{2}$

Припустимо, попит на товар задається$ p=d(q)=300-5q $ і пропозиція на один і той же товар задається$ p=s(q)=q^2 $. Для обох функцій$q$ - це кількість і$p$ ціна, в доларах.

Знайдіть точку рівноваги.
Знайдіть споживчий надлишок за рівноважною ціною.
Знайдіть надлишок виробника за рівноважною ціною.

Рішення

Це квадратично, тому ми можемо переставити рівняння так, щоб одна сторона дорівнювала нулю:$q^2 + 5q - 300 = 0$.
Ми могли б вирішити це за допомогою квадратного рівняння:$q = \frac{-5 \pm \sqrt{5^2-4(1)(-300)}}{2(1)}$

або ми могли б врахувати:$(q+20)(q-15)=0$, так$q =-20$ чи$q = 15$.

Ми хочемо позитивного рішення. Рівноважна кількість - 15 предметів. Рівноважна ціна є$s(15) = 15^2 = \$225$.
Споживчий надлишок\[ \begin{align*} \int_0^{15} (300-5q)\, dq - (225)(15) & = \left[300q - 5\frac{q^2}{2}\right]_0^{15} - 3375 \\ & = \left(300(15) - 2.5\left(15^2\right)\right) - \left(300(0) - 2.5\left(0^2\right)\right) - 3375 \\ & = 3937.5 - 0 - 3375 \\ & = \$562.50 \end{align*} \nonumber \]
Надлишок виробника\[ \begin{align*} (225)(15) - \int_0^{15} q^2\, dq & = 3375 - \left[\frac{q^3}{3}\right]_0^{15}s \\ & = 3375 - \left(\left(\frac{15^3}{3}\right) - \left(\frac{0^3}{3}\right)\right) \\ & = 3375 - (1125 - 0) \\ & = \$2250 \end{align*} \nonumber \]

Приклад$\PageIndex{3}$

У таблицях нижче наведено інформацію про функції попиту та пропозиції на товар. Для обох функцій$q$ - це кількість і$p$ ціна, в доларах.

q	0	100	200	300	400	500	600	700
р	70	61	53	46	40	35	31	28

q	0	100	200	300	400	500	600	700
р	14	21	28	33	40	47	54	61

Що таке? Тобто, яка таблиця представляє попит, а яка - пропозиція?
Що таке рівноважна ціна і кількість?
Знайдіть надлишок споживача та виробника за рівноважною ціною.

Рішення

Перша таблиця показує зниження ціни, пов'язане зі збільшенням кількості; це функція попиту.
Для обох функцій$q = 400$ пов'язана з$p = 40$; рівноважна ціна становить 40 доларів, а рівноважна кількість - 400 одиниць. Зверніть увагу, що нам пощастило тут, тому що точка рівноваги насправді є однією з показаних точок. У багатьох випадках з таблицею нам доведеться оцінити.
Споживчий надлишок використовує функцію попиту, яка виходить з першої таблиці. Доведеться наблизити значення інтеграла за допомогою прямокутників. Є 4 прямокутника, і давайте виберемо ліві кінцеві точки.
Споживчий надлишок є\[ \begin{align*} \int\limits_0^{400} \text{(demand)}\, dq-(40)(400)\approx & \\ (100)(70+61+53+46)-(40)(400) & = \$7000 \end{align*} \nonumber \] Таким чином, споживчий надлишок становить близько 7000 доларів.

Надлишок виробника використовує функцію постачання, яка виходить з другої таблиці. Давайте вирішимо використовувати ліві кінцеві точки для цього інтеграла також.

Надлишок виробника є\[ \begin{align*} (40)(400)-\int\limits_0^{400} \text{(supply)}\, dq \approx & \\ (40)(400)-(100)(14+21+28+33) & = \$6400 \end{align*} \nonumber \] Таким чином, надлишок виробника становить близько 6400 доларів.

Безперервний потік доходу

У попередньому обчисленні ви дізналися про складні відсотки в тій дійсно простій ситуації, коли ви внесли єдиний депозит на відсотковий рахунок і нехай він сидить без турбот, заробляючи відсотки, протягом деякого періоду часу. Нагадаємо:

Складні процентні формули

$P$Дозволяти основною (початкові інвестиції),$r$ бути річна процентна ставка, виражена у вигляді десяткової коми, і$A(t)$ сума на рахунку в кінці$t$ років.

Складання$n$ разів на рік

\[ A(t) = P\left(1+\frac{r}{n}\right)^{nt} \nonumber \]

Посувається безперервно

\[ A(t)=Pe^{rt} \nonumber \]

Якщо ви використовуєте цю формулу, щоб знайти, який рахунок буде коштувати в майбутньому,$t \gt 0$ і$A(t)$ називається майбутнім значенням.

Якщо ви використовуєте формулу, щоб знайти те, що вам потрібно внести сьогодні, щоб мати певне значення$P$ десь у майбутньому,$t \lt 0$ і$A(t)$ називається теперішньою вартістю.

Можливо, ви також дізналися дещо складніші формули ануїтету, щоб мати справу з дещо складнішими ситуаціями - коли ви робите рівні депозити однаково розташовані в часі.

Але реальне життя зазвичай не така акуратна.

Обчислення дозволяє нам обробляти ситуації, коли депозити безперервно надходять на рахунок, який заробляє відсотки. Поки ми можемо моделювати потік доходу за допомогою функції, ми можемо використовувати певний інтеграл для обчислення теперішньої та майбутньої вартості безперервного потоку доходів. Ідея тут полягає в тому, що кожен трохи доходу в майбутньому потрібно помножити на експоненціальну функцію, щоб повернути його до сьогодення, а потім ми додамо їх усі (певний інтеграл).

Безперервний потік доходу

Припустимо, гроші можуть заробляти відсотки за річною процентною ставкою$r$, compounded continuously. Let $F(t)$ be a continuous income function (in dollars per year) that applies between year 0 and year $T$.

Тоді поточна вартість цього потоку доходів задається\[ PV = \int\limits_0^T F(t)e^{-rt}\, dt. \nonumber \]

Майбутнє значення можна обчислити за звичайною складною формулою відсотків\[ FV = PVe^{rt}. \nonumber \]

Це корисний спосіб порівняти дві інвестиції - знайти теперішню вартість кожної, щоб побачити, яка коштує більше сьогодні.

Приклад$\PageIndex{4}$

У вас є можливість купити бізнес, який буде заробляти 75 000 доларів на рік безперервно протягом наступних восьми років. Гроші можна заробляти 2,8% на рік, що посилюється безперервно. Чи варто цей бізнес його закупівельною ціною $630 000?

Рішення

По-перше, зверніть увагу, що нам все одно доведеться зробити деякі спрощуючі припущення. Ми повинні припустити, що процентні ставки залишатимуться постійними протягом цілих восьми років. Ми також повинні припустити, що 75 000 доларів на рік надходять постійно, як кран капає долари в бізнес. Жодне з цих припущень не може бути точним.

Але рухаємося далі: теперішня вартість 630 000 доларів - це, ну, 630 000 доларів. Це одна інвестиція, де ми вклали наші $630 000 в банк і нехай він сидить там.

Щоб знайти теперішню вартість бізнесу, ми думаємо про нього як про потік доходу. Функція$F(t)$ в даному випадку становить постійну 75 000 доларів на рік, так що$F(t) = 75,\!000$. Процентна ставка становить 2,8%, а термін, який нас цікавить, становить 8 років, отже$r = .028$, і$T = 8$:\[ PV=\int\limits_0^8 75000e^{-0.028t}\, dt \approx 537,\!548.75 \nonumber \]

Нинішня вартість бізнесу становить близько 537 500 доларів, що менше, ніж ціна запиту 630 000 доларів, тому це не дуже гарна угода.

Хоча цей інтеграл можна було б зробити за допомогою заміщення, для багатьох інтегралів у цьому розділі ми не маємо методів використання антипохідних або, в деяких випадках, антидериватива не існує. Технологія буде працювати швидко, і вона дасть вам відповідь, який досить хороший.

Приклад$\PageIndex{5}$

Компанія розглядає можливість придбання нової машини для своєї виробничої підлоги. Машина коштує 65 000 доларів. За оцінками компанії, додатковий дохід від машини буде постійним 7000 доларів протягом першого року, потім буде збільшуватися на 800 доларів щороку після цього. Для того щоб купити машину, компанії потрібно переконатися, що вона окупить себе до кінця 8 років цим додатковим доходом. Гроші можна заробляти 1,7% на рік, що посилюється безперервно. Чи повинна компанія купувати машину?

Рішення

Будемо вважати, що дохід буде надходити безперервно протягом 8 років. Ми також припустимо, що процентні ставки залишатимуться постійними протягом цього 8-річного періоду часу.

Нас цікавить поточна вартість машини, яку ми порівняємо з її ціною 65 000 доларів. Нехай$t$ буде час, в роках, з моменту покупки машини. Дохід від машини різний в залежності від часу.

Від$t = 0$ до$t = 1$ (перший рік) дохід постійний 7000 доларів на рік. Від$t = 1$ до$t = 8$, дохід збільшується на $800 щороку; функція потоку доходів$F(t)$ буде$ F(t)=7000+800(t-1)=6200+800t $. Щоб знайти теперішнє значення, нам доведеться розділити інтеграл на дві частини, по одній для кожної з функцій:\[ PV=\int\limits_0^1 7000e^{-0.017t}\, dt + \int\limits_1^8 (6200+800t)e^{-0.017t}\, dt \approx 70166. \nonumber \]

Нинішнє значення більше, ніж вартість машини, тому компанія повинна купувати машину.

Надлишок споживачів і виробників

Приклад\(\PageIndex{1}\)

Приклад\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\)

Складні процентні формули

Складання\(n\) разів на рік

Посувається безперервно

Безперервний потік доходу

Приклад\(\PageIndex{4}\)

Приклад\(\PageIndex{5}\)