4: Функції двох змінних
- Page ID
- 60288
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)
Ідея попереднього обчислення - топологічні карти
Якщо ви коли-небудь походи, ви напевно бачили топографічну карту. Ось частина топографічної карти Стоу, штат Вермонт.
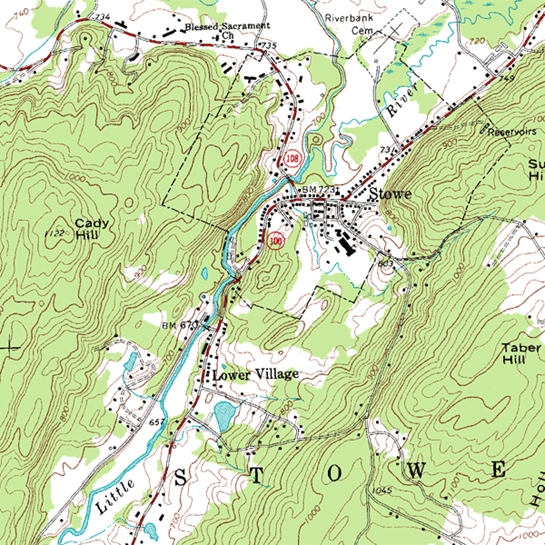
Точки з однаковою висотою пов'язані з кривими, тому ви можете прочитати не тільки своє місцезнаходження схід-захід і північ-південь, але і висоту. Можливо, ви також бачили карти погоди, які використовують той самий принцип - точки з однаковою температурою пов'язані з кривими (ізотермами), або точки з однаковим атмосферним тиском пов'язані з кривими (ізобарами). Ці карти дозволяють читати не тільки місце розташування, але і його температуру або атмосферний тиск.
У цьому розділі ми будемо використовувати ту саму ідею для створення графіків функцій двох змінних.
- 4.2: Обчислення функцій двох змінних
- Тепер, коли ви трохи знайомі з функціями двох змінних, прийшов час почати застосовувати обчислення, щоб допомогти нам вирішити проблеми з ними. У главі 2 ми дізналися про похідну для функцій двох змінних. Похідні розповіли нам про форму функції, і давайте знайдемо локальні max і min - ми хочемо мати можливість зробити те ж саме з функцією двох змінних.
- 4.3: Оптимізація
- Часткові похідні розповідають нам щось про те, де поверхня має локальні максимуми та мінімуми. Пам'ятайте, що навіть в однозмінних випадках були критичні точки, які не були ні максимумами, ні мінімумами — це також справедливо для функцій багатьох змінних. Насправді, як і слід було очікувати, ситуація ще складніше.
