3.9: Диференційні рівняння
- Page ID
- 60250
Диференціальне рівняння - це рівняння, що включає похідну функції. Вони дозволяють нам висловити простим рівнянням зв'язок між величиною та швидкістю зміни.
Банк сплачує 2% відсотків за своїм сертифікатом депозитних рахунків, але стягує щорічну комісію в розмірі 20 доларів США. Напишіть рівняння для швидкості зміни балансу,\( B'(t) \).
Рішення
Якщо на балансі\( B(t) \) є одиниці доларів, то\( B'(t) \) має одиниці доларів на рік. Коли ми думаємо про те, що змінює баланс рахунку, є два фактори:
- Відсотки, які збільшують залишок, і
- Плата, яка зменшує залишок.
З огляду на відсотки, ми знаємо, що з кожним роком баланс буде збільшуватися на 2%, але на 2% від чого? Щороку це буде змінюватися, оскільки ми заробляємо відсотки на будь-якому поточному балансі. Суму приросту ми можемо уявити як 2% від залишку:\( 0.02B(t) \) доларів/рік.
Плата вже має одиниці доларів/рік. Оскільки зараз все має однакові одиниці, ми можемо скласти їх разом і створити рівняння:\[ B'(t)=0.02B(t)-20. \nonumber \]
Результатом є приклад диференціального рівняння. Зверніть увагу, що це конкретне рівняння включає як похідну, так і вихідну функцію, і тому ми не можемо просто знайти\( B(t) \) використання базової інтеграції.
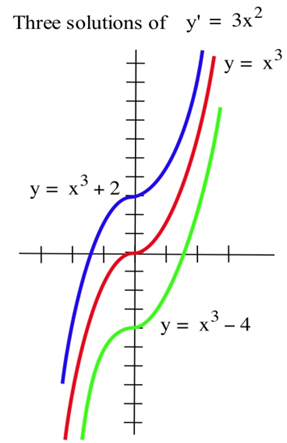
Алгебраїчні рівняння містять константи та змінні, а розв'язки алгебраїчного рівняння зазвичай є числами. Наприклад,\(x = 3\) і\(x = -2\) є розв'язками алгебраїчного рівняння\(x^2 = x + 6\). Диференціальні рівняння містять похідні або диференціали функцій. Розв'язки диференціальних рівнянь є функціями. \(y' = 3x^2\)Диференціальне рівняння має нескінченно багато розв'язків, і два з цих розв'язків - функції\(y = x^3 + 2\) і\(y = x^3 - 4\).
Ви вже розв'язали безліч диференціальних рівнянь: кожен раз, коли ви знайшли антипохідну функції\(f(x)\), ви розв'язували диференціальне рівняння,\(y' = f(x)\) щоб отримати рішення\(y\). Диференціальне рівняння\(y' = f(x)\), однак, є лише початком. Інші програми генерують різні диференціальні рівняння, як у прикладі банківського балансу вище.
Перевірка розв'язків диференційних рівнянь
Незалежно від того, чи диференціальне рівняння легко чи важко вирішити, важливо мати можливість перевірити, чи можливе рішення дійсно задовольняє диференціальному рівнянню.
Можливе рішення алгебраїчного рівняння можна перевірити, поставивши рішення в рівняння, щоб побачити, чи є результат істинним:\(x = 3\) це рішення\(5x + 1 = 16\) since\(5(3) + 1 = 16\) є істинним. Аналогічно, рішення диференціального рівняння можна перевірити шляхом підстановки функції та відповідних похідних у рівняння, щоб побачити, чи є результат істинним:\(y = x^2\) є рішенням\(xy' = 2y\) since\(y' = 2x\) і\(x(2x) = 2\left(x^2\right)\) є істинним.
- \(y = x^2 + 5\)Переконайтеся, що це рішення\(y'' + y = x^2 + 7\) і
- Перевірте, що\(y = x + \frac{5}{x}\) це рішення\(y' + \frac{y}{x} = 2\).
Рішення
- \(y = x^2 + 5\)так\(y' = 2x\) і\(y'' = 2\). Підставляючи ці функції для\(y\) і\(y''\) в диференціальне рівняння\(y'' + y = x^2 + 7\), ми маємо\[y'' + y = (2) + \left(x^2 + 5\right) = x^2 + 7,\nonumber \]\(y = x^2 + 5\) так рішення диференціального рівняння.
- \(y = x + \frac{5}{x}\)так\(y' = 1 - \frac{5}{x^2}\). Підставляючи ці функції для\(y\) і\(y'\) в диференціальному рівнянні\(y' + \frac{y}{x} = 2\), ми маємо\[ y' + \frac{y}{x} = \left(1 - \frac{5}{x^2}\right) + \frac{1}{x}\left(x + \frac{5}{x}\right) = 1 - \frac{5}{x^2} + 1 + \frac{5}{x^2} = 2, \nonumber \] результат, який ми хотіли перевірити.
Роздільні диференціальні рівняння
Диференціальне рівняння називається роздільним, якщо змінні можуть бути відокремлені алгебраїчно так, що всі і\(dx\) є однією стороною рівняння, а всі і\(dy\) знаходяться на іншій стороні рівняння.\(x\)\(y\) Іншими словами, так рівняння має вигляд\( f(x)\, dx=g(y)\, dy \).
Після відокремлення розділені диференціальні рівняння можуть бути вирішені шляхом інтеграції обох сторін рівняння.
Знайдіть рішення\[ y'=\frac{6x+1}{2y}. \nonumber \]
Рішення
Рерайтинг\(y'\) - корисний перший крок:\[ \frac{dy}{dx}=\frac{6x+1}{2y}\nonumber \]
Тепер ми можемо помножити обидві сторони на\(dx\) і на,\(2y\) щоб розділити змінні:\[ 2y\, dy=(6x+1)\, dx \nonumber\]
Інтегруючи кожну сторону, ми\[ \begin{align*} \int 2y\, dy & = \int (6x+1)\, dx \\ y^2+C_1 & = 3x^2+x+C_2 \end{align*} \nonumber \]
Зверніть увагу, що ми можемо об'єднати дві константи, щоб створити нову консолідовану константу\(C\), тому ми зазвичай намагаємося лише поставити константу на правій стороні:\[ y^2=3x^2+x+C. \nonumber \]
Як і очікувалося, існує ціле сімейство розв'язків цього диференціального рівняння.
Задача про початкове значення - це диференціальне рівняння, яке надає додаткову інформацію про початкове або початкове значення функції. Це дозволяє нам потім вирішувати константу і знаходити єдине рішення.
Знайдіть рішення,\( y'=\frac{6x+1}{2y} \) яке задовольняє\( y(2)=3 \).
Рішення
У попередньому прикладі ми знайшли загальне рішення,\( y^2=3x^2+x+C \).
Підставляючи в початковому стані,\(y = 3\) коли\(x = 2\),\[3^2=3(2)^2+2+C,\nonumber \] значить\( 9=12+2+C \), даючи\( C=-5 \).
Рішення\[ y^2=3x^2+x-5. \nonumber \] іноді бажано вирішити для того\(y\), що б поступитися\( y=\pm\sqrt{3x^2+x-5} \), але так як початкова умова мала позитивне\(y\) значення, виділимо позитивне рішення:\[ y=\sqrt{3x^2+x-5}. \nonumber \]
Банк сплачує 2% відсотків за своїм сертифікатом депозитних рахунків, але стягує щорічну комісію в розмірі 20 доларів США. Якщо ви спочатку інвестуєте 3000 доларів, скільки у вас буде через 10 років?
Рішення
Ви можете розпізнати це як приклад з початку розділу, для якого ми встановили рівняння\( B'(t)=0.02B(t)-20 \) або, простіше кажучи,\[ \frac{dB}{dt}=0.02B-20. \nonumber \]
Ми можемо розділити це рівняння множенням на\(dt\) і діленням на весь вираз праворуч:\[ \frac{dB}{0.02B-20}=dt. \nonumber \]
Інтеграція лівої частини цього рівняння вимагає підміни. Нехай\( u=0.02B-20 \), так\( du=0.02\, dB \). Здійснюючи заміну,\[ \begin{align*} \int\frac{dB}{0.02B-20} & = \int\frac{du/0.02}{u} \\ & = \int\frac{1}{u}\frac{du}{0.02} \\ & = \frac{1}{0.02}\int\frac{1}{u}\, du \\ & = \frac{1}{0.02}\ln|u|+C_1\\ & = \frac{1}{0.02}\ln|0.02B-20|+C_1 \end{align*} \nonumber \]
Інтегрувати з правого боку диференціального рівняння простіше:\[\int dt = t+C_2\nonumber \]
Разом це дає нам загальне рішення диференціального рівняння (ми також об'єднуємо їх на\( C \) цьому кроці):\[ \frac{1}{0.02}\ln|0.02B-20|=t+C \nonumber \]
Тепер ми хотіли б вирішити для\(B\). Почніть з множення на 0,02. \[ \begin{align*} \ln|0.02B-20| & = 0.02t+0.02C &\\ \ln|0.02B-20| & = 0.02t+D &\qquad\text{We can rename \( D=0.02C \) for simplicity.}\\ e^{\ln|0.02B-20|} & = e^{0.02t+D} &\qquad\text{Exponentiate both sides: \( e^{\text{left}}=e^{\text{right}} \).}\\ |0.02B-20| & = e^{0.02t+D} &\qquad\text{Use the log rule \( e^{\ln(A)}=A \).}\\ 0.02B-20 & = e^{0.02t+D} &\qquad\text{Since the RHS is always positive, we can drop the abs value.}\\ 0.02B-20 & = e^{0.02t}e^D &\qquad\text{Using the rule \( e^{A+B}=e^Ae^B \).}\\ 0.02B-20 & = ke^{0.02t} &\qquad\text{Rename \( k=e^D \).}\\ B & = \frac{ke^{0.02t}+20}{0.02}=\frac{ke^{0.02t}}{0.02}+1000 &\qquad\text{Add 20 and divide by 0.02.}\\ B & = Ae^{0.02t}+1000 &\qquad\text{Rename \( A=\frac{k}{0.02} \).} \end{align*} \nonumber \]
Нарешті, ми можемо замінити наше початкове значення\(B = 3000\) коли\(t = 0\) вирішувати для константи\(A\):\[ \begin{align*} 3000 & = Ae^{0.02(0)}+1000 \\ A & = 2000 \end{align*} \nonumber \]
Це дає нам рівняння балансу рахунку через\(t\) роки:\[ B(t)=2000e^{0.02t}+1000. \nonumber \]
Щоб знайти баланс через 10 років, ми можемо оцінити це рівняння за адресою\(t = 10\):\[ B(10)=2000e^{0.02(10)}+1000\approx \$3442.81. \nonumber \]
Варто зазначити, що ця відповідь не зовсім правильна. Диференціальні рівняння припускають безперервні зміни, і навряд чи інтерес посилюється безперервно або плата витягується безперервно. Однак відповідь, ймовірно, близька до фактичної відповіді, а диференціальні рівняння забезпечують відносно просту модель складної ситуації.
Моделі зростання
Приклад банківського рахунку продемонстрував одну базову модель зростання: зростання, пропорційне існуючій кількості. Банківські рахунки та населення, як правило, зростають таким чином, якщо не обмежуються. Такий тип зростання називають необмеженим зростанням.
Якщо кількість або популяція y зростає зі швидкістю, пропорційною розміру цієї кількості, вона може бути змодельована з необмеженим зростанням, який має\(r\) диференціальне рівняння:\[ y'=ry, \nonumber \] де константа.
Чисельність населення зростає на 8% щороку. Якщо поточна чисельність населення становить 5000, знайдіть рівняння для населення через\(t\) роки.
Рішення
\[ \begin{align*} \frac{dy}{dt} & = 0.08y &\\ \frac{1}{y}\, dy & = 0.08\, dt &\qquad\text{Separate the variables.}\\ \ln|y| & = 0.08t+C &\qquad\text{Integrate both sides.}\\ e^{\ln|y|} & = e^{0.08t+C} &\qquad\text{Exponentiate both sides.}\\ y & = Ae^{0.08t} &\qquad\text{Simplify both sides, using the tricks we used in the bank example.} \end{align*} \nonumber \]
Тепер підставляємо в початковому стані:\( 5000=Ae^{0.08(0)} \), так\( A=5000 \).
Населення зростатиме за рівнянням\[ y=5000e^{0.08t}. \nonumber \]
Зверніть увагу, що рішення необмеженого рівняння зростання є експоненціальним рівнянням.
Коли товар рекламується сильно, продажі будуть рости дуже швидко, але з часом ринок досягне насичення, а продажі сповільниться. При цьому типі зростання, званому обмеженим зростанням, чисельність населення зростає зі швидкістю, пропорційною відстані від максимального значення.
Якщо величина зростає зі швидкістю, пропорційною відстані від максимального значення,\(M\), it can be modeled with limited growth, which has the differential equation \[ y'=k(M-y), \nonumber \] where \(k\) is a constant, and \(M\) is the maximum size of \(y\).
Вводиться новий стільниковий телефон. За оцінками компанії, вони продадуть 200 тисяч телефонів. Через 1 місяць їх продали 20 тис. Скільки вони продадуть через 9 місяців?
Рішення
У цьому випадку існує максимальна кількість телефонів, які вони розраховують продати, так\(M = 200\) тисячі. Моделюючи продажі\(y\), в тисячах телефонів, ми можемо написати диференціальне рівняння\[ y'=k(200-y). \nonumber \]
Так як це був новий телефон,\( y(0)=0 \). Ми також знаємо продажі через один місяць,\( y(1)=20 \).
Розв'язування диференціального рівняння:\[ \begin{align*} \frac{dy}{dt} & = k(200-y) &\\ \frac{dy}{200-y} & = k\, dt &\qquad\text{Separate the variables.}\\ -\ln|200-y| & = kt+C &\qquad\text{Integrate both sides. On the left use the substitution.}\\ e^{\ln|200-y|} & = e^{-kt+C} &\qquad\text{Multiply both sides by -1, and exponentiate both sides.}\\ 200-y & = Be^{-kt} &\qquad\text{Simplify.}\\ y & = Ae^{-kt}+200 &\qquad\text{Subtract 200, divide by -1, and simplify.} \end{align*} \nonumber \]
Використовуючи початкову умову\( y(0)=0 \),\[ 0=Ae^{-k(0)}+200, \nonumber \] значить\( 0=A+200 \), даючи\( A=-200 \).
Використовуючи значення\( y(1)=20 \):\[ \begin{align*} 20 & = -200e^{-k(t)}+200 &\\ \frac{=180}{-200} & = 0.9=e^{-k} &\qquad\text{Subtract 200 and divide -200.}\\ \ln(0.9) & = \ln\left(e^{-k}\right)=-k &\qquad\text{Take the ln of both sides.}\\ k & = -\ln(0.9)\approx 0.105 &\qquad\text{Divide by -1.} \end{align*} \nonumber \]
Як швидка перевірка розсудливості, це значення є позитивним, як ми очікували, вказуючи на те, що продажі зростають з часом. Тепер у нас є рівняння для продажів телефонів з плином часу:\[ A=-200e^{-0.105t}+200. \nonumber \]
Нарешті, ми можемо оцінити це,\(t = 9\) щоб знайти продажі через 9 місяців:\[ A(9)=-200e^{-0.105(9)}+200\approx 122.26\text{ thousand phones}. \nonumber \]
Обмежене зростання також зазвичай використовується для моделей навчання, оскільки, вивчаючи нову навичку, люди, як правило, спочатку швидко навчаються, потім їх швидкість вдосконалення сповільнюється, коли вони наближаються до майстерності.
Джим вивчає новий набір кодів продуктів для роботи. Кожен день він вчиться, і перевіряє своє відкликання. Припустимо, що через 4 дні Джим освоїв 70% нових кодів. Скільки часу йому знадобиться, щоб освоїти 95% кодів, якщо застосовується модель обмеженого зростання.
Рішення
У цьому випадку можлива максимальна кількість майстерності, так що\(M\) = 100%. Моделюючи його навчання\(L\), як відсоток майстерності, ми можемо написати диференціальне рівняння\(L'=k(100-L)\)
Вирішуючи, як ми це робили в попередньому прикладі, отримуємо\(L=Ae^{-kt}+100\).
Так як він почав не знати жодного з кодів\(L(0)=0\), значить\(0 = Ae^{-k(0)}+100\), так\(A = -100\).
Використовуючи це Джим освоїв 70 кодів за 4 дні\(L(4)=70\), так
\[\begin{align*} 70 = -100e^{-k(4)}+100 \\ -30 = -100e^{-k(4)} \\ 0.3 = e^{-k(4)} \\ \ln(0.3) = \ln \left(e^{-k(4)}\right) = -4k \\ k = \frac{\ln(0.3)}{-4} \approx 0.301 \end{align*}\]
Тепер у нас є рівняння\(L = -100e^{-0.301t} + 100\), ми можемо вирішити для коли\(L = 95\).
\[\begin{align*} 95 = -100e^{-0.301t}+100 \\ -5 = -100e^{-0.301t} \\ 0.05 = e^{-0.301t} \\ \ln(0.3) = \ln \left(e^{-0.301t}\right) = -0.301t \\ t = \frac{\ln(0.05)}{-0.301} \approx 9.95 \end{align*}\]
Джим досягне 95% майстерності приблизно через 10 днів.
Раніше ми використовували необмежене зростання для моделювання населення, але часто населення буде обмежено продовольством, простором та іншими ресурсами. Коли чисельність населення зростає як пропорційно її розміру, так і відносно відстані від деякого максимуму, це називається логістичним зростанням. Це призводить до диференціального рівняння\( y'=ky(M-y) \), яке є точним, але не завжди зручним у використанні. Будемо використовувати невелику модифікацію. Оскільки для розв'язання цього диференціального рівняння потрібні методи інтеграції, які ми ще не вивчили, задано форму розв'язку.
Якщо величина зростає зі швидкістю, пропорційною її розміру і відстані від максимального значення,\(M\), it can be modeled with логістичне зростання, яке має диференціальне рівняння:\[ y'=ry\left(1-\frac{y}{M}\right). \nonumber \]
\(r\)можна інтерпретувати як темпи зростання відсутніх обмежень
, тобто як зростатиме населення, якби не було максимального значення.
Це диференціальне рівняння має розв'язки виду\[ y=\frac{M}{1+Ae^{-rt}}. \nonumber \]
Колонія з 100 кроликів заноситься в меліорований ліс. Через 1 рік чисельність населення зросла до 300. За оцінками, ліс може витримати 5000 кроликів. Лісова служба планує знову ввести вовків в ліс, коли популяція кроликів досягне 3000 кроликів. Коли це станеться?
Рішення
Максимально стійке населення було дано як\(M = 5000\). Використовуючи форму рішення\[ y=\frac{M}{1+Ae^{-rt}} \nonumber \] та початкову умову,\( y(0)=100 \) ми можемо вирішити для\( A \):\[ \begin{align*} 100 & = \frac{5000}{1+Ae^{-r(0)}} &\\ 100 & = \frac{5000}{1+A} &\qquad\text{Simplify.}\\ 100(1+A) & = 5000 &\qquad\text{Multiply both sides by \( 1+A \).}\\ 1+A & = 50 &\qquad\text{Divide by 100.}\\ A & = 49 & \end{align*} \nonumber \]
Тепер, використовуючи\( y(1)=300 \), ми можемо вирішити для\(r\):\[ \begin{align*} 300 & = \frac{5000}{1+49e^{-r(1)}} \\ 300\left(1+49e^{-r}\right) & = 5000 \\ 1+49e^{-r} & = \frac{5000}{300} \\ e^{-r} & = \frac{\frac{50}{3}-1}{49}\approx 0.3197 \\ -r & = \ln(0.3197) \\ r & = -\ln(0.3197)\approx 1.1404 \end{align*} \nonumber \]
Тепер у нас є рівняння для населення через\(t\) роки:\[ y=\frac{5000}{1+49e^{-1.1404t}}. \nonumber \]
Щоб відповісти на початкове рівняння, коли популяція кроликів досягне 3000, нам потрібно вирішити,\(t\) коли\(y = 3000\):\[ \begin{align*} 3000 & = \frac{5000}{1+49e^{-1.1404t}} \\ 3000\left(1+49e^{-1.1404t}\right) & = 5000 \\ e^{-1.1404t} & = \frac{\frac{5}{3}-1}{49}\approx 0.01361 \\ t & = \frac{\ln(0.01361)}{-1.1404}\approx 3.77\text{ years}. \end{align*} \nonumber \]
Логістичне зростання також є гарною моделлю для нерекламованих продажів. Новий продукт, який не рекламується, спочатку буде повільно збільшуватися продажі, а потім рости, як сарафанне радіо поширюється і люди знайомі з продуктом. Продажі будуть вирівнюватися, коли вони наближаються до насичення ринку.
