2.6: Правило ланцюга
- Page ID
- 60392
Є ще один тип складної функції, яку ми хочемо знати, як диференціювати: склад. Правило ланцюга дозволить нам знайти похідну від композиції. (Це останнє похідне правило, яке ми дізнаємося!)
Знайдіть похідну від\( y=\left(4x^3+15x\right)^2 \).
Рішення
Це не простий многочлен, тому ми поки не можемо використовувати основні правила будівельного блоку. Це продукт, тому ми могли б написати його як\(y=\left(4x^3+15x\right)^2=\left(4x^3+15x\right)\left(4x^3+15x\right)\) і використовувати правило продукту. Або ми могли б помножити його і просто диференціювати отриманий многочлен. Я зроблю це другим способом:\[ \begin{align*} y & = \left(4x^3+15x\right)^2\\ & = 16x^6+120x^4+225x^2\\ y' & = 96x^5+480x^3+450x \end{align*} \nonumber \]
Тепер припустимо, що ми хочемо знайти похідну від\(y=\left(4x^3+15x\right)^{20}\). Ми могли б написати його як продукт з 20 факторами і використовувати правило продукту, або ми могли б помножити його. Але я не хочу цього робити, чи не так?
Потрібен більш простий спосіб, правило, яке впорається з такою композицією. Правило ланцюга трохи складне, але воно рятує нас набагато складнішою алгеброю множення чогось подібного. Він також буде обробляти композиції там, де його неможливо було б помножити.
Правило ланцюга є загальним місцем для студентів, щоб зробити помилки. Частково причина полягає в тому, що до позначення потрібно трохи звикнути. І частина причини полягає в тому, що студенти часто забувають використовувати його, коли повинні. Коли слід використовувати правило ланцюга? Майже кожен раз, коли ви берете похідну.
У чому випливає,\(f\) and \(g\) are differentiable functions where \(y = f(g(x))\). We could alternatively write \( y=f(u) \) and \( u=g(x) \).
Правило ланцюга (позначення Лейбніца)
\[\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}\nonumber \]
Зверніть увагу,\(du\) що здається скасувати. Це одна з переваг позначення Лейбніца - вона може нагадати вам про те, як правило ланцюга змикається між собою.
Правило ланцюга (з використанням простих позначень)
\[\frac{d}{dx} f\left(g(x)\right) =f'\left(g(x)\right)\cdot g'(x)\nonumber \]
Правило ланцюга (прописом)
Похідна композиції - це похідна від зовнішнього (з внутрішньою частиною залишається незмінною) TIMES похідне від внутрішньої частини.
Я декламую версію словами кожен раз, коли беру похідну, особливо якщо функція складна.
Знайдіть похідну від\( y=\left(4x^3+15x\right)^2 \).
Рішення
Це те саме, що ми робили раніше, множивши. Цього разу скористаємося Правилом ланцюга: Внутрішня функція - це те, що з'являється всередині дужок:\( 4x^3+15x \). Зовнішня функція - це перше, що ми знаходимо, коли ми входимо ззовні - це квадратна функція,\((\text{inside})^2\).
Похідна цієї зовнішньої функції є\((2\cdot\text{inside})\). Тепер, використовуючи правило ланцюга, похідна нашої початкової функції\((2\cdot\text{inside})\) TIMES - похідна внутрішньої (яка є\( 12x^2+15 \)):\[ y'=2\left(4x^3+15x\right)\left(12x^2+15 \right)\nonumber \]
Якщо помножити це, ви отримаєте ту ж відповідь, яку ми отримали раніше. Ура! Алгебра працює!
Знайдіть похідну від\( y=\left(4x^3+15x\right)^{20} \).
Рішення
Тепер у нас є спосіб впоратися з цим. Це похідне від зовнішнього TIMES похідне від внутрішньої.
Зовнішня функція є\( \left(\text{inside}\right)^{20} \), яка має похідну\( 20\left(\text{inside}\right)^{19}\), так\[y'=20\left(4x^3+15x\right)^{19}\left(12x^2+15\right).\nonumber \]
Диференціювати\( y=e^{x^2+5} \).
Рішення
Це не проста експоненціальна функція; це композиція. Типовий калькулятор або комп'ютерний синтаксис може допомогти вам побачити, що таке функція «всередині» тут. Наприклад, на калькуляторі TI, коли ви натискаєте\( e^x \) клавішу, він відкриває дужки:\(\boxed{e^{\wedge}(}\). Це говорить вам про те, що «всередині» експоненціальної функції є показником. Тут внутрішня частина - експонента\( x^2+5 \). Тепер ми можемо використовувати Правило ланцюга: Ми хочемо, щоб похідна зовнішнього TIMES була похідною від внутрішньої частини. Зовні - це щось
функція, тому її похідна - це те ж саме.\(e\) Похідне від того, що знаходиться всередині\(2x\). Так\[\frac{d}{dx}\left( e^{x^2+5} \right)= \left( e^{x^2+5} \right)\cdot (2x).\nonumber \]
Таблиця дає значення для\(f\),\(f'\)\(g\),, і\(g'\) в ряді точок. Використовуйте ці значення для визначення\(( f \circ g )(x)\) і\(( f \circ g ) '(x)\) at\(x = -1\) і 0.
| \( x \) | \( f(x) \) | \( g(x) \) | \( f'(x) \) | \( g'(x) \) | \((f\circ g)(x)\) | \((g\circ f)(x)\) |
| -1 | 2 | 3 | 1 | 0 | ||
| 0 | -1 | 1 | 3 | 2 | ||
| 1 | 1 | 0 | -1 | 3 | ||
| 2 | 3 | -1 | 0 | 1 | ||
| 3 | 0 | 2 | 2 | -1 |
Рішення
\[ \begin{align*} (f\circ g)(-1) & = f\left(g(-1)\right)=f(3)=0\\ (f\circ g)(0) & = f\left(g(0)\right)=f(1)=1\\ (f\circ g)'(-1) & = f'\left(g(-1)\right)\cdot g'(-1)=f'(3)\cdot (0)=(2)(0)=0 \text{ and}\\ (f\circ g)'(0) & = f'\left(g(0)\right)\cdot g'(0)=f'(1)\cdot (2)=(-1)(2)=-2 \end{align*} \nonumber \]
Якщо зараз у 2400 людей є захворювання, і кількість людей з хворобою, здається, подвоюється кожні 3 роки, то кількість людей, які очікують мати хворобу в\(t\) роки, становить\( y=2400\cdot 2^{t/3} \).
- У скількох людей очікується захворювання через 2 роки?
- Коли очікується, що хвороба хворіє на 50 000 людей?
- Наскільки швидко кількість людей із захворюванням, як очікується, зросте зараз і через 2 роки?
- У 2 роки\(y = 2400\cdot 2^{2/3} \approx 3,810\) людина.
- Ми знаємо\(y = 50,000\), і нам потрібно вирішити\(50,000 = 2400\cdot 2^{t/3}\) для\(t\). Ми могли б почати з виділення експоненціальної, розділивши обидві сторони на 2400.\[ \begin{align*} \frac{50000}{2400} & = 2^{t/3} \\ \ln\left(\frac{50000}{2400}\right) & = \ln\left(2^{t/3}\right) \qquad \text{(Taking the natural log of both sides.)}\\ \ln\left(\frac{50000}{2400}\right) & = \frac{t}{3}\ln(2) \qquad \text{(Using the exponent property for logs.)}\\ t & = \frac{3\ln\left(\frac{50000}{2400}\right)}{\ln(2)}\approx 13.14\text{ years}\qquad \text{(Solving for \( t \).)} \end{align*} \nonumber \] Ми очікуємо, що 50,000 людей матимуть хворобу приблизно через 13.14 років.
- Це просять,\(\frac{dy}{dt}\) коли\(t =\) 0 і 2 роки. Використовуючи правило ланцюга,\[ \begin{align*} \frac{dy}{dt} & = \frac{d}{dt}\left(2400\cdot 2^{t/3}\right) \\ & = 2400\cdot 2^{t/3}\cdot \ln(2)\cdot\frac{1}{3} \\ & \approx 554.5\cdot 2^{t/3} \end{align*} \nonumber \] Отже,\( t=0 \) за темпами зростання захворювання становить приблизно\(554.5\cdot 2^0 \approx 554.5\) людей/рік. Через 2 роки темпи зростання становитимуть приблизно\(554.5\cdot 2^{2/3} \approx 880\) людини/рік.
Похідні складних функцій
Тепер ви готові взяти похідну від деяких могутніх складних функцій. Але як сказати, яке правило застосовується в першу чергу? Пропрацюйте свій шлях ззовні - з чим ви стикаєтеся в першу чергу? Це перше правило, яке вам потрібно. Використовуйте правила продукту, частки та ланцюга, щоб знімати шари по одному, поки ви не опинитеся всередині.
Знайти\( \frac{d}{dx}\left( e^{3x}\cdot\ln(5x+7) \right) \).
Рішення
Зайшовши ззовні, ми бачимо, що це добуток двох (складних) функцій. Отже, спочатку нам знадобиться Правило продукту. Ми заповнимо відомі нам шматки, а потім зможемо визначити решту як окремі кроки і замінити в кінці:\[\frac{d}{dx}\left( e^{3x}\cdot\ln(5x+7) \right)=\left( \frac{d}{dx}\left( e^{3x}\right)\right)\cdot\ln(5x+7)+ e^{3x}\cdot \left(\frac{d}{dx}\left(\ln(5x+7) \right)\right)\nonumber \]
Тепер в якості окремих кроків знайдемо\[\frac{d}{dx}\left( e^{3x}\right)=3e^{3x} \quad \text{ (using the Chain Rule)}\nonumber \] і\[\frac{d}{dx}\left(\ln(5x+7) \right)=\frac{1}{5x+7}\cdot 5 \quad \text{ (also using the Chain Rule)}.\nonumber \]
Нарешті, щоб замінити їх на свої місця:\[\frac{d}{dx}\left( e^{3x}\cdot\ln(5x+7) \right)=\left( 3e^{3x}\right)\cdot\ln(5x+7)+ e^{3x}\cdot \left(\frac{1}{5x+7}\cdot 5\right)\nonumber \]
(Ми можемо зупинитися на цьому — нам не потрібно намагатися спростити далі.)
Диференціювати\( z=\left(\dfrac{3t^3}{e^t(t-1)}\right)^4 \).
Рішення
Не панікуйте! Коли ми входимо ззовні, що перше, з чим ми стикаємося? Це та четверта влада. Це говорить нам про те, що це композиція, (складна) функція, піднята до четвертої влади.
Крок перший: Використовуйте правило ланцюга. Похідна від зовнішнього TIMES похідна від внутрішньої:\[\frac{dz}{dt}=\frac{d}{dt}\left(\frac{3t^3}{e^t(t-1)}\right)^4=4\left(\frac{3t^3}{e^t(t-1)}\right)^3\cdot \frac{d}{dt}\left(\frac{3t^3}{e^t(t-1)}\right)\nonumber \]
Тепер ми один крок всередині, і ми можемо зосередитися тільки на\( \frac{d}{dt}\left(\frac{3t^3}{e^t(t-1)}\right) \) частині. Тепер, коли ви входите ззовні, перше, що ви стикаєтеся, це частка - це частка двох (складних) функцій.
Крок другий: Використовуйте правило частки. Похідна чисельника проста, тому ми можемо просто обчислити її. Похідна від знаменника трохи складніше, тому залишимо її поки що:\[ \frac{d}{dt}\left(\frac{3t^3}{e^t(t-1)}\right)=\frac{\left( 9t^2 \right)\left( e^t(t-1) \right)-\left( 3t^3 \right)\left( \frac{d}{dt}\left( e^t(t-1) \right) \right)}{\left(e^t(t-1)\right)^2} \nonumber \]
Тепер ми пройшли ще один крок всередині, і ми можемо сконцентруватися тільки на\( \frac{d}{dt}\left( e^t(t-1) \right) \) частині, яка включає в себе продукт.
Крок третій: Використовуйте правило продукту:\[ \frac{d}{dt}\left( e^t(t-1)\right) = \left( e^t \right)(t-1)+\left( e^t \right)(1)\nonumber \]
І тепер ми весь шлях в - більше ніяких похідних, щоб взяти!
Крок четвертий: Тепер це лише питання заміни назад — будьте обережні зараз!
\[ \frac{d}{dt}\left( e^t(t-1)\right) = \left( e^t \right)(t-1)+\left( e^t \right)(1) \nonumber \]\[ \frac{d}{dt}\left(\frac{3t^3}{e^t(t-1)}\right)=\frac{\left( 9t^2 \right)\left( e^t(t-1) \right)-\left( 3t^3 \right)\left( \left( e^t \right)(t-1)+\left( e^t \right)(1) \right)}{\left(e^t(t-1)\right)^2} \nonumber \]так\[\frac{dz}{dt}=\frac{d}{dt}\left(\frac{3t^3}{e^t(t-1)}\right)^4=4\left(\frac{3t^3}{e^t(t-1)}\right)^3\cdot \left( \frac{\left( 9t^2 \right)\left( e^t(t-1) \right)-\left( 3t^3 \right)\left( \left( e^t \right)(t-1)+\left( e^t \right)(1) \right)}{\left(e^t(t-1)\right)^2} \right)\nonumber \]
Фу!
Що робити, якщо похідної не існує?
Функція називається диференційованою в точці, якщо її похідна існує в цій точці.
Ми діяли так, ніби похідні існують скрізь для кожної функції. Це вірно для більшості функцій, з якими ви зіткнетеся в цьому класі. Але є деякі загальні місця, де похідної не існує.
Пам'ятайте, що похідна - це нахил дотичної лінії до кривої. Ось про що потрібно подумати.
Де може не існувати схилу? Якщо дотична лінія вертикальна, похідної не існуватиме.
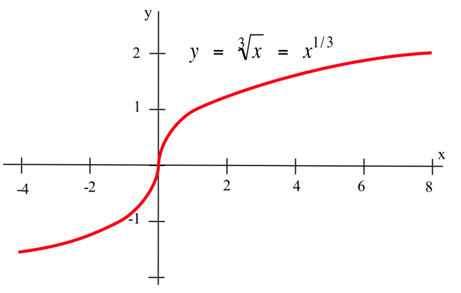
Показати,\( f(x)=\sqrt[3]{x}=x^{1/3} \) що не диференціюється в\(x = 0\).
Рішення
Знаходження похідної,\( f(x)=\frac{1}{3}x^{-2/3}=\frac{1}{3x^{2/3}} \). В\(x = 0\), ця функція не визначена. З графіка ми бачимо, що дотична лінія до цієї кривої на\(x = 0\) вертикальній з невизначеною нахилом, тому похідна не існує при\(x = 0\).
Де може не існувати дотичної лінії?
Якщо на графіку є гострий кут (cusp), похідна не буде існувати в цій точці, оскільки немає чітко визначеної дотичної лінії (дотичної, якщо хочете).
Якщо на графіку є розрив (стрибок, перерва, дірка на графіку або вертикальна асимптота), дотична лінія буде різною з обох боків, і похідна не буде існувати в цій точці.
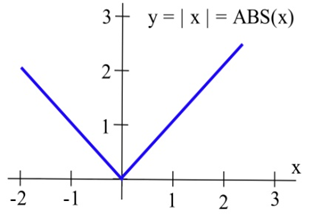
Показати,\( f(x)=|x| \) що не диференціюється в\(x = 0\).
Рішення
У лівій частині графіка нахил прямої дорівнює -1. У правій частині графіка нахил дорівнює +1. У гострому куті немає чітко визначеної дотичної лінії\(x = 0\), тому функція не диференційована в цій точці.