2.5: Правило ланцюга

Ми розглянули майже всі похідні правила, які стосуються комбінацій двох (або більше) функцій. Операції додавання, віднімання, множення (у тому числі на константу) та ділення призвели до правил суми та різниці, правила постійного множинного, силового правила, правила продукту та правила частки. Щоб завершити список правил диференціації, розглянемо останній спосіб об'єднання двох (або більше) функцій: процес композиції (тобто одна функція «всередині» іншої).

Одним із прикладів композиції функцій є$f(x) = \cos(x^2)$. Ми в даний час не знаємо, як обчислити цю похідну. Якщо змушені здогадатися, можна було б, швидше за все$f^\prime(x) = -\sin(2x)$, здогадатися, де ми$-\sin x$ визнаємо похідною від$\cos x$ і$2x$ як похідну від$x^2$. Однак це не так;$f^\prime(x)\neq -\sin(2x)$. У прикладі 62 ми побачимо правильну відповідь, яка використовує нове правило, яке вводить цей розділ, правило ланцюга.

Перш ніж визначити це нове правило, згадайте позначення для композиції функцій. Ми пишемо$(f \circ g)(x)$ або$f(g(x))$, читаємо як "$f$$g$of»$x$, щоб позначити композицію$f$ с$g$. У стенографії ми просто пишемо$f \circ g$ або$f(g)$ і читаємо як «$f$з»$g$. Перш ніж дати відповідне правило диференціації, ми зауважимо, що правило поширюється на кілька композицій$f(g(h(j(x))))$, таких як$f(g(h(x)))$ або тощо.

Щоб мотивувати правило, давайте розглянемо три похідні, які ми вже можемо обчислити.

Приклад 59: Вивчення подібних похідних

Знайдіть похідні від

1. $F_1(x) = (1-x)^2$,
2. $F_2(x) = (1-x)^3,$і
3. $F_3(x) = (1-x)^4.$

Пізніше ми побачимо, чому ми використовуємо індекси для різних функцій і в верхньому регістрі$F$.

Рішення

Для того, щоб використовувати правила, які ми вже маємо, ми повинні спочатку розширити кожну функцію як

1. $F_1(x) = 1 - 2x + x^2$,
2. $F_2(x) = 1 - 3x + 3x^2 - x^3$і
3. $F_3(x) = 1 - 4x + 6x^2 - 4x^3 + x^4$.

Не важко помітити, що:

$$\begin{align*} F_1^\prime(x) &= -2 + 2x \\[4pt] F_2^\prime(x) &= -3 + 6x - 3x^2 \\[4pt] F_3^\prime (x) &= -4 + 12x - 12x^2 + 4x^3. \end{align*}$$

Цікавим фактом є те, що їх можна переписати як

$$F_1^\prime (x) = -2(1-x),\quad F_2^\prime(x) = -3(1-x)^2 \text{ and }F_3^\prime (x) = -4(1-x)^3.$$

Візерунок може вискочити на вас. Визнайте, що кожна з цих функцій є складом, дозволяючи$g(x) = 1-x$:

$$\begin{eqnarray*}F_1(x) = f_1(g(x)),& \text{ where } f_1(x) = x^2,\\ F_2(x) = f_2(g(x)),& \text{ where } f_2(x) = x^3,\\ F_3(x) = f_3(g(x)),& \text{ where } f_3(x) = x^4. \end{eqnarray*}$$

Ми повернемося до цього прикладу після надання формальних заяв Правило ланцюга; на даний момент ми просто ілюструємо шаблон.

Теорема 18: Правило ланцюга

$y = f(u)$Дозволяти диференційовні функції$u$ і$u = g(x)$ нехай диференційовна функція$x$. Тоді$y=f(g(x))$ є диференційованою функцією$x$, і $$y^\prime = f^\prime(g(x))\cdot g^\prime(x).$$

Щоб допомогти зрозуміти правило ланцюга, повернемося до Прикладу 59.

Приклад 60: Використання правила ланцюга

Використовуйте Правило ланцюга, щоб знайти похідні наступних функцій, як наведено в прикладі 59.

Рішення

Приклад 59 закінчився визнанням того, що кожна з заданих функцій насправді була складом функцій. Щоб уникнути плутанини, ми ігноруємо більшість індексів тут.

$F_1(x) = (1-x)^2$:

Ми виявили, що $$y=(1-x)^2 = f(g(x)), \text{ where } f(x) = x^2\ \text{ and }\ g(x) = 1-x.$$

Щоб знайти$y^\prime$, застосовуємо Правило ланцюга. Нам потрібно$f^\prime(x)=2x$ і$g^\prime(x)=-1.$

Частина правила ланцюга використовує$f^\prime(g(x))$. Це означає заміну$g(x)$$x$ в рівнянні для$f^\prime(x)$. Тобто,$f^\prime(x) = 2(1-x)$. Закінчивши правило ланцюга, яке ми маємо $$y^\prime = f^\prime(g(x))\cdot g^\prime(x) = 2(1-x)\cdot (-1) = -2(1-x)= 2x-2.$$

$F_2(x) = (1-x)^3$:

Нехай$y = (1-x)^3 = f(g(x))$, де$f(x) = x^3$ і$g(x) = (1-x)$. У нас є$f^\prime(x) = 3x^2$, так$f^\prime(g(x)) = 3(1-x)^2$. Правило ланцюга потім стверджує $$y^\prime = f^\prime(g(x))\cdot g^\prime (x) = 3(1-x)^2\cdot(-1) = -3(1-x)^2.$$

$F_3(x) = (1-x)^4$:

Нарешті, коли$y = (1-x)^4$, у нас є$f(x)= x^4$ і$g(x) = (1-x)$. Таким чином$f^\prime(x) = 4x^3$ і$f^\prime(g(x)) = 4(1-x)^3$. Таким чином $$y^\prime = f^\prime(g(x))\cdot g^\prime(x) = 4(1-x)^3\cdot (-1) = -4(1-x)^3.$$

Приклад 60 продемонстрував певну закономірність: коли$f(x)=x^n$, то$y^\prime =n\cdot (g(x))^{n-1}\cdot g^\prime (x)$. Це називається Узагальненим правилом влади.

Теорема 19: Узагальнене правило потужності

$g(x)$Дозволяти диференційовні функції і нехай$n\neq 0$ бути цілим числом. Тоді $$\dfrac{d}{dx}\Big(g(x)^n\Big) = n\cdot \big(g(x)\big)^{n-1}\cdot g^\prime (x).$$

Це дозволяє нам швидко знайти похідну від функцій на кшталт$y = (3x^2-5x+7+\sin x)^{20}$. Хоча це може виглядати залякуючим, Узагальнене правило влади стверджує, що $$y^\prime = 20(3x^2-5x+7+\sin x)^{19}\cdot (6x-5+\cos x).$$

Ставтеся до похідного процесу крок за кроком. У щойно наданому прикладі спочатку помножте на 20, потім перепишіть внутрішню частину дужок, піднімаючи все це до$^{\text{th}}$ потужності 19. Потім подумайте про похідну виразу всередині дужок і помножте на це.

Тепер ми розглянемо більше прикладів, які використовують правило ланцюга.

Приклад 61: Використання правила ланцюга

Знайдіть похідні наступних функцій:

1. $y = \sin{2x}$
2. $y= \ln (4x^3-2x^2)$
3. $y = e^{-x^2}$

Рішення

1. Розглянемо$y = \sin 2x$. Визнайте, що це склад функцій, де$f(x) = \sin x$ і$g(x) = 2x$. Таким чином $$y^\prime = f^\prime(g(x))\cdot g^\prime(x) = \cos (2x)\cdot 2 = 2\cos 2x.$$
2. Визнайте, що$y = \ln (4x^3-2x^2)$ це склад$f(x) = \ln x$ і$g(x) = 4x^3-2x^2$. Крім того, нагадаємо, що $$\dfrac{d}{dx}\Big(\ln x\Big) = \dfrac{1}{x}.$$ Це призводить нас до: $$y^\prime = \dfrac{1}{4x^3-2x^2} \cdot (12x^2-4x) = \dfrac{12x^2-4x}{4x^3-2x^2}= \dfrac{4x(3x-1)}{2x(2x^2-x)} = \dfrac{2(3x-1)}{2x^2-x}.$$
3. Визнайте, що$y = e^{-x^2}$ це склад$f(x) = e^x$ і$g(x) = -x^2$. Пам'ятаючи про це$f^\prime(x) = e^x$, ми маємо $$y^\prime = e^{-x^2}\cdot (-2x) = (-2x)e^{-x^2}.$$

Приклад 62: Використання правила ланцюга для пошуку дотичної лінії

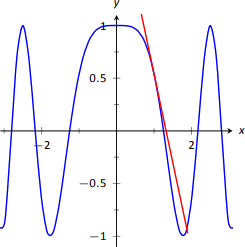
Нехай$f(x) = \cos x^2$. Знайти рівняння прямої дотичної до графіка$f$ at$x=1$.

Рішення

Дотична лінія проходить через точку$(1,f(1)) \approx (1,0.54)$ з нахилом$f^\prime(1)$. Щоб знайти$f^\prime$, нам знадобиться Правило ланцюга.

$f^\prime(x) = -\sin(x^2) \cdot(2x) = -2x\sin x^2$. Оцінений на$x=1$, у нас є$f^\prime(1) = -2\sin 1\approx -1.68$. Таким чином, рівняння дотичної прямої $$y = -1.68(x-1)+0.54 .$$

Дотична лінія начерчується разом з$f$ малюнком 2.17.

Малюнок 2.17:$f(x)=\cos x^2$ ескіз разом з його дотичною лінією в$x=1$.

Правило ланцюга використовується часто при прийомі похідних. Через це можна ознайомитися з основним процесом і вивчити закономірності, які полегшують пошук похідних швидко. Наприклад, $$\dfrac{d}{dx}\Big(\ln (\text{anything})\Big) = \dfrac{1}{\text{anything}}\cdot (\text{anything})^\prime = \dfrac{(\text{anything})^\prime}{\text{anything}}.$$

Конкретним прикладом цього є $$\dfrac{d}{dx}\Big(\ln(3x^{15}-\cos x+e^x)\Big) = \dfrac{45x^{14}+\sin x+e^x}{3x^{15}-\cos x+e^x}.$$ Хоча похідна спочатку може виглядати страхітливою, шукайте шаблон. Знаменник такий же, як і те, що було всередині природної функції журналу; чисельник - це просто його похідна.

Цей процес розпізнавання образів може бути застосований до багатьох функцій. Загалом, замість того, щоб писати «що-небудь», ми використовуємо$u$ як загальну функцію$x$. Ми тоді говоримо $$\dfrac{d}{dx}\Big(\ln u\Big) = \dfrac{u^\prime}{u}.$$

Нижче наведено короткий список того, як правило ланцюга можна швидко застосувати до звичних функцій.

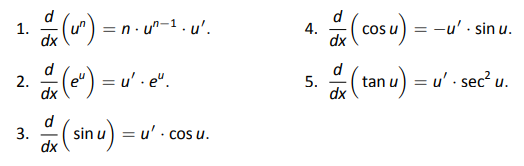
Звичайно, правило ланцюга може застосовуватися спільно з будь-яким з інших правил, які ми вже вивчили. Ми практикуємо це далі.

Приклад 63: Використання правил продукту, коефіцієнта та ланцюга

Знайдіть похідні наступних функцій.

1. $f(x) = x^5 \sin{2x^3}$
2. $f(x) = \dfrac{5x^3}{e^{-x^2}}$.

Рішення

1. Ми повинні використовувати Правила продукту та ланцюга. Не думайте, що ви повинні бути в змозі «побачити» всю відповідь негайно; швидше, просто продовжуйте крок за кроком. $$f^\prime(x) = x^5\big(6x^2\cos 2x^3\big) + 5x^4\big(\sin 2x^3\big)= 6x^7\cos2x^3+5x^4\sin 2x^3.$$
2. Ми повинні використовувати правило частки разом з правилом ланцюга. Знову ж таки, дійте поетапно. $$\begin{align*} f^\prime(x) = \dfrac{e^{-x^2}\big(15x^2\big) - 5x^3\big((-2x)e^{-x^2}\big)}{\big(e^{-x^2}\big)^2} &=\dfrac{e^{-x^2}\big(10x^4+15x^2\big)}{e^{-2x^2}}\\ &= e^{x^2}\big(10x^4+15x^2\big). \end{align*}$$

Ключ до правильної роботи цих проблем полягає в тому, щоб розбити проблему на менші, більш керовані частини. Наприклад, при спільному використанні Правил продукту та ланцюжка, просто спочатку розгляньте першу частину Правил продукту:$f(x)g^\prime(x)$. Просто перепишіть$f(x)$, потім знайдіть$g^\prime(x)$. Потім переходимо до$f^\prime(x)g(x)$ деталі. Не намагайтеся з'ясувати обидві частини відразу.

Так само, використовуючи правило частки, підійдіть до чисельника в два кроки і обробляйте знаменник після завершення цього. Тільки спростити потім.

Ми також можемо використовувати саме правило ланцюга кілька разів, як показано в наступному прикладі.

Приклад 64: Використання правила ланцюга кілька разів

Знайдіть похідну від$y = \tan^5(6x^3-7x)$.

Рішення

Визнайте, що у нас є$g(x)=\tan(6x^3-7x)$ функція «всередині»$f(x)=x^5$ функції; тобто ми маємо$y = \big(\tan(6x^3-7x)\big)^5$. Ми починаємо використовувати узагальнене правило потужності; на цьому першому кроці ми не повністю обчислюємо похідну. Швидше, ми наближаємося до цього кроку за кроком.

$$y^\prime = 5\big(\tan(6x^3-7x)\big)^4\cdot g^\prime(x).$$

Ми зараз знаходимо$g^\prime(x)$. Нам знову потрібно правило ланцюга; $$g^\prime(x) = \sec^2(6x^3-7x)\cdot(18x^2-7).$$ Поєднайте це з тим, що ми знайшли вище, щоб дати

$$\begin{align*} y^\prime &= 5\big(\tan(6x^3-7x)\big)^4\cdot\sec^2(6x^3-7x)\cdot(18x^2-7)\\ &= (90x^2-35)\sec^2(6x^3-7x)\tan^4(6x^3-7x). \end{align*}$$

Ця функція є відверто смішною функцією, що не володіє ніяким реальним практичним значенням. Графік дуже важко, оскільки функція дотичної має багато вертикальних асимптотів і$6x^3-7x$ зростає так швидко. З цього важливо дізнатися, що похідну можна знайти. Насправді це не «важко»; потрібно зробити кілька простих кроків і бути обережним, щоб стежити за тим, як застосовувати кожен з цих кроків.

Це традиційна математична вправа для пошуку похідних довільно складних функцій лише для того, щоб продемонструвати, що це можна зробити. Просто розбийте все на більш дрібні шматочки.

Приклад 65: Використання правил продукту, коефіцієнта та ланцюга

Знайдіть похідну від$f(x) = \dfrac{x\cos(x^{-2})-\sin^2(e^{4x})}{\ln(x^2+5x^4)}.$

Рішення

Ця функція, ймовірно, не має практичного застосування поза демонстрацією похідних навичок. Відповідь наведено нижче без спрощення. Він тричі використовує правило частки, правило продукту та правило ланцюга.

$$f^\prime(x) = \dfrac{\Big(\ln(x^2+5x^4)\Big)\cdot\Big[\big(x\cdot(-\sin(x^{-2}))\cdot(-2x^{-3})+1\cdot \cos(x^{-2})\big)-2\sin(e^{4x})\cdot\cos(e^{4x})\cdot(4e^{4x})\Big]-\Big(x\cos(x^{-2})-\sin^2(e^{4x})\Big)\cdot\dfrac{2x+20x^3}{x^2+5x^4}}{\big(\ln(x^2+5x^4)\big)^2}.$$

Читачеві настійно рекомендується подивитися на кожен термін і визнати, чому він там. (Тобто використовується правило частки; в чисельнику визначте термін «LodHi» і т.д.) Цей приклад демонструє, що похідні можуть обчислюватися систематично, незалежно від того, наскільки довільно складною є функція.

Правило ланцюга також має теоретичне значення. Тобто його можна використовувати для пошуку похідних функцій, які ми ще не вивчили, як це робимо в наступному прикладі.

Приклад 66: Правило ланцюга та експоненціальні функції

Використовуйте Правило ланцюга, щоб знайти похідну від$y= a^x$ де$a>0$,$a\neq 1$ є постійною.

Рішення

Ми знаємо лише, як знайти похідну від однієї експоненціальної функції:$y = e^x$; ця задача просить нас знайти похідну від функцій, таких як$y = 2^x$.

Це може бути досягнуто шляхом рерайтингу$a^x$ в плані$e$. Згадуючи, що$e^x$ і$\ln x$ є зворотними функціями, ми можемо написати

$$a = e^{\ln a} \quad \text{and so } \quad y = a^x = e^{\ln (a^x)}. \nonumber$$

За властивістю експоненти логарифмів ми можемо «збити» силу, щоб отримати

$$y = a^x = e^{x (\ln a)}. \nonumber$$

Функція тепер композиція$y=f(g(x))$, з$f(x) = e^x$ і$g(x) = x(\ln a)$. Так як$f^\prime(x) = e^x$ і$g^\prime(x) = \ln a$, правило ланцюга дає

$$y^\prime = e^{x (\ln a)} \cdot \ln a. \nonumber$$

Нагадаємо, що$e^{x(\ln a)}$ термін на правій стороні якраз$a^x$, наша оригінальна функція. Таким чином, похідна містить саму вихідну функцію. У нас є

$$y^\prime = y \cdot \ln a = a^x\cdot \ln a. \nonumber$$

Правило ланцюга в поєднанні з похідним правилом$e^x$ дозволяє знайти похідні всіх експоненціальних функцій.

Попередній приклад дав результат, гідний власної «коробки».

Теорема 20: Похідні експоненціальних функцій

Нехай$f(x)=a^x$, для$a>0, a\neq 1$. Потім$f$ диференціюється для всіх дійсних чисел і

$$f^\prime(x) = \ln a\cdot a^x. \nonumber$$

Альтернативні позначення правила ланцюга

Повчально зрозуміти, як виглядає «Правило ланцюга», використовуючи$\dfrac{dy}{dx}$ "" позначення замість$y^\prime$ позначення. Припустимо, що$y=f(u)$ є функцією$u$, де$u=g(x)$ є функція$x$, як зазначено в теоремі 18. Потім, через композицію$f \circ g$, ми можемо думати про функції$x$, як$y=f(g(x))$.$y$ Таким чином,$y$ похідна щодо має$x$ сенс; ми можемо говорити про$\dfrac{dy}{dx}.$ це призводить до цікавого прогресування позначення:

\[\begin{align*}y^\prime &= f^\prime(g(x))\cdot g^\prime(x) \\ \dfrac{dy}{dx} &= y^\prime(u) \cdot u^\prime(x)\quad \text{(since $y=f(u)$ and $u=g(x)$)}\\ \dfrac{dy}{dx} &= \dfrac{dy}{du} \cdot \dfrac{du}{dx}\quad \text{(using "fractional'' notation for the derivative)}\end{align*}\]

Тут виділяється «дробовий» аспект похідного позначення. З правого боку, здається, що "$du$" умови скасовують, залишаючи $$\dfrac{dy}{dx} = \dfrac{dy}{dx}.$$

Важливо усвідомлювати, що ми не скасовуємо ці терміни; похідне позначення$\dfrac{dy}{dx}$ є одним символом. Не менш важливо усвідомлювати, що дане позначення було обрано саме через таку поведінку. Це полегшує застосування правила ланцюга з декількома змінними. Наприклад,

$$\dfrac{dy}{dt} = \dfrac{dy}{d\bigcirc} \cdot \dfrac{d\bigcirc}{d\triangle} \cdot \dfrac{d\triangle}{dt}.$$

де$\bigcirc$ і$\triangle$ є будь-якими змінними, які ви хотіли б використовувати.

Одним з найпоширеніших способів «візуалізації» Правила ланцюга є розгляд набору зубчастих коліс, як показано на малюнку 2.18. Зуби шестерні мають 36, 18 і 6 зубів відповідно. Це означає, що за кожен оборот$x$ шестерні$u$ шестерня обертається двічі. Тобто швидкість, з якою$u$ шестерня робить оборот, в два рази швидше швидкості, з якою$x$ шестерня робить оборот. Використовуючи термінологію числення, швидкість$u$ -зміни, щодо$x$, є$\dfrac{du}{dx} = 2$.

Малюнок 2.18: Серія передач для демонстрації правила ланцюга. Зверніть увагу, як$\dfrac{dy}{dx}=\dfrac{dy}{du}\cdot\dfrac{du}{dx}$.

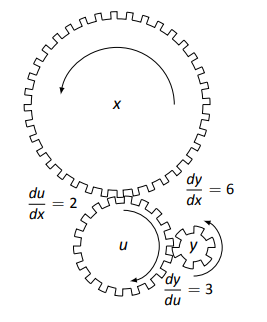
Так само кожна революція$u$ викликає 3 обороти$y$:$\dfrac{dy}{du} = 3$. Як$y$ змінюється стосовно$x$? За кожну революцію$x$,$y$ обертається 6 разів; тобто, $$\dfrac{dy}{dx} = \dfrac{dy}{du}\cdot \dfrac{du}{dx} = 2\cdot 3 = 6.$$

Потім ми можемо розширити правило ланцюга з більшою кількістю змінних, додавши більше передач до зображення.

Важко переоцінити важливість правила ланцюга. Так часто функції, які ми маємо справу з склади двох або більше функцій, що вимагають від нас використовувати це правило для обчислення похідних. Він часто використовується на практиці, коли фактичні функції невідомі. Швидше за допомогою вимірювання ми можемо обчислити$\dfrac{dy}{du}$ і$\dfrac{du}{dx}$. З нашим знанням правила ланцюга знайти$\dfrac{dy}{dx}$ просто.

У наступному розділі ми використовуємо Правило ланцюга для обґрунтування іншої техніки диференціації. Є багато кривих, які ми можемо намалювати в площині, які провалили «тест вертикальної лінії». Наприклад, розглянемо$x^2+y^2=1$, який описує одиницю кола. Нам все ще може бути цікаво знайти нахили дотичних ліній до кола в різних точках. Наступний розділ показує, як ми можемо знайти$\dfrac{dy}{dx}$ без попереднього «рішення для»$y$. Хоча ми можемо в цьому випадку, в багатьох інших випадках рішення для$y$ неможливо. У цих ситуаціях неявна диференціація незамінна.