2.1: Прелюдія до похідної

Last updated
Save as PDF

Page ID: 60366

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Ідея пречислення: нахил і швидкість зміни

Нахил лінії вимірює, наскільки швидко лінія піднімається або падає, коли ми рухаємося зліва направо вздовж лінії. Він вимірює швидкість зміни y-координати щодо змін координати x. Якщо лінія представляє відстань, пройдену в часі, наприклад, то її нахил представляє швидкість. На малюнку можна нагадати собі, як ми розраховуємо ухил, використовуючи дві точки на лінії:

схил — \( m=\text{Slope from \( P \)до\( Q \)} =\ dfrac {\ текст {підйом}} {\ текст {запустити}} =\ dfrac {y_2-y_1} {x_2-x_1} =\ dfrac {\ Дельта у} {\ Дельта х}\)

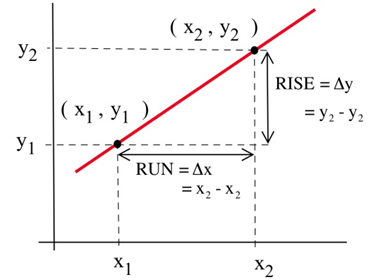
Ми хотіли б мати можливість отримати таку ж інформацію (як швидко крива піднімається або падає, швидкість з відстані), навіть якщо графік не є прямою лінією. Але що станеться, якщо ми спробуємо знайти нахил кривої, як на малюнку нижче?

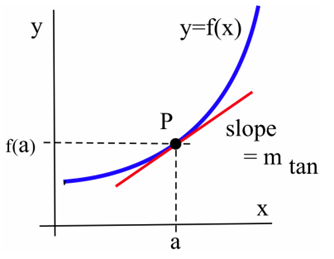
Нам потрібні дві точки для того, щоб визначити нахил лінії. Як ми можемо знайти нахил кривої лише в одній точці? Відповідь, як запропоновано на малюнку, полягає в тому, щоб знайти нахил дотичної лінії до кривої в цій точці. Більшість з нас мають інтуїтивне уявлення про те, що таке дотична лінія. На жаль, «дотичну лінію» важко точно визначити.

Визначення: Січна лінія

Січна лінія - це лінія між двома точками на кривій.

Дивіться зображення нижче:

Не можу зовсім зробити це ще визначення: дотична лінія

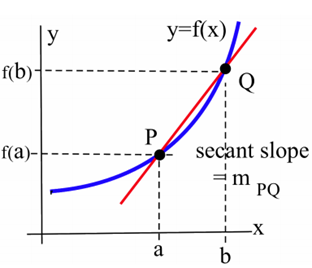
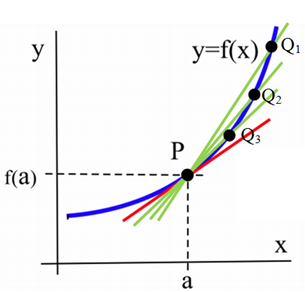
Дотична лінія - це лінія в одній точці кривої... що робить все можливе, щоб бути кривою в цій точці?

Як ви можете бачити на зображенні нижче, чим ближче точка до точки\(Q\), тим ближче\(P\) січний нахил потрапляє до дотичного нахилу. Це буде ключовим для знаходження дотичного нахилу, але спочатку нам потрібно більш ретельно визначити ідею наближення до.