2.1: Односторонні типи обмежень
- Page ID
- 54353
Односторонній межа - це саме те, що ви могли б очікувати; межа функції, оскільки вона наближається до певного значення x з правого або лівого боку. Односторонні межі допомагають розібратися з проблемою розриву стрибка і двох сторін не збігаються.
Чи є наступна кускова функція безперервна?
\ [f (x) =\ ліворуч\ {\ begin {масив} {cc}
-x-2 & x<1\\
-3 & x = 1\\
x^ {2} -4 & 1<x
\ end {масив}\ праворуч.\]
Оцінка односторонніх обмежень та безперервності
Односторонній ліміт може бути оцінений як зліва, так і справа. Оскільки ліве і праве не є абсолютними напрямками, більш точний спосіб мислення про напрямок - «з негативного боку» або «з позитивної сторони». Позначення для цих односторонніх меж:
\[\lim _{x \rightarrow a^{-}} f(x)\]
і
\[\lim _{x \rightarrow a^{+}} f(x)\]
Негативний у верхньому рядку a не є показником. Замість цього він вказує з негативного боку. Так само позитивний верхній індекс не є показником, це просто означає з позитивної сторони. При оцінці односторонніх меж не має значення, що функція робить у фактичній точці або що функція робить на іншій стороні числа. Ваше завдання полягає в тому, щоб визначити, яка висота функції повинна бути, використовуючи тільки докази з одного боку.
Візьміть графік нижче. Які односторонні межі при -5, -1, 3 і 5?
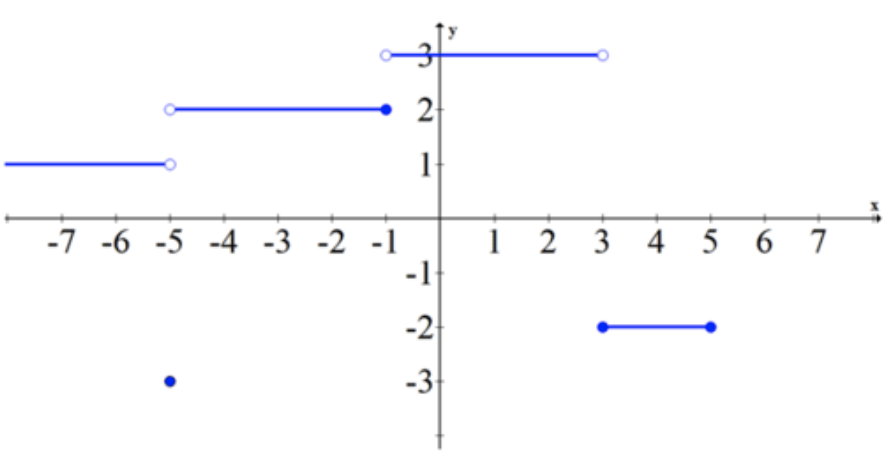
Фонд CK-12 - CCSA
Кожна точка повинна мати дві межі, один зліва і один справа.
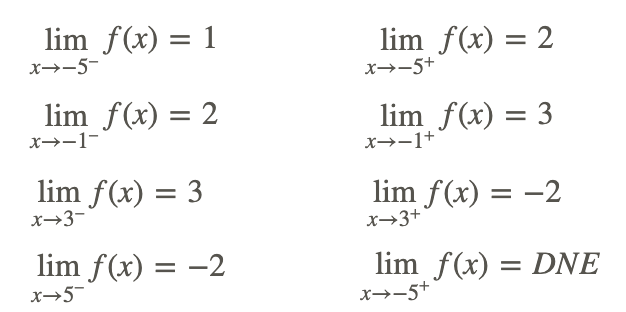
Ви визначили безперервність у минулому як здатність малювати функцію повністю, не знімаючи олівець з паперу. Тепер ви можете визначити більш суворе визначення безперервності.
Безперервність у точці існує, коли ліві та праві межі збігаються з функцією, оціненою в цій точці. Іншими словами, функція є безперервною при a if:
\[\lim _{x \rightarrow a^{-}} f(x)=f(a)=\lim _{x \rightarrow a^{+}} f(x)\]
Щоб ціла функція була безперервною, функція повинна бути безперервною в кожній точці нерозривної області.
Приклади
Приклад 1
Раніше вас запитали, як підтвердити функцію
\ [f (x) =\ ліворуч\ {\ begin {масив} {cc}
-x-2 & x<1\\
-3 & x = 1\\
x^ {2} -4 & 1<x
\ end {масив}\ праворуч.\]
є безперервним. Для того, щоб підтвердити або спростувати, що функція є безперервною, графічні інструменти недостатньо точні. Іноді розриви стрибка можуть бути відключені настільки невеликою кількістю, що пікселі на дисплеї вашого калькулятора не будуть відображати різниці. Ваш калькулятор, безумовно, не відображатиме знімні розриви.
Слід зазначити, що на графіку все зліва від 1 є безперервним, оскільки це просто лінія. Далі слід зазначити, що все праворуч від 1 також безперервно з тієї ж причини. Єдиний момент, який потрібно перевірити, - це x = 1. Щоб перевірити безперервність, явно використовуйте визначення та оцініть всі три частини, щоб побачити, чи рівні вони.
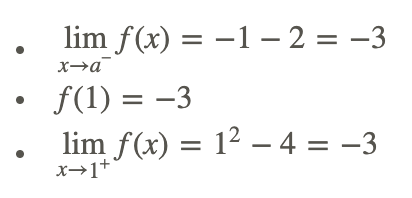
Тому,
\[\lim _{x \rightarrow 1^{-}} f(x)=f(1)=\lim _{x \rightarrow 1^{+}} f(x)\]
і функція безперервна при x = 1 і скрізь.
Приклад 2
Оцініть односторонню межу на 4 від негативного напрямку чисельно.
\[f(x)=\frac{x^{2}-7 x+12}{x-4}\]
Пам'ятайте, що оцінка чисельно означає, що ви повинні використовувати таблицю. При створенні таблиці використовуйте тільки значення, які менше 4.
| х | 3.9 | 3.99 | 3.999 |
| f (х) | 0.9 | 0,99 | 0.999 |
\[\lim _{x \rightarrow 4^{-}}\left(\frac{x^{2}-7 x+12}{x-4}\right)=1\]
Приклад 3
Оцініть наступні межі.
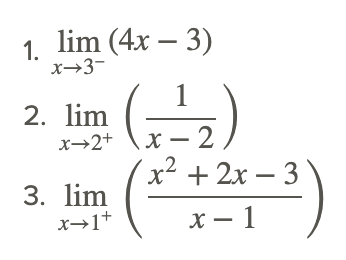
Більшу частину часу односторонні межі такі ж, як і відповідна двостороння межа. Винятки становлять випадки, коли є розриви стрибків, які зазвичай трапляються лише з кусковими функціями, та нескінченні розриви, які зазвичай трапляються лише з раціональними функціями.
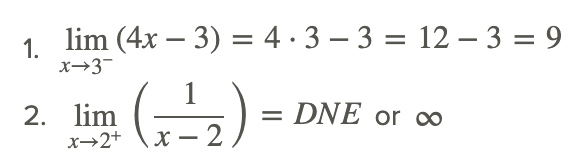
Причина, чому ∞ є кращим у цьому випадку, полягає в тому, що обидві сторони межі не згодні. Одна сторона переходить до негативної нескінченності, а інша - до позитивної нескінченності (див. Графік нижче). Якщо ви просто вказуєте DNE, то ви втрачаєте деяку цілком хорошу інформацію про природу функції.
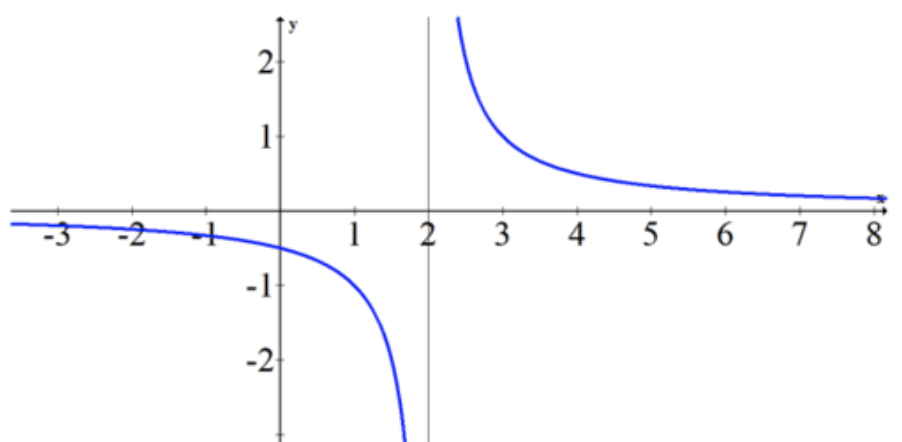
Фонд CK-12 - CCSA
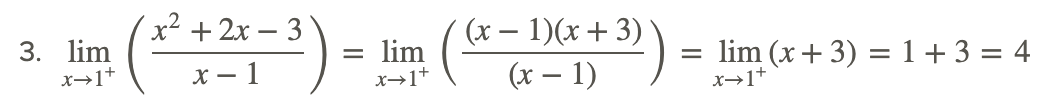
Приклад 4
Оцініть наступні межі.

Приклад 5
Чи є наступна функція безперервна?
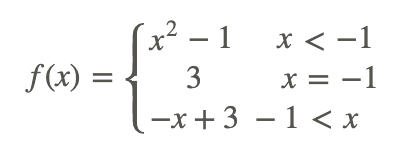
Скористайтеся визначенням безперервності.
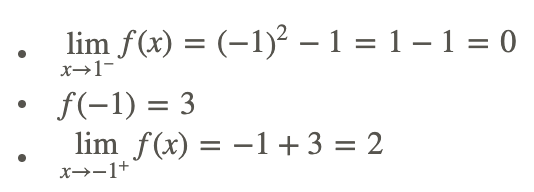
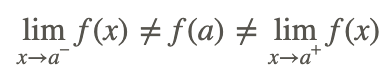
отже ця функція є переривчастою при x = −1. Вона безперервна всюди.
Рецензія
Оцініть наступні межі.
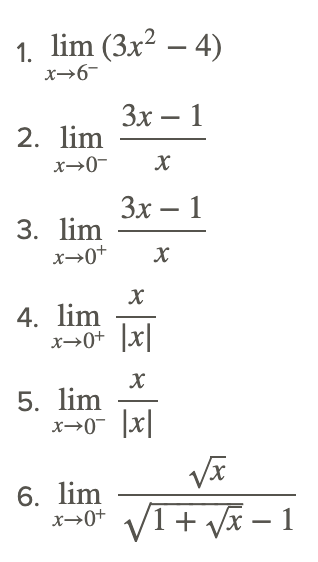
Розглянемо
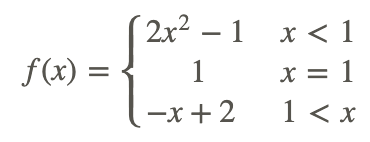
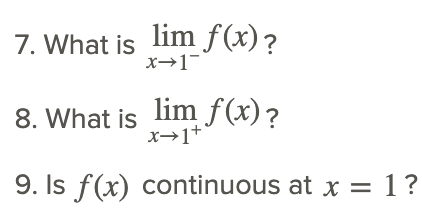
Розглянемо
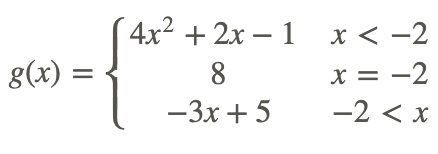
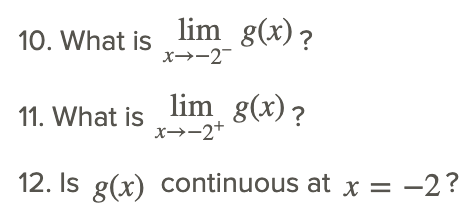
Розглянемо h (x), показані на графіку нижче.
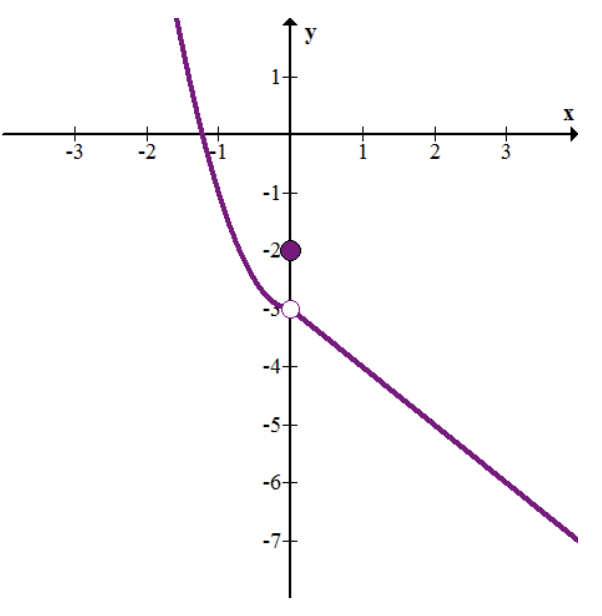
Фонд CK-12 - CCSA
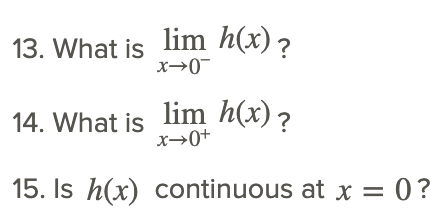
Огляд (Відповіді)
Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 14.6.
Лексика
| Термін | Визначення |
|---|---|
| безперервність | Безперервність для точки існує, коли ліві та праві межі збігаються з функцією, оціненою в цій точці. Щоб функція була неперервною, функція повинна бути неперервною в кожній точці нерозривної області. |
| Безперервний | Безперервність для точки існує, коли ліві та праві межі збігаються з функцією, оціненою в цій точці. Щоб функція була неперервною, функція повинна бути неперервною в кожній точці нерозривної області. |
| стрибок розривів | Зворотні функції - це функції, які «скасовують» один одного. Формально f (x) і g (x) є оберненими функціями, якщо f (g (x)) = g (f (x)) = x. |
| межа | Межа - це значення, до якого наближається вихід функції, коли вхід функції наближається до заданого значення. |
| Знімні розриви | Знімні розриви також відомі як отвори. Вони виникають, коли фактори можуть бути алгебраїчно скасовані від раціональних функцій. |
| Знімний розрив | Знімні розриви також відомі як отвори. Вони виникають, коли фактори можуть бути алгебраїчно скасовані від раціональних функцій. |
| двосторонній межа | Двостороння межа - це значення, до якого наближається функція як з лівого, так і з правого боку. |
Додаткові ресурси
PLIX: Грайте, вчіться, взаємодійте, досліджуйте - односторонні обмеження
Відео: Графічне визначення лімітів та односторонніх меж
Практика: Односторонні типи обмежень
Реальний світ: Глибока заморозка