1.5: Безперервність

Коли ми вивчали межі, ми отримали інтуїцію, яка обмежує міру ``куди прямує функція». Тобто, якщо

$$\lim\limits_{x\to 1} f(x) = 3$$

то, як$x$ близький до 1,$f(x)$ близький до 3. Однак ми бачили, що це не обов'язково хороший показник того, що$f(1)$ насправді є. Це може бути проблематично; функції можуть мати тенденцію до одного значення, але досягати іншого. Цей розділ присвячений функціям, які не проявляють такої поведінки.

Визначення 3 Безперервна функція

$f$Дозволяти функція, визначена на відкритому інтервалі,$I$ що містить$c$.

1. $f$є безперервним при$c$ if$\lim\limits_{x\to c}f(x) = f(c)$.
2. $f$є безперервним,$I$ якщо$f$ є безперервним$c$ для всіх значень$c$ in$I$. Якщо$f$ безперервно$(-\infty,\infty)$ увімкнено, ми говоримо$f$ безперервно скрізь.

Корисним способом встановити, чи$f$ є функція безперервною,$c$ є перевірка наступних трьох речей:

1. $\lim\limits_{x\to c} f(x)$існує,
2. $f(c)$визначено, і
3. $\lim\limits_{x\to c} f(x) = f(c)$.

Приклад 21: Пошук інтервалів безперервності

$f$Дозволяти визначатися, як показано на малюнку 1.25. Дайте інтервал (и), на якому$f$ є безперервним.

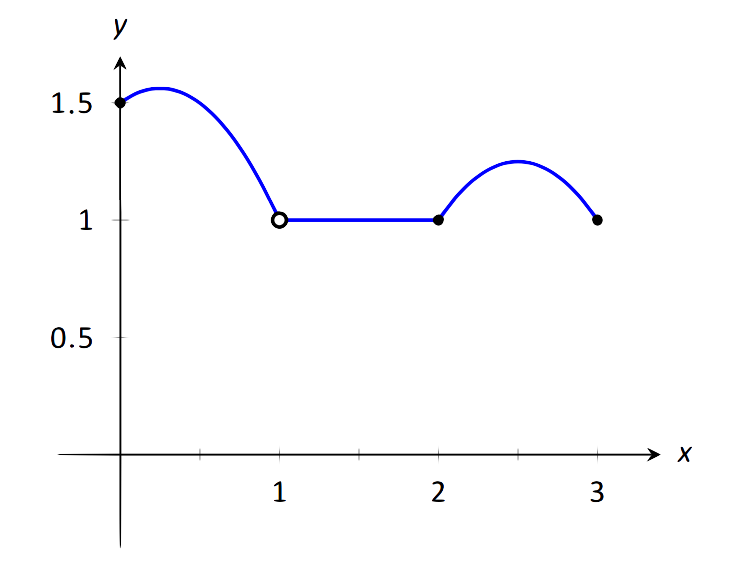
$\text{FIGURE 1.25}$: Графік$f$ у прикладі 21.

Рішення

Приступимо до розгляду трьох критеріїв безперервності.

1. Обмеження$\lim\limits_{x\to c} f(x)$ існують для всіх$c$ між 0 і 3.
2. $f(c)$визначається для всіх$c$ між 0 і 3, за винятком$c=1$. Ми відразу знаємо, що$f$ не може бути безперервним$x=1$.
3. Обмеження$\lim\limits_{x\to c} f(x) = f(c)$ для всіх$c$ між 0 і 3, крім, звичайно, для$c=1$.

Ми робимо висновок, що$f$ є безперервним в кожній точці$(0,3)$ крім в$x=1$. Тому$f$ безперервно включений$(0,1)\cup(1,3)$.

Приклад 22: Пошук інтервалів безперервності

Функція floor повертає найбільше ціле число$f(x) = \lfloor x \rfloor$, менше за вхідні дані$x$. (Наприклад,$f(\pi) = \lfloor \pi \rfloor = 3$.) Графік на$f$ малюнку 1.26 демонструє, чому це часто називають «кроковою функцією».

Дайте інтервали, на яких$f$ безперервно.

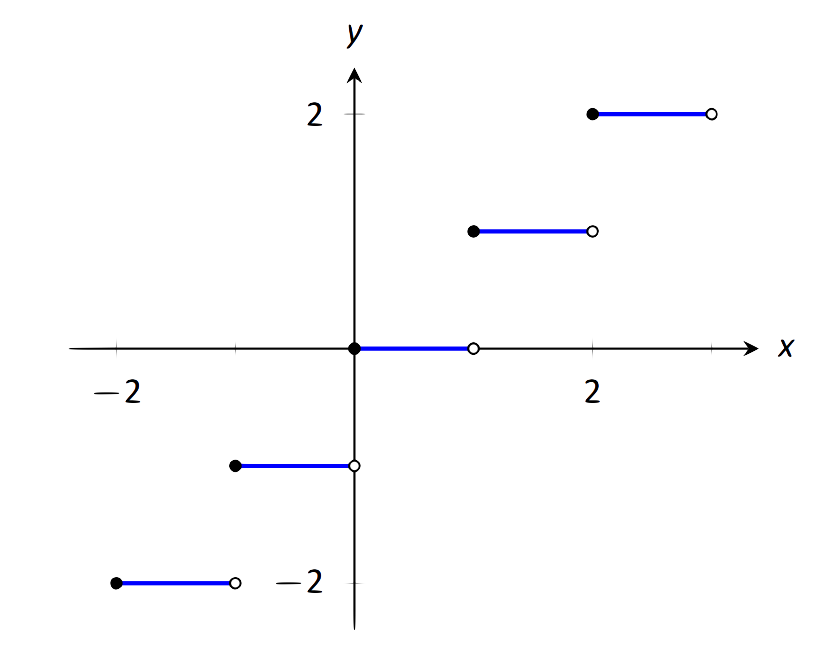
$\text{FIGURE 1.26}$: Графік функції step у прикладі 22.

Рішення

Розглянуто три критерії безперервності.

1. Меж$\lim\limits_{x\to c} f(x)$ не існує при стрибках з одного «кроку» на наступний, які відбуваються при всіх цілих значеннях$c$. Тому обмеження існують для всіх,$c$ крім коли$c$ є цілим числом.
2. Функція визначається для всіх значень$c$.
3. Межа$\lim\limits_{x\to c} f(x) = f(c)$ для всіх значень,$c$ де існує межа, оскільки кожен крок складається лише з рядка.

Зроблено висновок, що$f$ є безперервним скрізь, крім цілих значень$c$. Отже, інтервали, на яких$f$ є безперервним, є $$\ldots, (-2,-1), (-1,0), (0,1), (1,2), \ldots.$$

Наше визначення неперервності на інтервалі визначає інтервал - це відкритий інтервал. Ми можемо розширити визначення безперервності до замкнутих інтервалів, розглядаючи відповідні односторонні межі в кінцевих точках.

Визначення 4: Безперервність на закритих інтервалах

$f$Дозволяти визначатися на замкнутому інтервалі$[a,b]$ для деяких дійсних чисел$a,b$. $f$є безперервним,$[a,b]$ якщо:

1. $f$безперервно ввімкнено$(a,b)$,
2. $\lim\limits_{x\to a^+} f(x) = f(a)$і
3. $\lim\limits_{x\to b^-} f(x) = f(b)$.

Ми можемо внести відповідні корективи, щоб говорити про безперервність на напіввідкритих інтервалах, таких як$[a,b)$ або,$(a,b]$ якщо це необхідно.

Приклад 23: Визначення інтервалів, на яких функція є безперервною

Для кожної з наступних функцій задайте область функції та інтервал (и), на якому вона є безперервною.

1. $f(x) = 1/x$
2. $f(x) = \sin x$
3. $f(x) = \sqrt{x}$
4. $f(x) = \sqrt{1-x^2}$
5. $f(x) = |x|$

Рішення

Оглядаємо кожну по черзі.

1. Домен$f(x) = 1/x$ is$(-\infty,0) \cup (0,\infty)$. Оскільки це раціональна функція, ми застосовуємо теорему 2, щоб визнати, що$f$ є безперервною у всій її області.
2. Домен всіх$f(x) = \sin x$ дійсних чисел, або$(-\infty,\infty)$. Застосування теореми 3 показує, що$\sin x$ є безперервним скрізь.
3. Домен$f(x) = \sqrt{x}$ is$[0,\infty)$. Застосування теореми 3 показує, що$f(x) = \sqrt{x}$ є безперервним у своїй області$[0,\infty)$.
4. Домен$f(x) = \sqrt{1-x^2}$ is$[-1,1]$. Застосування теорем 1 і 3 показує, що$f$ є безперервним на всій його області,$[-1,1]$.
5. Домен$f(x) = |x|$ is$(-\infty,\infty)$. Ми можемо визначити функцію абсолютного значення як$f(x) = \left\{\begin{array}{cc} -x & x<0 \\ x & x\geq 0\end{array}\right.$. Кожен «шматок» цієї кусково визначеної функції є безперервним на всій його області, даючи, що$f$ є безперервним на$(-\infty,0)$ і$[0,\infty)$. Ми не можемо припустити, що$f$ це означає, що це безперервно$(-\infty,\infty)$; нам потрібно перевірити$x=0$ це$\lim\limits_{x\to 0}f(x) = f(0)$, як і точка, де$f$ переходить від одного «шматочка» його визначення до іншого. Легко переконатися, що це дійсно так, отже, ми робимо висновок, що$f(x) = |x|$ безперервно скрізь.

Безперервність за своєю суттю пов'язана з властивостями меж. Через це властивості меж, знайдені в теоремах 1 і 2, також застосовуються до безперервності. Крім того, тепер знаючи визначення неперервності, ми можемо повторно прочитати Теорему 3 як надання списку функцій, які є безперервними у своїх областях. Наступна теорема стверджує, як безперервні функції можуть бути об'єднані для формування інших неперервних функцій, а потім теорема, яка формально перераховує функції, які, як ми знаємо, є неперервними у своїх областях.

Теорема 8: Властивості неперервних функцій

$g$Дозволяти$f$ і бути неперервними функціями на інтервалі$I$, нехай$c$ бути дійсним числом і нехай$n$ бути натуральним числом. Наступні функції є безперервними$I$.

1. Суми/Відмінності:$f\pm g$
2. Постійні кратні:$c\cdot f$
3. Продукція:$f\cdot g$
4. Коефіцієнти:$f/g$ (до тих пір, як$g\neq 0$ на$I$)
5. Повноваження:$f\,^n$
6. Roots:$\sqrt[n]{f}$ (якщо$n$ парне, то$f\geq 0$ on$I$; якщо$n$ непарне, то true для всіх значень$f$ on$I$.)
7. Композиції: Налаштуйте визначення$f$ та$g$ до:$f$ Дозволяти бути безперервним$I$, де діапазон$f$$I$ увімкнено$J$, і нехай$g$ буде безперервним$J$. Потім$g\circ f$$g(f(x))$, тобто безперервно включений$I$.

Теорема 9: Неперервні функції

Наступні функції є безперервними на своїх доменах.

$\begin{align} &1.\, f(x) = \sin x \qquad \qquad \qquad &&2.\, f(x) = \cos x \\ &3.\,f(x) = \tan x &&4.\,f(x) = \cot x \\ &5.\,f(x) = \sec x &&6.\,f(x) = \csc x \\ &7.\,f(x) = \ln x &&8.\,f(x) = \sqrt[n]{x}, \\ &9.\,f(x) = a^x (a>0) &&\,\,\, \text{(where n is a positive integer)} \\ \end{align}$

Ми застосовуємо ці теореми в наступному прикладі.

Приклад 24: Визначення інтервалів, на яких функція є безперервною

Створіть інтервал (и), на якому кожна з наступних функцій є безперервною.

$\begin{align}&1.\,\,f(x) = \sqrt{x-1} + \sqrt{5-x} \qquad \qquad \qquad &&3.\,\,f(x) = \tan x \\ &2.\,\,f(x) = x\sin x &&4.\,\, f(x) = \sqrt{\ln x} \\ \end{align}$

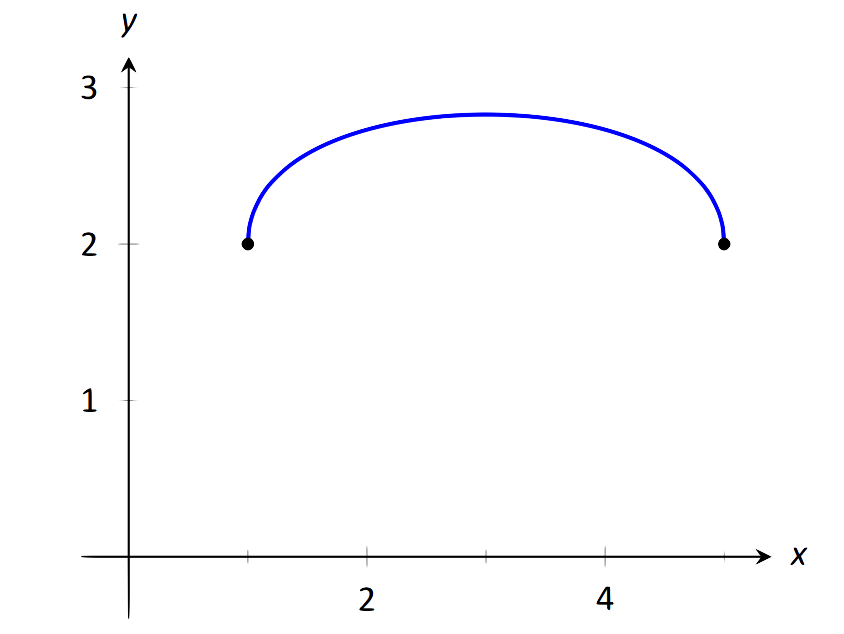
$\text{FIGURE 1.27}$: Графік$f$ у прикладі 24 (а).

Рішення

Розглядаємо кожну по черзі, застосовуючи теореми 8 і 9 відповідно.

1. Терміни квадрат-корінь є неперервними на інтервалах$[1,\infty)$ і$(-\infty,5]$, відповідно. Як$f$ є безперервним тільки там, де кожен член є безперервним,$f$ є безперервним на$[1,5]$, перетин цих двох інтервалів. Графік$f$ наведено на малюнку 1.27.
   
2. Функції$y=x$ і$y=\sin x$ кожен безперервний скрізь, отже, їх продукт теж.
3. Теорема 9 стверджує, що$f(x) = \tan x$ є безперервним «на своїй області». Його домен включає всі дійсні числа, крім непарних кратних$\pi/2$. Таким$f(x) = \tan x$ чином, безперервно на $$\ldots \left(-\frac{3\pi}{2},-\frac{\pi}2\right),\ \left(-\frac{\pi}2,\frac{\pi}2\right),\ \left(\frac{\pi}2,\frac{3\pi}2\right),\ldots,$$ або, еквівалентно, на$D = \{x\in \mathbb{R}\ |\ x\neq n\cdot \frac{\pi}2,\, \text{n is an odd integer} \}.$
4. Домен$y = \sqrt{x}$ is$[0,\infty)$. Діапазон$y=\ln x$ є$(-\infty,\infty)$, але якщо ми обмежуємо його домен до$[1,\infty)$ його діапазону є$[0,\infty)$. Таким чином,$y = \ln x$ обмежуючи домен$[1,\infty)$ обмежує його вихід є$[0,\infty)$, на якому$y = \sqrt{x}$ визначено. Таким чином, домен$f(x) = \sqrt{\ln x}$ є$[1,\infty)$.

Поширений спосіб мислення безперервної функції полягає в тому, що «її графік можна намалювати, не піднімаючи олівець». Тобто його графік утворює «безперервну» криву, без дірок, розривів або стрибків. Незважаючи на те, що виходить за рамки цього тексту, це псевдовизначення блищить деякі тонші точки безперервності. Дуже дивні функції є безперервними, що можна було б важко натиснути, щоб насправді ескіз вручну.

Це інтуїтивне поняття безперервності допомагає нам зрозуміти ще одну важливу концепцію наступним чином. Припустимо$f$, визначається на$[1,2]$ і$f(1) = -10$ і$f(2) = 5$. Якщо$f$ є безперервним$[1,2]$ (тобто його графік може бути замальований як безперервна крива від$(1,-10)$ до$(2,5)$), то ми інтуїтивно знаємо, що десь на$[1,2]$$f$ повинен бути дорівнює$-9$, і$-8$, і$-7,\ -6,\ \ldots,\ 0,\ 1/2,$ т.д. коротше,$f$ бере на себе все проміжні значення між$-10$ і$5$. Це може приймати більше значень;$f$ може насправді дорівнювати 6 в певний час, наприклад, але ми гарантуємо всі значення від$-10$ 5 до 5.

Хоча це поняття здається інтуїтивним, це не тривіально довести, і його важливість є глибокою. Тому поняття викладається у вигляді теореми.

Теорема 10: Теорема про проміжні значення

$f$Дозволяти бути безперервна функція на$[a,b]$ і, без втрати спільності, нехай$f(a) < f(b)$. Тоді для кожного значення$y$, де$f(a) < y < f(b)$, є значення$c$ в$[a,b]$ такому, що$f(c) = y$.

Одним з важливих застосувань теореми проміжних значень є пошук коренів. З огляду на функцію$f$, ми часто зацікавлені в пошуку значень$x$ де$f(x) = 0$. Ці коріння може бути дуже важко знайти точно. Хороші наближення можна знайти за допомогою послідовних застосувань цієї теореми. Припустимо, через прямі обчислення ми знаходимо$f(a) <0 \( and \(f(b)>0$, що, де$a<b$. Теорема про проміжні значення стверджує, що існує$c$ в$[a,b]$ такому, що$f(c) = 0$. Теорема не дає нам жодної підказки про те, де це значення знаходиться в інтервалі$[a,b]$, просто те, що воно існує.

Існує техніка, яка виробляє хороше наближення$c$. $d$Дозволяти бути серединою інтервалу$[a,b]$ і розглянути$f(d)$. Є три можливості:

1. $f(d) = 0$— нам пощастило і натрапили на фактичну вартість. Зупиняємося, як знайшли корінь.
2. $f(d) <0$Тоді ми знаємо, що$f$ на інтервалі є корінь$[d,b]$ - ми вдвічі зменшили розмір нашого інтервалу, отже, ближче до хорошого наближення кореня.
3. $f(d) >0$Тоді ми знаємо, що$f$ на інтервалі є корінь$[a,d]$ - знову ж таки, ми вдвічі зменшили розмір нашого інтервалу, отже, ближче до хорошого наближення кореня.

Послідовне застосування цієї методики називається методом бісекції знаходження коренів. Продовжуємо до тих пір, поки інтервал не стане досить малим. Ми демонструємо це в наступному прикладі.

Приклад 25: Використання методу бісекції

Приблизний корінь$f(x) = x-\cos x$, з точністю до трьох знаків після десяткової.

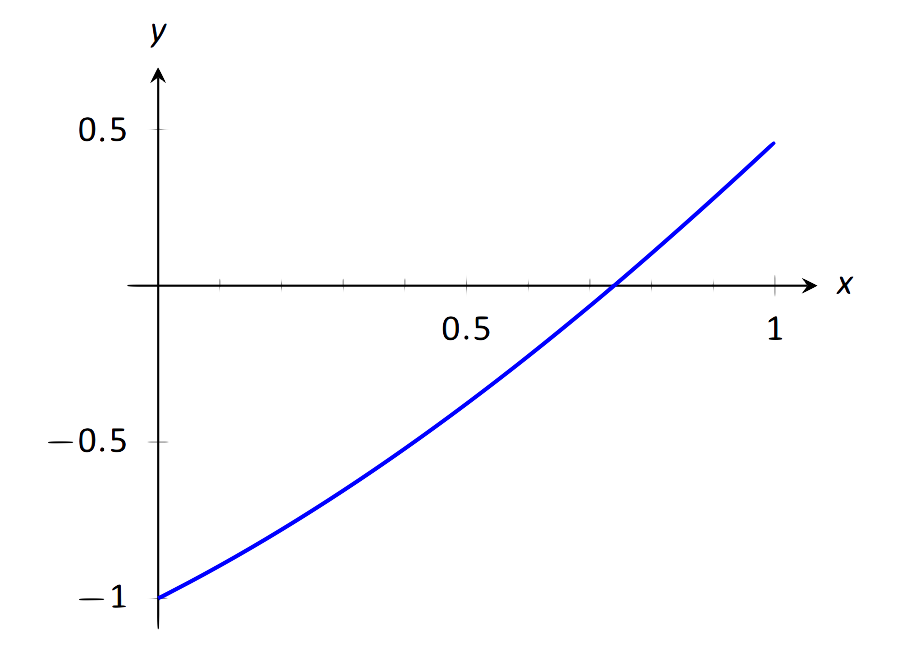
$\text{FIGURE 1.28}$: Графік кореня$f(x) = x-\cos x$.

Рішення

Розглянемо графік$f(x) = x-\cos x$, показаний на малюнку 1.28. Зрозуміло, що графік перетинає$x$ вісь -десь поруч$x=0.8$. Щоб розпочати метод бісекції, виберіть інтервал, який містить$0.8$. Вибираємо$[0.7,0.9]$. Зверніть увагу, що все, що ми дбаємо про це ознаки$f(x)$, а не їх фактичне значення, тому це все, що ми показуємо.

1. Ітерація 1:$f(0.7) < 0$,$f(0.9) > 0$, і$f(0.8) >0$. Тому$0.9$ замініть на$0.8$ і повторіть.
2. Ітерація 2:$f(0.7)<0$$f(0.8) > 0$, і в середній точці$0.75$, у нас є$f(0.75) >0$. Тому$0.8$ замініть на$0.75$ і повторіть. Зверніть увагу, що нам не потрібно продовжувати перевіряти кінцеві точки, лише середню точку. Таким чином ми помістимо решту ітерацій в таблицю 1.29.

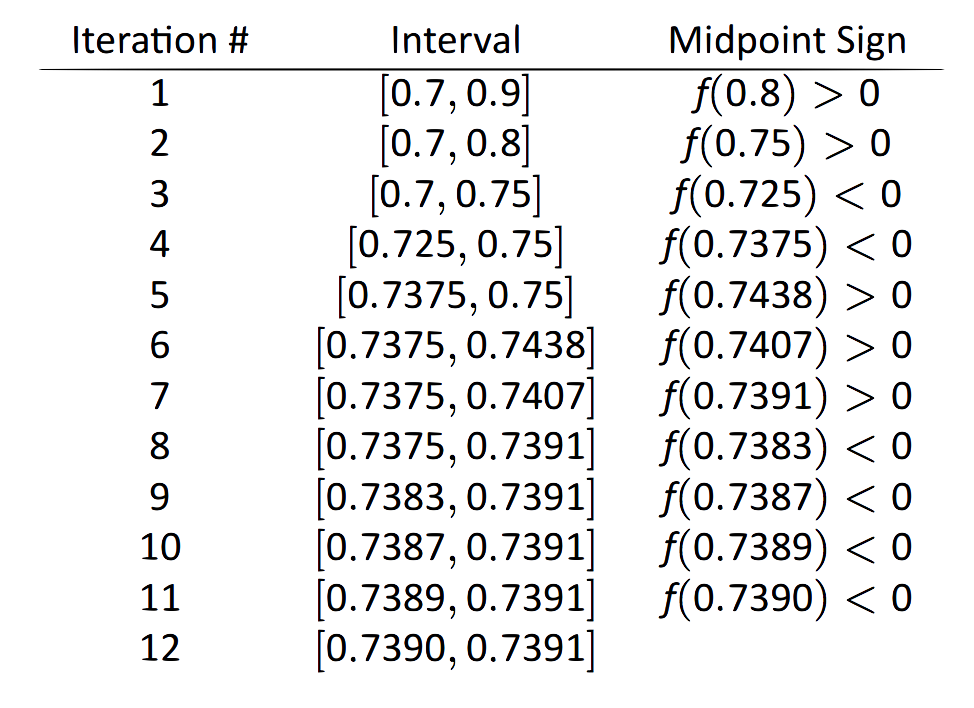
$\text{FIGURE 1.29}$: Ітерації методу бісекцій пошуку коренів

Зверніть увагу, що в 12$^\text{th}$ ітерації ми маємо кінцеві точки інтервалу кожен починаючи з$0.739$. Таким чином, ми звузили нуль до точності перших трьох знаків після десяткової. Використовуючи комп'ютер, у нас є

$$f(0.7390) = -0.00014, \quad f(0.7391) = 0.000024.$$ Будь-яка кінцева точка інтервалу дає хороше наближення де$f$ дорівнює 0. Теорема про проміжні значення стверджує, що фактичний нуль все ще знаходиться в межах цього інтервалу. Хоча ми не знаємо його точного значення, ми знаємо, що це починається з$0.739$.

Цей вид вправ рідко робиться вручну. Швидше, просто запрограмувати комп'ютер для запуску такого алгоритму і зупинки, коли кінцеві точки відрізняються на задану невелику кількість. Один з авторів дійсно написав таку програму і знайшов нуль$f$, з точністю до 10 знаків після десяткового числа, рівним 0.7390851332. Хоча на написання програми знадобилося кілька хвилин, потрібно менше тисячної частки секунди, щоб програма запустила необхідні 35 ітерацій. Менш ніж за 8 сотих секунди нуль обчислювався до 100 знаків після коми (з менш ніж 200 ітераціями).

Проста справа розширити метод бісекції для вирішення проблем, подібних до «Знайти$x$, де»$f(x) = 0$. Наприклад, ми можемо знайти$x$, де$f(x) = 1$. Це насправді працює дуже добре, щоб визначити нову функцію$g$, де$g(x) = f(x) - 1$. Потім використовуйте метод бісекції для вирішення$g(x)=0$.

Аналогічно, задано дві функції$f$ і$g$, ми можемо використовувати метод бісекції для розв'язання$f(x) = g(x)$. Ще раз створіть нову функцію$h$ де$h(x) = f(x)-g(x)$ і вирішуйте$h(x) = 0$.

У розділі 4.1 буде введений інший метод розв'язання рівнянь, який називається Метод Ньютона. У багатьох випадках метод Ньютона набагато швидше. Однак він спирається на більш просунуту математику, тому ми будемо чекати, перш ніж вводити її.

Цей розділ формально визначив, що означає бути безперервною функцією. «Більшість» функцій, з якими ми маємо справу, є безперервними, тому часто здається дивним, щоб формально визначити це поняття. Незалежно від того, це важливо, і становить основу наступної глави.

У наступному розділі ми розглянемо ще один аспект меж: межі, які включають нескінченність.

Автори та авторства

• Template:ContribApexCalc