1.2: Операції над функціями
- Page ID
- 60334
склад функцій
Припустимо, ми хотіли порахувати, скільки коштує обігрів будинку в конкретний день року. Вартість опалення будинку буде залежати від середньодобової температури, а середньодобова температура залежить від конкретного дня року. Зверніть увагу, як ми тільки що визначили два співвідношення: Температура залежить від дня, а вартість залежить від температури. Використовуючи описові змінні, ми можемо відзначити ці дві функції.
Перша функція\(C(T)\), дає витрати\(C\) на опалення будинку, коли середньодобова температура становить\(T\) градуси Цельсія, а друга\(T(d)\), дає середньодобову температуру конкретного міста в день\(d\) року. Якби ми хотіли визначити вартість опалення будинку на п'ятий день року, ми могли б зробити це, зв'язавши наші дві функції воєдино, ідея, яка називається складом функцій. Використовуючи функцію\(T(d)\), ми могли б оцінити,\(T(5)\) щоб визначити середньодобову температуру на п'ятий день року. Потім ми могли б використовувати цю температуру як вхід до\(C(T)\) функції, щоб знайти вартість опалення будинку на п'ятий день року:\(C(T(5))\).
Коли вихід однієї функції використовується як вхід іншої, ми називаємо всю операцію складом функцій. Ми пишемо\(f(g(x))\), і читаємо це як «\(f\)\(g\)з\(x\)» або «\(f\)складений з\(g\) at\(x\)».
Альтернативне позначення для композиції використовує оператор композиції:\(\circ\). \((f\circ g)(x)\)читається «\(f\)з\(g\)\(x\)» або «\(f\)складається з\(g\) at\(x\)», так само, як\(f(g(x))\).
Припустимо,\(c(s)\) дає кількість спалених калорій, роблячи\(s\) присідання, і\(s(t)\) дає кількість присідань, які людина може зробити за\(t\) лічені хвилини. Інтерпретувати\(c(s(3))\).
Рішення
Коли нас просять тлумачити, нас просять пояснити значення виразу словами. Внутрішній вираз в композиції є\(s(3)\). Оскільки вхід у\(s\) функцію - це час, 3 представляє 3 хвилини, і\(s(3)\) це кількість присідань, які можна зробити за 3 хвилини. Прийняття цього виводу та використання його як входу до\(c(s)\) функції дасть нам калорії, які можна спалити за кількістю присідань, які можна зробити за 3 хвилини.
Композиція функцій з використанням таблиць і графіків
При роботі з функціями, заданими у вигляді таблиць і графіків, ми можемо шукати значення для функцій за допомогою наданої таблиці або графіка. Ми починаємо оцінку з наданих вхідних даних, і спочатку оцінюємо внутрішню функцію. Потім ми можемо використовувати вихід внутрішньої функції як вхід до зовнішньої функції. Щоб пам'ятати про це, завжди працюйте зсередини назовні.
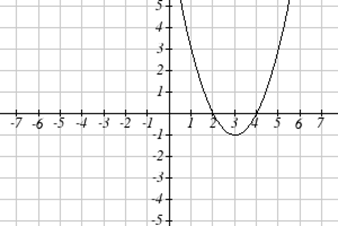
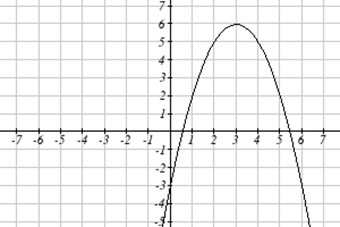
Використовуючи наведені нижче графіки, оцініть\(f(g(1))\).
Рішення
Щоб оцінити\(f(g(1))\), ми знову починаємо з внутрішньої оцінки. Ми оцінюємо\(g(1)\) за допомогою графіка\(g(x)\) функції, знаходячи вхід 1 на горизонтальній осі і знаходячи вихідне значення графіка на цьому вході. Ось,\(g(1)=3\). Використовуючи це значення як вхід до\(f\) функції,\(f(g(1))=f(3)\). Потім ми можемо оцінити це, дивлячись на графік\(f(x)\) функції, знаходячи вхід 3 на горизонтальній осі, і читання вихідного значення графіка на цьому вході. Ось\(f(3)=6\), так\(f(g(1))=6\).
Композиції з використанням формул
При оцінці складу функцій, де ми або створили, або дали формули, концепція роботи зсередини залишається колишньою. Спочатку ми оцінюємо внутрішню функцію, використовуючи надане вхідне значення, потім використовуємо отриманий висновок як вхід до зовнішньої функції.
Дано\(f(t)=t^2-t\) і\(h(x)=3x+2\), оцініть\(f(h(1))\).
Рішення
Оскільки внутрішня оцінка\(h(1)\) ми починаємо з оцінки\(h(x)\) функції на 1:\[h(1)=3(1)+2=5\nonumber \]
Потім\(f(h(1))=f(5)\), таким чином, ми оцінюємо\(f(t)\) функцію на вході 5:\[f(h(1))=f(5)=5^2-5=20\nonumber \]
Однак ми не обмежуємося використанням числового значення в якості входу в функцію. Ми можемо помістити в функцію що завгодно: значення, іншу змінну або навіть алгебраїчний вираз, за умови, що ми використовуємо вхідний вираз скрізь, де ми бачимо вхідну змінну.
Нехай\(f(x)=x^2\) і\(g(x)=\dfrac{1}{x}-2x\). Знайти\(f(g(x))\) і\(g(f(x))\).
Рішення
Щоб знайти\(f(g(x))\), починаємо з оцінки всередині, виписуючи формулу для\(g(x)\):\[g(x)=\dfrac{1}{x}-2x\nonumber \]
Потім ми використовуємо вираз\(\left(\dfrac{1}{x}-2x\right)\) як вхід для функції\(f\):\[f(g(x))=f\left(\dfrac{1}{x}-2x\right)\nonumber \]
Потім ми оцінюємо функцію,\(f(x)\) використовуючи формулу для\(g(x)\) як вхідних даних. З тих\(f(x)=x^2\) пір\[f\left(\dfrac{1}{x}-2x\right)=\left(\dfrac{1}{x}-2x\right)^2\nonumber \]
Це дає нам формулу складу:\[f(g(x))=\left(\dfrac{1}{x}-2x\right)^2\nonumber \]
Аналогічно, щоб знайти\(g(f(x))\), оцінюємо внутрішню частину, виписуючи формулу для\(f(x)\):\(g(f(x))=g(x^2)\).
Тепер оцінюємо функцію,\(g(x)\) використовуючи в\(x^2\) якості входу:\[g(f(x))=\dfrac{1}{x^2}-2x^2\nonumber \]
Сіті-менеджер визначає\(R\), що податкові надходження у мільйони доларів, зібрані на населення у\(p\) тисячах людей\(R(p)=0.03p+\sqrt{p}\), даються за формулою, і що населення міста в тисячах прогнозується слідувати формулі\(p(t)=60+2t+0.3t^2\), де\(t\) вимірюється роками після 2010 року. Знайдіть формулу податкових надходжень як функцію року.
Рішення
Оскільки ми хочемо, щоб податкові надходження були функцією року, ми хочемо, щоб рік був нашим початковим вкладом, а дохід - нашим кінцевим результатом. Щоб знайти дохід, нам доведеться спочатку спрогнозувати населення міста, а потім використовувати цей результат як вхід до податкової функції. Отже, нам потрібно знайти\(R(p(t)).\) Оцінюючи це,\[\begin{align*} R(p(t)) & = R(60+2t+0.3t^2)\\ & = 0.03(60+2t+0.3t^2)+\sqrt{60+2t+0.3t^2} \end{align*}\nonumber \]
Цей склад дає нам єдину формулу, яка може бути використана для прогнозування податкових надходжень протягом певного року, не потребуючи пошуку посередницької вартості населення.
Наприклад, прогнозувати податкові надходження в 2017 році, коли\(t = 7\) (тому що\(t\) вимірюється роками після 2010 року),\[\begin{align*} R(p(7)) & = 0.03\left(60+2(7)+0.3\left(7^2\right)\right)+\sqrt{60+2(7)+0.3\left(7^2\right)}\\ \approx & 12.079\text{ million dollars} \end{align*}\nonumber \]
Пізніше в цьому курсі бажано буде розкласти функцію — записати її як композицію двох простіших функцій.
Напишіть\(f(x)=3+\sqrt{5-x^2}\) як склад двох функцій.
Рішення
Шукаємо дві функції,\(g\) і\(h\), так\(f(x)=g(h(x))\). Для цього шукаємо функцію всередині функції у формулі for\(f(x)\). Як одна з можливостей, ми могли б помітити, що\(5-x^2\) це внутрішня частина квадратного кореня. Потім ми могли б розкласти функцію як:\[h(x)=5-x^2, \quad g(x)=3+\sqrt{x}\nonumber \]
Ми можемо перевірити нашу відповідь, перекомпонувавши функції:\[g(h(x))=g(5-x^2)=3+\sqrt{5-x^2}\nonumber \]
Відзначимо, що це не єдине рішення проблеми. Ще одним нетривіальним розкладанням було б\[h(x)=x^2, \quad g(x)=3+\sqrt{5-x}.\nonumber \]
Перетворення функцій
Перетворення дозволяють нам будувати нові рівняння з наших основних функцій інструментарію. Найосновнішими перетвореннями є зміщення графіка по вертикалі або горизонталі.
Задано функцію\(f(x)\), якщо ми визначимо нову функцію\(g(x)\) як\(g(x)=f(x)+k\), де\(k\) - константа, то\(g(x)\) це вертикальний зсув функції\(f(x)\), де всі вихідні значення були збільшені на\(k\).
Якщо\(k\) позитивний, то графік зміститься вгору. Якщо\(k\) негативний, то графік зміститься вниз.
Задано функцію\(f(x)\), якщо ми визначимо нову функцію\(g(x)\) як\(g(x)=f(x+k)\), де\(k\) - константа, то\(g(x)\) це горизонтальний зсув функції\(f(x)\), де всі вихідні значення були збільшені на\(k\).
Якщо\(k\) позитивний, то графік зміститься вліво. Якщо\(k\) негативний, то графік зміститься вправо.
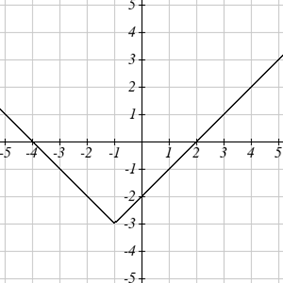
Дано\(f(x)=|x|\), накидаємо графік\(h(x)=f(x+1)-3=|x+1|-3\).
Рішення
Функція\(f\) є нашим інструментарієм функції абсолютного значення. Ми знаємо, що цей графік має форму V, з точкою в початку. Графік\(h\) перетворився двома\(f\) способами:\(f(x+1)\) це зміна на внутрішній стороні функції, що дає горизонтальний зсув вліво на 1, потім віднімання на 3 в\(f(x+1)-3\) - це зміна зовнішньої частини функції, що дає вертикальний зсув вниз на 3. Перетворення графіка дає:
Напишіть формулу для показаного графіка, перетворення інструментарію з функцією квадратного кореня.
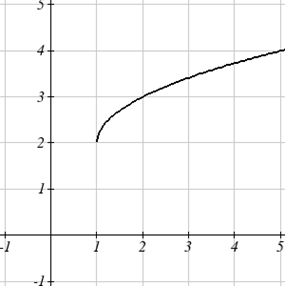
Рішення
Графік функції інструментарію починається з початку, тому цей графік був зміщений на 1 вправо і вгору на 2. У функції позначення, ми могли б написати, що як\(h(x)=f(x-1)+2\). Використовуючи формулу для функції квадратного кореня, ми можемо записати\(h(x)=\sqrt{x-1}+2\).
Зверніть увагу, що це перетворення змінило область і діапазон функції. Цей новий граф має домен\([1,\infty)\) і діапазон\([2,\infty)\).
Іншим перетворенням, яке можна застосувати до функції, є відображення над горизонтальною або вертикальною віссю.
Задано функцію\(f(x)\), якщо ми визначимо нову функцію\(g(x)\) як\(-f(x)\), то\(g(x)\) це вертикальне відображення функції\(f(x)\), іноді зване відображенням навколо осі x
Якщо ми визначимо нову функцію\(g(x)\) як\(f(-x)\), то\(g(x)\) це горизонтальне відображення функції\(f(x)\), іноді називається відображенням про\(y\) -осі.
Загальна модель навчання має рівняння,\(k\) подібне до\(k(t)=-2^t+1\), де відсоток майстерності, який може бути досягнутий після\(t\) практичних занять. Це перетворення функції,\(f(t)=2^t\) показаної тут. Намалюйте графік\(k(t)\).
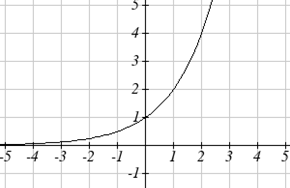
Рішення
Це рівняння об'єднує три перетворення в одне рівняння.
| Горизонтальне відображення: | \(f(-t)=2^{-t}\) | поєднується з |
| вертикальне відображення: | \(-f(-t)=-2^{-t}\) | поєднується з |
| вертикальний зсув вгору на 1: | \(-f(-t)+1=-2^{-t}+1\). |
Ми можемо намалювати графік, застосовуючи ці перетворення по черзі до вихідної функції:
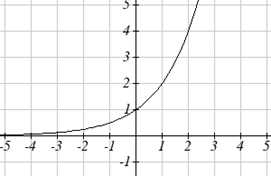
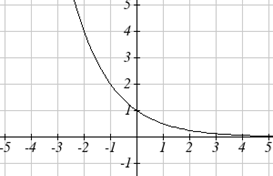
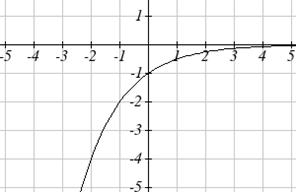
Потім, зрушивши вгору 1, отримуємо остаточний графік:\[k(t)=-f(-t)+1=-2^{-t}+1\nonumber \]
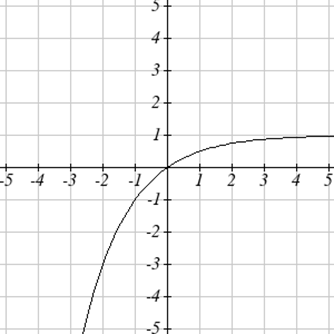
Примітка: Як модель для навчання, ця функція буде обмежена областю\(t\geq 0\), з відповідним діапазоном\([0,1)\).
За допомогою зрушень ми побачили ефект додавання або віднімання до входів або виходів функції. Тепер ми досліджуємо ефекти множення виходів.
Задано функцію\(f(x)\), якщо ми визначимо нову функцію\(g(x)\) як\(g(x)=k\cdot f(x)\), де\(k\) є константою, то\(g(x)\) є вертикальним розтягуванням або стисненням функції\(f(x)\).
- Якщо\(k \gt 1\), то графік буде розтягнутий
- Якщо\(0\lt k \lt 1\), то графік буде стиснутий
- Якщо\(k \lt 0\), то буде поєднання вертикальної розтяжки або стиснення з вертикальним відображенням.
На графіку нижче наведено перетворення функції інструментарію\(f(x)=x^3\). Пов'язати цю нову функцію\(g(x)\)\(f(x)\), а потім знайти формулу для\(g(x)\).
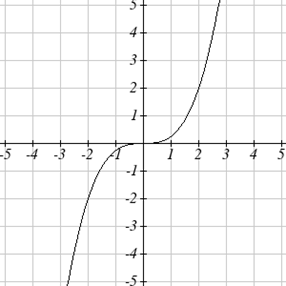
Рішення
При спробі визначити вертикальний розтяг або зсув корисно шукати точку на графіку, яка є відносно чіткою. На цьому графіку, здається, що\(g(2)=2\). З основною кубічною функцією на одному вході,\(f(2)=2^3=8\). Виходячи з цього, виявляється, що\(g\) виходи - це\(\frac{1}{4}\) виходи функції\(f\), оскільки\(g(2)=\frac{1}{4}f(x)\). З цього можна досить сміливо зробити висновок, що\[g(x)=\frac{1}{4}f(x).\nonumber \]
Ми можемо написати формулу для\(g\), скориставшись визначенням функції\(f\):\[g(x)=\frac{1}{4}f(x)=\frac{1}{4}x^3.\nonumber \]
Поєднання перетворень
При комбінуванні вертикальних перетворень дуже важливо враховувати порядок перетворень. Наприклад, вертикальне зміщення на 3, а потім вертикальне розтягування на 2 не створює такий же графік, як розтягування по вертикалі на 2, а потім вертикальне зміщення на 3. Порядок випливає красиво з порядку операцій.
При комбінуванні вертикальних перетворень, написаних у формі\(a\cdot f(x)+k\), спочатку вертикально розтягують на\(a\), потім по вертикалі зрушують на\(k\).
Напишіть рівняння для перетвореного графіка показаної квадратичної функції.
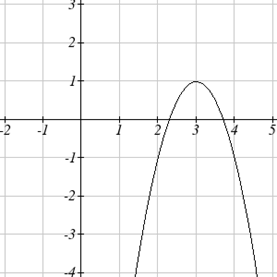
Рішення
Оскільки це квадратична функція, спочатку розглянемо, як виглядає основна квадратична функція набору інструментів і як це змінилося. Спостерігаючи за графіком, ми помічаємо кілька перетворень: оригінальна функція набору інструментів була перевернута над\(x\) віссю, сталося якесь розтягування або стиснення, і ми можемо побачити зсув вправо 3 одиниці і зсув вгору на 1 одиницю. Всього існує чотири операції:
- Вертикальне відображення, що вимагає негативного знака поза функцією.
- Вертикальна розтяжка
- Горизонтальний зсув вправо 3 одиниці, що говорить нам поставити x-3 на внутрішню частину функції.
- Вертикальний зсув вгору 1 одиниця, що говорить нам додати 1 на зовнішній стороні функції.
За спостереженням основна функція набору інструментів має вершину в (0, 0) і симетричні точки в (1, 1) і (-1, 1). Ці точки знаходяться на 1 одиницю вгору і 1 одиницю над вершиною. Нові точки на перетвореному графіку знаходяться на відстані 1 одиниці горизонталі, але 2 одиниці вертикально. Вони були розтягнуті вертикально на 2.
Далеко не кожен може це побачити, просто подивившись на графік. Якщо ви можете, чудово, але якщо ні, ми можемо вирішити за це. Спочатку ми напишемо рівняння для цього графіка, з невідомим вертикальним розтягуванням:
| \(f(x)=x^2\) | Оригінальна функція |
| \(-f(x)=-x^2\) | Вертикально відбивається |
| \(-a\cdot f(x)=-a x^2\) | Вертикально витягнутий |
| \(-a\cdot f(x-3)=-a(x-3)^2\) | Зсунуто вправо 3 |
| \(-a\cdot f(x-3)+1=-a(x-3)^2+1\) | Зсунуто вгору 1 |
Тепер ми знаємо, що наш графік буде мати рівняння форми\(g(x)=-a(x-3)^2+1\). Щоб знайти вертикальну розтяжку, ми можемо визначити будь-яку точку на графіку (крім найвищої точки), наприклад точку (2, -1), яка нам говорить\(g(2)=-1\). Використовуючи нашу загальну формулу, і підставляючи 2 for\(x\), і -1 для\(g(x)\).
Це говорить нам про те, що для створення графіка нам потрібна вертикальна розтяжка на два.
Таким чином, функція, яка виробляє цей графік\[g(x)=-2(x-3)^2+1.\nonumber \]
На якому інтервалі (ах) відбувається\(g(x)=\dfrac{-2}{(x-1)^2}+3\) збільшення і зменшення функції?
Рішення
Це перетворення інструментарію зворотної квадратної функції,\(f(x)=\dfrac{1}{x^2}\)
| \(-2f(x)=\dfrac{-2}{x^2}\) | Вертикальний фліп і вертикальна розтяжка на 2 |
| \(-2f(x-1)=\dfrac{-2}{(x-1)^2}\) | Зсув вправо на 1 |
| \(-2f(x-1)+3=\dfrac{-2}{(x-1)^2}+3\) | Зсув вгору на 3 |
Основна зворотна квадратна функція збільшується\((-\infty,0)\) і зменшується на\((0,\infty)\). Через вертикальне перевертання\(g(x)\) функція буде зменшуватися зліва і збільшуватися праворуч. Горизонтальний зсув вправо на 1 також змістить ці інтервали на правий. З цього ми можемо визначити\(g(x)\) буде збільшуватися\((1,\infty)\) і зменшуватися далі\((-\infty,1)\). Ми також могли б графікувати перетворення, щоб допомогти нам визначити ці інтервали.