1.1: Функції
- Page ID
- 60344
Що таке функція?
Світ природи сповнений взаємозв'язків між величинами, які змінюються. Коли ми бачимо ці відносини, природно для нас запитати Якщо я знаю одну кількість, чи можу я тоді визначити іншу?
Це встановлює ідею вхідної величини, або незалежної змінної, і відповідної вихідної кількості, або залежної змінної. З цього ми отримуємо поняття функціональної залежності, в якій вихід можна визначити за входом.
Для деяких величин, таких як зріст і вік, між цими величинами, безумовно, існують відносини. Враховуючи конкретну людину та будь-який вік, досить легко визначити їх зріст, але якби ми спробували змінити ці стосунки та визначити зріст із заданого віку, це було б проблематично, оскільки більшість людей підтримують однаковий зріст протягом багатьох років.
Функція є правилом для зв'язку між вхідною або незалежною кількістю і виходом, або залежною, величиною, в якій кожне вхідне значення однозначно визначає одне вихідне значення. Ми говоримо, що вихід є функцією входу.
У прикладі зростання та віку вище, чи є висота функцією віку? Чи є вік функцією висоти?
Рішення
У прикладі зростання та віку вище було б правильно сказати, що висота - це функція віку, оскільки кожен вік однозначно визначає висоту. Наприклад, на мій 18-й день народження у мене був рівно один зріст 69 дюймів.
Однак вік не є функцією висоти, оскільки один вхід висоти може відповідати більш ніж одному вихідному віку. Наприклад, для вхідної висоти 70 дюймів, є більше одного виходу віку, оскільки я був 70 дюймів у віці 20 і 21 років.
Функція позначення
Для спрощення виписування виразів і рівнянь за участю функцій часто використовують спрощене позначення. Ми також використовуємо описові змінні, щоб допомогти нам запам'ятати значення величин у задачі.
Замість того, щоб писати висота є функцією віку,
ми могли б використовувати описову змінну\(h\) для представлення висоти, і ми могли б використовувати описову змінну\(a\) для представлення віку.
| «висота - це функція віку» | якщо ми називаємо функцію, яку\(f\) ми пишемо |
| «\(h\)\(f\)є\(a\)» | або простіше |
| \(h = f(a)\) | ми могли б замість цього назвати функцію\(h\) і написати |
| \(h(a)\) | який читається "\(h\)з\(a\)» |
Пам'ятайте, що ми можемо використовувати будь-яку змінну, щоб назвати функцію; позначення\(h(a)\) показує нам, що\(h\) залежить від\(a\). Значення \(a\)
необхідно поставити в функцію, \(h\)
щоб отримати результат. Будьте обережні — дужки вказують на те, що у функцію вводиться вік (Примітка: не плутайте ці дужки з множенням!).
Позначення output =\(f\) (input) визначає функцію з ім'ям\(f\). Це буде зчитування виводу\(f\) з вхідних даних.
Функція\(N = f(y)\) дає кількість поліцейських\(N\), у місті на рік\(y\). Що нам\(f(2005) = 300\) говорить?
Рішення
Коли ми читаємо\(f(2005) = 300\), ми бачимо вхідну кількість 2005, що є значенням для вхідної кількості функції, рік (\(y\)). Вихідне значення 300, кількість поліцейських (\(N\)), значення для вихідної кількості. Запам'ятайте\(N=f(y)\). Це говорить нам про те, що у 2005 році в місті було 300 поліцейських.
Таблиці як функції
Функції можуть бути представлені різними способами: Words (як ми робили в останніх кількох прикладах), таблиці значень, графіки або формули. Представлений у вигляді таблиці, нам представлений список вхідних і вихідних значень.
Ця таблиця відображає вік дітей в роках і відповідні їм висоти. Хоча деякі таблиці показують всю інформацію, яку ми знаємо про функцію, ця конкретна таблиця представляє лише деякі дані, доступні для росту та віку дітей.
| (вхід)\(a\), вік в роках | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|
| (вихід)\(h\), висота в дюймах | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
Яка з цих таблиць визначає функцію (якщо така є)?
| Вхідні | Вихід |
|---|---|
| 2 | 1 |
| 5 | 3 |
| 8 | 6 |
| Вхідні | Вихід |
|---|---|
| -3 | 5 |
| 0 | 1 |
| 4 | 5 |
| Вхідні | Вихід |
|---|---|
| 1 | 0 |
| 5 | 2 |
| 5 | 4 |
Рішення
Перша і друга таблиці визначають функції. В обох кожному вході відповідає рівно один вихід. Третя таблиця не визначає функцію, оскільки вхідне значення 5 відповідає двом різним вихідним значенням.
Розв'язування та оцінка функцій
Коли ми працюємо з функціями, ми робимо дві типові речі: оцінюємо та вирішуємо. Оцінка функції - це те, що ми робимо, коли знаємо вхід, і використовуємо функцію для визначення відповідного виходу. Оцінювання завжди дасть один результат, оскільки кожен вхід функції відповідає рівно одному виводу.
Рішення рівнянь за участю функції - це те, що ми робимо, коли ми знаємо вихід, і використовуємо функцію для визначення входів, які будуть виробляти цей вихід. Рішення функції може призвести до більш ніж одного рішення, оскільки різні входи можуть давати однаковий вихід.
Використовуючи наведену таблицю, де\(Q=g(n)\)
| \(n\) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| \(Q\) | 8 | 6 | 7 | 6 | 8 |
- Оцінити\(g(3)\)
- Вирішити\(g(n)=6\)
Рішення
- Оцінювати\(g(3)\): Оцінка\(g(3)\) (читай:
g з 3
) означає\(Q\), що нам потрібно визначити вихідне значення функції g з урахуванням вхідного значення\(n=3\). Дивлячись на таблицю, ми бачимо вихід, відповідний\(n=3\) is\(Q=7\), що дозволяє зробити висновок\(g(3) = 7\). - Вирішити\(g(n)=6\): Рішення\(g(n) = 6\) означає, що нам потрібно визначити, які вхідні значення\(n\), виробляти вихідне значення 6. Дивлячись на таблицю, ми бачимо, що є два рішення:\(n = 2\) і\(n = 4\). Коли ми вводимо 2 в функцію\(g\), наш вихід є\(Q = 6\). Коли ми вводимо 4 в функцію\(g\), наш вихід також\(Q = 6\).
Графіки як функції
Часто графік зв'язку може бути використаний для визначення функції. За умовністю графіки зазвичай створюються з вхідною величиною вздовж горизонтальної осі та вихідною величиною вздовж вертикалі.
Який з цих графіків визначає функцію\(y=f(x)\)?
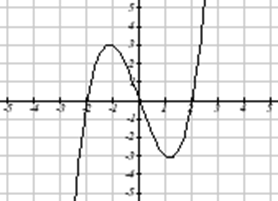
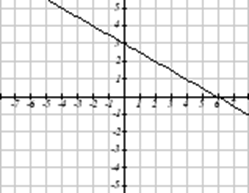
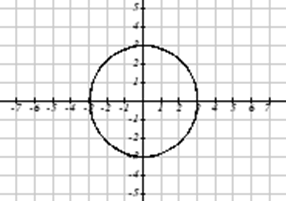
Рішення
Дивлячись на три графіки вище, перші два визначають функцію\(y=f(x)\), так як для кожного вхідного значення вздовж горизонтальної осі є рівно одне відповідне вихідне значення, яке визначається значенням y графіка. Третій графік не визначає функцію,\(y=f(x)\) оскільки деякі вхідні значення, наприклад\(x=2\), відповідають більш ніж одному вихідному значенню.
Тест вертикальної лінії - це зручний спосіб подумати про те, чи визначає графік вертикальний вихід як функцію горизонтального входу. Уявіть, що ви малюєте вертикальні лінії через графік. Якщо будь-яка вертикальна лінія перетинає графік більше одного разу, то графік не визначає лише один вертикальний вихід для кожного горизонтального входу.
Для оцінки функції за допомогою графіка потрібно взяти заданий вхід і використовувати графік для пошуку відповідного результату. Розв'язування рівняння функції за допомогою графіка вимагає взяття заданого виходу і перегляду графіка для визначення відповідного входу.
З огляду на наведену нижче графіку,
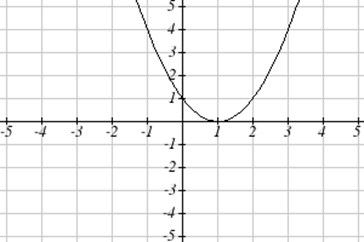
- Оцінити\(f(2)\).
- Вирішити\(f(x) = 4\).
Рішення
- Для оцінки\(f(2)\) знаходимо вхід по\(x=2\) горизонтальній осі. Переміщення вгору до графіка дає точку (2, 1), що дає вихід\(y=1\). Отже\(f(2) = 1\).
- Щоб вирішити\(f(x) = 4\), ми знаходимо значення 4 на вертикальній осі, тому що якщо\(f(x) = 4\) тоді 4 - це вихід. Переміщення по горизонталі по графіку дає дві точки з виходом 4: (-1,4) і (3,4). Вони дають два рішення\(f(x) = 4\):\(x = -1\) або\(x = 3\). Це означає\(f(3)=4\),\(f(-1)=4\) і, або коли вхід -1 або 3, вихід дорівнює 4.
Зверніть увагу, що в той час як графік у попередньому прикладі є функцією, отримання двох вхідних значень для вихідного значення 4 показує нам, що ця функція не один до одного.
Формули як функції
Коли це можливо, дуже зручно визначати відносини за допомогою формул. Якщо є можливість висловити висновок у вигляді формули, що включає вхідну величину, то ми можемо визначити функцію.
Висловіть відносини\(2n + 6p = 12\) як функцію,\(p = f(n)\) якщо це можливо.
Рішення
Щоб висловити відносини в цій формі, нам потрібно вміти писати відносини, де\(p\) є функція\(n\), що означає писати його як\(p =\) [щось пов'язане\(n\)].
| \(2n + 6p = 12\) | відняти\(2n\) з обох сторін |
| \(6p = 12 - 2n\) | розділити обидві сторони на 6 і спростити |
\[p=\frac{12-2n}{6}=\frac{12}{6}-\frac{2n}{6}=2-\frac{1}{3}n\nonumber \]
Переписавши формулу як\(p=\), тепер ми можемо висловити\(p\) як функцію:\(p=f(n)=2-\frac{1}{3}n\)
Далеко не кожен зв'язок може бути виражений у вигляді функції за допомогою формули.
Як і у випадку з таблицями та графіками, прийнято оцінювати та вирішувати функції, що включають формули. Оцінка зажадає заміни вхідної змінної в формулі на надане значення і обчислення. Рішення вимагатиме заміни вихідної змінної у формулі на надане значення та рішення для вхідних даних, які б дали цей вихід.
З огляду на функцію\(k(t)=t^3+2\):
- Оцінити\(k(2)\).
- Вирішити\(k(t)=1\).
Рішення
- Для оцінки\(k(2)\) ми вставляємо вхідне значення 2 у формулу всюди, де ми бачимо вхідну змінну\(t\), а потім спрощуємо:\[\begin{align*}k(2) & = 2^3+2\\k(2) & = 8+2 \end{align*}\nonumber \] Отже\(k(2) = 10\).
- Для вирішення задаємо формулу\(k(t) = 1\),\(k(t)\) рівну 1, і вирішуємо для вхідного значення, яке дасть цей вихід:\[\begin{align*} k(t) & = 1 & \\ t^3+2 & = 1 &\text{substitute the original formula} \\ t^3 & = -1 &\text{subtract 2 from each side} \\ t & = 1 &\text{take the cube root of each side} \end{align*}\nonumber \]
Вирішуючи рівняння за допомогою формул, ви можете перевірити свою відповідь, використовуючи своє рішення у вихідному рівнянні, щоб перевірити, чи правильно розрахована відповідь.
Ми хочемо знати, чи\(k(t) = 1\) правда коли\(t=-1\):\[\begin{align*}k(-1) & = (-1)^3+2\\ & = -1+2\\ & = 1,\end{align*}\nonumber \] який був бажаний результат.
Основні функції інструментарію
Є деякі основні функції, які корисно знати назву та форму. Ми називаємо їх основним інструментарієм функцій.
Для цих визначень ми будемо використовувати\(x\) як вхідну змінну і\(f(x)\) як вихідну змінну.
| Лінійний | |
| Постійна: | \(f(x)=c\), Де\(c\) константа (число) |
| Ідентичність: | \(f(x)=x\) |
| Абсолютне значення: | \(f(x)=|x|\) |
| Потужність | |
| Квадратичний: | \(f(x)=x^2\) |
| Кубічний: | \(f(x)=x^3\) |
| Взаємний: | \(f(x)=\frac{1}{x}\) |
| Відповідний квадрат: | \(f(x)=\frac{1}{x^2}\) |
| Квадратний корінь: | \(f(x)=\sqrt[2]{x}=\sqrt{x}\) |
| Кубичний корінь: | \(f(x)=\sqrt[3]{x}\) |
Графіки функцій інструментарію
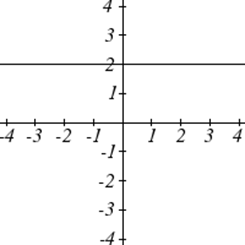
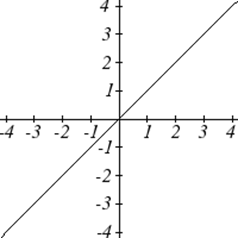
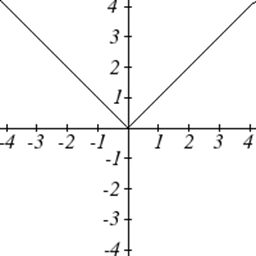
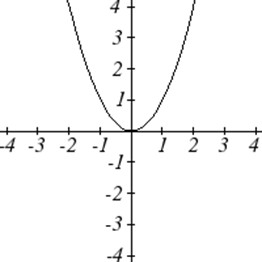
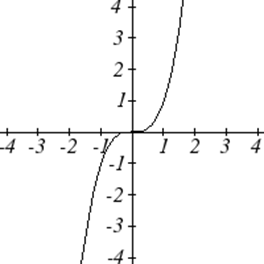
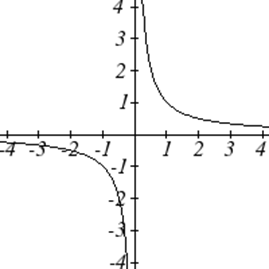
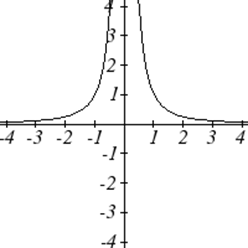
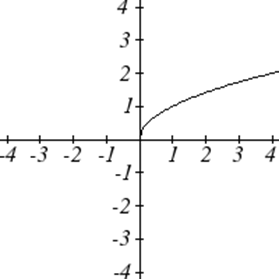
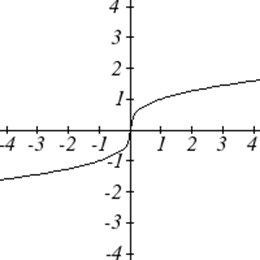
Однією з наших головних цілей в математиці є моделювання реального світу за допомогою математичних функцій. При цьому важливо пам'ятати про обмеження тих моделей, які ми створюємо.
Ця таблиця показує залежність між окружністю і висотою дерева в міру його зростання.
| Окружність,\(c\) | 1.7 | 2.5 | 5.5 | 8.2 | 13,7 |
| Висота,\(h\) | 24.5 | 31 | 45.2 | 54.6 | 92.1 |
Хоча між ними існує сильний зв'язок, безумовно, було б смішно говорити про дерево з окружністю -3 футів або висотою 3000 футів. Коли ми виявляємо обмеження на входи та виходи функції, ми визначаємо область та діапазон функції.
- Домен: набір можливих вхідних значень функції.
- Діапазон: множина можливих вихідних значень функції
Використовуючи таблицю дерева вище, визначте розумний домен і діапазон.
Рішення
Ми могли б об'єднати надані дані з власним досвідом та розумом, щоб наблизити область та діапазон функції\( h = f(c)\). Для домену можливі значення для вхідної окружності c, немає сенсу мати негативні значення, так що\(c > 0\). Ми могли б зробити освічене припущення при максимально розумному значенні, або подивитися, що максимальна вимірювана окружність становить близько 119 футів. З цією інформацією ми б сказали, що розумним доменом є ноги.
Аналогічно для діапазону, не має сенсу мати негативні висоти, і максимальна висота дерева може бути розглянута до 379 футів, тому розумний діапазон - це ноги.
Більш компактною альтернативою позначенню нерівності є інтервальні позначення, в яких інтервали значень позначаються початковим і кінцевим значеннями. Вигнуті дужки використовуються для строго менше,
а квадратні дужки використовуються для менше або рівні.
Оскільки нескінченність не є числом, ми не можемо включити її в інтервал, тому ми завжди використовуємо вигнуті дужки з\(\infty\) і\(-\infty\). Таблиця нижче допоможе вам побачити, як нерівності відповідають інтервальним позначенням:
| Нерівність | Інтервальні позначення |
|---|---|
| \( 5 \lt h \leq10 \) | (5, 10] |
| \(5\leq h \lt10 \) | [5, 10) |
| \(5 \lt h \lt 10\) | (5, 10) |
| \(h \lt10\) | \((-\infty,10)\) |
| \(h\geq10\) | \([10,\infty)\) |
| Усі дійсні числа (\(\mathbb{R}\)) | \((-\infty,\infty)\) |
Опишіть інтервали значень, показані на лінійному графіку нижче, використовуючи конструктор множини та інтервальні позначення:

Рішення
Для опису значень\(x\), які лежать в інтервалах, показаних вище, ми б сказали, \(x\)є дійсним числом більше або дорівнює 1 і менше або дорівнює 3, або дійсне число більше 5.
Як нерівність це \(1\leq x\leq 3\)або\(x \gt 5 \)
. У інтервальних позначеннях він є \([1,3]\cup(5,\infty)\)
.
Знайдіть домен кожної функції:
- \(f(x)=2\sqrt{x+4}\)
- \(g(x)=\dfrac{3}{6-3x}\)
Рішення
- Оскільки ми не можемо взяти квадратний корінь від'ємного числа, нам потрібно, щоб внутрішня частина квадратного кореня була невід'ємною. \(x+4\geq 0\)коли\(x\geq -4\), так домен\(f(x)\) є\([-4,\infty)\).
- Ми не можемо розділити на нуль, тому нам потрібно, щоб знаменник був ненульовим. \(6-3x=0\)коли\(x = 2\), тому ми повинні виключити 2 з домену. Домен\(g(x)\) is\((-\infty,2)\cup(2,\infty)\).
