1.5: Квадратика
- Page ID
- 60316
Квадратики - це перетворення функції\( f(x)=x^2 \). Квадратика зазвичай виникає через проблеми, пов'язані з рухом площі та снаряда, забезпечуючи деякі цікаві програми.
Фермер на задньому дворі хоче обкласти прямокутний простір для нового саду. Вона придбала 80 футів дротяної огорожі, щоб обкласти три сторони, і поставить четверту сторону проти паркану заднього двору. Знайдіть формулу для площі, огородженої парканом, якщо сторони огорожі перпендикулярні існуючому паркану мають довжину\(L\).
Рішення
У такому сценарії, що включає геометрію, часто корисно намалювати малюнок. Також може бути корисно ввести тимчасову змінну\(W\), щоб представляти сторону огорожі паралельно четвертій стороні або задньому дворі паркан.
Оскільки ми знаємо, що у нас є лише 80 футів паркану, ми знаємо\( L+W+L=80 \), що, або простіше кажучи,\( 2L+W=80 \). Це дозволяє нам представляти ширину\(W\), з точки зору\(L\):\( W=80-2L \)
Тепер ми готові написати рівняння для площі, яку огороджує паркан. Ми знаємо, що площа прямокутника - це довжина, помножена на ширину\( A=LW=L(80-2l) \), отже,\[ A(L)=80L-2L^2. \nonumber \] ця формула представляє площу огорожі в перерахунку на змінну довжину\(L\).
Місцева газета в даний час має 84 000 передплатників, щоквартально стягуючи $30. Дослідження ринку припускають, що якби вони підняли ціну до 32 доларів, вони втратять 5000 передплатників. Припускаючи, що підписки лінійно пов'язані з ціною, створіть рівняння для моделювання їх доходу як функції квартального збору.
Рішення
Дохід - це сума грошей, яку компанія приносить. В цьому випадку дохід можна дізнатися, помноживши плату за підписку на кількість передплатників на кількість передплатників. Ми можемо ввести змінні,\(C\) за плату за підписку та\(S\) кількість абонентів, даючи нам рівняння:
Дохід =\(C S\)
Так як кількість передплатників змінюється разом з ціною, нам потрібно знайти зв'язок між змінними.
Ми знаємо, що в даний час\(S = 84,000\) і\(C = 30\), і що якщо вони підвищать ціну до 32 доларів, вони втратять 5000 підписників, даючи другу пару значень,\(S = 79,000\) і\(C = 32\). З цього ми можемо знайти лінійне рівняння, що стосується двох величин. Розглядаючи\(C\) як вхід і\(S\) як вихід, рівняння матиме форму\(S = mC + b\). Ухил буде
\[m = \dfrac{79,000 - 84,000}{32-30} = \dfrac{-5,000}{2} = -2,500\nonumber \]Це говорить нам, що папір втратить 2500 передплатників за кожен долар, який вони підвищують ціну. Потім ми можемо вирішити для вертикального перехоплення.
\[S = -2500C + b\nonumber \]
Підключіть точку\(S = 84,000\) і\(C = 30\)
\[84000 = -2500(30) + b\nonumber \]
Вирішити для\(b\)
\[b = 159,000\nonumber \]
Це дає нам лінійне рівняння,\(S = -2,500C + 159,000\) що стосується вартості та абонентів. Зверніть увагу, що це рівняння попиту, де\(C\) ціна та\(S\) кількість, яку потрібно. Тепер ми повернемося до нашого рівняння доходів.
Дохід =\(C S\)
Підставляємо рівняння для\(S\) зверху:
Виручка =\(C \left(-2,500C + 159,000\right)\)
Розширення
доходу =\(-2,500C^2 + 159,000C\)
Тепер у нас є квадратне рівняння доходу як функція плати за підписку. Пізніше в курсі ми будемо використовувати такі рівняння, щоб визначити ціну, яку потрібно стягувати, щоб максимізувати дохід.
Стандартною формою квадратичної функції є\( f(x)=ax^2+bx+c \).
Форма перетворення квадратичної функції є\( f(x)=a(x-h)^2+k \).
Вершина квадратичної функції розташована за адресою\((h, k)\), де\(h\) і\(k\) знаходяться числа у формі перетворення функції. Оскільки вершина з'являється у формі перетворення, її часто називають формою вершини.
Напишіть рівняння для квадратичного графіка нижче як перетворення\( f(x)=x^2 \).
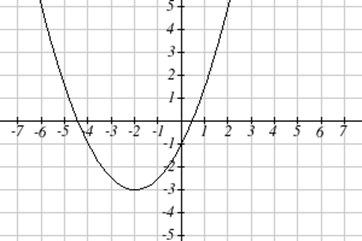
Рішення
Ми бачимо, що графік є основним квадратичним зміщенням вліво 2 і вниз 3, ставлячи вершину на\((-2, -3)\), даючи формулу у вигляді\( g(x)=a(x+2)^2-3 \). Підключивши точку, яка падає на сітку, наприклад\((0,-1)\), ми можемо вирішити для коефіцієнта розтягування:\[\begin{align*} -1 & = a(0+2)^2-3 \\ 2 & = 4a \\ a & = \frac{1}{2} \end{align*}\nonumber \]
Рівняння для цієї формули є\[ g(x)=\frac{1}{2}(x+2)^2-3 \nonumber \]
Короткострокова поведінка: Перехоплення
Як і будь-яка функція, ми можемо знайти вертикальні перехоплення квадратичного, оцінюючи функцію на вході нуля, і ми можемо знайти горизонтальні перехоплення, вирішуючи, коли вихід буде нульовим. Зверніть увагу, що залежно від розташування графіка, ми могли б мати нуль, один або два горизонтальних перехоплення.
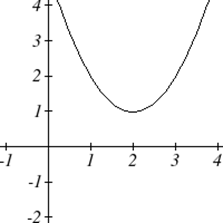
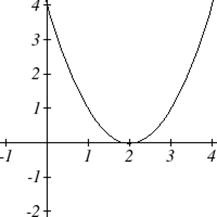
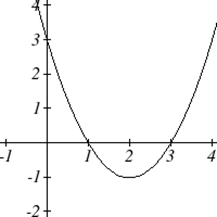
Зверніть увагу, що в стандартній формі квадратики постійний член\(c\) виявляє вертикальний перехоплення графа, так як\( f(0)=a(0)^2+b(0)+c=c \).
Знайдіть вертикальні і горизонтальні перехоплення квадратики\( f(x)=3x^2+5x-2 \).
Рішення
Ми можемо знайти вертикальний перехоплення, оцінюючи функцію на вході нуля:\[f(0)=3(0)^2+5(0)-2=-2\nonumber \] Таким чином, вертикальний перехоплення знаходиться в (0, -2)
Для горизонтальних перехоплень ми вирішуємо, коли вихід буде нульовим:\[0=3x^2+5x-2.\nonumber \] У цьому випадку квадратик може бути легко врахований, забезпечуючи найпростіший метод для вирішення.:\[0=(3x-1)(x+2),\nonumber \] так\[ \begin{align*} 0 & = 3x-1\\ x & = \frac{1}{3} \end{align*} \nonumber \] або\[ \begin{align*} 0 & = x+2\\ x & = -2 \end{align*} \nonumber \] так горизонтальні перехоплення знаходяться в\( \left(\frac{1}{3},0\right) \) і\((-2,0)\).
Коли квадратик не є факторним або його важко фактор, ми можемо звернутися до квадратичної формули.
Для квадратичної функції, заданої в стандартному вигляді\( f(x)=ax^2+bx+c \), квадратична формула дає горизонтальні перехоплення графіка цієї функції:\[ x=\frac{-b\pm \sqrt{b^2-4ac}}{2a} \nonumber \]
М'яч кидається вгору з вершини 40 футів висотою будівлі зі швидкістю 80 футів в секунду. Висота кулі над землею може бути змодельована рівнянням\[ H(t)=-16t^2+80t+40 .\nonumber \] Коли м'яч потрапляє в землю?
Рішення
Щоб знайти, коли м'яч вдариться об землю, нам потрібно визначити, коли висота дорівнює нулю, т. Е\(H(t) = 0\). Хоча ми могли б зробити це за допомогою форми перетворення квадратичного, ми також можемо використовувати квадратичну формулу:\[ t=\frac{-80\pm \sqrt{80^2-4(-16)(40)}}{2(-16)}=\frac{-80\pm\sqrt{8960}}{-32} \nonumber \]
Оскільки квадратний корінь не спрощує красиво, ми можемо скористатися калькулятором для наближення значень рішень:\[ t=\frac{-80-\sqrt{8960}}{-32}\approx 5.458 \quad\text{or}\quad t=\frac{-80+\sqrt{8960}}{-32}\approx -0.458 \nonumber \]
Друга відповідь знаходиться поза розумною сферою нашої моделі, тому ми робимо висновок, що м'яч вдарить об землю приблизно через 5.458 секунд.
Пропозиція для певного товару може бути змодельована,\(p = 3q^2\) а попит може бути змодельований\(p = 1620 - 2q^2\), де\(p\) ціна в доларах, а\(q\) кількість в тисячах найменувань. Знайдіть рівноважну ціну та кількість.
Рішення
Нагадаємо, що рівноважна ціна і кількість знаходять, знаходячи, де перетинаються криві попиту і пропозиції. Ми можемо знайти це, встановивши рівняння рівні:\[3q^2 = 1620 - 2q^2\nonumber\]
Додайте\(2q^2\) в обидві сторони:\(5q^2 = 1620\)
Розділіть на 5 з обох сторін:\(q^2 = 324\)
Візьміть квадратний корінь з обох сторін:\[q = \pm \sqrt{324} = \pm 18 \nonumber\]
Оскільки говорити про негативні величини немає сенсу, рівноважна кількість є\(q = 18\). Щоб знайти рівноважну ціну, оцінюємо будь-яку функцію за рівноважною величиною. \[p = 3(18)^2 = 972\nonumber\]
Рівновага становить 18 тисяч предметів, за ціною $972.
