1.7: Експоненціальні функції
- Page ID
- 60325
Розглянемо ці дві компанії:
- Компанія А має 100 магазинів і розширюється, відкриваючи 50 нових магазинів на рік
- Компанія B має 100 магазинів, і розширюється за рахунок збільшення кількості магазинів на 50% від їх загальної кількості щороку.
Компанія А демонструє лінійне зростання. У лінійному зростанні ми маємо постійну швидкість зміни — постійне число, яке випуск збільшувався за кожне збільшення вхідних даних. Для компанії А кількість нових магазинів на рік однакова щороку.
Компанія B відрізняється - у нас є відсоток змін, а не постійна кількість магазинів/рік, як наша швидкість зміни. Щоб побачити значимість цієї різниці, порівняйте 50% збільшення, коли є 100 магазинів, до 50% збільшення, коли є 1000 магазинів:
- 100 магазинів, збільшення на 50% становить 50 магазинів у цьому році.
- 1000 магазинів, збільшення на 50% становить 500 магазинів у цьому році.
Розрахувавши кількість магазинів через кілька років, ми можемо наочно побачити різницю в результатах.
| Років | Компанія А | Компанія B |
| 2 | 200 | 225 |
| 4 | 300 | 506 |
| 6 | 400 | 1139 |
| 8 | 500 | 2563 |
| 10 | 600 | 5767 |
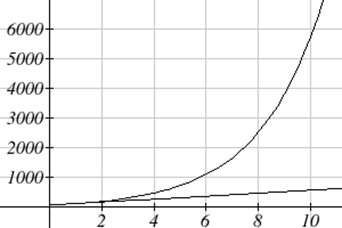
Цей відсоток зростання можна змоделювати за допомогою експоненціальної функції.
Функція експоненціального зростання або розпаду - це функція, яка зростає або скорочується з постійною швидкістю зростання відсотків. Рівняння можна записати у вигляді\[ f(x)=a(1+r)^x\nonumber \] або\[ f(x)=ab^x\nonumber \] де\( b=1+r \).
Де
- \(a\)початкове або початкове значення функції,
- \(r\)- відсоток зростання або швидкості розпаду, записаний у вигляді десяткового числа,
- \(b\)є фактором росту або мультиплікатором зростання. Оскільки сили від'ємних чисел поводяться дивно,\(b\) обмежуємося позитивними значеннями.
Населення Індії становило 1,14 мільярда в 2008 році і зростає приблизно на 1,34% щороку. Напишіть експоненціальну функцію для населення Індії та використовуйте її для прогнозування населення у 2020 році.
Рішення
Використовуючи 2008 як наш час початку (\(t = 0\)), наше початкове населення становитиме 1,14 мільярда. Оскільки відсоток зростання становив 1,34%, наше значення\(r\) становить 0,0134.
Використовуючи базову формулу експоненціального зростання,\(f(x)=a(1+r)^x\) ми можемо написати формулу,\[f(t)=1.14(1+0.0134)^{t}\nonumber \]
Щоб оцінити чисельність населення в 2020 році, ми оцінюємо функцію на\(t = 12\), оскільки 2020 рік становить 12 років після 2008 року:\[f(t)=1.14(1+0.0134)^{12}\approx 1.337 \text{ billion people in 2020.}\nonumber \]
Депозитний сертифікат (CD) - це тип ощадного рахунку, пропонованого банками, як правило, пропонує більш високу процентну ставку в обмін на фіксований проміжок часу, який ви залишите вкладені гроші. Якщо банк пропонує 24-місячний компакт-диск із річною процентною ставкою 1,2%, що збільшується щомісяця, скільки буде інвестиція в розмірі 1000 доларів за ці 24 місяці?
Рішення
По-перше, ми повинні помітити, що процентна ставка є річною ставкою, але складається щомісяця, тобто відсотки розраховуються і додаються до рахунку щомісяця. Щоб знайти місячну процентну ставку, ділимо річну ставку 1,2% на 12, оскільки в році 12 місяців: 1,2% /12 = 0,1%. Щомісяця ми будемо заробляти 0,1% відсотків. З цього, ми можемо встановити експоненціальну функцію, з нашою початковою сумою $1000 і темпом зростання\( r = 0.001\), і наш вхід\(m\) вимірюється в місяцях:\[f(m)=1000\left(1+\frac{0.012}{12}\right)^m=1000(1.001)^{m}\nonumber \]
Через 24 місяці рахунок виросте до\( f(24)=1000(1.001)^{24}\approx \$1024.28 \).
Вісмут-210 - це ізотоп, який радіоактивно розпадається приблизно на 13% щодня, тобто 13% решти Вісмут-210 перетворюється в інший атом (полоній-210 в даному випадку) щодня. Якщо почати з 100 мг вісмуту-210, скільки залишається через один тиждень?
Рішення
При радіоактивному розпаді замість кількості, що збільшується з відсотковою швидкістю, кількість зменшується з відсотковою швидкістю. Наша початкова кількість -\(a = 100\) мг, а наш темп зростання буде негативним 13%, оскільки ми зменшуємо:\( r = -0.13\). Це дає рівняння\[ Q(d)=100(1-0.13)^d=100(0.87)^d.\nonumber \] Це також можна пояснити визнанням того, що якщо 13% розпадається, то 87% залишається.
Через тиждень, 7 днів, кількість, що залишилася б\( Q(7)=100(0.87)^7=37.73 \) мг вісмуту-210 залишається.
\(T(q)\)являє собою загальну кількість контрактів на смартфони Android у тисячах, що проводяться певним регіоном магазину Verizon щоквартально з 1 січня 2010 року. Інтерпретуйте всі частини рівняння\( T(2)=86(1.64)^2=231.3056 \).
Рішення
Інтерпретуючи це з базової експоненціальної форми, ми знаємо, що 86 - це наша початкова цінність. Це означає, що 1 січня 2010 року цей регіон мав 86 000 контрактів на смартфони Android. Оскільки ми знаємо\(b = 1 + r = 1.64\), що з кожним кварталом кількість контрактів на смартфони зростає на 64%. \(T(2) = 231.3056\)означає, що у другому кварталі (або в кінці другого кварталу) було приблизно 231 305 контрактів на смартфони Android.
При роботі з експоненціальними показниками існує особлива константа, про яку ми повинні говорити. Це виникає, коли ми говоримо про речі, що постійно ростуть, такі як безперервне з'єднання, або природні явища, такі як радіоактивний розпад, які відбуваються безперервно.
\[e\approx 2.718282\nonumber \]
Оскільки часто\(e\) використовується як основа експоненціальної, більшість наукових та графічних калькуляторів мають кнопку, яка може обчислити потужності\(e\), як правило, позначені\(e^x\). Деякі комп'ютерні програми замість цього визначають функцію\(exp(x)\), де exp (x) =\(e^x\). Оскільки обчислення вивчає безперервні зміни, ми майже завжди будемо використовувати\(e\) засновану форму експоненціальних рівнянь у цьому курсі.
Безперервне зростання можна обчислити за формулою\[f(x)=ae^{rx}\nonumber \], де
- \(a\)це стартова сума,
- \(r\)це безперервний темп зростання.
Радон-222 розпадається з безперервною швидкістю 17,3% на добу. Скільки буде 100mg Radon-222 розпаду за 3 дні?
Рішення
Оскільки нам дається безперервна швидкість розпаду, ми використовуємо формулу безперервного зростання. Так як речовина розпадається, ми знаємо, що швидкість росту буде негативною:\(r = -0.173\),\( f(3)=100e^{-0.173(3)}\approx 59.512 \) мг Радона-222 залишиться.
Графіки експоненціальних функцій
Графічно, у функції\( f(x)=ab^x \).
- \(a\)є вертикальним перехопленням графіка.
- \(b\)визначає швидкість, з якою зростає графік:
- функція збільшиться\(b \gt 1\), якщо,
- функція зменшиться, якщо\(0 \lt b \lt 1\).
- Графік матиме горизонтальну асимптоту в\(y = 0\).
- Графік буде увігнутий вгору, якщо\(a \gt 0\); увігнутий вниз, якщо\(a \lt 0\).
- Доменом функції є всі дійсні числа.
- Діапазон дії функції дорівнює\( (0,\infty) \).
При замальовуванні графіка експоненціальної функції може бути корисно пам'ятати, що графік буде проходити через точки\((0, a)\) і\((1, ab)\).
Значення\(b\) визначатиме довгострокову поведінку функції:
- Якщо\(b \gt 1\), як\( x\to\infty \)\( f(x)\to\infty \), і як\( x\to -\infty \),\( f(x)\to 0 \).
- Якщо\(0 \lt b \lt 1\), як\( x\to\infty \)\( f(x)\to 0 \), і як\( x\to -\infty \),\( f(x)\to \infty \).
Намалюйте графік\( f(x)=4\left(\frac{1}{3}\right)^x \)
Рішення
Цей графік буде мати вертикальний перехоплення в (0,4), і проходити через точку\( \left(1,\frac{4}{3} \right) \). Так як\(b \lt 1\), графік буде зменшуватися до нуля. Так як\(a \gt 0\), графік буде увігнутий вгору.
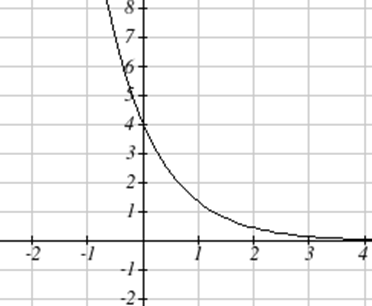
Ми також можемо бачити з графіка довгострокову поведінку: as\( x\to\infty \)\( f(x)\to 0 \), і as\( x\to -\infty \),\( f(x)\to \infty \).
Щоб краще відчути ефект\(a\) і\(b\) на графіку, вивчіть набори графіків нижче. Перший набір показує різні графіки, де\(a\) залишається незмінним і ми змінюємо тільки значення для\(b\). Зверніть увагу, що чим ближче значення\(b\) дорівнює 1, тим менш крутим буде графік.
У наступному наборі графіків,\(a\) змінюється і наше значення для\(b\) залишається колишнім.
Зверніть увагу, що зміна значення для a змінює вертикальний перехоплення. Так як\(a\) це множення\(b^x\) терміну,\(a\) діє як вертикальний коефіцієнт розтягування, а не як зсув. Зверніть увагу також, що довгострокова поведінка для всіх цих функцій однакова, оскільки фактор росту не змінився, і жодне з цих\(a\) значень не ввело вертикального перевороту.
Спробуйте самі за допомогою цього аплету:
Зіставте кожне рівняння з його графіком.
- \( f(x)=2(1.3)^x \)
- \( g(x)=2(1.8)^x \)
- \( h(x)=4(1.3)^x \)
- \( k(x)=4(0.7)^x \)
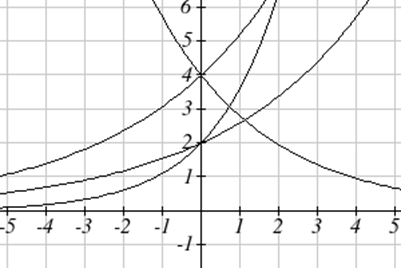
Рішення
Графік найбільш простий для ідентифікації, оскільки це єдине рівняння з коефіцієнтом росту менше одиниці, яке дасть спадний графік.\(k(x)\) Графік\(h(x)\) можна визначити як єдину зростаючу експоненціальну функцію з вертикальним перехопленням при (0,4). Графіки\(f(x)\) і\(g(x)\) обидва мають вертикальний перехоплення в (0,2), але оскільки\(g(x)\) має більший коефіцієнт росту, ми можемо визначити його як графік, що збільшується швидше.
