1.E: Огляд (вправи)
- Page ID
- 60324
1.1 Вправи
Кількість сміття\(G\), виробленого містом з населенням\(p\), дається по\(G = f(p)\). \(G\)вимірюється в тонни на тиждень, і\(p\) вимірюється тисячами людей.
- Місто Тола має населення 40 000 чоловік і виробляє 13 тонн сміття щотижня. Висловіть цю інформацію з точки зору функції\(f\).
- Поясніть сенс висловлювання\(f(5) = 2\).
Кількість кубічних ярдів бруду\(D\), необхідних для покриття саду площею\(a\) квадратних футів, задано\(D = g(a)\).
- Сад площею 5000\(ft^2\) вимагає 50 кубічних метрів бруду. Висловіть цю інформацію з точки зору функції\(g\).
- Поясніть сенс висловлювання\(g(100) = 1\).
Виберіть усі наведені нижче графіки, які представляються\(y\) як функція\(x\).
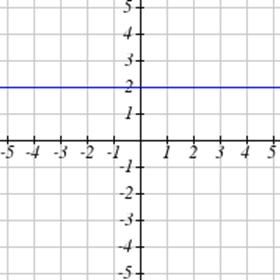
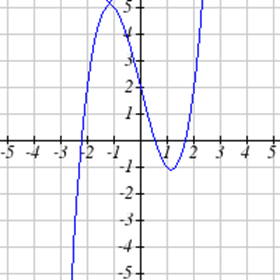
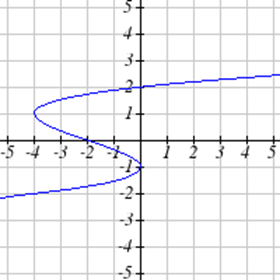
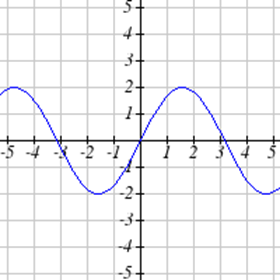
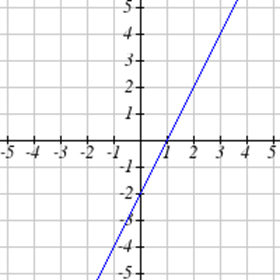
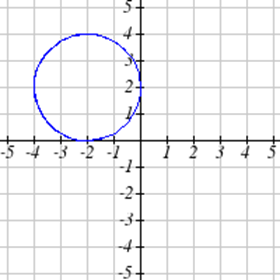
Виберіть усі наведені нижче графіки, які представляються\(y\) як функція\(x\).
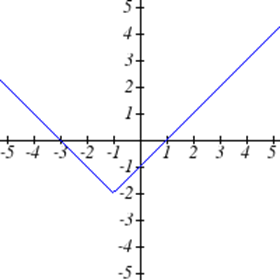
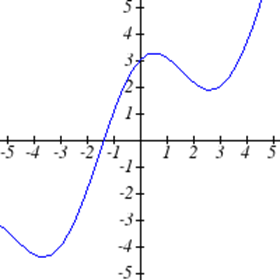
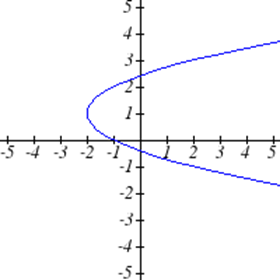
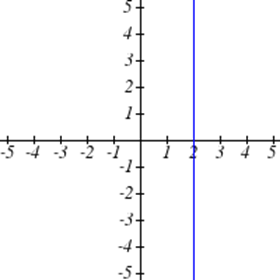
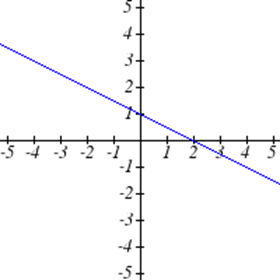
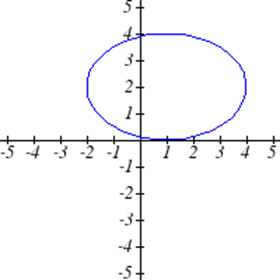
Виберіть всі наведені нижче таблиці, які представляються\(y\) як функція\(x\).
а.
|
х |
5 |
10 |
15 |
|
у |
3 |
8 |
14 |
б.
|
х |
5 |
10 |
15 |
|
у |
3 |
8 |
8 |
c.
|
х |
5 |
10 |
10 |
|
у |
3 |
8 |
14 |
Виберіть всі наведені нижче таблиці, які представляються\(y\) як функція\(x\).
а.
|
х |
2 |
6 |
13 |
|
у |
3 |
10 |
10 |
б.
|
х |
2 |
6 |
6 |
|
у |
3 |
10 |
14 |
c.
|
х |
2 |
6 |
13 |
|
у |
3 |
10 |
14 |
Враховуючи функцію\(g(x)\), наведену тут,
- Оцінити\(g(2)\)
- Вирішити\(g(x) = 2\)
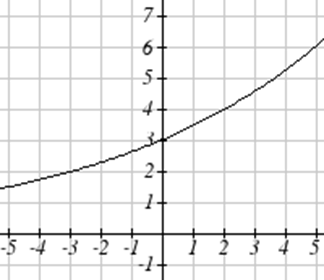
Дано функцію, наведену\(f(x)\) тут графіку.
- Оцінити\(f(4)\)
- Вирішити\(f(x) = 4\)
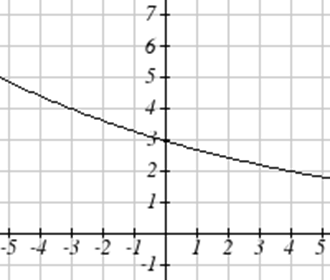
Виходячи з наведеної нижче таблиці,
- Оцінити\(f(3)\)
- Вирішити\(f(x) = 1\)
|
х |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
\(f(x)\) |
74 |
28 |
1 |
53 |
56 |
3 |
36 |
45 |
14 |
47 |
Виходячи з наведеної нижче таблиці,
- Оцінити\(f(8)\)
- Вирішити\(f(x) = 7\)
|
х |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
\(f(x)\) |
62 |
8 |
7 |
38 |
86 |
73 |
70 |
39 |
75 |
34 |
Для кожної з наступних функцій оцінюйте:\(f(-2)\),\(f(-1)\),\(f(0)\),\(f(1)\), і\(f(2)\)
| 11. \(f(x) = 4-2x\) | 12. \(f(x) = 8 - 3x\) |
| 13. \(f(x) = 8x^2 - 7x + 3\) | 14. \(f(x) = 6x^2 -7x+4\) |
| 15. \(f(x) = 3 + \sqrt{x+3}\) | 16. \(f(x) = 4 - \sqrt[3]{x-2}\) |
| 17. \(f(x) = \frac{x-3}{x+1}\) | 18. \(f(x) = \frac{x-2}{x+2}\) |
Нехай\(f(t) = 3t+5\)
- Оцінити\(f(0)\)
- Вирішити\(f(t) = 0\)
Нехай\(g(p) = 6 - 2p\)
- Оцінити\(g(0)\)
- Вирішити\(g(p) = 0\)
Використовуючи показаний графік,
- Оцінити\(f(c)\)
- Вирішити\(f(x) = p\)
- Які координати точок\(L\) і\(K\)?
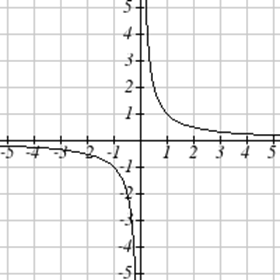
Зіставте кожен графік зі своїм рівнянням.
| а.\(y=x\) | б.\(y = x^3\) | \(y = \sqrt[3]{x}\) | д.\(y = \frac{1}{x}\) |
| е.\(y = x^2\) | ф.\(y = \sqrt{x}\) | г.\(y = |x|\) | ч.\(y = \frac{1}{x^2}\) |
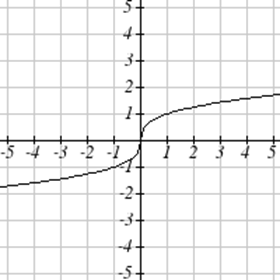
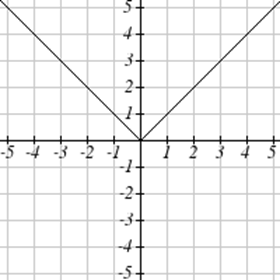
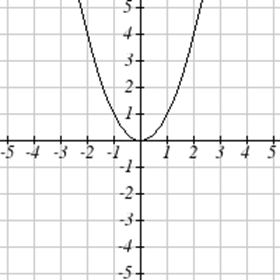
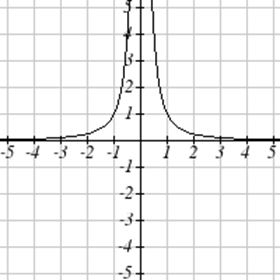
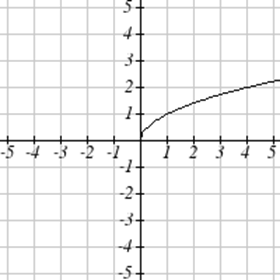
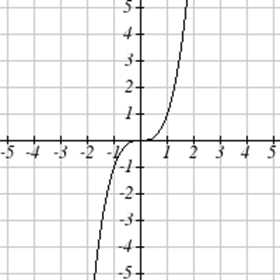
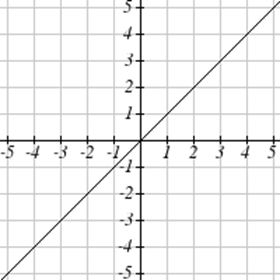
Для Вправ\(\PageIndex{23}-\PageIndex{24}\) запишіть область та діапазон кожного графіка як нерівність.
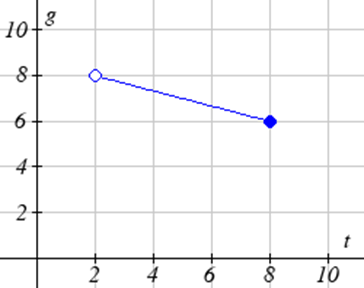
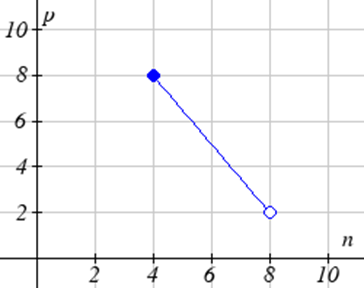
Знайдіть домен кожної функції.
| 25. \(f(x) = 3\sqrt{x-2}\) | 26. \(f(x) = 5\sqrt{x+3}\) |
| 27. \(f(x) = \frac{9}{x-6}\) | 28. \(f(x) = \frac{6}{x-8}\) |
| 29. \(f(x) = \frac{3x+1}{4x+2}\) | 30. \(f(x) = \frac{5x+3}{4x-1}\) |
1.2 Вправи
| 1. \(f(x) = 4x+8, g(x) = 7-x^2\) | 2. \(f(x) = 5x+7, g(x) = 4-2x^2\) |
| 3. \(f(x) = \sqrt{x+4}, g(x) = 12-x^3\) | 4. \(f(x) = \frac{1}{x+2}, g(x) = 4x+3\) |
|
х |
\(f(x)\) |
\(g(x)\) |
|
0 |
7 |
9 |
|
1 |
6 |
5 |
|
2 |
5 |
6 |
|
3 |
8 |
2 |
|
4 |
4 |
1 |
|
5 |
0 |
8 |
|
6 |
2 |
7 |
|
7 |
1 |
3 |
|
8 |
9 |
4 |
|
9 |
3 |
0 |
Використовуйте таблицю значень для оцінки кожного виразу.
| 5. \(f(g(8))\) |
| 6. \(f(g(5))\) |
| 7. \(g(f(5))\) |
| 8. \(g(f(3))\) |
| 9. \(f(f(4))\) |
| 10. \(f(f(1))\) |
| 11. \(g(g(2))\) |
| 12. \(g(g(6))\) |
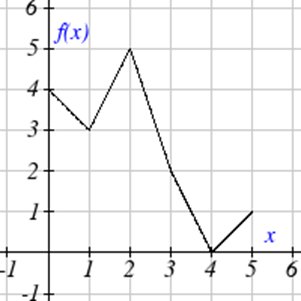
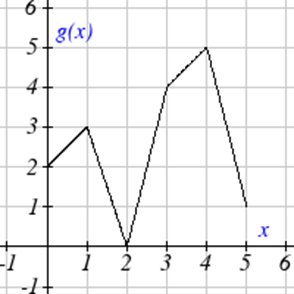
Використовуйте графіки для оцінки виразів нижче.
| 13. \(f(g(3))\) |
| 14. \(f(g(1))\) |
| 15. \(g(f(1))\) |
| 16. \(g(f(0))\) |
| 17. \(f(f(5))\) |
| 18. \(f(f(4))\) |
| 19. \(g(g(2))\) |
| 20. \(g(g(0))\) |
Для кожної пари функцій знайдіть\(f(g(x))\) і\(g(f(x))\). Спростіть свої відповіді.
| 21. \(f(x) = \frac{1}{x-6}, g(x) = \frac{7}{x}+6\) | 22. \(f(x) = \frac{1}{x-4}, g(x) = \frac{2}{x} + 4\) |
| 23. \(f(x) = x^2+1, g(x) = \sqrt{x+2}\) | 24. \(f(x) = \sqrt{x} + 2, g(x) = x^2 + 3\) |
| 25. \(f(x) = |x|, g(x) = 5x+1\) | 26. \(f(x) = \sqrt[3]{x}, g(x) = \frac{x+1}{x^3}\) |
Якщо\(f(x) = x^4+6\)\(g(x) = x - 6\), і\(h(x) = \sqrt{x}\), знайти\(f(g(h(x)))\)
Якщо\(f(x) = x^2+1\)\(g(x) = \frac{1}{x}\), і\(h(x) = x+3\), знайти\(f(g(h(x)))\)
Функція\(D(p)\) видає кількість предметів, які будуть затребувані, коли ціна є\(p\). Виробнича собівартість,\(C(x)\) це витрати на виробництво\(x\) виробів. Щоб визначити собівартість продукції, коли ціна становить 6 доларів, ви б зробили, що з наступного:
- Оцінити\(D(C(6))\)
- Вирішити\(C(D(6))\)
- Оцінити\(D(C(x)) = 6\)
- Вирішити\(C(D(p)) = 6\)
Функція\(A(d)\) дає рівень болю за шкалою 0-10, яку відчуває пацієнт з\(d\) міліграмами препарату для зменшення болю в своїй системі. Міліграми препарату в системі пацієнта через\(t\) хвилини моделюється\(m(t)\). Щоб визначити, коли пацієнт буде знаходитися на рівні болю 4, потрібно:
- Оцінити\(A(m(4))\)
- Вирішити\(m(A(4))\)
- Оцінити\(A(m(t)) = 4\)
- Вирішити\(m(A(d)) = 4\)
Знайти функції\(f(x)\) і\(g(x)\) тому задана функція може бути виражена як\(h(x) = f(g(x))\).
| 31. \(h(x) = (x+2)^2\) | 32. \(h(x) = (x-5)^3\) |
| 33. \(h(x) = \frac{3}{x-5}\) | 34. \(h(x) = \frac{4}{(x+2)^2}\) |
| 35. \(h(x) = 3+\sqrt{x-2}\) | 36. \(h(x) = 4+\sqrt[3]{x}\) |
Намалюйте графік кожної функції як перетворення функції інструментарію.
| 37. \(f(t) = (t+1)^2 - 3\) | 38. \(h(x) = |x-1|+4\) |
| 39. \(k(x) =(x-2)^3 -1\) | 40. \(m(t) = 3+\sqrt{t+2}\) |
| 41. \(f(x) = 4(x+1)^2 - 5\) | 42. \(g(x) = 5(x+3)^2 - 2\) |
| 43. \(h(x) = -2|x-4|+3\) | 44. \(k(x) = -3\sqrt{x} - 1\) |
Напишіть рівняння для кожної функції, наведеної нижче.
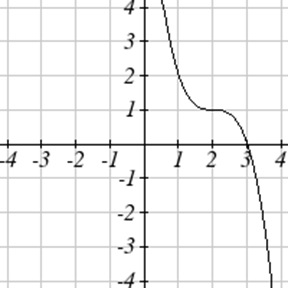
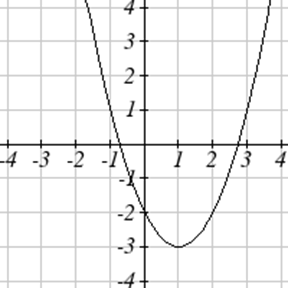
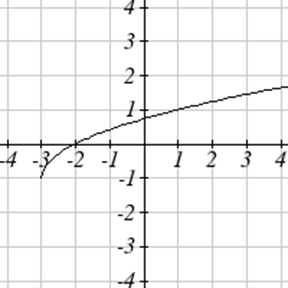
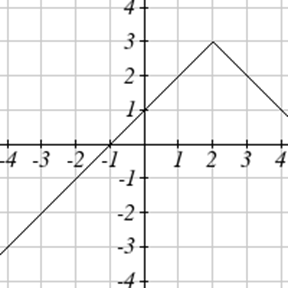
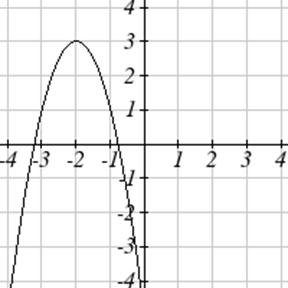
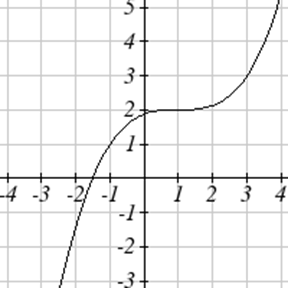
Для кожної графічної функції оцініть інтервали, на яких функція збільшується і зменшується.
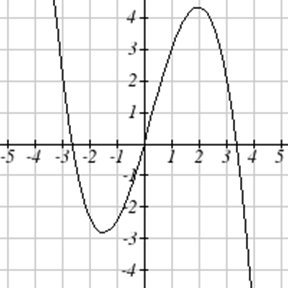
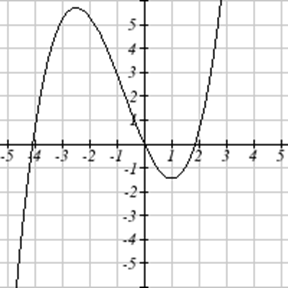 52.
52.1.3 Вправи
Населення міста зростає лінійно. У 2003 році чисельність населення становила 45 000, а населення щорічно зростає на 1700 чоловік. Напишіть рівняння\(P(t)\), для населення\(t\) років після 2003 року.
Населення міста зростає лінійно. У 2005 році населення становило 69 000, а населення щорічно зростає на 2500 чоловік. Напишіть рівняння\(P(t)\), для населення\(t\) років після 2005 року.
Тіммі йде на ярмарок з 40 доларів. Кожна поїздка коштує 2 долари. Скільки грошей у нього залишиться після катання на\(n\) атракціоні?
Опівдні бариста помічає, що у неї 20 доларів у банку для наконечників. Якщо вона робить в середньому $0.50 від кожного клієнта, скільки вона матиме в банку для наконечників, якщо вона обслуговує\(n\) більше клієнтів під час своєї зміни?
Телефонна компанія стягує плату за обслуговування за формулою:\(C(n) = 24+0.1n\), де кількість хвилин\(n\) розмовляють, і\(C(n)\) щомісячна плата, в доларах.
Знайти і інтерпретувати швидкість зміни і початкове значення.
Телефонна компанія стягує плату за обслуговування за формулою:\(C(n) = 26+0.04n\), де кількість хвилин\(n\) розмовляють, і\(C(n)\) щомісячна плата, в доларах.
Знайти і інтерпретувати швидкість зміни і початкове значення.
З урахуванням кожного набору інформації знайдіть лінійне рівняння, що задовольняє умовам, якщо це можливо.
| 7. \(f(-5) = -4\), і\(f(5)=2\) | 8. \(f(-1)=4\), і\(f(5)=1\) |
| 9. Проходить через (2,4) і (4,10) | 10. Проходить через (1, 5) і (4, 11) |
| 11. Проходить через (-1,4) і (5, 2) | 12. Проходить через (-2, 8) і (4, 6) |
| 13. \(x\)перехопити в (-2, 0) і\(y\) перехопити в (0, -3) | 14. \(x\)перехопити в (-5, 0) і\(y\) перехопити в (0, 4) |
Знайдіть рівняння для графічної функції.
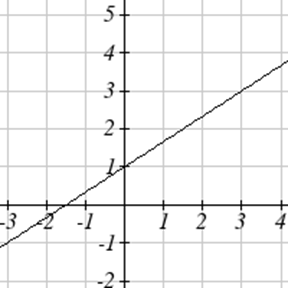
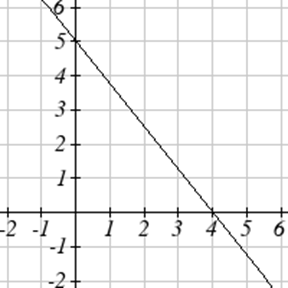
Одяг бізнес знаходить, що існує лінійна залежність між кількістю сорочок\(n\), вона може продати і ціною\(p\), вона може стягувати плату за сорочку. Зокрема, історичні дані показують, що 1000 сорочок можна продати за ціною 30 доларів, тоді як 3000 сорочок можна продати за ціною 22 долари. Знайдіть лінійне рівняння у формі\(p=mn+b\), яка дає ціну, яку\(p\) вони можуть стягувати за\(n\) сорочки.
Фермер виявляє, що існує лінійна залежність між кількістю стебел квасолі\(n\), вона садить і врожайністю\(y\), яку виробляє кожна рослина. Коли вона висаджує 30 стебел, кожна рослина дає 30 унцій бобів. Коли вона висаджує 34 стебла, кожна рослина виробляє 28 унцій бобів. Знайдіть лінійні залежності в\(y=mn+b\) тому вигляді, який дає урожай при\(n\) посадці стебел.
Зіставте кожне лінійне рівняння з його графіком
| 19. \(f(x) = -x-1\) |
| 20. \(f(x) = -2x-1\) |
| 21. \(f(x) = -\frac{1}{2}x-1\) |
| 22. \(f(x) = 2\) |
| 23. \(f(x) = 2+x\) |
| 24. \(f(x) = 3x+2\) |
Намалюйте графік кожного рівняння
| 25. \(f(x) = -2x-1\) | 26. \(g(x) = -3x+2\) |
| 27. \(h(x)=\frac{1}{3}x+2\) | 28. \(k(x) = \frac{2}{3}x-3\) |
Знайти точку, в якій пряма\(f(x) = -2x-1\) перетинає пряму\(g(x)=-x\)
Знайти точку, в якій пряма\(f(x)=2x+5\) перетинає пряму\(g(x)=-3x-5\)
Компанія з прокату автомобілів пропонує два плани оренди автомобіля.
План А: 30 доларів на день і 18 центів за милю
План Б: 50 доларів на добу з безкоштовним необмеженим пробігом
Скільки миль вам потрібно було б проїхати для плану B, щоб заощадити ваші гроші?
Компанія стільникових телефонів пропонує два варіанти даних для своїх передплачених телефонів
Оплата за використання: $0.002 за кілобайт (KB) використано
Пакет даних: $5 за 5 Мегабайт (5120 Кілобайт) + $0.002 за додавання КБ
Припускаючи, що ви будете використовувати менше 5 мегабайт, за яких обставин пакет даних заощадить вам гроші?
Федеральний гелієвий резерв утримував близько 16 мільярдів кубічних футів гелію в 2010 році, і щороку виснажується приблизно на 2,1 мільярда кубічних футів.
- Дайте лінійне рівняння для решти федеральних запасів гелію\(R\), в\(t\) перерахунку на кількість років з 2010 року.
- У 2015 році якими будуть запаси гелію?
- Якщо швидкість виснаження не зміниться, коли буде виснажений Федеральний гелієвий резерв?
Припустимо, поточні світові запаси нафти становлять 1820 млрд барелів. Якщо в середньому загальні запаси зменшуються на 25 млрд барелів нафти щороку:
- Дайте лінійне рівняння для решти запасів нафти\(R\), в\(t\) перерахунку на кількість років, відтепер.
- Через сім років, якими будуть запаси нафти?
- Якщо темпи виснаження не зміняться, коли будуть виснажені світові запаси нафти?
1.4 Вправи
Спрощення кожного виразу
| 1. \(x^3x^5\) | 2. \(x^4x^2\) |
| 3. \(\left(x^3\right)^4\) | 4. \(\left(x^7\right)^2\) |
| 5. \(\left(2x^2\right)^3x^4\) | 6. \(\left(5x^4\right)^2x^5\) |
| 7. \(\frac{\left(3x^2\right)^2}{6x^3}\) | 8. \(\frac{5x\left(4x\right)^2}{2x^2}\) |
Спрощення та переписування без негативних показників
| 9. \(4x^{-3}\) | 10. \(2x^{-5}\) |
| 11. \(x^{-4}x^2\) | 12. \(x^{-2}x\) |
| 13. \(\frac{5x^{-3}}{2x^{-6}}\) | 14. \(\frac{2x^{-4}}{6x^{-2}}\) |
Перепишіть з використанням негативних або дробових показників
| 15. \(\frac{4}{x^{-5}}\) | 16. \(\frac{4}{x^{-3}}\) |
| 17. \(3\sqrt{x}\) | 18. \(\sqrt[4]{x}\) |
| 19. \(\frac{4}{\sqrt[3]{x}}\) | 20. \(\frac{1}{5\sqrt{x}}\) |
Перепишіть як радикал
| 21. \(4x^{-\frac{1}{2}}\) | 22. \(5x^{-\frac{1}{3}}\) |
| 23. \(2x^{\frac{1}{3}}\) | 24. \(5x^{\frac{3}{2}}\) |
1.5 Вправи
Напишіть рівняння для квадратичної функції з графіком.
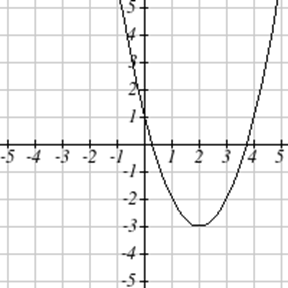
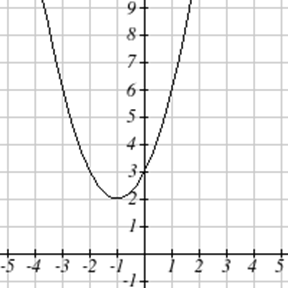
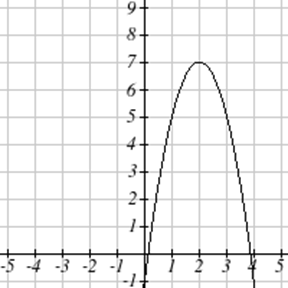
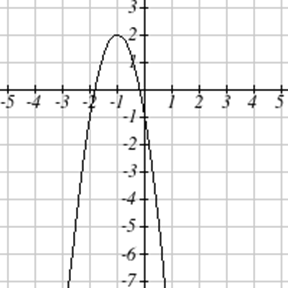
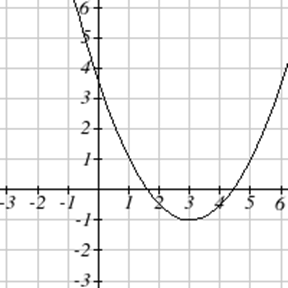
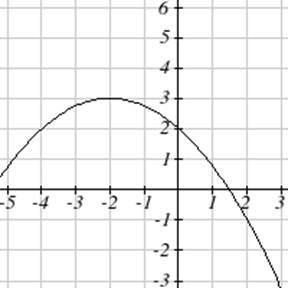
| 7. \(y(x) = 2x^2+10x+12\) | 8. \(z(p)=3x^2+6x-9\) |
| 9. \(f(x)=2x^2-10x+4\) | 10. \(g(x) = -2x^2-14x+12\) |
| 11. \(h(t)=-4t^2+6t-1\) | 12. \(k(t) = 2x^2+4x-15\) |
Висота кинутого в повітря кулі задається тим\(h(x) = -\frac{1}{12}x^2+6x+3\), де\(x\) горизонтальна відстань в футах від точки, в яку кидається м'яч.
- Наскільки високий м'яч, коли його кинули?
- Яка максимальна висота кулі?
- Як далеко від метальника м'яч б'є об землю?
У повітря кидається списа. Її висота задається тим\(h(x)=-\frac{1}{20}x^2+8x+6\), де\(x\) горизонтальне відстань в футах від точки, в яку закидається списа.
- Наскільки високо знаходиться списа, коли його кидали?
- Яка максимальна висота списа?
- Як далеко від метальника спис б'є об землю?
1.6 Вправи
Знайти ступінь і провідний коефіцієнт кожного полінома
| 1. \(4x^7\) | 2. \(5x^6\) |
| 3. \(5-x^2\) | 4. \(6+3x-4x^3\) |
| 5. \(-2x^4-3x^2+x-1\) | 6. \(6x^5-2x^4+x^2+3\) |
Знайдіть вертикальні та горизонтальні перехоплення кожної функції.
| 7. \(f(t) = 2(t-1)(t+2)(t-3)\) | 8. \(f(x)=3(x+1)(x-4)(x+5)\) |
| 9. \(g(n) = -2(3n-1)(2n+1)\) | 10. \(k(u)=-3(4-n)(4n+3)\) |
| 11. \(C(t) = 2t^4-8t^3+6t^2\) | 12. \(C(t)=4t^4+12t^3-40t^2\) |
Використовуйте калькулятор або іншу графічну технологію, щоб графічно вирішити нулі функції.
| 13. \(f(x) = x^3 - 7x^2+4x+30\) | 14. \(g(x)=x^3-6x^2+x+28\) |
Вирішити кожну нерівність.
| 15. \((x-3)(x-2)^2>0\) | 16. \((x-5)(x+1)^2>0\) |
| 17. \((x-1)(x+2)(x-3)<0\) | 18. \((x-4)(x+3)(x+6)<0\) |
Для кожної функції знайдіть горизонтальні перехоплення, вертикальні перехоплення, вертикальні асимптоти та горизонтальну асимптоту.
| 19. \(p(x) = \frac{2x-3}{x+4}\) | 20. \(q(x) = \frac{x-5}{3x-1}\) |
| 21. \(s(x) = \frac{4}{(x-2)^2}\) | 22. \(r(x) = \frac{5}{(x+1)^2}\) |
| 23. \(f(x) = \frac{3x^2-14x-5}{3x^2+8x-16}\) | 24. \(g(x) = \frac{2x^2+7x-15}{3x^2-14+15}\) |
| 25. \(h(x) = \frac{2x^2+x-1}{x-4}\) | 26. \(k(x) = \frac{2x^2-3x-20}{x-5}\) |
У вченого є стакан, що містить 20 мл розчину, що містить 20% кислоти. Щоб розбавити це, вона додає чисту воду.
- Напишіть рівняння концентрації в склянці після додавання\(n\) мл води.
- Знайдіть концентрацію, якщо було додано 10 мл води.
- Скільки мл води необхідно додати, щоб отримати 4% розчин?
- Що таке поведінка\(n \to \infty\), і яке фізичне значення цього?
У вченого є стакан, що містить 30 мл розчину, що містить 3 грами гідроксиду калію. Для цього вона змішує розчин, що містить 8 міліграм на мл гідроксиду калію.
- Напишіть рівняння концентрації в баку після додавання\(n\) мл другого розчину.
- Знайдіть концентрацію, якщо було додано 10 мл другого розчину.
- Скільки мл води необхідно додати, щоб отримати 50 мг/мл розчину?
- Що таке поведінка\(n \to \infty\), і яке фізичне значення цього?
1.7 Вправи
Популяція налічує 11 000 організмів спочатку і зростає на 8,5% щороку. Напишіть експоненціальну модель для населення.
Населення в даний час становить 6000 і зростає на 1,2% щодня. Напишіть експоненціальну модель для населення.
Автомобіль, придбаний за 32 500 доларів, знецінюється за постійною ставкою 5% щороку. Визначте приблизну вартість транспортного засобу через 12 років після покупки.
Бізнес купує $125 000 офісних меблів, які знецінюються з постійною ставкою 12% щороку. Знайти залишкову вартість меблів через 6 років після покупки.
Якщо 4000 доларів інвестуються на банківський рахунок під процентну ставку 7 відсотків на рік, знайдіть суму в банку через 9 років, якщо відсотки збільшуються щорічно, щоквартально, щомісяця та безперервно.
Якщо 6000 доларів інвестуються на банківський рахунок за процентною ставкою 9 відсотків на рік, знайдіть суму в банку через 5 років, якщо відсотки збільшуються щорічно, щоквартально, щомісяця та безперервно.
Зіставте кожну функцію за допомогою одного з наведених нижче графіків.
| 7. \(f(x) = 2(0.69)^x\) |
| 8. \(f(x) = 2(1.28)^x\) |
| 9. \(f(x) = 2(0.81)^x\) |
| 10\(f(x) = 4(1.28)^x\) |
| 11. \(f(x) = 2(1.59)^x\) |
| 12. \(f(x) = 4(0.69)^x\) |
Якщо всі графи праворуч мають рівняння з формою\(f(t) = ae^{kt}\),
|
13. Який графік має найбільше значення\(k\)? |
|
14. Який графік має найменше значення\(k\)? |
|
15. Який графік має найбільше значення\(a\)? |
|
16. Який графік має найменше значення\(a\)? |
1.8 Вправи
Перепишіть кожне рівняння в експоненціальній формі
| 1. \(\log (v) = t\) | 2. \(\log (r) = s\) | 3. \(\ln (w) = n\) | 4. \(\ln (x) = y\) |
Перепишіть кожне рівняння в логарифмічній формі.
| 5. \(10^a = b\) | 6. \(10^p = v\) | 7. \(e^k = h\) | 8. \(e^y = x\) |
Розв'яжіть кожне рівняння для змінної.
| 9. \(5^{x} = 14\) | 10. \(3^x = 23\) | 11. \(7^x = \frac{1}{15}\) | 12. \(3^x = \frac{1}{4}\) |
| 13. \(e^{5x} = 17\) | 14. \(e^{3x} = 12\) | 15. \(3^{4x-5} = 38\) | 16. \(4^{2x-3} = 44\) |
| 17. \(1000(1.03)^t = 5000\) | 18. \(200(1.06)^t = 550\) |
| 19. \(3(1.04)^{3t} = 8\) | 20. \(2(1.08)^{4t} = 7\) |
| 21. \(50e^{-0.12t} = 10\) | 22. \(10e^{-0.03t} = 4\) |
| 23. \(10 - 8 \left(\frac{1}{2}\right)^x = 5\) | 24. \(100-100\left(\frac{1}{4}\right)^x = 70\) |
Населення Кенії становило 39,8 мільйона в 2009 році і щорічно зростає приблизно на 2,6%. Якщо ця тенденція збережеться, коли населення перевищить 45 мільйонів?
Населення Алжиру становило 34,9 мільйона в 2009 році і щорічно зростає приблизно на 1,5%. Якщо ця тенденція збережеться, коли населення перевищить 45 мільйонів?
Якщо 1000 доларів інвестується в рахунок, який заробляє 3% щомісяця, як довго він буде приймати рахунок, щоб вирости в ціні до 1500 доларів?
Якщо 1000 доларів інвестується в рахунок, який заробляє 2% щоквартально, як довго він буде приймати рахунок, щоб вирости в ціні до $1300?
Намалюйте графік:\(f(x) = \log (x)\),\(g(x) = \ln (x)\)
Знайдіть домен кожної функції.
| 30. \(f(x) = \log (x-5)\) | 31. \(f(x) = \ln (3-x)\) |
| 32. \(f(x) = \ln (1-3x)\) | 33. \(f(x) = \log (2x+5)\) |
