1.3: Лінійні функції
- Page ID
- 60356
Коли ви заїжджаєте в таксі в Аллентауні, лічильник негайно прочитає $3.30; це «падіння» заряду, зроблене при активації таксометра. Після цього початкового внеску таксометр додасть $2.40 за кожну милю, яку проїжджає таксі. У цьому випадку загальна вартість проїзду на таксі залежить від кількості миль, пройдених у таксі, і ми можемо запитати, чи можна моделювати цей тип сценарію за допомогою функції. Використовуючи описові змінні, ми вибираємо\(m\) для миль і\(C\) для Вартість в доларах в залежності від миль:\(C(m)\).
Ми точно знаємо\(C(0)=3.30\), що, оскільки плата за падіння в розмірі 3.30 доларів оцінюється незалежно від того, скільки миль проїхали. Оскільки $2.40 додається за кожну милю керованої, ми могли б написати, що якщо\(m\) милі рухаються,\(C(m)=3.30+2.40m\) тому що ми починаємо з $3.30 падіння плати, а потім за кожну милю збільшення ми додаємо $2.40.
Добре переконатися, що одиниці мають сенс у цьому рівнянні. Заряд за падіння $3.30 вимірюється в доларах; $2.40 заряд вимірюється в доларах за милю. Отже,\[C(m)=3.30\text{ dollars}+\left(2.40\frac{\text{dollars}}{\text{mile}}\right) (m\text{ miles})\nonumber \] коли долари за милю множаться на кількість миль, результатом є кількість доларів, що відповідають одиницям на 3.30, і відповідність потрібних одиниць для\(C\) функції.
Зверніть увагу, що це рівняння\(C(m)=3.30+2.40m\) складалося з двох величин. Перший - фіксований заряд $3.30, який не змінюється залежно від значення вхідного сигналу. Другий - це $2.40 доларів за милю значення, що є швидкістю зміни. У рівнянні ця швидкість зміни множиться на вхідне значення.
Дивлячись на цю саму проблему у форматі таблиці, ми також можемо побачити зміни вартості на 2,40 долара за кожне збільшення 1 милі:
| \(m\) | 0 | 1 | 2 | 3 |
| \(C(m)\) | 3.30 | 5.70 | 8.10 | 10.50 |
Тут важливо відзначити, що в цьому рівнянні швидкість зміни постійна; протягом будь-якого інтервалу швидкість зміни однакова.
Графікуючи це рівняння,\(C(m)=3.30+2.40m\) ми бачимо, що форма є лінією, саме так ці функції отримують свою назву: лінійні функції.
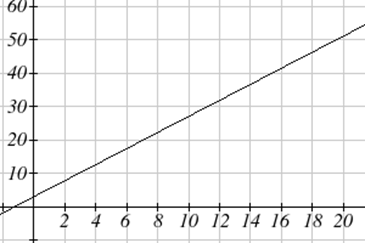
Коли кількість миль дорівнює нулю, вартість становить $3.30, даючи точку (0, 3,30) на графіку. Це вертикаль або\(C(m)\) перехоплення. Графік збільшується по прямій лінії зліва направо, оскільки для кожної милі вартість зростає на $2.40; ця ставка залишається послідовною.
Лінійна функція - це функція, графік якої створює лінію. Лінійні функції завжди можуть бути записані у вигляді\[f(x)=b+mx\nonumber \] або\[f(x)=mx+b\nonumber \] де\(b\) знаходиться початкове або початкове значення функції (з введенням\(x = 0\)), і\(m\) є постійною швидкістю зміни функції.
Така форма лінії називається ухилом-перехопленням формою лінії.
Багато людей люблять писати лінійні функції у формі,\(f(x)=b+mx\) оскільки це відповідає тому, як ми схильні говорити: «Вихід починається\(b\) і збільшується зі швидкістю»\(m\).
Тільки з цієї причини ми будемо використовувати\(f(x)=b+mx\) форму для багатьох прикладів, але пам'ятайте, що вони еквівалентні і можуть бути написані правильно обома способами. [Хоча це конвенція книги, в класі та у відео, які я, швидше за все, використовую\(f(x)=mx+b\).]
\(m\)- постійна швидкість зміни функції (також називається нахилом). Нахил визначає, чи є функція зростаючою або спадною функцією.
- \(f(x)=b+mx\)є зростаючою функцією, якщо\(m\gt 0\).
- \(f(x)=b+mx\)є спадною функцією if\(m\lt 0\).
Якщо\(m=0\), швидкість зміни дорівнює 0, а функція -\(f(x)=b+0x=b\) це всього лише горизонтальна лінія, що проходить через точку (0, б), ні збільшуючи, ні зменшуючи.
Маркус в даний час володіє 200 піснями у своїй колекції iTunes. Щомісяця він додає 15 нових пісень. Напишіть формулу для кількості пісень\(N\), в своїй колекції iTunes в залежності від кількості місяців,\(m\). Скільки пісень він буде володіти за рік?
Рішення
Початкове значення для цієї функції дорівнює 200, так як він в даний час володіє 200 піснями, так що\(N(0)=200\). Кількість пісень збільшується на 15 пісень на місяць, тому швидкість зміни становить 15 пісень на місяць. За допомогою цієї інформації ми можемо написати формулу:\[N(m)=200+15m.\nonumber \]
\(N(m)\)є зростаючою лінійною функцією.
За допомогою цієї формули ми можемо передбачити, скільки пісень у нього буде за 1 рік (12 місяців):\[N(12)=200+15(12)=200+180=380.\nonumber \] Маркус матиме 380 пісень за 12 місяців.
Задано два значення для вхідних даних\( x_2 \),\( x_1 \) і, і два відповідних значення для виходу\( y_2 \),\( y_1 \) і, або набір точок,\( (x_1,y_1) \) і\( (x_2,y_2) \), якщо ми хочемо знайти лінійну функцію, яка містить обидві точки, ми можемо обчислити швидкість зміни,\(m\):\[m=\dfrac{\text{change in output}}{\text{change in input}}=\dfrac{\Delta y}{\Delta x}=\dfrac{y_2-y_1}{x_2-x_1}.\nonumber \]
Швидкість зміни лінійної функції також називається нахилом лінії.
Примітка в позначенні функції,\(y_1=f(x_1)\) і\(y_2=f(x_2)\), так що ми могли б еквівалентно написати\[m=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}.\nonumber \]
Населення міста збільшилося з 23 400 до 27 800 в період з 2002 по 2006 рік. Знайти швидкість зміни популяції за цей часовий проміжок.
Рішення
Швидкість змін буде співвідносити зміну чисельності населення зі зміною в часі. Чисельність населення збільшилася на 27800-23400=4400 осіб за 4-річний часовий проміжок. Щоб дізнатися швидкість зміни, кількість людей в рік населення змінилося на:\[\dfrac{4400 \text{ people}}{4\text{ years}}=1100\dfrac{\text{people}}{\text{year}}=1100 \text{ people per year}.\nonumber \]
Зверніть увагу, що ми знали, що населення збільшується, тому ми очікуємо, що наша цінність буде\(m\) позитивною. Це швидкий спосіб перевірити, чи є ваша цінність розумною.
Тиск\(P\), в фунтах на квадратний дюйм (PSI) на дайвер залежить від їх глибини нижче поверхні води, в футах\(d\), дотримуючись рівняння\(P(d)=14.696+0.43d\). Інтерпретувати компоненти цієї функції.
Рішення
Швидкість зміни, або нахил, 0.434 матиме одиниці\(\dfrac{\text{output}}{\text{input}}=\dfrac{\text{pressure}}{\text{depth}}=\dfrac{\text{PSI}}{\text{ft}}\). Це говорить нам про те, що тиск на дайвера збільшується на 0.434 PSI для кожної ноги їх глибина збільшується.
Початкове значення, 14.696, матиме ті ж одиниці, що і вихід, тому це говорить нам про те, що на глибині 0 футів тиск на дайвера становитиме 14.696 PSI.
Тепер ми можемо знайти швидкість зміни, задану двома парами вхід-виводу, і могли б написати рівняння для лінійної функції, якби ми мали швидкість зміни та початкове значення. Якщо у нас є дві пари введення-виведення і вони не включають початкове значення функції, то нам доведеться вирішити для неї.
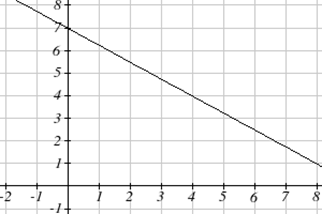
Напишіть рівняння для лінійної функції, наведеної нижче.
Рішення
Дивлячись на графік, ми можемо помітити, що він проходить через точки (0, 7) і (4, 4). З першого значення ми знаємо початкове значення функції є\(b = 7\), тому в цьому випадку нам потрібно буде тільки обчислити швидкість зміни:\[m=\dfrac{4-7}{4-0}=\dfrac{-3}{4}\nonumber \]
Це дозволяє нам записати рівняння:\[f(x)=7-\frac{3}{4}x\nonumber \]
Якщо\(f(x)\) є лінійною функцією\(f(3)=-2\), і\(f(8)=1\), знайдіть рівняння для функції.
Рішення
У\(\PageIndex{3}\) прикладі ми обчислили швидкість зміни бути\(m=\frac{3}{5}\). У цьому випадку ми не знаємо початкового значення\(f(0)\), тому доведеться вирішувати його. Використовуючи швидкість зміни, ми знаємо, що рівняння матиме вигляд\(f(x)=b+\frac{3}{5}x\). Оскільки ми знаємо значення функції коли\(x = 3\), ми можемо оцінити функцію на 3:\(f(x)=b+\frac{3}{5}(3)\).
Оскільки ми це знаємо\(f(3)=-2\), ми можемо замінити з лівого боку:\(-2=b+\frac{3}{5}(3)\).
Це залишає нам рівняння, яке ми можемо вирішити для початкового значення:\(b=-2-\frac{9}{5}=-\frac{19}{5}\).
Поєднуючи це зі значенням швидкості зміни, ми тепер можемо написати формулу для цієї функції:\[f(x)=-\frac{19}{5}+\frac{3}{5}x.\nonumber \]
В якості альтернативи підходу, використаному вище для пошуку початкового значення, b, ми можемо використовувати точку-нахил форми лінії замість.
Рівняння для прямої, що проходить через точку\((x_1, y_1)\) з нахилом,\(m\) можна записати як\[y-y_1=m(x-x_1)\nonumber \]
Це називається точково-похилою формою лінії. Це трохи простіше писати, якщо ви знаєте точку і нахил, але вимагає трохи роботи, щоб переписати в форму нахилу-перехоплення, і вимагає запам'ятовування іншої формули.
Працюючи продавцем страхування, Ілля заробляє базову зарплату і комісію за кожним новим полісом, тому тижневий дохід Іллі\(I\), залежить від кількості нових полісів, п, який він продає протягом тижня. Минулого тижня він продав 3 нових поліса, а за тиждень заробив 760 доларів. За тиждень до цього він продав 5 нових полісів, і заробив 920 доларів. Знайдіть рівняння для\(I(n)\), і інтерпретуйте значення компонентів рівняння.
Рішення
Дана інформація дає нам дві пари вхід-вихід: (3,760) і (5920). Почнемо з пошуку швидкості змін:\[m=\dfrac{920-760}{5-3}=\dfrac{160}{2}=80.\nonumber \]
Відстеження одиниць може допомогти нам інтерпретувати цю кількість. Дохід збільшився на 160 доларів, коли кількість полісів збільшилася на 2, тому швидкість зміни становить 80 доларів за поліс; Ілля заробляє комісію в розмірі 80 доларів за кожен проданий протягом тижня поліс.
Тепер ми можемо записати рівняння, використовуючи точку-нахил форми лінії, використовуючи тільки що знайдений нахил і точку (3,760):\[I-760= 80(n-3)\nonumber \]
Якби ми хотіли це у формі функції (форма перехоплення нахилу), ми могли б переписати рівняння в таку форму:\[\begin{align*} I-760 & = 80(n-3)\\ I-760 & = 80n-240\\ I(n) & = 520+80n \end{align*}\]
Ця форма дозволяє побачити початкове значення функції: 520. Це дохід Іллі коли\(n = 0\), а значить, нові поліси не продаються. Ми можемо трактувати це як базову зарплату Іллі за тиждень, яка не залежить від кількості проданих полісів.
Наша остаточна інтерпретація: базова зарплата Іллі становить 520 доларів на тиждень, і він заробляє додаткову комісію в розмірі 80 доларів за кожен продаваний поліс щотижня.
Графіки лінійних функцій
Графічно, в рівнянні\(f(x)=b+mx\),
- \(b\)це вертикальний перехоплення графіка і говорить нам, що ми можемо почати наш графік на\((0, b)\)
- і\(m\) є нахилом лінії і говорить нам, як далеко підніматися і бігти, щоб дістатися до наступної точки.
Як тільки у нас є принаймні 2 точки, ми можемо розширити графік лінії вліво і вправо.
Графік\(f(x)=5-\frac{2}{3}x\) за допомогою вертикального перехоплення і нахилу.
Рішення
Вертикальний перехоплення функції дорівнює (0, 5), даючи нам точку на графіку прямої. Ухил є\(-\frac{2}{3}\). Це говорить нам про те, що на кожні 3 одиниці графік «біжить» по горизонталі, вертикальний «підйом» зменшується на 2 одиниці. У графіках ми можемо використовувати це, спочатку побудувавши наш вертикальний перехоплення на графіку, а потім за допомогою нахилу, щоб знайти другу точку. Від початкового значення (0, 5) нахил говорить нам, що якщо ми рухатимемося вправо 3, ми будемо рухатися вниз 2, перемістивши нас до точки (3, 3). Ми можемо продовжити це знову, щоб знайти третю точку в (6, 1). Нарешті, продовжити лінію вліво і вправо, що містить ці точки.
Іншим варіантом графічного оформлення є використання перетворень функції ідентичності\(f(x)=x\). У\(f(x)=mx\) рівнянні\(m\) діє як вертикальна розтяжка функції ідентичності. Коли\(m\) негативний, також відбувається вертикальне відображення графіка. Дивлячись на деякі приклади також допоможе показати вплив нахилу на форму графіка:
В\(f(x)=mx+b\),\(b\) діє як вертикальний зсув, переміщаючи графік вгору і вниз, не впливаючи на нахил лінії. Деякі приклади:
Спробуйте самі за допомогою цього аплету:
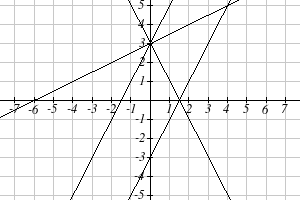
Зіставте кожне рівняння з однією з рядків на графіку нижче\[\begin{align*} f(x) & = 2x+3\\ g(x) & = 2x-3\\ h(x) & = -2x+3\\ j(x) & = \frac{1}{2}x+3 \end{align*}\]
Рішення
Лише один графік має вертикальний перехоплення -3, тому ми можемо негайно зіставити цей графік з\(g(x)\). Для трьох графіків з вертикальним перехопленням на 3, тільки один має негативний нахил, так що ми можемо зіставити цю лінію с\(h(x)\). З двох інших, крутіша лінія буде мати більший нахил, тому ми можемо зіставити цей графік з рівнянням\(f(x)\), а більш плоска лінія з рівнянням\(j(x)\).
Окрім розуміння основної поведінки лінійної функції (збільшення або зменшення, розпізнавання нахилу та вертикального перехоплення), часто корисно знати горизонтальний перехоплення функції - де вона перетинає горизонтальну вісь.
Горизонтальний перехоплення функції - це місце, де графік перетинає горизонтальну вісь. Якщо функція має горизонтальний перехоплення, її завжди можна знайти, вирішивши\(f(x)=0\).
Знайти горизонтальний перехоплення\(f(x)=-3+\frac{1}{2}x\)
Рішення
Встановивши функцію рівну нулю, щоб знайти, який вхід поставить нас на горизонтальну вісь:\[\begin{align*} 0 & = -3+\frac{1}{2}x\\ 3 & = \frac{1}{2}x\\ x & = 6 \end{align*}\] Таким чином, графік перетинає горизонтальну вісь на (6,0).
перетину ліній
Графіки двох ліній будуть перетинатися, якщо вони не паралельні. Вони будуть перетинатися в точці, яка задовольняє обом рівнянням. Щоб знайти цю точку, коли рівняння задаються як функції, ми можемо вирішити для вхідного значення так, що\(f(x)=g(x)\). Іншими словами, ми можемо встановити формули для рядків рівні, і вирішити для вхідних даних, що задовольняє рівнянню.
Економіка говорить нам, що на вільному ринку ціна на товар пов'язана з кількістю, яку будуть поставляти виробники, та кількістю, яку вимагатимуть споживачі. Зростання цін призведе до зниження попиту, тоді як пропозиція має тенденцію до зростання з цінами. Іноді попит і пропозиція моделюються за допомогою лінійних функцій.
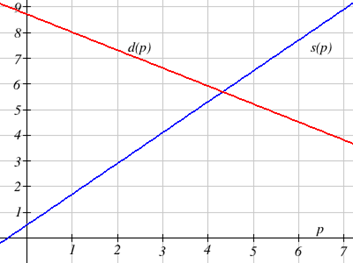
Поставка в тисячах елементів для користувацьких корпусів телефонів може бути змодельована рівнянням,\(s(p)=0.5+1.2p\) тоді як попит може бути змодельований\(d(p)=8.7-0.7p\), де\(p\) в доларах. Знайти рівноважну ціну і кількість, перетин кривих попиту і пропозиції.
Рішення
Налаштування\(s(p)=d(p)\), знаходимо\[\begin{align*} 0.5+1.2p & = 8.7-0.7p\\ 1.9p & = 8.2\\ p & \approx \$4.32 \end{align*}\]
Ми можемо знайти вихідне значення точки перетину, оцінивши будь-яку функцію на цьому вході:\[s(4.32)=0.5+1.2(4.32)\approx 5.68\nonumber \]
Ці лінії перетинаються в точці (4.32, 5.68). Дивлячись на графік, цей результат здається розумним.
Бізнес-додатки
У бізнесі дуже поширеним застосуванням функцій є моделювання витрат, доходів і прибутку.
Коли компанія виробляє\(q\) предмети, загальна вартість - це вартість загальної вартості виробництва цих предметів. Загальна вартість включає як постійні витрати, які є стартовими витратами, такими як обладнання та будівлі, так і змінні витрати, які є витратами, які залежать від кількості вироблених предметів, таких як матеріали та робоча сила.
У найпростішому випадку загальна вартість = (постійні витрати) + (змінні витрати)\(\bf \cdot \)\(\bf q\)
Дохід - це сума грошей, яку компанія приносить від продажів.
У найпростішому випадку Виручка = (Ціна за одиницю товару)\(\bf \cdot \)\(\bf q\)
Прибуток - це сума грошей, яку приносить, після витрат.
Прибуток = Дохід - Витрати
Ми часто говоримо про точку беззбитковості. Це рівень виробництва, де дохід дорівнює собівартості, або еквівалентно, де прибуток дорівнює нулю. Це, як правило, мінімальний рівень продажів, необхідний компанії для отримання прибутку.
Технологічний стартап дивиться на розробку та запуск нового мобільного додатку. Початкова розробка додатка обійдеться в $300 000, а за їхніми оцінками маркетинг і підтримка кожного користувача обійдуться в $0.50. Хоча додаток буде безкоштовним, за їхніми оцінками, вони зможуть принести $2 на користувача в середньому від покупок через додаток. Скільки користувачів компанії потрібно буде беззбитковість?
Рішення
Ми починаємо з моделювання витрат, доходів і прибутку. Нехай\(q\) = кількість користувачів.
Фіксовані (початкові) витрати становлять 300 000 доларів США, а змінні (за одиницю) - 0,50 долара на користувача. Ми можемо записати рівняння загальної вартості:
\(TC(q) = 300,000 + 0.50q\)
Дохід становитиме 2 долари на користувача, тому рівняння доходу буде:
\(R(q) = 2q\)
Ми могли б знайти точку беззбитковості, встановивши загальну вартість, рівну доходу, що еквівалентно знаходженню перетину ліній.
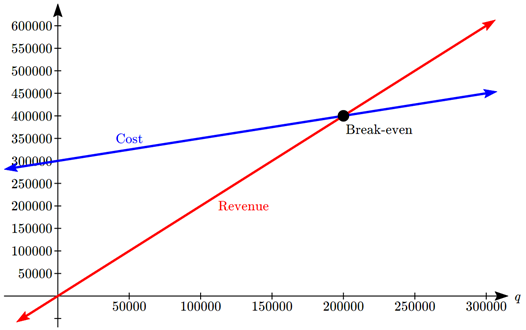
Крім того, ми могли б піти вперед і спочатку знайти рівняння прибутку:
\(P(q) = R(q) - TC(q) = 2q - (300,000+0.50q) = 1.5q - 300,000\)
Точку розриву можна знайти, встановивши прибуток рівний нулю:\[\begin{align*} 0 & = 1.5q - 300,000\\ q & = 200,000 \end{align*}\]
Компанії доведеться придбати 200 000 користувачів, щоб беззбитковість.
В економіці існує модель того, як ціни визначаються на вільному ринку, яка стверджує, що попит і пропозиція на товар пов'язані з ціною. Співвідношення попиту показує кількість певного товару, який споживачі готові придбати за певною ціною. Зазвичай необхідна кількість зменшується для товару, якщо ціна зростає. Співвідношення поставок показує кількість товару, який постачальники готові виробляти за певною ціною продажу. Зазвичай затребувана пропозиція буде збільшуватися, якщо ціна підвищиться. Економічна теорія говорить, що попит і пропозиція будуть взаємодіяти, і перетином буде рівноважна ціна, або ринкова ціна, де кількість, що поставляється і затребувана буде рівною.
\(p\)Якщо ціна товару, то
\(Q_d\)- це кількість, що вимагається
\(Q_s\)- це кількість, що постачається
Крива попиту - це функція зменшення, тоді як крива пропозиції - зростаюча функція.
Перетин кривих - це рівноважна ціна та кількість, яку також називають ринковою ціною та кількістю. Цей пункт часто позначається як\(p^*\),\(Q^*\).
Пізніше в курсі ви вивчите нелінійні криві попиту та пропозиції, але в цьому розділі ми зупинимося на лінійних функціях попиту та пропозиції.
У більшості економічних книг ви побачите криву попиту та пропозиції, записану з ціною як вхідною та кількістю як виходом, наприклад\(Q_d = 140 - 2p\). Однак графіки попиту та пропозиції малюються з ціною на вертикальній осі та кількістю на горизонталі. Ми можемо записати рівняння будь-яким зручним для нас способом.
При ціні $2,50 за галон в певному містечку є попит на 42,5 тисячі галонів газу і запас 20 тисяч галонів. При ціні $3,50 є попит на 25,5 тисячі галонів і пропозиція 28 тисяч галонів. Припускаючи, що попит і пропозиція лінійні, знайдіть рівноважну ціну та кількість.
Рішення
Почнемо з пошуку лінійного рівняння як для попиту, так і для пропозиції. Ми будемо використовувати ціну,\(p\) в доларах, як вихід і кількість,\(q\) в тисячах галонів, як вхід.
Для подачі маємо точки (20, 2,50) і (28, 3,50).
Знаходження ухилу:\(m = \dfrac{3.50-2.50}{28-20} = \frac{1}{8}\)
Ми знаємо, що рівняння буде виглядати так\(p = \frac{1}{8}q+b\), тому підставляючи в (20, 2.50)\[\begin{align*} 2.5 & = \frac{1}{8}(20) +b \\ 2.5 & = 2.5 +b \\ q & = 0 \end{align*}\]
Рівняння подачі таке:\(p = \frac{1}{8}q\)
Для попиту у нас є точки (42,5, 2,50) і (25,5, 3,50). Використовуючи подібний підхід, ми можемо знайти рівняння попиту таке:\(p = -\frac{1}{17}q+5\)
Щоб знайти рівновагу, виставимо пропозицію, рівну попиту:
\(\frac{1}{8}q = -\frac{1}{17}q+5\)
Множивши через 8 (17) = 136, щоб очистити дроби,
\(136\left(\frac{1}{8}q\right) = 136\left(-\frac{1}{17}q+5\right)\)
\(17q = -8q+680\)
Тепер вирішуємо для\(q\)
\(25q = 680\)
\(q = 27.2\)
Щоб знайти рівноважну ціну, ми можемо замінити це значення назад у будь-яке рівняння:
\(p = \frac{1}{8}(27.2) = 3.4\)
Рівноважна кількість складе 27,2 тис. Галонів газу за ціною $3,40.