7.1: Інтеграція частинами
- Page ID
- 62161
- Визнайте, коли використовувати інтеграцію по частинам.
- Використовуйте формулу інтеграції по частинам для вирішення проблем інтеграції.
- Використовуйте формулу інтеграції по частинам для певних інтегралів.
На даний момент ми маємо досить ретельну процедуру того, як оцінити багато основних інтегралів. Однак, хоча ми можемо інтегруватися,\(∫x \sin (x^2)\,dx\) використовуючи підміну\(u=x^2\), щось таке просте, як і нам\(∫x\sin x\,\,dx\) кидає виклик. Багато студентів хочуть знати, чи існує правило продукту для інтеграції. Немає, але існує методика, заснована на правилі продукту для диференціації, яка дозволяє нам обмінювати один інтеграл на інший. Ми називаємо цю техніку інтеграцією частинами.
Формула інтеграції по частинам
Якщо\(h(x)=f(x)g(x)\), то скориставшись правилом продукту, отримуємо
\[h′(x)=f′(x)g(x)+g′(x)f(x). \label{eq1} \]
Хоча спочатку це може здатися контрпродуктивним, давайте тепер інтегруємо обидві сторони Equation\ ref {eq1}:
\[∫h′(x)\,\,dx=∫(g(x)f′(x)+f(x)g′(x))\,\,dx. \nonumber \]
Це дає нам
\[ h(x)=f(x)g(x)=∫g(x)f′(x)\,dx+∫f(x)g′(x)\,\,dx. \nonumber \]
Тепер вирішуємо для\(∫f(x)g′(x)\,\,dx:\)
\[ ∫f(x)g′(x)\,dx=f(x)g(x)−∫g(x)f′(x)\,\,dx. \nonumber \]
Здійснюючи заміни\(u=f(x)\) і\(v=g(x)\), які в свою чергу роблять\(du=f′(x)\,dx\) і\(dv=g′(x)\,dx\), ми маємо більш компактну форму
\[ ∫u\,dv=uv−∫v\,du. \nonumber \]
\(v=g(x)\)Дозволяти\(u=f(x)\) і бути функції з неперервними похідними. Тоді формула інтеграції за частинами для інтеграла, що включає ці дві функції, така:
\[∫u\,dv=uv−∫v\,du. \label{IBP} \]
Перевага використання формули інтеграції по частинам полягає в тому, що ми можемо використовувати її для обміну одного інтеграла на інший, можливо, простіше, інтеграл. Наступний приклад ілюструє його використання.
Використання інтеграції по частинам з\(u=x\) і\(dv=\sin x\,\,dx\) для оцінки
\[∫x\sin x\,\,dx. \nonumber \]
Рішення
Вибираючи\(u=x\), ми маємо\(du=1\,\,dx\). З тих пір\(dv=\sin x\,\,dx\), ми отримуємо
\[v=∫\sin x\,\,dx=−\cos x. \nonumber \]
Зручно відстежувати ці значення наступним чином:
- \(u=x\)
- \(dv=\sin x\,\,dx\)
- \(du=1\,dx\)
- \(v=∫\sin x\,\,dx=−\cos x.\)
Застосування формули інтеграції по частинам (Equation\ ref {IBP}) призводить до
\[ \begin{align} ∫x\sin x\,\,dx &=(x)(−\cos x)−∫(−\cos x)(1\,\,dx) \tag{Substitute} \\[4pt] &=−x\cos x+∫\cos x\,\,dx \tag{Simplify} \end{align} \]
Тоді використовуйте
\[∫\cos x\,\,dx =\sin x+C. \nonumber \]
для отримання
\[∫x\sin x\,\,dx =−x\cos x+\sin x+C. \nonumber \]
Аналіз
На даний момент, ймовірно, є кілька пунктів, які потребують роз'яснення. Перш за все, вам може бути цікаво, що б сталося, якби ми вибрали\(u=\sin x\) і\(dv=x\). Якби ми це зробили, то мали б\(du=\cos x\) і\(v=\dfrac{1}{2}x^2\). Таким чином, після застосування інтеграції частинами (Equation\ ref {IBP}), ми маємо
\[ ∫x\sin x\,\,dx=\dfrac{1}{2}x^2\sin x−∫\dfrac{1}{2}x^2\cos x\,\,dx. \nonumber \]
На жаль, з новим інтегралом ми знаходимося в не кращому становищі, ніж раніше. Важливо пам'ятати, що коли ми застосовуємо інтеграцію по частинам, нам може знадобитися спробувати кілька варіантів\(u\) і\(dv\) перш ніж знайти вибір, який працює.
По-друге, ви можете задатися питанням, чому, коли ми знаходимо\(v=∫\sin x\,\,dx=−\cos x\), ми не використовуємо\(v=−\cos x+K.\) Щоб побачити, що це не має значення, ми можемо переробити проблему, використовуючи\(v=−\cos x+K\):
\[ \begin{align*} ∫x\sin x\,\,dx &=(x)(−\cos x+K)−∫(−\cos x+K)(1\,\,dx) \\[4pt] &=−x\cos x+Kx+∫\cos x\,\,dx−∫K\,\,dx \\[4pt] &=−x\cos x+Kx+\sin x−Kx+C \\[4pt] &=−x\cos x+\sin x+C. \end{align*}\]
Як бачите, це не має різниці в кінцевому рішенні.
Нарешті, ми можемо перевірити, щоб переконатися, що наше антипохідне правильне, диференціюючи\(−x\cos x+\sin x+C:\)
\[ \begin{align*} \dfrac{d}{\,dx}(−x\cos x+\sin x+C) = \cancel{(−1)\cos x} + (−x)(−\sin x) + \cancel{\cos x} \\[4pt] =x\sin x \end{align*}\]
Тому антидериватив перевіряється.
Оцініть\(∫xe^{2x}\,dx\) за допомогою формули інтеграції по частинам (Equation\ ref {IBP}) з\(u=x\) і\(dv=e^{2x}\,\,dx\).
- Підказка
-
Знайдіть\(du\) і\(v\), і використовуйте попередній приклад як орієнтир.
- Відповідь
-
\[ ∫xe^{2x}\,\,dx=\dfrac{1}{2}xe^{2x}−\dfrac{1}{4}e^{2x}+C \nonumber \]
Природне питання, яке потрібно задати на цьому етапі, полягає в тому, як ми знаємо, як вибрати\(u\) і\(dv\)? Іноді це питання проб і помилок; однак абревіатура LIATE часто може допомогти взяти деякі здогадки з нашого вибору. Цей акронім розшифровується як L огарифмічні функції, I обернені тригонометричні функції, A алгебраїчні функції, T ригонометричні функції, і E експоненціальні функції. Ця мнемоніка служить допоміжним засобом у визначенні відповідного вибору для\(u\). Тип функції в інтегралі, який з'являється першим у списку, повинен бути нашим першим вибором\(u\).
Наприклад, якщо інтеграл містить логарифмічну функцію та алгебраїчну функцію, ми повинні\(u\) вибрати логарифмічну функцію, оскільки L стоїть перед A в LIATE. Інтеграл у прикладі\(\PageIndex{1}\) має тригонометричну функцію (\(\sin x\)) та алгебраїчну функцію (\(x\)). Оскільки A приходить до T в LIATE, ми\(u\) вирішили бути алгебраїчною функцією. Коли ми вибрали\(u\),\(dv\) вибирається решта функції, яку потрібно інтегрувати, разом з\(\,dx\).
Чому працює ця мнемоніка? Пам'ятайте, що все, що ми обираємо,\(dv\) має бути чимось, що ми можемо інтегрувати. Оскільки у нас немає інтеграційних формул, які дозволяють інтегрувати прості логарифмічні функції та обернені тригонометричні функції, має сенс, що їх не слід вибирати як значення для\(dv\). Отже, вони повинні бути на чолі списку як вибір для\(u\). Таким чином, ми ставимо LI на початку мнемоніки. (Ми могли б так само легко почати з IL, оскільки ці два типи функцій не з'являться разом у проблемі інтеграції за частинами.) Експоненціальні та тригонометричні функції знаходяться в кінці нашого списку, оскільки їх досить легко інтегрувати та робити хороший вибір\(dv\). Таким чином, ми маємо TE в кінці нашої мнемоніки. (Ми могли б так само легко використовувати ET в кінці, оскільки, коли ці типи функцій з'являються разом, це зазвичай насправді не має значення, який з них є\(u\) і який\(dv\).) Алгебраїчні функції, як правило, легко інтегрувати і диференціювати, і вони знаходяться в середині мнемоніки.
Оцінити\[∫\dfrac{\ln x}{x^3}\,\,dx. \nonumber \]
Рішення
Почніть з переписування інтеграла:
\[∫\dfrac{\ln x}{x^3}\,\,dx=∫x^{−3}\ln x\,\,dx. \nonumber \]
Оскільки цей інтеграл містить алгебраїчну функцію\(x^{−3}\) і логарифмічну функцію\(\ln x\), вибирайте\(u=\ln x\), оскільки\(L\) настає перед A в LIATE. Після того, як ми вибрали\(u=\ln x\), ми повинні вибрати\(dv=x^{−3}\,dx\).
Далі, оскільки\(u=\ln x,\) ми\(du=\dfrac{1}{x}\,dx.\) також,\(v=∫x^{−3}\,dx=−\dfrac{1}{2}x^{−2}.\) підсумовуючи,
- \(u=\ln x\)
- \(du=\dfrac{1}{x}\,dx\)
- \(dv=x^{−3}\,dx\)
- \(v=∫x^{−3}\,dx=−\dfrac{1}{2}x^{−2}.\)
Підстановка в формулу інтеграції по частинам (Equation\ ref {IBP}) дає
\[ \begin{align*} ∫\dfrac{\ln x}{x^3}\,dx &=∫x^{−3}\ln x\,dx=(\ln x)(−\dfrac{1}{2}x^{−2})−∫(−\dfrac{1}{2}x^{−2})(\dfrac{1}{x}\,dx) \\[4pt] &=−\dfrac{1}{2}x^{−2}\ln x+∫\dfrac{1}{2}x^{−3}\,\,dx \\[4pt] &=−\dfrac{1}{2}x^{−2}\ln x−\dfrac{1}{4}x^{−2}+C\ \\[4pt] &=−\dfrac{1}{2x^2}\ln x−\dfrac{1}{4x^2}+C \end{align*} \nonumber \]
Оцінити\[∫x\ln x \,\,dx. \nonumber \]
- Підказка
-
Використовувати\(u=\ln x\) і\(dv=x\,\,dx\).
- Відповідь
-
\[∫x\ln x \,\,dx=\dfrac{1}{2}x^2\ln x−\dfrac{1}{4}x^2+C \nonumber \]
У деяких випадках, як і в наступних двох прикладах, може знадобитися застосовувати інтеграцію частинами не один раз.
Оцінити\[∫x^2e^{3x}\,dx. \nonumber \]
Рішення
Використовуючи LIATE, вибираємо\(u=x^2\) і\(dv=e^{3x}\,dx\). Таким чином,\(du=2x\,dx\) і\(v=∫e^{3x}\,dx=\left(\dfrac{1}{3}\right)e^{3x}\). Тому,
- \(u=x^2\)
- \(du=2x\,dx\)
- \(dv=e^{3x}\,dx\)
- \(v=∫e^{3x}\,dx=\dfrac{1}{3}e^{3x}.\)
Підстановка в рівняння\ ref {IBP} виробляє
\[∫x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−∫\dfrac{2}{3}xe^{3x}\,dx. \label{3A.2} \]
Ми все ще не можемо інтегруватися\(∫\dfrac{2}{3}xe^{3x}\,dx\) безпосередньо, але інтеграл тепер має меншу потужність\(x\). Ми можемо оцінити цей новий інтеграл, використовуючи інтеграцію частинами знову. Для цього вибираємо
\[u=x \nonumber \]
і
\[dv=\dfrac{2}{3}e^{3x}\,dx. \nonumber \]
Таким чином,
\[du=\,dx \nonumber \]
і
\[v=∫\left(\dfrac{2}{3}\right)e^{3x}\,dx=\left(\dfrac{2}{9}\right)e^{3x}. \nonumber \]
Тепер у нас є
- \(u=x\)
- \(du=\,dx\)
- \(dv=\dfrac{2}{3}e^{3x}\,dx\)
- \(\displaystyle v=∫\dfrac{2}{3}e^{3x}\,dx=\dfrac{2}{9}e^{3x}.\)
Підстановка назад в рівняння\ ref {3A.2} дає
\[∫x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−\left(\dfrac{2}{9}xe^{3x}−∫\dfrac{2}{9}e^{3x}\,dx\right). \nonumber \]
Оцінивши останній інтеграл і спростивши, отримаємо
\[∫x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−\dfrac{2}{9}xe^{3x}+\dfrac{2}{27}e^{3x}+C. \nonumber \]
Оцінити
\[∫t^3e^{t^2}dt. \nonumber \]
Рішення
Якщо ми використовуємо суворе тлумачення мнемонічного LIATE, щоб зробити свій вибір\(u\), ми закінчуємо\(u=t^3\) і\(dv=e^{t^2}dt\). На жаль, цей вибір не спрацює, тому що ми не можемо оцінити\(∫e^{t^2}dt\). Однак, оскільки ми можемо оцінити\(∫te^{t^2}\,dx\), ми можемо спробувати вибрати\(u=t^2\) і\(dv=te^{t^2}dt.\) З цим вибором у нас є
- \(u=t^2\)
- \(du=2tdt\)
- \(dv=te^{t^2}dt\)
- \(v=∫te^{t^2}dt=\dfrac{1}{2}e^{t^2}.\)
Таким чином, отримуємо
\[\begin{align*} ∫t^3e^{t^2}dt =\dfrac{1}{2}t^2e^{t^2}−∫\dfrac{1}{2}e^{t^2}2t\,dt \\[4pt] =\dfrac{1}{2}t^2e^{t^2}−\dfrac{1}{2}e^{t^2}+C. \end{align*}\]
Оцінити\[∫\sin (\ln x)\,dx. \nonumber \]
Рішення
Цей інтеграл, здається, має лише одну функцію, а саме,\(\sin (\ln x)\) —однак, ми завжди можемо використовувати постійну функцію 1 як іншу функцію. У цьому прикладі давайте виберемо\(u=\sin (\ln x)\) і\(dv=1\,dx\). (Рішення використовувати\(u=\sin (\ln x)\) просте. Ми не можемо вибрати,\(dv=\sin (\ln x)\,dx\) тому що якби ми могли інтегрувати його, ми б не використовували інтеграцію частинами в першу чергу!) Отже,\(du=(1/x)\cos (\ln x) \,dx\) і\(v=∫ 1 \,dx=x.\) після застосування інтеграції частинами до інтегралу і спрощення, ми маємо
\[∫\sin \left(\ln x\right) \,dx=x \sin (\ln x)−\int \cos (\ln x)\,dx. \nonumber \]
На жаль, цей процес залишає нам новий інтеграл, який дуже схожий на оригінал. Однак давайте подивимося, що станеться, коли ми знову застосуємо інтеграцію частинами. Цього разу давайте виберемо\(u=\cos (\ln x)\) і\(dv=1\,dx,\) зробимо\(du=−(1/x)\sin (\ln x)\,dx\) і\(v=∫1\,dx=x.\)
Підставляючи, ми маємо
\[∫\sin (\ln x)\,dx=x \sin (\ln x)−(x \cos (\ln x)-∫−\sin (\ln x)\,dx). \nonumber \]
Після спрощення отримуємо
\[∫\sin (\ln x)\,dx=x\sin (\ln x)−x \cos (\ln x)−∫\sin (\ln x)\,dx. \nonumber \]
Останній інтеграл тепер такий же, як і оригінал. Може здатися, що ми просто пішли по колу, але тепер ми можемо реально оцінити інтеграл. Щоб побачити, як це зробити чіткіше, підставляйте\(I=∫\sin (\ln x)\,dx.\) Таким чином, рівняння стає
\[I=x \sin (\ln x)−x \cos (\ln x)−I. \nonumber \]
Спочатку додайте\(I\) до обох сторін рівняння, щоб отримати
\[2I=x \sin (\ln x)−x \cos (\ln x). \nonumber \]
Далі ділимо на 2:
\[I=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x). \nonumber \]
Підставляючи\(I=∫\sin (\ln x)\,dx\) знову, ми маємо
\[ \int \sin (\ln x) \,dx=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x). \nonumber \]
З цього ми бачимо, що\((1/2)x \sin (\ln x)−(1/2)x \cos (\ln x)\) є антипохідним від\(\sin (\ln x)\,dx\). Для найбільш загального антидериватива додайте\(+C\):
\[ ∫ \sin (\ln x) \,dx=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x)+C. \nonumber \]
Аналіз
Якщо спочатку цей метод здається трохи дивним, ми можемо перевірити відповідь шляхом диференціації:
\[\begin{align*} \dfrac{d}{\,dx}\left(\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x\cos (\ln x)\right) \\[4pt] &=\dfrac{1}{2}(\sin (\ln x))+\cos (\ln x)⋅\dfrac{1}{x}⋅\dfrac{1}{2}x−\left(\dfrac{1}{2}\cos (\ln x)−\sin (\ln x)⋅\dfrac{1}{x}⋅\dfrac{1}{2}x\right) \\[4pt] &=\sin (\ln x). \end{align*}\]
Оцінити\[∫x^2\sin x\,dx. \nonumber \]
- Підказка
-
Це схоже на Приклади\(\PageIndex{3A}\) -\(\PageIndex{3C}\).
- Відповідь
-
\[∫x^2\sin x\,dx=−x^2\cos x+2x\sin x+2\cos x+C \nonumber \]
Інтеграція частинами для визначених інтегралів
Тепер, коли ми успішно використали інтеграцію частинами для оцінки невизначеного інтегралу, звернемо увагу на певні інтеграли. Техніка інтеграції дійсно однакова, тільки ми додаємо крок для оцінки інтеграла на верхній і нижній межі інтеграції.
\(v=g(x)\)Дозволяти\(u=f(x)\) і бути функції з неперервними похідними на [\(a,b\)]. Тоді
\[∫^b_a u\,dv=uv\Big|^b_a−∫^b_a v\, du \nonumber \]
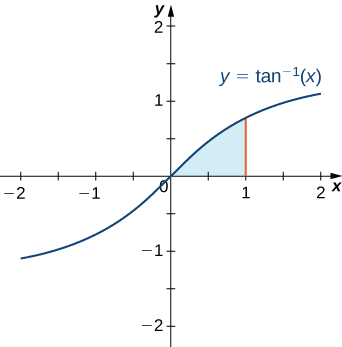
Знайти площу області, обмеженої вище графіком\(y=\tan^{−1}x\) і нижче по\(x\) осі -над інтервалом [\(0,1\)].
Рішення
Ця область показана на малюнку\(\PageIndex{1}\). Щоб знайти площу, ми повинні оцінити
\[∫^1_0 \tan^{−1}x\, \,dx. \nonumber \]
Для цього невід'ємного, давайте виберемо\(u=tan^{−1}x\) і\(dv=\,dx\), тим самим зробивши\(du=\dfrac{1}{x^2+1}\,dx\) і\(v=x\). Після застосування формули інтеграції по частинам (Equation\ ref {IBP}) отримуємо
\[ \text{Area}=\left. x \tan^{−1} x \right|^1_0−∫^1_0 \dfrac{x}{x^2+1} \,dx. \nonumber \]
Використовуйте\(u\) -підстановку для отримання
\[∫^1_0\dfrac{x}{x^2+1}\,dx=\left.\dfrac{1}{2}\ln \left(x^2+1\right) \right|^1_0. \nonumber \]
Таким чином,
\[\text{Area}=x \tan^{−1}x \Big|^1_0− \left.\dfrac{1}{2}\ln \left( x^2+1 \right) \right|^1_0=\left(\dfrac{π}{4}−\dfrac{1}{2}\ln 2\right) \,\text{units}^2. \nonumber \]
На даний момент це може бути не поганою ідеєю зробити «перевірку реальності» на розумність нашого рішення. Оскільки\(\dfrac{π}{4}−\dfrac{1}{2}\ln 2≈0.4388\,\text{units}^2,\) і від малюнка\(\PageIndex{1}\) ми очікуємо, що наша область буде трохи меншою, ніж\(0.5\,\text{units}^2,\) це рішення здається розумним.
Знайдіть об'єм твердого тіла, отриманого обертанням області, обмеженої\(f(x)=e^{−x},\) графіком\(x\) -осі,\(y\) -осі та лінією\(x=1\) навколо\(y\) -осі.
Рішення
Оптимальним варіантом вирішення цієї проблеми є використання методу оболонки. Почніть з ескізу області, яку потрібно обертати, разом із типовим прямокутником (рис.\(\PageIndex{2}\)).
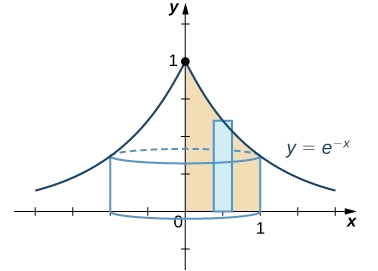
Щоб знайти обсяг за допомогою оболонок, ми повинні оцінити
\[2π∫^1_0xe^{−x}\,dx. \label{4B.1} \]
Для цього нехай\(u=x\) і\(dv=e^{−x}\). Ці варіанти призводять до\(du=\,dx\) і\(v=∫e^{−x}\,dx=−e^{−x}.\) Використовуючи формулу Shell Method, ми отримуємо
\ [\ почати {вирівнювати*}\ текст {Том} &=2π^1_0xe^ {−x}\, dx\\ [4pt] = 2π\ ліворуч (−xe^ {−x}\ big|^1_0+^1_0e^ {−x}\, dx\ праворуч)\ tag {Використовуйте інтеграцію частинами}\\ [4pt]
&π ліворуч (-e^ {-1} + 0 - e^ {-x}\ Великий|^1_0\ праворуч)\\ [4pt]
&= 2π\ ліворуч (-e^ {-1} - e^ {-1} + 1\ праворуч)\\ [4pt]
&= 2π\ ліворуч (1 -\ dfrac {2} {e}\ праворуч)\,\ текст {одиниці} ^3. \ tag {Оцінити і спростити}\ end {align*}\]
Аналіз
Знову ж таки, це гарна ідея, щоб перевірити розумність нашого рішення. Ми спостерігаємо, що тверде тіло має об'єм трохи менше, ніж циліндр радіуса\(1\) і висоти\(1/e\) додається до обсягу конуса базового радіуса\(1\) і висоти\(1−\dfrac{1}{e}.\) Отже, тверде тіло повинно мати об'єм трохи менше
\[π(1)^2\dfrac{1}{e}+\left(\dfrac{π}{3}\right)(1)^2\left(1−\dfrac{1}{e}\right)=\dfrac{2π}{3e}+\dfrac{π}{3}≈1.8177\,\text{units}^3. \nonumber \]
Так як\(2π−\dfrac{4π}{e}≈1.6603,\) ми бачимо, що наш розрахунковий обсяг є розумним.
Оцінити\[∫^{π/2}_0x\cos x\,dx. \nonumber \]
- Підказка
-
Використовувати рівняння\ ref {IBP} з\(u=x\) і\(dv=\cos x\,dx.\)
- Відповідь
-
\[∫^{π/2}_0x\cos x\,dx = \dfrac{π}{2}−1 \nonumber \]
Ключові поняття
- Формула інтеграції по частинам (Equation\ ref {IBP}) дозволяє обмінюватися одним інтегралом на інший, можливо, більш легким, інтегралом.
- Інтеграція частинами застосовується як до визначених, так і до невизначеного інтегралів.
Ключові рівняння
- Інтеграція за формулою частин
\(\displaystyle ∫u\,dv=uv−∫v\,du\)
- Інтеграція частинами для певних інтегралів
\(\displaystyle ∫^b_au\,dv=uv\Big|^b_a−∫^b_av\,du\)
Глосарій
- інтеграція частинами
- методика інтеграції, що дозволяє обмінюватися одним інтегралом на інший за допомогою формули\(\displaystyle ∫u\,dv=uv−∫v\,du\)
