7.3: Тригонометрична заміна
- Page ID
- 62118
- Вирішити інтеграційні задачі за участю квадратного кореня суми або різниці двох квадратів.
У цьому розділі ми досліджуємо інтеграли, що містять вирази\(\sqrt{a^2+x^2}\) виду\(\sqrt{a^2−x^2}\), і\(\sqrt{x^2−a^2}\), де значення\(a\) є додатними. Ми вже стикалися і оцінювали інтеграли, що містять деякі вирази цього типу, але багато хто все ще залишаються недоступними. Техніка тригонометричного заміщення дуже стане в нагоді при оцінці цих інтегралів. Цей метод використовує підстановку для перезапису цих інтегралів як тригонометричних інтегралів.
Інтеграли за участю\(\sqrt{a^2−x^2}\)
Перш ніж розробляти загальну стратегію для інтегралів\(\sqrt{a^2−x^2}\), що містять, розглянемо інтеграл\(\displaystyle ∫\textstyle\sqrt{9−x^2}dx.\) Цей інтеграл не може бути оцінений за допомогою жодної з методів, про які ми обговорювали досі. Однак, якщо ми робимо підстановку\(x=3\sin θ\), ми маємо\(dx=3\cos θ \, dθ.\) Після підстановки в інтеграл, ми маємо
\[ ∫\sqrt{9−x^2}\,dx=∫\textstyle\sqrt{ 9−(3\sin θ)^2}\cdot 3\cos θ \,dθ. \nonumber \]
Після спрощення ми маємо
\[ ∫\sqrt{ 9−x^2}\,dx=∫ 9\textstyle\sqrt{1−\sin^2θ}\cdot\cos θ \, dθ. \nonumber \]
\(1−\sin^2θ=\cos^2θ,\)Дозволивши нам тепер
\[ ∫\sqrt{ 9−x^2}\,dx=∫ 9\textstyle\sqrt{\cos^2θ}\cos θ \, dθ. \nonumber \]
Якщо припустити\(\cos θ≥0\), що ми маємо
\[ ∫\textstyle\sqrt{ 9−x^2}\,dx=∫ 9\cos^2θ \, dθ. \nonumber \]
На цьому етапі ми можемо оцінити інтеграл, використовуючи методи, розроблені для інтеграції повноважень і добутків тригонометричних функцій. Перш ніж завершити цей приклад, давайте поглянемо на загальну теорію, що стоїть за цією ідеєю.
Для оцінки інтегралів за\(\sqrt{a^2−x^2}\) участю виробляємо підстановку\(x=a\sin θ\) і\(dx=a\cos θ\). Щоб побачити, що це насправді має сенс, розглянемо наступний аргумент: Домен\(\sqrt{a^2−x^2}\) is\([−a,a]\). Таким чином,
\[−a≤x≤a. \nonumber \]
Отже,
\[−1≤\dfrac{x}{a}≤1. \nonumber \]
Оскільки діапазон\(\sin x\) над\([−(π/2),π/2]\) є\([−1,1]\), існує унікальний кут, що\(θ\) задовольняє\(−(π/2)≤θ≤π/2\) так\(\sin θ=x/a\), що, або еквівалентно, так що\(x=a\sin θ\). Якщо ми підставимо\(x=a\sin θ\) в\(\sqrt{a^2−x^2}\), ми отримаємо
\ [\ почати {align*}\ sqrt {a^2−x^2} &=\ sqrt {a^2− (a\ sin θ) ^2} &\ текст {Нехай} x = a\ sin θ\ текст {де} -\ dfrac {π} {2} ≤θ ≤\ dfrac {π} {2}.\\ [4pt]
&\ текст {Спрощення.}\\ [4pt]
&=\ sqrt {a^2−a^2\ sin^2θ} &\ текст {Фактор з} a^2.\\ [4pt]
&=\ sqrt {a^2 (1−\ sin^2θ)} &\ текст {Заміна} 1−\ sin^2x=\ cos^2x.\\ [4pt]
&=\ sqrt {a^2\ cos^2θ} &\ text {Візьміть квадратний корінь.}\\ [4pt]
&=|a\ cos θ |\\ [
4pt]\ end {вирівнювати*}\]
Так як\(\cos x≥0\) на\(−\dfrac{π}{2}≤θ≤\dfrac{π}{2}\) і\(a>0, |a\cos θ|=a\cos θ.\) Ми бачимо, з цієї дискусії, що шляхом підстановки\(x=a\sin θ\), ми можемо перетворити інтеграл за участю радикала в інтеграл за участю тригонометричних функцій. Після того, як ми оцінюємо інтеграл, ми можемо перетворити рішення назад у вираз за участю\(x\). Щоб побачити, як це зробити, давайте почнемо з припущення, що\(0<x<a\). В даному випадку,\(0<θ<\dfrac{π}{2}\). Оскільки\(\sin θ=\dfrac{x}{a}\), ми можемо намалювати опорний трикутник на малюнку,\(\PageIndex{1}\) щоб допомогти у вираженні значень тригонометричних функцій\(\cos θ, \, \tan θ,\) та решти тригонометричних функцій через x. Можна показати, що цей трикутник фактично створює правильні значення тригонометричних функцій, що оцінюються на\(θ\) для всіх\(θ\) ситних\(−\dfrac{π}{2}≤θ≤\dfrac{π}{2}\). Корисно спостерігати, що вираз\(\sqrt{a^2−x^2}\) насправді з'являється як довжина однієї сторони трикутника. Останній, повинен\(θ\) з'явитися сам по собі, використовуємо\(θ=\sin^{−1}\left(\dfrac{x}{a}\right).\)
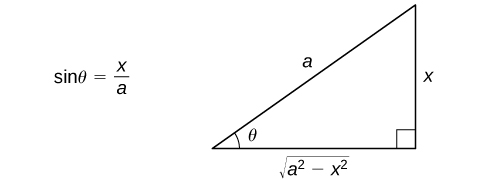
Істотна частина цієї дискусії узагальнена в наступній стратегії вирішення проблем.
- Це гарна ідея, щоб переконатися, що інтеграл не може бути оцінений легко по-іншому. Наприклад, хоча цей метод може бути застосований до інтегралів виду\(\displaystyle ∫\dfrac{1}{\sqrt{a^2−x^2}}dx\),\(\displaystyle ∫\dfrac{x}{\sqrt{a^2−x^2}}dx,\) і кожен з\(\displaystyle ∫x\sqrt{a^2−x^2}\,dx,\) них може бути інтегрований безпосередньо або за формулою, або простим\(u\) -підстановкою.
- Зробіть заміну\(x=a \sin θ\) і\(dx=a\cos θ \,dθ.\) зверніть увагу: Ця заміна дає\(\sqrt{a^2−x^2}=a\cos θ.\)
- Спростити вираз.
- Оцініть інтеграл за допомогою прийомів з розділу про тригонометричні інтеграли.
- Використовуйте опорний трикутник з рисунка 1, щоб переписати результат через\(x\). Можливо, вам також доведеться використовувати деякі тригонометричні ідентичності та відносини.\(θ=\sin^{−1}\left(\dfrac{x}{a}\right).\)
Наступний приклад демонструє застосування цієї стратегії вирішення проблем.
Оцінити
\[ ∫\sqrt{ 9−x^2}dx. \nonumber \]
Рішення
Почніть з підстановки\(x=3\sin θ\) і\(dx=3\cos θ \, dθ.\) Оскільки\(\sin θ=\dfrac{x}{3}\), ми можемо побудувати опорний трикутник, показаний на малюнку 2.
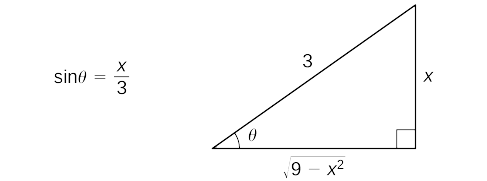
Таким чином,
\[ ∫\sqrt{9−x^2}\,dx=∫\sqrt{ 9−(3\sin θ)^2}3\cos θ\,dθ \nonumber \]
Замінник\(x=3\sin θ\) і\(dx=3\cos θ \,dθ\).
\(=∫\sqrt{ 9(1−\sin^2θ)}\cdot 3\cos θ \, dθ\)Спростити.
\(=∫\sqrt{ 9\cos^2θ}\cdot 3\cos θ \, dθ\)Замінник\(\cos^2θ=1−\sin^2θ\).
\(=∫ 3|\cos θ|3\cos θ \, dθ\)Візьміть квадратний корінь.
\(=∫ 9\cos^2θ \, dθ\)Спростити. Так як\(−\dfrac{π}{2}≤θ≤\dfrac{π}{2},\cos θ≥0\) і\(|\cos θ|=\cos θ.\)
\(=∫ 9\left(\dfrac{1}{2}+\dfrac{1}{2}\cos(2θ)\right)\,dθ\)Використовуйте стратегію інтеграції рівної сили\(\cos θ\).
\(=\dfrac{9}{2}θ+\dfrac{9}{4}\sin(2θ)+C\)Оцініть інтеграл.
\(=\dfrac{9}{2}θ+\dfrac{9}{4}(2\sin θ\cos θ)+C\)
Замінник\(\sin(2θ)=2\sin θ\cos θ\).
\(=\dfrac{9}{2}\sin^{−1}\left(\dfrac{x}{3}\right)+\dfrac{9}{2}⋅\dfrac{x}{3}⋅\dfrac{\sqrt{9−x^2}}{3}+C\)Замінник\(\sin^{−1}\left(\dfrac{x}{3}\right)=θ\) і\(\sin θ=\frac{x}{3}\). Скористайтеся еталонним трикутником, щоб побачити це\(\cos θ=\dfrac{\sqrt{9−x^2}}{3} \) і зробити цю заміну. Спростити.
\(=\dfrac{9}{2}\sin^{−1}\left(\dfrac{x}{3}\right)+\dfrac{x\sqrt{9−x^2}}{2}+C.\)Спростити.
Оцінити
\[ ∫\dfrac{\sqrt{4−x^2}}{x}dx. \nonumber \]
Рішення
Спочатку зробіть заміни\(x=2\sin θ\) і\(dx=2\cos θ\,dθ\). Так як\(\sin θ=\dfrac{x}{2}\), ми можемо побудувати опорний трикутник, показаний на малюнку\(\PageIndex{3}\).
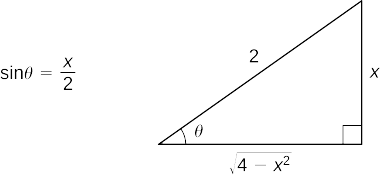
Таким чином,
\(∫\dfrac{\sqrt{4−x^2}}{x}dx=∫\dfrac{\sqrt{4−(2\sin θ)^2}}{2\sin θ}2\cos θ \, dθ\)Замінник\(x=2\sin θ\) і\(dx=2\cos θ\,dθ.\)
\(=∫\dfrac{2\cos^2θ}{\sin θ}\,dθ\)Підставляємо\(\cos^2θ=1−\sin^2θ\) і спрощуємо.
\(=∫\dfrac{2(1−\sin^2θ)}{\sin θ}\,dθ\)Замінник\(\cos^2θ=1−\sin^2θ\).
\(=∫ (2\csc θ−2\sin θ)\,dθ\)Відокремте чисельник, спростіть і використовуйте\(\csc θ=\dfrac{1}{\sin θ}\).
\(=2 \ln |\csc θ−\cot θ|+2\cos θ+C\)Оцініть інтеграл.
\(=2 \ln \left|\dfrac{2}{x}−\dfrac{\sqrt{4−x^2}}{x}\right|+\sqrt{4−x^2}+C.\)Використовуйте опорний трикутник, щоб переписати вираз з точки зору\(x\) і спростити.
У наступному прикладі ми бачимо, що у нас іноді є вибір методів.
Оцініть\(∫ x^3\sqrt{1−x^2}dx\) два способи: спочатку за допомогою підстановки,\(u=1−x^2\) а потім за допомогою тригонометричної підстановки.
Спосіб 1
Нехай\(u=1−x^2\) і звідси\(x^2=1−u\). Таким чином,\(du=−2x\,dx.\) в цьому випадку інтеграл стає
\(∫ x^3\sqrt{1−x^2}\,dx=−\dfrac{1}{2}∫ x^2\sqrt{1−x^2}(−2x\,dx)\)Зробіть заміну.
\(=−\dfrac{1}{2}∫ (1−u)\sqrt{u}\,du\)Розгорніть вираз.
\(=−\dfrac{1}{2}∫(u^{1/2}−u^{3/2})\,du\)Оцініть інтеграл.
\(=−\dfrac{1}{2}(\dfrac{2}{3}u^{3/2}−\dfrac{2}{5}u^{5/2})+C\)Перепишіть в терміні x.
\(=−\dfrac{1}{3}(1−x^2)^{3/2}+\dfrac{1}{5}(1−x^2)^{5/2}+C.\)
Спосіб 2
Нехай\(x=\sin θ\). У цьому випадку,\(dx=\cos θ \, dθ.\) Використовуючи цю заміну, ми маємо
\(∫ x^3\sqrt{1−x^2}dx=∫ \sin^3θ\cos^2θ \, dθ\)
\(=∫ (1−\cos^2θ)\cos^2θ\sin θ \, dθ\)Нехай\(u=\cos θ\). Таким чином,\(du=−\sin θ \, dθ.\)
\(=∫ (u^4−u^2)\,du\)
\(=\dfrac{1}{5}u^5−\dfrac{1}{3}u^3+C\)Замінник\(\cos θ=u.\)
\(=\dfrac{1}{5}\cos^5θ−\dfrac{1}{3}\cos^3θ+C\)Використовуйте опорний трикутник, щоб побачити, що\(\cos θ=\sqrt{1−x^2}.\)
\(=\dfrac{1}{5}(1−x^2)^{5/2}−\dfrac{1}{3}(1−x^2)^{3/2}+C.\)
Перепишіть інтеграл,\(\displaystyle ∫\dfrac{x^3}{\sqrt{25−x^2}}\,dx\) використовуючи відповідну тригонометричну підстановку (не оцінюйте інтеграл).
- Підказка
-
Замінник\(x=5\sin θ\) і\(dx=5\cos θ \, dθ.\)
- Відповідь
-
\(\displaystyle ∫ 125\sin^3θ \, dθ\)
Інтеграція виразів за участю\(\sqrt{a^2+x^2}\)
Для інтегралів\(\sqrt{a^2+x^2}\), що містять, давайте спочатку розглянемо область цього виразу. Оскільки\(\sqrt{a^2+x^2}\) визначається для всіх дійсних значень\(x\), ми обмежуємо свій вибір тими тригонометричними функціями, які мають діапазон всіх дійсних чисел. Таким чином, наш вибір обмежується вибором або\(x=a\tan θ\) або\(x=a\cot θ\). Будь-яка з цих замін дійсно працювала б, але стандартна заміна є\(x=a\tan θ\) або, еквівалентно,\(\tan θ=x/a\). При цій заміні ми робимо припущення\(−(π/2)<θ<π/2\), що, так що\(θ=\tan^{−1}(x/a).\) у нас також є Процедура використання цієї заміни викладена в наступній стратегії вирішення проблем.
- Перевірте, чи можна легко оцінити інтеграл за допомогою іншого методу. У деяких випадках зручніше використовувати альтернативний метод.
- Замінник\(x=a\tan θ\) і\(dx=a\sec^2θ \, dθ.\) Це заміщення дає\(\sqrt{a^2+x^2}=\sqrt{a^2+(a\tan θ)^2}=\sqrt{a^2(1+\tan^2θ)}=\sqrt{a^2sec^2θ}=|a\sec θ|=a\sec θ.\) (Оскільки\(−\dfrac{π}{2}<θ<\dfrac{π}{2}\) і\(\sec θ>0\) протягом цього інтервалу,\(|a\sec θ|=a\sec θ\).)
- Спростити вираз.
- Оцініть інтеграл за допомогою прийомів з розділу про тригонометричні інтеграли.
- Використовуйте опорний трикутник з\(\PageIndex{4}\) Figure, щоб переписати результат через\(x\). Можливо, вам також доведеться використовувати деякі тригонометричні ідентичності та відносини\(θ=\tan^{−1}\left(\dfrac{x}{a}\right)\). (Примітка: Опорний трикутник базується на припущенні, що\(x>0\); однак тригонометричні співвідношення, отримані з еталонного трикутника, такі ж, як і співвідношення для якого\(x≤0\).)
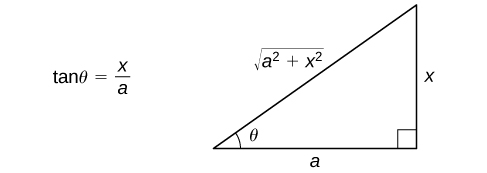
Оцініть\(\displaystyle ∫\dfrac{dx}{\sqrt{1+x^2}}\) і перевірте рішення шляхом диференціації.
Рішення
Починають з підміни\(x=\tan θ\) і\(dx=sec^2θ\,dθ\). Оскільки\(\tan θ=x\), намалюйте опорний трикутник на малюнку\(\PageIndex{5}\).
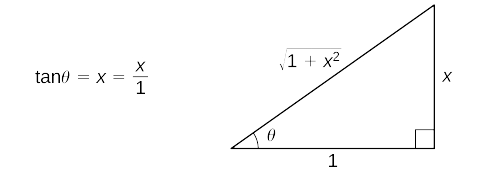
Таким чином,
\ (\ стиль відображення\ почати {вирівнювати*}\ dfrac {dx} {\ sqrt {1+x^2}} &=\ dfrac {\ сек^2θ} {\ сек θ} dθ &\ текст {Заміна} x =\ tan θ\ текст {і} dx=\ сек^2θ\, dθ.\\ [4pt]
&\ текст {Це заміна робить}\ sqrt {1+x^2} =\ сек θ. \ text {Спрощення.}\\ [4pt]
&=\ сек θ\, dθ & &\ text {Оцінити інтеграл.}\\ [4pt]
&=\ ln |\ сек θ +\ tan θ |+C & &\ text {Використовуйте еталонний трикутник, щоб висловити результат через} x.\\ [4pt]
&=\ ln |\ sqrt {1+x^2} +x|+C\ end {вирівнювати*}\)
Щоб перевірити рішення, диференціюйте:
\(\dfrac{d}{dx}\Big( \ln |\sqrt{1+x^2}+x|\Big)=\dfrac{1}{\sqrt{1+x^2}+x}⋅\left(\dfrac{x}{\sqrt{1+x^2}}+1\right) =\dfrac{1}{\sqrt{1+x^2}+x}⋅\dfrac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}}=\dfrac{1}{\sqrt{1+x^2}}.\)
Так як\(\sqrt{1+x^2}+x>0\) для всіх значень\(x\), ми могли б переписати\( \ln |\sqrt{1+x^2}+x|+C= \ln (\sqrt{1+x^2}+x)+C\), при бажанні.
Використовуйте підміну\(x=\sinh θ\) для оцінки\(\displaystyle ∫\dfrac{dx}{\sqrt{1+x^2}}.\)
Рішення
Тому що\(\sinh θ\) має діапазон всіх дійсних чисел, і\(1+\sinh^2θ=\cosh^2θ\), ми також можемо використовувати підстановку\(x=\sinh θ\) для оцінки цього інтеграла. В цьому випадку,\(dx=\cosh θ \,dθ.\) отже,
\ (\ стиль відображення\ почати {вирівнювати*}\ dfrac {dx} {\ sqrt {1+x^2}} &=\ dfrac {\ cosh θ} {\ sqrt {1+\ sinh^2θ}} dθ & &\ текст {Заміна} x =\ sinh θ\ текст {і} dx=\ cosh θ\, dθ\\\ 4 pt]
& &\ текст {Заміна} 1+\ sinh^2θ =\ кош ^ 2θ.\\ [4pt]
&=\ dfrac {\ кош θ} {\ sqrt {\ cosh^2θ}} dθ & амп; &\ текст {Починаючи з}\ sqrt {\ кош ^2θ} =|\ кош θ |\\ [4пт]
&=\ dfrac {\ кош θ} {|\ кош θ |} dθ & |\ кош θ | =\ кош θ\ текст {так}\ кош θ > 0\ текст {для всіх} θ.\\ [4pt]
=\ dfrac {\ cosh θ} {\ cosh θ} dθ & &\ текст {спростити.}\\ [4pt]
&= 1\, dθ & & \ text {Оцінити інтеграл.}\\ [4pt]
&=+C &\ text {Оскільки} x =\ sinh θ,\ текст {ми знаємо} θ =\ sinh^ {−1} x.\\ [4pt]
&=\ sinh^ {−1} x+c.\ end {align*}\)
Аналіз
Ця відповідь виглядає зовсім інакше, ніж відповідь, отримана за допомогою підміни\(x=\tan θ.\) Щоб побачити, що рішення однакові, задайте\(y=\sinh^{−1}x\). Таким чином,\(\sinh y=x.\) з цього рівняння отримуємо:
\[\dfrac{e^y−e^{−y}}{2}=x. \nonumber \]
Після множення обох сторін на\(2e^y\) і перезапису це рівняння стає:
\[e^{2y}−2xe^y−1=0. \nonumber \]
Використовуйте квадратне рівняння для вирішення для\(e^y\):
\[e^y=\dfrac{2x±\sqrt{4x^2+4}}{2}. \nonumber \]
Спрощуючи, ми маємо:
\[e^y=x±\sqrt{x^2+1}. \nonumber \]
Оскільки\(x−\sqrt{x^2+1}<0\), це повинно бути так\(e^y=x+\sqrt{x^2+1}\). Таким чином,
\[y= \ln (x+\sqrt{x^2+1}). \nonumber \]
Останній, отримуємо
\[\sinh^{−1}x= \ln (x+\sqrt{x^2+1}). \nonumber \]
Після ми зробимо остаточне зауваження, що, оскільки\(x+\sqrt{x^2+1}>0,\)
\[ \ln (x+\sqrt{x^2+1})= \ln ∣\sqrt{1+x^2}+x∣, \nonumber \]
ми бачимо, що два різних методи виробляють еквівалентні рішення.
Знайти довжину кривої\(y=x^2\) за інтервал\([0,\dfrac{1}{2}]\).
Рішення
\(\dfrac{dy}{dx}=2x\)Тому що довжина дуги задається
\[∫^{1/2}_0\sqrt{1+(2x)^2}dx=∫^{1/2}_0\sqrt{1+4x^2}dx. \nonumber \]
Щоб оцінити цей інтеграл, використовують заміщення\(x=\dfrac{1}{2}\tan θ\) і\(dx=\tfrac{1}{2}\sec^2θ \, dθ\). Нам також потрібно змінити межі інтеграції. Якщо\(x=0\), то\(θ=0\) і якщо\(x=\dfrac{1}{2}\), то\(θ=\dfrac{π}{4}.\) таким чином,
\(∫^{1/2}_0\sqrt{1+4x^2}dx=∫^{π/4}_0\sqrt{1+\tan^2θ}\cdot \tfrac{1}{2}\sec^2θ \, dθ\)Після підміни,\(\sqrt{1+4x^2}=\sec θ\). (Підставити\(1+\tan^2θ=\sec^2θ\) і спростити.)
\(=\tfrac{1}{2}∫^{π/4}_0\sec^3θ \, dθ\)Цей інтеграл ми вивели в попередньому розділі.
\(=\tfrac{1}{2}(\dfrac{1}{2}\sec θ\tan θ+ \dfrac{1}{2}\ln |\sec θ+\tan θ|)∣^{π/4}_0\)Оцінити і спростити.
\(=\tfrac{1}{4}(\sqrt{2}+ \ln (\sqrt{2}+1)).\)
Перепишіть\(\displaystyle ∫ x^3\sqrt{x^2+4}dx\) за допомогою підміни за участю\(\tan θ\).
- Підказка
-
Використання\(x=2\tan θ\) і\(dx=2\sec^2θ \, dθ.\)
- Відповідь
-
\[ ∫ 32\tan^3θ\sec^3θ \, dθ \nonumber \]
Інтеграція виразів за участю\(\sqrt{x^2−a^2}\)
Доменом виразу\(\sqrt{x^2−a^2}\) є\((−∞,−a]∪[a,+∞)\). Таким чином,\(x\le −a\) або\(x\ge a.\) Звідси,\(\dfrac{x}{a}≤−1\) або\(\dfrac{x}{a}≥1\). Оскільки ці інтервали відповідають діапазону\(\sec θ\) на\([0,\dfrac{π}{2})∪(\dfrac{π}{2},π]\) безлічі, має сенс використовувати підміну\(\sec θ=\dfrac{x}{a}\) або, що еквівалентно\(x=a\sec θ\), де\(0≤θ<\dfrac{π}{2}\) або\(\dfrac{π}{2}<θ≤π\). Відповідна заміна на\(dx\) є\(dx=a\sec θ\tan θ \, dθ\). Порядок використання цієї заміни викладено в наступній стратегії вирішення проблем.
- Перевірте, чи не можна оцінити інтеграл іншим методом. Якщо так, ми можемо розглянути можливість застосування альтернативної техніки.
- Замінник\(x=a\sec θ\) і\(dx=a\sec θ\tan θ \, dθ\). Ця\[ \sqrt{x^2−a^2}=\sqrt{(a\sec θ)^2−a^2}=\sqrt{a^2(\sec^2θ-1)}=\sqrt{a^2\tan^2θ}=|a\tan θ|. \nonumber \] заміна дає For\(x≥a, |a\tan θ|=a\tan θ\) і для\(x≤−a, |a\tan θ|=−a\tan θ.\)
- Спростити вираз.
- Оцініть інтеграл за допомогою прийомів з розділу про тригонометричні інтеграли.
- Використовуйте еталонні трикутники з Figure,\(\PageIndex{6}\) щоб переписати результат у терміні\(x\).
- Можливо, вам також доведеться використовувати деякі тригонометричні ідентичності та відносини\(θ=\sec^{−1}\left(\dfrac{x}{a}\right)\). (Примітка: Нам потрібні обидва опорні трикутники, оскільки значення деяких тригонометричних співвідношень відрізняються залежно від того, чи\(x>a\) чи\(x<−a\).)
Знайти площу області між графіком\(f(x)=\sqrt{x^2−9}\) і віссю x за інтервалом\([3,5].\)
Рішення
Спочатку намалюйте приблизний графік області, описаної в задачі, як показано на наступному малюнку.
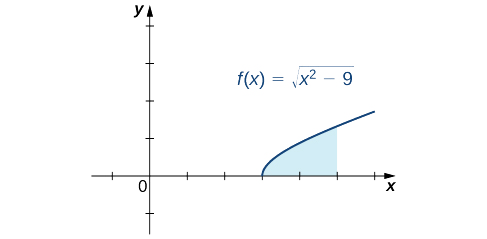
Ми бачимо, що площа є\(A=∫^5_3\sqrt{x^2−9}dx\). Щоб оцінити цей певний інтеграл,\(x=3\sec θ\) підставляють і\(dx=3\sec θ\tan θ \, dθ\). Ми також повинні змінити межі інтеграції. Якщо\(x=3\), то\(3=3\sec θ\) і значить\(θ=0\). Якщо\(x=5\), то\(θ=\sec^{−1}(\dfrac{5}{3})\). Зробивши ці заміни та спростивши, ми маємо
Площа\(=∫^5_3\sqrt{x^2−9}dx\)
\(=∫^{\sec^{−1}(5/3)}_09\tan^2θ\sec θ \, dθ\)Використовувати\(\tan^2θ=\sec^2θ - 1.\)
\(=∫^{\sec^{−1}(5/3)}_09(\sec^2θ−1)\sec θ \, dθ\)Розгорнути.
\(=∫^{\sec^{−1}(5/3)}_09(\sec^3θ−\sec θ)\,dθ\)Оцініть інтеграл.
\(=(\dfrac{9}{2} \ln |\sec θ+\tan θ|+\dfrac{9}{2}\sec θ\tan θ)−9 \ln |\sec θ+\tan θ|∣^{\sec^{−1}(5/3)}_0\)Спростити.
\(=\dfrac{9}{2}\sec θ\tan θ−\dfrac{9}{2} \ln |\sec θ+\tan θ|∣^{\sec^{−1}(5/3)}_0\)Оцінити. Використання\(\sec(\sec^{−1}\dfrac{5}{3})=\dfrac{5}{3}\) і\(\tan(\sec^{−1}\dfrac{5}{3})=\dfrac{4}{3}.\)
\(=\dfrac{9}{2}⋅\dfrac{5}{3}⋅\dfrac{4}{3}−\dfrac{9}{2} \ln ∣\dfrac{5}{3}+\dfrac{4}{3}∣−(\dfrac{9}{2}⋅1⋅0−\dfrac{9}{2} \ln |1+0|)\)
\(=10−\dfrac{9}{2} \ln 3\)
Оцініть\[∫\dfrac{dx}{\sqrt{x^2−4}}. \nonumber \] Припустимо, що\(x>2.\)
- Підказка
-
Замінник\(x=2\sec θ\) і\(dx=2\sec θ\tan θ \, dθ.\)
- Відповідь
-
\[ \ln |\dfrac{x}{2}+\dfrac{\sqrt{x^2−4}}{2}|+C \nonumber \]
Ключові концепції
- Для інтегралів за\(\sqrt{a^2−x^2}\) участю використовують підстановку\(x=a\sin θ\) і\(dx=a\cos θ \, dθ.\)
- Для інтегралів за\(\sqrt{a^2+x^2}\) участю використовують підстановку\(x=a\tan θ\) і\(dx=a\sec^2θ \, dθ\).
- Для інтегралів за участю\(\sqrt{x^2−a^2}\)\(x=a\sec θ\) підставляють і\(dx=a\sec θ\tan θ \,dθ\).
Глосарій
- тригонометрична заміна
- метод інтеграції, який перетворює алгебраїчний інтеграл, що містить вирази форми\(\sqrt{a^2−x^2}\)\(\sqrt{a^2+x^2}\), або\(\sqrt{x^2−a^2}\) в тригонометричний інтеграл
