7.6: Чисельна інтеграція
- Page ID
- 62140
- Наближення значення певного інтеграла можна за допомогою середніх і трапецієподібних правил.
- Визначте абсолютну і відносну похибку при використанні методики числового інтегрування.
- Оцініть абсолютну та відносну похибку за допомогою формули, пов'язаної з помилкою.
- Визнайте, коли середина та трапецієподібні правила над- або занижують істинне значення інтеграла.
- Використовуйте правило Сімпсона, щоб наблизити значення певного інтеграла до заданої точності.
Антипохідні багатьох функцій або не можуть бути виражені, або не можуть бути легко виражені в замкнутому вигляді (тобто з точки зору відомих функцій). Отже, замість того, щоб безпосередньо оцінювати певні інтеграли цих функцій, ми вдаємося до різних методів числового інтегрування для наближення їх значень. У цьому розділі ми вивчимо кілька з цих прийомів. Крім того, ми вивчаємо процес оцінки похибки при використанні цих методик.
Правило середньої точки
Раніше в цьому тексті визначено певний інтеграл функції через інтервал як межу сум Рімана. Загалом, будь-яка сума Рімана функції\( f(x)\) за інтервалом\([a,b]\) може розглядатися як оцінка\(\displaystyle ∫^b_af(x)\,dx\). Нагадаємо, що сума Рімана функції\( f(x)\) за інтервалом\( [a,b]\) отримується шляхом вибору розділу
\[ P=\{x_0,x_1,x_2,…,x_n\} \nonumber \]
де\(\quad a=x_0<x_1<x_2<⋯<x_n=b \)
і набір
\[ S=\{x^*_1,x^*_2,…,x^*_n\} \nonumber \]
де\(x_{i−1}≤x^*_i≤x_i \quad \text{for all} \, i.\)
Сума Рімана, що відповідає розділенню\(P\) та множині\(\displaystyle \sum^n_{i=1}f(x^*_i)Δx_i\),\(S\) задається\( Δx_i=x_i−x_{i−1},\) тим, де довжина\( i^{\text{th}}\) підінтервалу.
Правило середньої точки для оцінки певного інтеграла використовує суму Рімана з підінтервалами однакової ширини та\( m_i\) середніми точками кожного підінтервалу замість\( x^*_i\). Формально ми викладемо теорему щодо збіжності правила середньої точки наступним чином.
Припустімо,\( f(x)\) що безперервно на\([a,b]\). \( n\)Дозволяти бути натуральним числом і\( Δx=\dfrac{b−a}{n}\). Якщо\( [a,b]\) ділиться на\( n\) підінтервали, кожен довжини\( Δx\), і\( m_i\) є середньою точкою\( i^{\text{th}}\) підінтервалу, встановленого
\[M_n=\sum_{i=1}^nf(m_i)Δx. \nonumber \]
Тоді\(\displaystyle \lim_{n→∞}M_n=∫^b_af(x)\,dx.\)
Як ми бачимо на малюнку\(\PageIndex{1}\), якщо\( f(x)≥0\) закінчено\( [a,b]\), то\(\displaystyle \sum^n_{i=1}f(m_i)Δx\) відповідає сума площ прямокутників, що наближають площу між графіком\( f(x)\) і\(x\) -віссю над\([a,b]\). На графіку показані прямокутники, що відповідають\(M_4\) невід'ємній функції за замкнутий інтервал\([a,b].\)
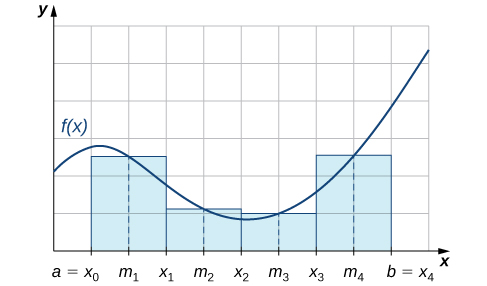
Використовуйте правило середньої точки для оцінки за\(\displaystyle ∫^1_0x^2\,dx\) допомогою чотирьох підінтервалів. Порівняйте результат з фактичним значенням цього інтеграла.
Рішення: Кожен підінтервал має довжину\( Δx=\dfrac{1−0}{4}=\dfrac{1}{4}.\) Тому підінтервали складаються з
\[\left[0,\tfrac{1}{4}\right],\,\left[\tfrac{1}{4},\tfrac{1}{2}\right],\,\left[\tfrac{1}{2},\tfrac{3}{4}\right],\, \text{and}\, \left[\tfrac{3}{4},1\right].\nonumber \]
Середні точки цих підінтервалів є\(\left\{\frac{1}{8},\,\frac{3}{8},\,\frac{5}{8},\, \frac{7}{8}\right\}.\) Таким чином,
\[\begin{align*} M_4 &=\frac{1}{4}\cdot f\left(\frac{1}{8}\right)+\frac{1}{4}\cdot f\left(\frac{3}{8}\right)+\frac{1}{4}\cdot f\left(\frac{5}{8}\right)+\frac{1}{4}\cdot f\left(\frac{7}{8}\right) \\[4pt] &=\frac{1}{4}⋅\frac{1}{64}+\frac{1}{4}⋅\frac{9}{64}+\frac{1}{4}⋅\frac{25}{64}+\frac{1}{4}⋅\frac{49}{64}\\[4pt] &=\frac{21}{64} = 0.328125. \end{align*}\]
Так як
\[ ∫^1_0x^2\,dx=\frac{1}{3},\nonumber \]
абсолютна похибка в цьому наближенні дорівнює:
\[\left\lvert\dfrac{1}{3}−\dfrac{21}{64}\right\rvert=\dfrac{1}{192}≈0.0052, \nonumber \]
і ми бачимо, що правило середньої точки виробляє оцінку, яка дещо близька до фактичного значення певного інтеграла.
\(M_6\)Використовується для оцінки довжини кривої\(y=\frac{1}{2}x^2\) на\([1,4]\).
Рішення: Довжина\(y=\frac{1}{2}x^2\)\([1,4]\) на
\[s = ∫^4_1\sqrt{1+\left(\frac{dy}{dx}\right)^2}\,dx.\nonumber \]
З тих пір\(\dfrac{dy}{dx}=x\), цей невід'ємний стає\(\displaystyle ∫^4_1\sqrt{1+x^2}\,dx.\)
Якщо\([1,4]\) розділити на шість підінтервалів, то кожен підінтервал має довжину,\(Δx=\dfrac{4−1}{6}=\dfrac{1}{2}\) а середні точки підінтервалів -\(\left\{\frac{5}{4},\frac{7}{4},\frac{9}{4},\frac{11}{4},\frac{13}{4},\frac{15}{4}\right\}\). Якщо ми встановимо\(f(x)=\sqrt{1+x^2}\),
\[\begin{align*} M_6 &=\tfrac{1}{2}\cdot f\left(\frac{5}{4}\right)+\tfrac{1}{2}\cdot f\left(\frac{7}{4}\right)+\frac{1}{2}\cdot f\left(\frac{9}{4}\right)+\frac{1}{2}\cdot f\left(\frac{11}{4}\right)+\frac{1}{2}\cdot f\left(\frac{13}{4}\right)+\frac{1}{2}\cdot f\left(\frac{15}{4}\right) \\[4pt] &≈\frac{1}{2}(1.6008+2.0156+2.4622+2.9262+3.4004+3.8810)=8.1431 \, \text{ units}. \end{align*}\]
Використовуйте правило середньої точки with\( n=2\) для оцінки\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Підказка
-
\( Δx=\frac{1}{2}, \quad m_1=\frac{5}{4},\quad \text{and} \quad m_2=\frac{7}{4}.\)
- Відповідь
-
\(\dfrac{24}{35}\approx 0.685714\)
Трапецієподібне правило
Ми також можемо наблизити значення певного інтеграла, використовуючи трапеції, а не прямокутники. На\(\PageIndex{2}\) малюнку область під кривою наближена трапеціями, а не прямокутниками.
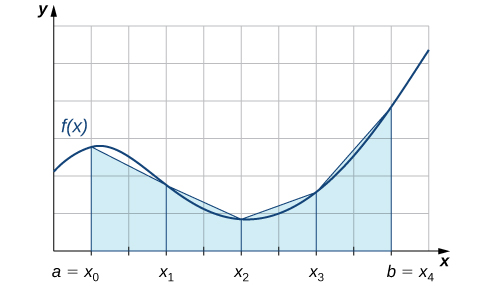
Трапецієподібне правило для оцінки певних інтегралів використовує трапеції, а не прямокутники для наближення площі під кривою. Щоб отримати уявлення про остаточну форму правила, розглянемо трапеції, зображені на малюнку\(\PageIndex{2}\). Припустимо, що довжина кожного підінтервалу задана\(Δx\). По-перше, нагадаємо, що площа трапеції з висотою\(h\) і\(b_1\) підстави довжини і\(b_2\) задається\(\text{Area}=\frac{1}{2}h(b_1+b_2)\). Бачимо, що перша трапеція має висоту\(Δx\) і паралельні\( f(x_0)\) підстави довжини і\( f(x_1)\). Таким чином, площа першої трапеції на малюнку\(\PageIndex{2}\) дорівнює
\[ \frac{1}{2}Δx\Big(f(x_0)+f(x_1)\Big).\nonumber \]
Ділянки решти трьох трапецій
\(\dfrac{1}{2}Δx\Big(f(x_1)+f(x_2)\Big),\, \dfrac{1}{2}Δx\Big(f(x_2)+f(x_3)\Big),\)і\( \dfrac{1}{2}Δx\Big(f(x_3)+f(x_4)\Big).\)
Отже,
\[∫^b_af(x)\,dx≈\frac{1}{2}Δx\Big(f(x_0)+f(x_1)\Big)+\frac{1}{2}Δx\Big(f(x_1)+f(x_2)\Big)+\frac{1}{2}Δx\Big(f(x_2)+f(x_3)\Big)+\frac{1}{2}Δx\Big(f(x_3)+f(x_4)\Big).\nonumber \]
Вийнявши загальний фактор\(\frac{1}{2}Δx\) і об'єднавши подібні терміни, ми маємо
\[ ∫^b_af(x)\,dx≈\frac{Δx}{2}\Big[f(x_0)+2\,f(x_1)+2\,f(x_2)+2\,f(x_3)+f(x_4)\Big].\nonumber \]
Узагальнюючи, формально викласти наступне правило.
Припустимо,\(f(x)\) що безперервно закінчується\([a,b]\). \(n\)Дозволяти бути натуральним числом і\(Δx=\dfrac{b−a}{n}\). \( [a,b]\)Дозволяти розділити на\(n\) підінтервали, кожен довжини\(Δx\), з кінцевими точками на\( P=\{x_0,x_1,x_2…,x_n\}.\)
Набір
\[T_n=\frac{Δx}{2}\Big[f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_{n−1})+f(x_n)\Big]. \nonumber \]
Потім,\(\displaystyle \lim_{n→+∞}T_n=∫^b_af(x)\,dx.\)
Перш ніж продовжити, зробимо кілька спостережень щодо трапецієподібного правила. Перш за все, корисно відзначити, що
\(T_n=\dfrac{1}{2}(L_n+R_n)\)де\(\displaystyle L_n=\sum_{i=1}^nf(x_{i−1})Δx\) і\(\displaystyle R_n=\sum_{i=1}^nf(x_i)Δx.\)
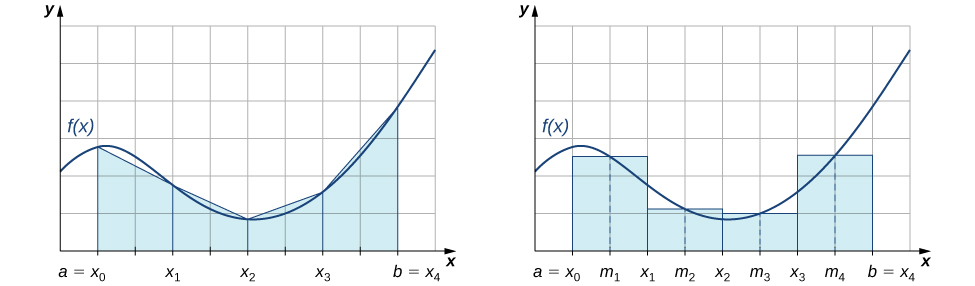
Тобто\(L_n\) і\(R_n\) наближають інтеграл, використовуючи ліву і праву кінцеві точки кожного підінтервалу відповідно. Крім того, ретельне вивчення Figure\(\PageIndex{3}\) змушує нас зробити наступні спостереження щодо використання трапецієподібних правил та правил середньої точки для оцінки певного інтеграла невід'ємної функції. Трапецієподібне правило має тенденцію переоцінювати значення певного інтеграла систематично протягом інтервалів, де функція увігнута вгору, і занижувати значення певного інтеграла систематично протягом інтервалів, де функція увігнута вниз. З іншого боку, правило середньої точки, як правило, дещо усереднює ці помилки, частково завищуючи та частково занижуючи значення певного інтеграла над цими самими типами інтервалів. Це призводить нас до гіпотези, що в цілому правило середньої точки має тенденцію бути більш точним, ніж трапецієподібне правило.
Використовуйте трапецієподібне правило для оцінки\(\displaystyle ∫^1_0x^2\,dx\) за допомогою чотирьох підінтервалів.
Рішення
Кінцеві точки підінтервалів складаються з елементів множини\(P=\left\{0,\frac{1}{4},\, \frac{1}{2},\, \frac{3}{4},1\right\}\) і\(Δx=\frac{1−0}{4}=\frac{1}{4}.\) Таким чином,
\ [\ begin {align*} ^1_0x^2dx &≈\ frac {1} {2} ⋅ відрив {1} {4}\ Великий [f (0) +2\, f\ лівий (\ tfrac {1} {1}\ правий) +2\, f\ лівий (\ tfrac {1} {2}\ праворуч) +2\ лівий (\ tfrac {1}\ правий) +2\ лівий (\ tfrac {1}\ правий) +2\ лівий (\ tfrac c {3} {4}\ право) +f (1)\ Великий]\\ [4pt]
&=\ trac {1} {8}\ великий (0+2⋅\ trac {1} {16} +2⋅\ trac {1} {4} +2⋅\ trac {9} {16} +1\ великий)\\[4pt] &=\frac{11}{32} = 0.34375\end{align*}\]
Використовуйте трапецієподібне правило з\( n=2\) для оцінки\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Підказка
-
\(Δx=\dfrac{1}{2}.\)Встановити Кінцеві точки підінтервалів є елементами множини\(P=\left\{1,\frac{3}{2},2\right\}.\)
- Відповідь
-
\(\dfrac{17}{24} \approx 0.708333\)
Абсолютна і відносна похибка
Важливим аспектом використання цих числових правил наближення є обчислення похибки їх використання для оцінки значення певного інтеграла. Спочатку потрібно визначити абсолютну похибку і відносну похибку.
Якщо\(B\) наша оцінка деякої величини має фактичне значення\(A\), то абсолютна похибка задається шляхом\(|A−B|\).
Відносна похибка - це похибка у відсотках від фактичного значення і задається\[\left\lvert\frac{A−B}{A}\right\rvert⋅100\%. \nonumber \]
Обчисліть абсолютну та відносну похибку в оцінці\(\displaystyle ∫^1_0x^2\,dx\) використання правила середньої точки, знайденого в прикладі\(\PageIndex{1}\).
Рішення: Розраховане значення є\(\displaystyle ∫^1_0x^2\,dx=\frac{1}{3}\) і наша оцінка з прикладу є\(M_4=\frac{21}{64}\). Таким чином, абсолютна похибка задається\(\left\lvert\frac{1}{3}−\frac{21}{64}\right\rvert=\frac{1}{192}≈0.0052.\)
Відносна похибка:\[\frac{1/192}{1/3}=\frac{1}{64}≈0.015625≈1.6\%.\nonumber \]
Обчислити абсолютну і відносну похибку в оцінці\(\displaystyle ∫^1_0x^2\,dx\) за допомогою трапецієподібного правила, знайденого в прикладі\(\PageIndex{3}\).
Рішення: Розраховане значення є\(\displaystyle ∫^1_0x^2\,dx=\frac{1}{3}\) і наша оцінка з прикладу є\(T_4=\frac{11}{32}\). Таким чином, абсолютна похибка задається\(\left\lvert\frac{1}{3}−\frac{11}{32}\right\rvert=\frac{1}{96}≈0.0104.\)
Відносна похибка задається\[\frac{1/96}{1/3}=0.03125≈3.1\%.\nonumber \]
У більш ранньому контрольно-пропускному пункті, за\(\displaystyle ∫^2_1\frac{1}{x}\,dx\) оцінками, буде\(\frac{24}{35}\) використано\(M_2\). Фактичне значення цього інтеграла дорівнює\(\ln 2\). Використовуючи\(\frac{24}{35}≈0.6857\) і\(\ln 2≈0.6931,\) обчислити абсолютну похибку і відносну похибку.
- Підказка
-
Використовуйте попередні приклади як орієнтир.
- Відповідь
-
абсолютна похибка\(\approx 0.0074,\) і відносна похибка\(\approx 1.1\%\)
Межі помилок на середніх і трапецієподібних правилах
У двох попередніх прикладах ми змогли порівняти нашу оцінку інтеграла з фактичним значенням інтеграла; однак, ми зазвичай не маємо цієї розкоші. Загалом, якщо ми наближаємо інтеграл, ми робимо це, тому що ми не можемо обчислити точне значення самого інтеграла легко. Тому часто корисно вміти визначити верхню межу помилки в наближенні інтеграла. Наступна теорема дає межі похибки для середніх та трапецієподібних правил. Теорема викладена без доказів.
\(f(x)\)Дозволяти безперервна функція над\([a,b]\), маючи другу похідну\(f''(x)\) протягом цього інтервалу. Якщо\(M\) є максимальним значенням\(|f''(x)|\) понад\([a,b]\), то верхні межі помилки у використанні\(M_n\) та\(T_n\) оцінці\(\displaystyle ∫^b_af(x)\,dx\) є
\[\text{Error in}\, M_n≤\frac{M(b−a)^3}{24n^2}\label{MidError} \]
і
\[\text{Error in}\, T_n≤\frac{M(b−a)^3}{12n^2} \nonumber \].
Ми можемо використовувати ці межі, щоб визначити значення,\(n\) необхідне, щоб гарантувати, що похибка в оцінці менше зазначеного значення.
Яке значення\(n\) має бути використано, щоб гарантувати, що оцінка\(\displaystyle ∫^1_0e^{x^2}\,dx\) є точною в межах,\(0.01\) якщо ми використовуємо правило середньої точки?
Рішення
Починаємо з визначення значення\(M\), максимальне значення\( |f''(x)|\) понад\( [0,1]\) для\( f(x)=e^{x^2}\). Так як у\( f′(x)=2xe^{x^2},\) нас є
\[ f''(x)=2e^{x^2}+4x^2e^{x^2}.\nonumber \]
Таким чином,
\[ |f''(x)|=2e^{x^2}(1+2x^2)≤2⋅e⋅3=6e.\nonumber \]
З рівняння\(\ref{MidError}\), пов'язаного з помилкою, ми маємо
\[ \text{Error in}\, M_n≤\frac{M(b−a)^3}{24n^2}≤\frac{6e(1−0)^3}{24n^2}=\frac{6e}{24n^2}.\nonumber \]
Тепер вирішимо наступне нерівність для\(n\):
\[\frac{6e}{24n^2}≤0.01.\nonumber \]
Таким чином,\(n≥\sqrt{\frac{600e}{24}}≈8.24.\) Оскільки\(n\) має бути цілим числом, що задовольняє цю нерівність, вибір\(n=9\) буде гарантувати, що
\[ \left\lvert ∫^1_0e^{x^2}\,dx−M_n \right\rvert <0.01.\nonumber \]
Аналіз
Ми могли б бути спокуса округлити\(8.24\) вниз і вибрати\(n=8\), але це було б неправильно, тому що ми повинні мати ціле число більше або дорівнює\(8.24\). Потрібно мати на увазі, що оцінки помилок забезпечують верхню межу тільки для помилки. Фактична оцінка може бути, насправді, набагато кращим наближенням, ніж вказує прив'язка до помилки.
Використовуйте Рівняння,\(\ref{MidError}\) щоб знайти верхню межу помилки при використанні\(M_4\) для оцінки\(\displaystyle ∫^1_0x^2\,dx.\)
- Підказка
-
\(f''(x)=2,\)так\(M=2.\)
- Відповідь
-
\(\dfrac{1}{192}\)
Правило Сімпсона
За допомогою правила середньої точки ми оцінили площі областей під кривими за допомогою прямокутників. У певному сенсі ми наблизили криву з кусково-постійними функціями. За допомогою трапецієподібного правила ми наблизили криву за допомогою кусково-лінійних функцій. Що робити, якби ми були, замість цього, щоб наблизити криву, використовуючи кусково-квадратичні функції? З правилом Сімпсона, ми робимо саме це. Розбиваємо інтервал на парну кількість підінтервалів, кожен однакової ширини. Над першою парою підінтервалів ми наближаємося\(\displaystyle ∫^{x_2}_{x_0}f(x)\,dx\) з\(\displaystyle ∫^{x_2}_{x_0}p(x)\,dx\), де\(p(x)=Ax^2+Bx+C\) - квадратична функція, що проходить через\((x_0,f(x_0)), \,(x_1,f(x_1)),\) і\((x_2,f(x_2))\) (рис.\(\PageIndex{4}\)). Протягом наступної пари підінтервалів ми наближаємося\(\displaystyle ∫^{x_4}_{x_2}f(x)\,dx\) інтегралом іншої квадратичної функції, що проходить через\( (x_2,f(x_2)), \,(x_3,f(x_3)),\) і\((x_4,f(x_4)).\) Цей процес продовжується з кожною наступною парою підінтервалів.
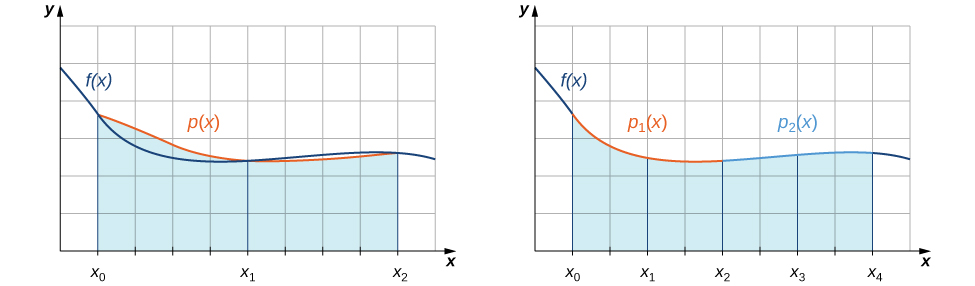
Щоб зрозуміти формулу, яку ми отримуємо для правила Сімпсона, ми починаємо з виведення формули для цього наближення протягом перших двох підінтервалів. Проходячи через деривацію, нам потрібно мати на увазі наступні відносини:
\[f(x_0)=p(x_0)=Ax_0^2+Bx_0+C \nonumber \]
\[f(x_1)=p(x_1)=Ax_1^2+Bx_1+C \nonumber \]
\[f(x_2)=p(x_2)=Ax_2^2+Bx_2+C \nonumber \]
\(x_2−x_0=2Δx\), Де\(Δx\) - довжина субінтервалу.
\(x_2+x_0=2x_1,\)так як\(x_1=\dfrac{(x_2+x_0)}{2}\).
Таким чином,
\ [\ почати {вирівнювати*} ^ {x_2} _ {x_0} f (x)\, дх &≈^ {x_2} _ {x_0} p (x)\, dx\\ [4pt]
&= ^ {x_2} _ {x_0} (ос^2+Вх+С)\, дх\\ [4пт]
&=\ =\ (\ розрив {A} {3} x^3+\ frac {B} {2} x^2+CX\ праворуч)\ bigg|^ {x_2} _ {x_0} &\ text {Знайти антипохідну.}\\ [4pt]
&=\ frac {A} {3} (x_2^3−x_0^3) +\ frac {B} {2} (x_2^2−x_0^2) +C (x_2−x_0) &\ text {Оцінити антипохідну.}\\ [4pt]
&=\ frac {A} {3} (x_2−x_0) (x_2^2+x_2x_0+x0^2) +\ frac {B} {2} (x_2−x_0) (x_2+x_0) +C (x_2−x_0)\\ [4pt]
&=\ розрив {x_2−x_0} {6}\ великий (2A (x_2^2+x_2x_0+x_0+x_0^2) +3B (x_2+x_0) +6C\ великий) &\ текст {фактор вихід}\,\ розрив {x_2−x_0} {6}.\\ [4pt]
&=\ розрив {Δx} {3}\ великий ((Ax_2^2+Bx_2+C) + (Ax_0^2+Bx_0+C) +A (x_2^2+2x_2x_0+x_0^2) +2B (x_2+x_0) +4C\ bigg) &\ text {Перевпорядкувати терміни. Примітка:}\ простір Δx =\ розрив {x_2−x_0} {2}\\ [4pt]
&=\ розрив {Δx} {3}\ великий (f (x_2) +f (x_0) +A (x_2+x_0) ^2+2B (x_2+x_0) +4C\ великий) &\ текст {Фактор і замінити:}\\ [4pt]
& &\ quad f (x_2) =Ax_2^2+Bx_2+C\ пробіл {і}\ пробіл f (x_0) =Ax_0^2+Bx_0+C.\\ [4pt]
&=\ розрив {Δx} {3}\ великий (f (x_2) +f (x_0) +A (2x_1) ^2+2B (2x_1) +4C\ великий) &\ текст {Заміна}\, x_2+x_0 = 2x_1.\\ [4pt]
& &\ quad\ текст {Примітка:}\ x_1.\\ [4pt] & &\ quad\ текст {Примітка:}\ x_1 =\ frac {x_2+x_0} {2}\ простір\ текст {є серединою.}\\ [4pt]
&=\ розрив {Δx} {3}\ великий (f (x_2) +4f (x_1) +f (x_0)\ великий). &\ текст {Розгорнути і замінити}\, f (x_1) =Ax_1^2+Bx_1+C.\ end {align*}\]
Якщо ми наближаємося\(\displaystyle ∫^{x_4}_{x_2}f(x)\,dx\) за допомогою того ж методу, ми бачимо, що у нас є
\[∫^{x_4}_{x_2}f(x)\,dx≈\frac{Δx}{3}(f(x_4)+4\,f(x_3)+f(x_2)).\nonumber \]
Поєднавши ці два наближення, отримаємо
\[∫^{x_4}_{x_0}f(x)\,dx≈\frac{Δx}{3}(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+f(x_4)).\nonumber \]
Візерунок продовжується, коли ми додаємо пари підінтервалів до нашого наближення. Загальне правило може бути викладено наступним чином.
Припустимо,\(f(x)\) що безперервно закінчується\([a,b]\). \(n\)Дозволяти бути додатним парним числом і\(Δx=\dfrac{b−a}{n}\). \([a,b]\)Дозволяти розділити на\(n\) підінтервали, кожен довжини\(Δx\), з кінцевими точками на\(P=\{x_0,x_1,x_2,…,x_n\}.\) Set
\[S_n=\frac{Δx}{3}\Big[f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\Big]. \nonumber \]
Потім,
\[\lim_{n→+∞}S_n=∫^b_af(x)\,dx.\nonumber \]
Подібно до того, як трапецієподібне правило є середнім з лівих і правих правил для оцінки певних інтегралів, правило Сімпсона може бути отримано з середньої точки і трапецієподібних правил, використовуючи середньозважене значення. Це можна показати, що\(S_{2n}=\left(\frac{2}{3}\right)M_n+\left(\frac{1}{3}\right)T_n\).
Також можна поставити прив'язку до помилки при використанні правила Сімпсона для наближення певного інтеграла. Прив'язка в помилку задається наступним правилом:
\(f(x)\)Дозволяти безперервна функція над\([a,b]\) мають четверту похідну\( f^{(4)}(x)\), протягом цього інтервалу. Якщо\(M\) є максимальним значенням\(∣f^{(4)}(x)∣\) понад\([a,b]\), то верхня межа помилки використання\(S_n\) для оцінки\(\displaystyle ∫^b_af(x)\,dx\) задається
\[\text{Error in}\, S_n≤\frac{M(b−a)^5}{180n^4}. \nonumber \]
Використовуйте\(S_2\) для наближення\(\displaystyle ∫^1_0x^3\,dx\). Оцінити прив'язку для помилки в\(S_2\).
Рішення
Так як\([0,1]\) ділиться на два інтервали, кожен субінтервал має довжину\(Δx=\frac{1−0}{2}=\frac{1}{2}\). Кінцеві точки цих підінтервалів є\(\left\{0,\frac{1}{2},1\right\}\). Якщо ми встановимо,\(f(x)=x^3,\) то
\[S_2=\frac{1}{3}⋅\frac{1}{2}(f(0)+4\,f(\frac{1}{2})+f(1))=\frac{1}{6}(0+4⋅\frac{1}{8}+1)=\frac{1}{4}.\nonumber \]
Оскільки\( f^{(4)}(x)=0\) і, отже,\(M=0,\) ми бачимо, що
Помилка в\(S_2≤\frac{0(1)^5}{180⋅2^4}=0.\)
Ця межа вказує на те, що значення, отримане за допомогою правила Сімпсона, є точним. Швидка перевірка перевірить, що, власне,\(\displaystyle ∫^1_0x^3\,dx=\frac{1}{4}.\)
\(S_6\)Використовується для оцінки довжини\(y=\frac{1}{2}x^2\) кривої\([1,4].\)
Рішення
Довжина\(y=\frac{1}{2}x^2\) над\([1,4]\) є\(\displaystyle ∫^4_1\sqrt{1+x^2}\,dx\). Якщо\([1,4]\) розділити на шість підінтервалів, то кожен підінтервал має довжину\(Δx=\frac{4−1}{6}=\frac{1}{2}\), а кінцеві точки підінтервалів -\( \left\{1,\frac{3}{2},2,\frac{5}{2},3,\frac{7}{2},4\right\}.\) Setting\( f(x)=\sqrt{1+x^2}\),
\[S_6=\frac{1}{3}⋅\frac{1}{2}(f(1)+4f(\frac{3}{2})+2f(2)+4f(\frac{5}{2})+2f(3)+4f(\frac{7}{2})+f(4)).\nonumber \]
Після підміни ми маємо
\[S_6=\frac{1}{6}(1.4142+4⋅1.80278+2⋅2.23607+4⋅2.69258+2⋅3.16228+4⋅3.64005+4.12311)≈8.14594\,\text{units}. \nonumber \]
\(S_2\)Використовувати для оцінки\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Підказка
-
\[S_2=\frac{1}{3}Δx\left(f(x_0)+4f(x_1)+f(x_2)\right) \nonumber \]
- Відповідь
-
\(\frac{25}{36} \approx 0.694444\)
Ключові концепції
- Ми можемо використовувати числове інтегрування для оцінки значень визначених інтегралів, коли замкнуту форму інтеграла важко знайти або коли потрібно наближене значення лише певного інтеграла.
- Найбільш часто використовуваними методами числового інтегрування є правило середньої точки, трапецієподібне правило та правило Сімпсона.
- Правило середньої точки наближає певний інтеграл за допомогою прямокутних областей, тоді як правило трапеції наближає певний інтеграл за допомогою трапецієподібних наближень.
- Правило Сімпсона наближає певний інтеграл, спочатку наближаючи початкову функцію за допомогою кусково-квадратичних функцій.
Ключові рівняння
- Правило середньої точки
\(\displaystyle M_n=\sum^n_{i=1}f(m_i)Δx\)
- трапецієподібне правило
\(T_n=\frac{Δx}{2}\Big[f(x_0)+2\,f(x_1)+2\,f(x_2)+⋯+2\,f(x_{n−1})+f(x_n)\Big]\)
- правило Сімпсона
\(S_n=\frac{Δx}{3}\Big[f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+4\,f(x_5)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\Big]\)
- Помилка прив'язана до правила середньої точки
Помилка в\(M_n≤\dfrac{M(b−a)^3}{24n^2}\),\(M\) де максимальне значення\(|f''(x)|\) понад\([a,b]\).
- Помилка обмежена для трапецієподібного правила
Помилка в\(T_n≤\dfrac{M(b−a)^3}{12n^2}\),\(M\) де максимальне значення\(|f''(x)|\) понад\([a,b]\).
- Помилка пов'язана з правилом Сімпсона
Помилка в\(S_n≤\dfrac{M(b−a)^5}{180n^4}\),\(M\) де максимальне значення\(∣f^{(4)}(x)∣\) понад\([a,b]\).
Глосарій
- абсолютна похибка
- якщо\(B\) є оцінкою деякої величини, що має фактичне значення\(A\), то абсолютна похибка задається\( |A−B|\)
- правило середньої точки
- правило, яке використовує суму Рімана форми\(\displaystyle M_n=\sum^n_{i=1}f(m_i)Δx\), де\( m_i\) середина\(i^{\text{th}}\) підінтервалу для наближення\(\displaystyle ∫^b_af(x)\,dx\)
- числове інтегрування
- різноманітність числових методів, що використовуються для оцінки значення певного інтеграла, включаючи правило середньої точки, трапецієподібне правило та правило Сімпсона
- відносна помилка
- помилка у відсотках від фактичного значення, заданого\[\text{relative error}=\left|\frac{A−B}{A}\right|⋅100\%\nonumber \]
- правило Сімпсона
- правило, яке\(\displaystyle ∫^b_af(x)\,dx\) наближається за допомогою площі під кусково-квадратичною функцією.
Наближення\(S_n\) до\(\displaystyle ∫^b_af(x)\,dx\) задається\[S_n=\frac{Δx}{3}\big(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\big).\nonumber \]
- трапецієподібне правило
- правило, яке\(\displaystyle ∫^b_af(x)\,dx\) наближається за допомогою площі трапецій.
Наближення\(T_n\) до\(\displaystyle ∫^b_af(x)\,dx\) задається\[T_n=\frac{Δx}{2}\big(f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_{n−1})+f(x_n)\big).\nonumber \]
Автори та атрибуція
- Template:ContribOpenStaxCalc
- Edited by Paul Seeburger (Monroe Community College). Notes added to development of area under a parabola and typos fixed in original text.
