7.7: Неправильні інтеграли
- Page ID
- 62139
- Оцініть інтеграл через нескінченний інтервал.
- Оцініть інтеграл за замкнутий інтервал з нескінченним розривом всередині інтервалу.
- Використовуйте теорему порівняння, щоб визначити, чи збіжним є певний інтеграл.
Площа між графіком\(f(x)=\dfrac{1}{x}\) і\(x\) -віссю над інтервалом\([1,+∞)\) скінченна або нескінченна? Якщо ця ж область обертається навколо\(x\) -осі, об'єм кінцевий або нескінченний? Дивно, але площа описуваної області нескінченна, але обсяг твердого тіла, отриманого обертанням цієї області навколо\(x\) -осі, кінцевий.
У цьому розділі визначено інтеграли через нескінченний інтервал, а також інтеграли функцій, що містять розрив на інтервалі. Інтеграли цих типів називаються некоректними інтегралами. Ми розглядаємо кілька методів оцінки неправильних інтегралів, всі з яких передбачають обмеження.
Інтеграція через нескінченний інтервал
Як ми повинні йти про визначення інтеграла типу\(\displaystyle \int ^{+∞}_af(x)\,dx?\) Ми можемо інтегрувати\(\displaystyle \int ^t_af(x)\,dx\) для будь-якого значення\(t\), тому розумно дивитися на поведінку цього інтеграла, як ми підставляємо великі значення\(t\). \(\PageIndex{1}\)На малюнку показано, що\(\displaystyle \int ^t_af(x)\,dx\) можна інтерпретувати як область для різних значень\(t\). Іншими словами, ми можемо визначити неправильний інтеграл як ліміт, прийнятий як одна з меж інтеграції збільшується або зменшується без обмежень.

- \(f(x)\)Дозволяти бути безперервним протягом інтервалу форми\([a,+∞)\). Тоді\[\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx, \label{improper1} \] за умови, що цей ліміт існує.
- \(f(x)\)Дозволяти бути безперервним протягом інтервалу форми\((−∞,b]\). Тоді\[\int ^b_{−∞}f(x)\,dx=\lim_{t→−∞}\int ^b_tf(x)\,dx, \label{improper2} \] за умови, що цей ліміт існує.
У кожному випадку, якщо межа існує, то неправильний інтеграл, як кажуть, сходиться. Якщо межі не існує, то неправильний інтеграл, як кажуть, розходиться.
- Нехай\(f(x)\) буде безперервним над\((−∞,+∞)\). Потім\[\int ^{+∞}_{−∞}f(x)\,dx=\int ^0_{−∞}f(x)\,dx+\int ^{+∞}_0f(x)\,dx, \label{improper3} \] за умови, що\(\displaystyle \int ^0_{−∞}f(x)\,dx\) і\(\displaystyle \int ^{+∞}_0f(x)\,dx\) обидва сходяться. Якщо будь-який з цих двох інтегралів розходиться, то\(\displaystyle \int ^{+∞}_{−∞}f(x)\,dx\) розходиться. (Можна показати, що, по суті,\(\displaystyle \int ^{+∞}_{−∞}f(x)\,dx=\int ^a_{−∞}f(x)\,dx+\int ^{+∞}_af(x)\,dx\) для будь-якого значення а.).
У нашому першому прикладі ми повертаємося до питання, яке ми поставили на початку цього розділу: чи є область між графіком\(f(x)=\frac{1}{x}\) і\(x\) -віссю над інтервалом\([1,+∞)\) скінченна або нескінченна?
Визначте, чи є площа між графіком\(f(x)=\dfrac{1}{x}\) і\(x\) -віссю над інтервалом\([1,+∞)\) скінченною або нескінченною.
Рішення
Спочатку робимо швидкий ескіз відповідної області, як показано на малюнку\(\PageIndex{2}\).
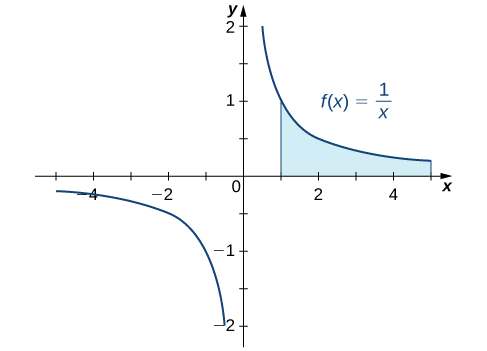
Ми бачимо, що площа цього регіону дається
\[A=\int ^∞_1\frac{1}{x}\,dx. \nonumber \]
які можна оцінити за допомогою рівняння\ ref {improper1}:
\[ \begin{align*} A =\int ^∞_1\frac{1}{x}\,dx \nonumber \\[4pt] =\lim_{t→+∞}\int ^t_1\frac{1}{x}\,dx \tag{Rewrite the improper integral as a limit} \\[4pt] =\lim_{t→+∞}\ln |x|∣^t_1 \tag{Find the antiderivative} \\[4pt] =\lim_{t→+∞}(\ln |t|−\ln 1) \tag{Evaluate the antiderivative} \\[4pt] =+∞. \tag{Evaluate the limit.} \end{align*} \]
Так як неправильний інтеграл\(+∞,\) розходиться до площі області нескінченно.
Знайти об'єм твердого тіла, отриманого обертанням області, обмеженої графіком\(f(x)=\dfrac{1}{x}\) і\(x\) -віссю через інтервал\([1,+∞)\) навколо\(x\) -осі.
Рішення
Тверде тіло показано на рис\(\PageIndex{3}\). Використовуючи дисковий метод, бачимо, що\(V\) том
\[V=π\int ^{+∞}_1\frac{1}{x^2}\,dx. \nonumber \]
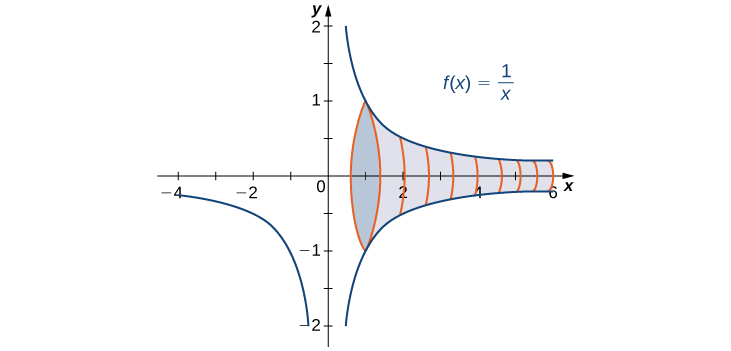
Тоді у нас є
\ [\ стиль відображення\ почати {вирівнювати*} V &= π\ int ^ {+∞} _1\ розрив {1} {x^2}\, dx\\ [4pt]
&= π\ lim_ {t→+∞}\ int ^t_1\ frac {1} {x^2}\, dx\ quad\ текст {Перезаписати як обмеження.}\\ [4pt]
&=π\ lim_ {t→+∞} −\ frac {1} {x} ^t_1\ quad\ text {Знайти антидериватив.}\\ [4pt]
&= π\ lim_ {t→+∞}\ ліворуч (− \ frac {1} {t} +1\ право)\ quad\ text {Оцінити антидериватив.}\\ [4pt]
&=π\ end {align*}\]
Неправильний інтеграл сходиться до\(π\). Тому обсяг твердого тіла обертання є\(π\).
На закінчення, хоча площа області між\(x\) -віссю та графіком\(f(x)=1/x\) над інтервалом\([1,+∞)\) нескінченна, обсяг твердого тіла, що генерується обертанням цієї області навколо\(x\) -осі, є кінцевим. Тверде тіло, що генерується, відомий як Ріг Гавриїла.
Примітка: ріг Габріеля (також називається трубою Торрічеллі) - це геометрична фігура, яка має нескінченну площу поверхні, але кінцевий об'єм. Назва посилається на традицію ідентифікувати архангела Гавриїла як ангела, який дме ріг, щоб оголосити Судний день, асоціюючи божественне або нескінченне, з кінцевим. Властивості цієї фігури вперше вивчила італійський фізик і математик Євангеліста Торрічеллі в 17 столітті.
Припустимо, що на жвавому перехресті дорожньо-транспортні пригоди відбуваються в середньому один раз на три місяці. Після того, як жителі поскаржилися, були внесені зміни в світлофори на перехресті. Минуло вісім місяців з моменту внесення змін, і нещасних випадків не було. Чи були зміни ефективними чи 8-місячний інтервал без випадковості - результат випадковості?

Теорія ймовірностей говорить нам, що якщо середній час між подіями є\(k\)\(X\), ймовірність того, що час між подіями знаходиться між\(a\) і\(b\) задається
\[(P(a≤x≤b)=\int ^b_af(x)\,dx \nonumber \]
де
\[f(x)=\begin{cases}0, \text{if}\;x<0\\ke^{−kx}, \text{if}\;x≥0\end{cases}. \nonumber \]
Таким чином, якщо нещасні випадки відбуваються зі швидкістю один раз в 3 місяці, то ймовірність того\(X\), що час між аваріями\(b\) знаходиться між\(a\) і дається
\[P(a≤x≤b)=\int ^b_af(x)\,dx \nonumber \]
де\[f(x)=\begin{cases}0, \text{if}\;x<0\\3e^{−3x}, \text{if}\;x≥0\end{cases}. \nonumber \]
Щоб відповісти на питання, ми повинні обчислити\(\displaystyle P(X≥8)=\int ^{+∞}_83e^{−3x}\,dx\) і вирішити, чи ймовірно, що 8 місяців могли б пройти без аварії, якби не було поліпшення дорожньої ситуації.
Рішення
Нам потрібно обчислити ймовірність як неправильний інтеграл:
\ (\ стиль відображення\ почати {вирівнювати*} P (X≥8) =\ int ^ {+∞} _83e^ {−3x}\, дх\\ [4pt]
=\ lim_ {t→+∞}\ int ^t_83e^ {−3x}\, dx\\ [4pt]
=\ lim_ {t→+∞} −e^ {−3x} ^t_8\\ [4pt]
=\ lim_ {t→+∞} (−e^ {−3t} +e^ {−24})\\ [4pt]
≈3,8×10^ {−11}. \ end {вирівнювати*}\)
Значення\(3.8×10^{−11}\) представляє ймовірність відсутності нещасних випадків за 8 місяців при початкових умовах. Оскільки ця величина дуже і дуже мала, то розумно зробити висновок, що зміни виявилися ефективними.
Оцініть\(\displaystyle \int ^0_{−∞}\frac{1}{x^2+4}\,dx.\) стан, чи збігається неправильний інтеграл або розходиться.
Рішення
Почніть з перезапису\(\displaystyle \int ^0_{−∞}\frac{1}{x^2+4}\,dx\) як обмеження за допомогою Equation\ ref {improper2} з визначення. Таким чином,
\ [\ begin {align*}\ int ^0_ {−∞}\ розрив {1} {x^2+4}\, dx &=\ lim_ {t→−∞}\ int ^0_t\ frac {1} {x^2+4}\, dx\ quad\ text {Перезаписати як межу.}\\ [4pt]
&=\ lim_ {t→∞} розрив {1} {2}\ tan^ {−1}\ frac {x} {2} ^0_t\ quad\ text {Знайти антипохідну.}\\ [4pt]
&=\ lim_ {t→−∞}\ ліворуч (\ frac {1} {2}\ tan^ {−1} 0−\ frac {1} {2}\ tan^ {−1}\ frac {t} {2}\ право)\ quad\ text {Оцінити антидериватив.}\\ [4pt]
&=\ frac {π} {4}. \ quad\ text {Оцінити ліміт і спростити.} \ end {вирівнювати*}\]
Неправильний інтеграл сходиться до\(\dfrac{π}{4}.\)
Оцініть\(\displaystyle \int ^{+∞}_{−∞}xe^x\,dx.\) стан, чи збігається неправильний інтеграл або розходиться.
Рішення
Почніть з поділу інтеграла:
\[\int ^{+∞}_{−∞}xe^x\,dx=\int ^0_{−∞}xe^x\,dx+\int ^{+∞}_0xe^x\,dx. \nonumber \]
Якщо або\(\displaystyle \int ^0_{−∞}xe^x\,dx\) або\(\displaystyle \int ^{+∞}_0xe^x\,dx\) розходиться, то\(\displaystyle \int ^{+∞}_{−∞}xe^x\,dx\) розходиться. Обчислити кожен інтеграл окремо. Для першого інтеграла,
\(\displaystyle \int ^0_{−∞}xe^x\,dx=\lim_{t→−∞}\int ^0_txe^x\,dx\)Перепишіть як ліміт.
\(=\lim_{t→−∞}(xe^x−e^x)∣^0_t\)Використовуйте інтеграцію по частинам, щоб знайти антидериватив. (Тут\(u=x\) і\(dv=e^x\).)
\(=\lim_{t→−∞}(−1−te^t+e^t)\)Оцініть антидериватив.
\(=−1.\)
Оцініть ліміт. Примітка:\(\displaystyle \lim_{t→−∞}te^t\) є невизначеною формою.\(0⋅∞\) Таким чином,\(\displaystyle \lim_{t→−∞}te^t=\lim_{t→−∞}\frac{t}{e^{−t}}=\lim_{t→−∞}\frac{−1}{e^{−t}}=\lim_{t→−∞}−e^t=0\) за правилом L'Hôpital.
Перший неправильний інтеграл сходиться. Для другого інтеграла,
\(\displaystyle \int ^{+∞}_0xe^x\,dx=\lim_{t→+∞}\int ^t_0xe^x\,dx\)Перепишіть як ліміт.
\(=\lim_{t→+∞}(xe^x−e^x)∣^t_0\)Знайдіть антидериватив.
\(=\lim_{t→+∞}(te^t−e^t+1)\)Оцініть антидериватив.
\(=\lim_{t→+∞}((t−1)e^t+1)\)Перепишіть. (\(te^t−e^t\)є невизначеною.)
\(=+∞.\)Оцініть ліміт.
Таким чином,\(\displaystyle \int ^{+∞}_0xe^x\,dx\) розходиться. Оскільки цей інтеграл\(\displaystyle \int ^{+∞}_{−∞}xe^x\,dx\) розходиться, розходиться також.
Оцініть\(\displaystyle \int ^{+∞}_{−3}e^{−x}\,dx.\) стан, чи збігається неправильний інтеграл або розходиться.
- Підказка
-
\[\int ^{+∞}_{−3}e^{−x}\,dx=\lim_{t→+∞}\int ^t_{−3}e^{−x}\,dx \nonumber \]
- Відповідь
-
Він сходиться до\(e^3.\)
Інтеграція розривного інтегралу
Тепер розглянемо інтеграли функцій, що містять нескінченний розрив в інтервалі, через який відбувається інтеграція. Розглянемо інтеграл форми,\(\displaystyle \int ^b_af(x)\,dx,\) де\(f(x)\) є безперервним над\([a,b)\) і переривчастим в\(b\). Оскільки функція\(f(x)\) є безперервною\([a,t]\) для всіх значень\(t\) задовольняє\(a \le t<b\), інтеграл\(\displaystyle \int ^t_af(x)\,dx\) визначається для всіх таких значень\(t\). Таким чином, має сенс розглядати цінності\(\displaystyle \int ^t_af(x)\,dx\) як\(t\) підходи\(b\) для\(a \le t<b\). Тобто ми визначаємо, за умови\(\displaystyle \int ^b_af(x)\,dx=\lim_{t→b^−}\int ^t_af(x)\,dx\), що цей ліміт існує. Малюнок\(\PageIndex{5}\) ілюструє\(\displaystyle \int ^t_af(x)\,dx\) як області регіонів для значень\(t\) наближення\(b\).
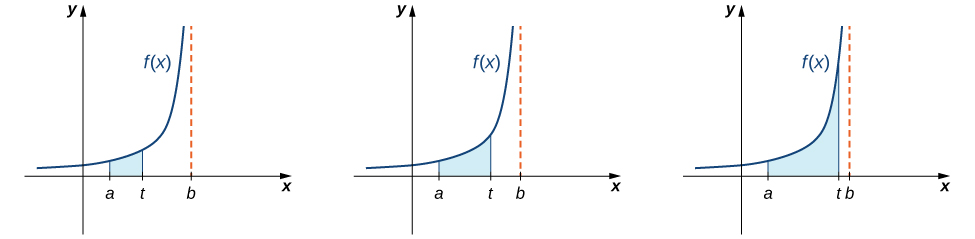
Ми використовуємо подібний підхід для визначення\(\displaystyle \int ^b_af(x)\,dx\), де\(f(x)\) знаходиться безперервне над\((a,b]\) і переривчастим в\(a\). Тепер приступимо до формального визначення.
- Нехай\(f(x)\) буде безперервним над\([a,b)\). Потім,\[\int ^b_af(x)\,dx=\lim_{t→b^−}\int ^t_af(x)\,dx. \label{improperundefb} \]
- Нехай\(f(x)\) буде безперервним над\((a,b]\). Потім,\[\int ^b_af(x)\,dx=\lim_{t→a^+}\int ^b_tf(x)\,dx. \label{improperundefa} \] У кожному випадку, якщо межа існує, то неправильний інтеграл, як кажуть, сходяться. Якщо межі не існує, то неправильний інтеграл, як кажуть, розходиться.
- Якщо\(f(x)\) безперервно над\([a,b]\) хіба що в точці\(c\) в\((a,b)\), то за\[\int ^b_af(x)\,dx=\int ^c_af(x)\,dx+\int ^b_cf(x)\,dx,\label{improperundefc} \] умови обох\(\displaystyle \int ^c_af(x)\,dx\) і\(\displaystyle \int ^b_cf(x)\,dx\) сходяться. Якщо будь-який з цих інтегралів розходиться, то\(\displaystyle \int ^b_af(x)\,dx\) розходиться.
Наступні приклади демонструють застосування даного визначення.
Оцініть\(\displaystyle \int ^4_0\frac{1}{\sqrt{4−x}}\,dx,\), якщо це можливо. Створіть, чи збігається інтеграл або розходиться.
Рішення
Функція\(f(x)=\dfrac{1}{\sqrt{4−x}}\) є безперервною\([0,4)\) і переривчастою при 4. Використовуючи Equation\ ref {improperundefb} з визначення, перепишіть\(\displaystyle \int ^4_0\frac{1}{\sqrt{4−x}}\,dx\) як ліміт:
\ (\ displaystyle\ begin {align*}\ int ^4_0\ frac {1} {\ sqrt {4−x}}\, dx &=\ lim_ {t→4^−}\ int ^t_0\ frac {1} {\ sqrt {4−x}}\, dx\ quad\ text {Переписати як обмеження.}\\ [4pt]
&=\ lim_ {t→4^−} (−2\ sqrt {4−x}) ^t_0\ quad\ text {Знайти антипохідну.}\\ [4pt]
&=\ lim_ {t→4^−} (−2\ sqrt {4−t} +4)\ quad\ text {Оцінити антидериватив.}\\ [4pt]
&=4. \ quad\ text {Оцінити ліміт.} \ end {вирівнювати*}\)
Неправильний інтеграл сходиться.
Оцініть\(\displaystyle \int ^2_0x\ln x\,dx.\) стан, чи збігається інтеграл або розходиться.
Рішення
Оскільки\(f(x)=x\ln x\) є безперервним\((0,2]\) і є переривчастим на нулі, ми можемо переписати інтеграл у граничній формі за допомогою Equation\ ref {improperundefa}:
\ (\ стиль відображення\ почати {align*}\ int ^2_0x\ ln x\ ln x\, dx &=\ lim_ {t→0^+}\ int ^2_tx\ ln x\ ln x\, dx\ quad\ text {Перепишіть як межу.}\\ [4pt]
&=\ lim_ {t→0^+} (\ frac {1} {2} x^2\ ln x -\ frac {1} {4} x^2) ^2_t\ quad\ text {Оцінювати}\;\ int x\ ln x\, dx\;\ text {використовуючи інтеграцію частинами з}\; u=\ ln x\;\ text {і}\; dv=x. \\ [4pt]
&=\ lim_ {t→0^+} (2\ ln 2−1−\ frac {1} {2} t^2\ ln t+\ frac {1} {4} t^2). \ quad\ text {Оцінити антидериватив.}\\ [4pt]
&=2\ ln 2−1. \ quad\ text {Оцінити ліміт.} \ end {вирівнювати*}\)
Тому
\(\displaystyle \lim_{t→0^+}t^2\ln t\;\text{is indeterminate.}\)
Щоб оцінити його, перепишіть як частку і застосуйте правило L'Hôpital.
Неправильний інтеграл сходиться.
Оцініть\(\displaystyle \int ^1_{−1}\frac{1}{x^3}\,dx.\) стан, чи збігається неправильний інтеграл або розходиться.
Рішення
Оскільки\(f(x)=1/x^3\) є переривчастим на нулі, використовуючи Equation\ ref {improperundefc}, ми можемо записати
\[\int ^1_{−1}\frac{1}{x^3}\,dx=\int ^0_{−1}\frac{1}{x^3}\,dx+\int ^1_0\frac{1}{x^3}\,dx.\nonumber \]
Якщо будь-який з двох інтегралів розходиться, то вихідний інтеграл розходиться. Почніть з\(\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx\):
\(\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx=\lim_{t→0^−}\int ^t_{−1}\frac{1}{x^3}\,dx\)Перепишіть як ліміт.
\(=\lim_{t→0^−}(−\frac{1}{2x^2})∣^t_{−1}\)Знайдіть антидериватив.
\(=\lim_{t→0^−}(−\frac{1}{2t^2}+\frac{1}{2})\)Оцініть антидериватив.
\(=+∞.\)Оцініть ліміт.
Тому\(\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx\) розходиться. Так як\(\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx\) розходиться,\(\displaystyle \int ^1_{−1}\frac{1}{x^3}\,dx\) розходиться.
Оцініть\(\displaystyle \int ^2_0\frac{1}{x}\,dx.\) стан, чи збігається інтеграл або розходиться.
- Підказка
-
Запишіть\(\displaystyle \int ^2_0\frac{1}{x}\,dx\) в граничній формі за допомогою Рівняння\ ref {improperundefa}.
- Відповідь
-
\(+∞\), Це розходиться.
Теорема порівняння
Не завжди легко або навіть можливо оцінити неправильний інтеграл безпосередньо; однак, порівнюючи його з іншим ретельно підібраним інтегралом, можна визначити його збіжність або розбіжність. Щоб переконатися в цьому, розглянемо дві неперервні функції\(f(x)\) і\(g(x)\) задовольняють\(0≤f(x)≤g(x)\) для\(x≥a\) (рис.\(\PageIndex{6}\)). У цьому випадку ми можемо розглядати інтеграли цих функцій через інтервали форми\([a,t]\) як області, тому ми маємо зв'язок
\[ 0≤\int ^t_af(x)\,dx≤\int ^t_ag(x)\,dx \nonumber \]
для\(t≥a\).
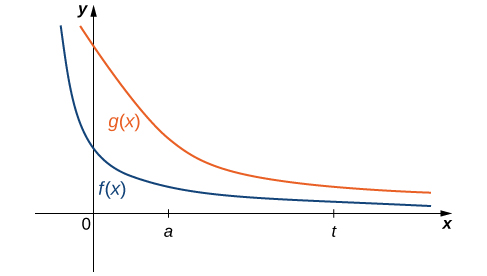
Таким чином, якщо
\[\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=+∞, \nonumber \]
потім
\[\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=+∞ \nonumber \]
а також. Тобто, якщо площа області між графіком\(f(x)\) і\(x\) -віссю над\([a,+∞)\) нескінченною, то площа області між графіком\(g(x)\) і\(x\) -віссю над теж\([a,+∞)\) нескінченна.
З іншого боку, якщо
\[\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=L \nonumber \]
для деякого реального числа\(L\), то
\[\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx \nonumber \]
повинні сходитися до деякого значення менше або дорівнює\(L\), оскільки\(\displaystyle \int ^t_af(x)\,dx\)\(t\) збільшується зі збільшенням і\(\displaystyle \int ^t_af(x)\,dx≤L\) для всіх\(t≥a.\)
Якщо площа області між графіком\(g(x)\) і\(x\) -віссю над\([a,+∞)\) кінцевою, то площа області між графіком\(f(x)\) і\(x\) -віссю над також\([a,+∞)\) кінцева.
Ці висновки узагальнені в наступній теоремі.
\(g(x)\)Дозволяти\(f(x)\) і бути безперервним над\([a,+∞).\) Припустимо, що\(0≤f(x)≤g(x)\) для\(x≥a.\)
- Якщо\[\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=+∞, \nonumber \] тоді\[\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=+∞. \nonumber \]
- Якщо\[\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=L, \nonumber \] де\(L\) дійсне число, то\[\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=M \nonumber \] для деякого дійсного числа\(M≤L.\)
Використовуйте порівняння, щоб показати, що
\[\int ^{+∞}_1\frac{1}{xe^x}\,dx \nonumber \]
сходиться.
Рішення
Ми бачимо, що
\[0≤\frac{1}{xe^x}≤\frac{1}{e^x}=e^{−x}, \nonumber \]
так що якщо\(\displaystyle \int ^{+∞}_1e^{−x}\,dx\) сходиться, то так і відбувається\(\displaystyle \int ^{+∞}_1\frac{1}{xe^x}\,dx\). Щоб оцінити\(\displaystyle \int ^{+∞}_1e^{−x}\,dx,\) спочатку перепишіть його як ліміт:
\(\displaystyle \int ^{+∞}_1e^{−x}\,dx=\lim_{t→+∞}\int ^t_1e^{−x}\,dx\)
\(=\lim_{t→+∞}(−e^{−x})∣^t_1\)
\(=\lim_{t→+∞}(−e^{−t}+e^{-1})\)
\(=e^{-1}.\)
Так як\(\displaystyle \int ^{+∞}_1e^{−x}\,dx\) сходиться, так і робить\(\displaystyle \int ^{+∞}_1\frac{1}{xe^x}\,dx.\)
Використовуйте теорему порівняння, щоб показати, що\(\displaystyle \int ^{+∞}_1\frac{1}{x^p}\,dx\) розходиться для всіх\(p<1\).
Рішення
\([1,+∞).\)На\(p<1, 1/x≤1/(x^p)\) прикладі ми показали\(\PageIndex{1}\), що\(\displaystyle \int ^{+∞}_1\frac{1}{x}\,dx=+∞.\) Тому\(\displaystyle \int ^{+∞}_1\frac{1}{x^p}\,dx\) розходиться для всіх\(p<1\).
Використовуйте порівняння, щоб показати, що\(\displaystyle \int ^{+∞}_e\frac{\ln x}{x}\,dx\) розходиться.
- Підказка
-
\(\frac{1}{x}≤\frac{\ln x}{x}\)на\([e,+∞)\)
- Відповідь
-
Так як\(\displaystyle \int ^{+∞}_e\frac{1}{x}\,dx=+∞,\)\(\displaystyle \int ^{+∞}_e\frac{\ln x}{x}\,dx\) розходиться.
В останніх кількох розділах ми розглянули кілька способів використання інтеграції для вирішення реальних проблем. Для цього наступного проекту ми будемо досліджувати більш досконале застосування інтеграції: інтегральні перетворення. Зокрема, ми опишемо перетворення Лапласа та деякі його властивості. Перетворення Лапласа використовується в техніці та фізиці для спрощення обчислень, необхідних для вирішення деяких завдань. Він приймає функції, виражені через час, і перетворює їх у функції, виражені через частоту. Виявляється, що в багатьох випадках обчислення, необхідні для вирішення проблем у частотній області, набагато простіші, ніж ті, які потрібні в часовій області.
Перетворення Лапласа визначається термінами інтеграла як
\[L{f(t)}=F(s)=\int ^∞_0e^{−st}f(t)dt. \nonumber \]
Зверніть увагу, що вхід для перетворення Лапласа є функцією часу,\(f(t),\) а вихід - функція частоти,\(F(s)\). Хоча багато реальних прикладів вимагають використання комплексних чисел (залучаючи уявне число\(i=\sqrt{−1}),\) в цьому проекті, ми обмежуємося функціями дійсних чисел.
Почнемо з простого прикладу. Тут ми обчислюємо перетворення Лапласа\(f(t)=t\). У нас є
\[L{t}=\int ^∞_0te^{−st}dt. \nonumber \]
Це неправильний інтеграл, тому ми виражаємо його з точки зору ліміту, який дає
\[L{t}=\int ^∞_0te^{−st}dt=\lim_{z→∞}\int ^z_0te^{−st}dt. \nonumber \]
Тепер ми використовуємо інтеграцію по частинам, щоб оцінити інтеграл. Зауважте, що ми інтегруємо щодо t, тому ми розглядаємо змінну s як константу. У нас є
\(u=t\)\(du=dt\)\(dv=e^{−st}dt\)\(v=−\frac{1}{s}e^{−st}\).
Тоді отримуємо
\[ \begin{align*} \lim_{z→∞}\int ^z_0te^{−st}dt =\lim_{z→∞}[[−\frac{t}{s}e^{−st}]∣^z_0+\frac{1}{s}\int ^z_0e^{−st}dt] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}+\frac{0}{s}e^{−0s}]+\frac{1}{s}\int ^z_0e^{−st}dt] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}+0]−\frac{1}{s}[\frac{e^{−st}}{s}]∣^z_0] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}]−\frac{1}{s^2}[e^{−sz}−1]] \\[4pt]\ =\lim_{z→∞}[−\frac{z}{se^{sz}}]−\lim_{z→∞}[\frac{1}{s^2e^{sz}}]+\lim_{z→∞}\frac{1}{s^2} \\[4pt]\ =0−0+\frac{1}{s^2} \\[4pt]\ =\frac{1}{s^2}. \end{align*}\]
- Обчисліть перетворення Лапласа\(f(t)=1.\)
- Обчисліть перетворення Лапласа\(f(t)=e^{−3t}.\)
- Обчисліть перетворення Лапласа\(f(t)=t^2\). (Зверніть увагу, вам доведеться інтегрувати по частинам двічі.)
Перетворення Лапласа часто використовуються для розв'язання диференціальних рівнянь. Диференціальні рівняння не розглядаються докладно пізніше в цій книзі; але поки давайте розглянемо зв'язок між перетворенням Лапласа функції та перетворенням Лапласа її похідної.
Почнемо з визначення перетворення Лапласа. У нас є
\[L{f(t)}=\int ^∞_0e^{−st}f(t)dt=\lim_{z→∞}\int ^z_0e^{−st}f(t)dt. \nonumber \]
Використовуйте інтеграцію по частинам для оцінки\(\displaystyle \lim_{z→∞}\int ^z_0e^{−st}f(t)dt\). (Нехай\(u=f(t)\) і\(dv=e^{−st}dt\).)
Після інтеграції частинами та оцінки ліміту ви повинні побачити, що
\[L{f(t)}=\frac{f(0)}{s}+\frac{1}{s}[L{f′(t)}]. \nonumber \]
Потім,
\[L{f′(t)}=sL{f(t)}−f(0). \nonumber \]
Таким чином, диференціація в часовій області спрощує множення на s в частотній області.
Останнє, на що ми дивимося в цьому проекті, - це те, як Лаплас перетворюється\(f(t)\) та його антипохідні пов'язані між собою. Нехай\(g(t)=\int ^t_0f(u)du.\) тоді,
\[L{g(t)}=\int ^∞_0e^{−st}g(t)dt=\lim_{z→∞}\int ^z_0e^{−st}g(t)dt. \nonumber \]
Використовуйте інтеграцію по частинам для оцінки\(\displaystyle \lim_{z→∞}\int ^z_0e^{−st}g(t)dt.\) (Дозвольте\(u=g(t)\) і\(dv=e^{−st}dt\). Зверніть увагу, до речі, що ми визначили\(g(t), du=f(t)dt.\))
Як і слід було очікувати, ви повинні побачити, що
\[L{g(t)}=\frac{1}{s}⋅L{f(t)}. \nonumber \]
Інтеграція в часовій області спрощує поділ\(s\) на частотну область.
Ключові концепції
- Інтеграли функцій через нескінченні інтервали визначено через межі.
- Інтеграли функцій за інтервал, для якого функція має розрив у кінцевій точці, можуть бути визначені через межі.
- Збіжність або розбіжність неправильного інтеграла може бути визначена шляхом порівняння його зі значенням неправильного інтеграла, для якого відома збіжність або розбіжність.
Ключові рівняння
- неправильні інтеграли
\(\displaystyle \int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx\)
\(\displaystyle \int ^b_{−∞}f(x)\,dx=\lim_{t→−∞}\int ^b_tf(x)\,dx\)
\(\displaystyle \int ^{+∞}_{−∞}f(x)\,dx=\int ^0_{−∞}f(x)\,dx+\int ^{+∞}_0f(x)\,dx\)
Глосарій
- неправильний інтеграл
- інтеграл через нескінченний інтервал або інтеграл функції, що містить нескінченний розрив на інтервалі; неправильний інтеграл визначається через межу. Неправильний інтеграл сходиться, якщо ця межа є скінченним дійсним числом; в іншому випадку неправильний інтеграл розходиться
