5.1: Апроксимаційні області

Last updated
Save as PDF

Page ID: 61776

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Використовуйте сигматичні (підсумовані) позначення для обчислення сум і степенів цілих чисел.
Використовуйте суму прямокутних площ, щоб наблизити площу під кривою.
Використовуйте суми Рімана для наближення площі.

Архімед був захоплений обчисленням площ різних форм - іншими словами, кількості простору, обкладеного формою. Він використовував процес, який став відомим як метод виснаження, який використовував менші та менші форми, площі яких можна було точно розрахувати, щоб заповнити нерегулярну область і тим самим отримати ближче і ближче наближення до загальної площі. У цьому процесі область, обмежена кривими, заповнюється прямокутниками, трикутниками та формами з точними формулами площі. Потім ці області підсумовуються, щоб наблизити площу криволінійної області.

У цьому розділі ми розробляємо методи наближення площі між кривою, визначеною функцією$f(x),$ і віссю x на замкнутому інтервалі$[a,b].$ Як і Архімед, ми спочатку наближаємо площу під кривою, використовуючи форми відомої області (а саме прямокутники). Використовуючи менші та менші прямокутники, ми отримуємо все ближче і ближче наближення до площі. Прийняття ліміту дозволяє обчислити точну площу під кривою.

Почнемо з введення деяких позначень, щоб полегшити обчислення. Потім ми розглянемо випадок, коли$f(x)$ є безперервним і ненегативним. Пізніше в розділі ми послаблюємо деякі з цих обмежень і розробляємо методи, які застосовуються в більш загальних випадках.

Сигма (підсумовування) позначення

Як уже згадувалося, ми будемо використовувати форми відомої області для наближення площі нерегулярної області, обмеженої кривими. Цей процес часто вимагає складання довгих рядків чисел. Щоб полегшити запис цих довгих сум, ми розглянемо деякі нові позначення тут, які називаються сигма-нотацією (також відомі як підсумовування). Грецька велика буква$Σ$, сигма, використовується для вираження довгих сум значень в компактній формі. Наприклад, якщо ми хочемо додати всі цілі числа від 1 до 20 без сигма-нотації, ми повинні написати

\[1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20. \nonumber \]

Ми могли б, ймовірно, пропустити написання пари термінів і написати

\[1+2+3+4+⋯+19+20, \nonumber \]

який краще, але все ж громіздкий. З сигма-позначенням запишемо цю суму як

\[\sum_{i=1}^{20}i \nonumber \]

який набагато компактніше. Як правило, сигма-позначення представлені у вигляді

\[\sum_{i=1}^{n}a_i \nonumber \]

де$a_i$ описуються терміни, які потрібно додати, а$i$ називається$index$. Кожен член оцінюється, потім ми підсумовуємо всі значення, починаючи зі значення коли$i=1$ і закінчуючи значенням коли$i=n.$ Наприклад, вираз$\displaystyle \sum_{i=2}^{7}s_i$ подібне інтерпретується як$s_2+s_3+s_4+s_5+s_6+s_7$. Зверніть увагу, що індекс використовується лише для відстеження умов, які потрібно додати; він не враховує при розрахунку самої суми. Тому індекс називається фіктивною змінною. Ми можемо використовувати будь-яку букву, яка нам подобається для індексу. Як правило, математики використовують$i, \,j, \,k, \,m$ і$n$ для індексів.

Спробуємо пару прикладів використання сигма-позначень.

Приклад$\PageIndex{1}$: Using Sigma Notation

Напишіть сигма-позначення і оцініть суму термінів$3^i$ для$i=1,2,3,4,5.$
Запишіть суму в сигма-позначеннях:

\[1+\dfrac{1}{4}+\dfrac{1}{9}+\dfrac{1}{16}+\dfrac{1}{25}. \nonumber \]

Рішення

Напишіть\[\sum_{i=1}^{5}3^i=3+3^2+3^3+3^4+3^5=363. \nonumber \]
Знаменник кожного члена - ідеальний квадрат. Використовуючи сигма-позначення, цю суму можна записати як$\displaystyle \sum_{i=1}^5\dfrac{1}{i^2}$.

Вправа$\PageIndex{1}$

Напишіть сигма-позначення і оцініть суму термінів$2^i$ для$i=3,4,5,6.$

Підказка: Скористайтеся кроками розв'язання в прикладі$\PageIndex{1}$ як орієнтиром.

Відповідь: $\displaystyle \sum_{i=3}^{6}2^i=2^3+2^4+2^5+2^6=120$

Властивості, пов'язані з процесом підсумовування, наведені в наступному правилі.

Правило: Властивості сигма-позначення

$b_1,b_2,…,b_n$Дозволяти$a_1,a_2,…,a_n$ і представляють дві послідовності термінів і нехай$c$ бути константою. Наступні властивості утримуються для всіх натуральних чисел$n$ і для цілих чисел$m$, з$1≤m≤n.$

$\displaystyle \sum_{i=1}^n c=nc$
$\displaystyle \sum_{i=1}^n ca_i=c\sum_{i=1}^na_i$
$\displaystyle \sum_{i=1}^n(a_i+b_i)=\sum_{i=1}^na_i+\sum_{i=1}^nb_i$
$\displaystyle \sum_{i=1}^n(a_i−b_i)=\sum_{i=1}^na_i−\sum_{i=1}^nb_i$
$\displaystyle \sum_{i=1}^na_i=\sum_{i=1}^ma_i+\sum_{i=m+1}^na_i$

Доказ

Доводимо властивості (ii.) і (iii.) тут, і залишаємо докази інших властивостей у Вправи.

(II.) У нас є

\[\sum_{i=1}^nca_i=ca_1+ca_2+ca_3+⋯+ca_n=c(a_1+a_2+a_3+⋯+a_n)=c\sum_{i=1}^na_i. \nonumber \]

(ііі.) У нас є

\[ \begin{align} \sum_{i=1}^{n}(a_i+b_i) &=(a_1+b_1)+(a_2+b_2)+(a_3+b_3)+⋯+(a_n+b_n) \\[4pt] &=(a_1+a_2+a_3+⋯+a_n)+(b_1+b_2+b_3+⋯+b_n) \\[4pt] &=\sum_{i=1}^na_i+\sum_{i=1}^nb_i. \end {align} \nonumber \]

□

Ще кілька формул для часто зустрічаються функцій спрощують процес підсумовування далі. Вони показані в наступному правилі, для сум і степенів цілих чисел, і ми використовуємо їх у наступному наборі прикладів.

Правило: Суми та степені цілих чисел

1. Сума$n$ цілих чисел задається

\[\sum_{i=1}^n i=1+2+⋯+n=\dfrac{n(n+1)}{2}. \label{sum1} \]

2. Сума послідовних цілих чисел у квадраті задається

\[\sum_{i=1}^n i^2=1^2+2^2+⋯+n^2=\dfrac{n(n+1)(2n+1)}{6}. \label{sum2} \]

3. Суму послідовних цілих чисел в кубі задано

\[\sum_{i=1}^n i^3=1^3+2^3+⋯+n^3=\dfrac{n^2(n+1)^2}{4}. \label{sum3} \]

Приклад$\PageIndex{2}$: Evaluation Using Sigma Notation

Напишіть за допомогою сигма-нотації і оцініть:

Сума термінів$(i−3)^2$ за$i=1,2,…,200.$
Сума термінів$(i^3−i^2)$ за$i=1,2,3,4,5,6$

Рішення

a. множивши$(i−3)^2$, ми можемо розбити вираз на три члени.

\ [\ почати {вирівнювати*}\ сума_ {i = 1} ^ {200} (i−3) ^2 &=\ сума_ {i = 1} ^ {200} (i^2−6i+9)\\ [4pt]
&=\ сума {i = 1} ^ {200} i^2−\ сума {i = 1} ^ {200} 6i+\ sum_ {i=1} ^ {200} 9\\ [4pt]
&=\ сума {i=1} ^ {200} i^2−6\ сума {i=1} ^ {200} i+\ sum_ {i=1} ^ {200} 9\\ [4pt]
&=\ dfrac {200 (200+1) (400+1)}} {6} −6\ ліворуч [ dfrac {200 (200+1)} {2}\ праворуч] +9 (200)\\ [4pt]
&=2,686,700−120,600+1800\\ [4pt]
&= 2,567,900\ кінець {вирівнювати*}\]

б. використовувати властивість сигма-позначення iv. і правила для суми квадратних термінів і суми кубічних термінів.

\ [\ почати {вирівнювати*}\ сума_ {i = 1} ^ {6} (i^3−i^2) &=\ сума_ {i=1} ^6 i^3−\ sum_ {i=1} ^6 i ^ 2\\ [4pt]
&=\ dfrac {6^2 (6+1) ^2} {4} −\ dfrac {6 (6+1) ^2} {4} −\ dfrac {6 (6+1)) (2 (6) +1)} {6}\\ [4pt]
&=\ dfrac {1764} {4} −\ dfrac {546} {6}\\ [4pt]
&= 350\ кінець {вирівнювати*}\ nonumber\]

Вправа$\PageIndex{2}$

Знайти суму значень$4+3i$ for$i=1,2,…,100.$

Підказка: Використовуйте властивості сигма-позначення для вирішення проблеми.

Відповідь: $15,550$

Приклад$\PageIndex{3}$: Finding the Sum of the Function Values

Знайти суму значень$f(x)=x^3$ над цілими числами$1,2,3,…,10.$

Рішення

Використовуючи рівняння\ ref {sum3}, ми маємо

\[\sum_{i=0}^{10}i^3=\dfrac{(10)^2(10+1)^2}{4}=\dfrac{100(121)}{4}=3025 \nonumber \]

Вправа$\PageIndex{3}$

Оцініть суму, зазначену позначенням$\displaystyle \sum_{k=1}^{20}(2k+1)$.

Підказка: Використовуйте правило щодо суми та степенів цілих чисел (Рівняння\ ref {sum1} -\ ref {sum3}).

Відповідь: $440$

Апроксимаційна площа

Тепер, коли у нас є необхідні позначення, ми повертаємося до поставленої задачі: наближення площі під кривою. $f(x)$Дозволяти неперервна, невід'ємна функція, визначена на замкнутому інтервалі$[a,b]$. Ми хочемо наблизити область,$A$ обмежену$f(x)$ вище,$x$ -вісь нижче, лінію$x=a$ зліва та лінію$x=b$ праворуч (рис.$\PageIndex{1}$).

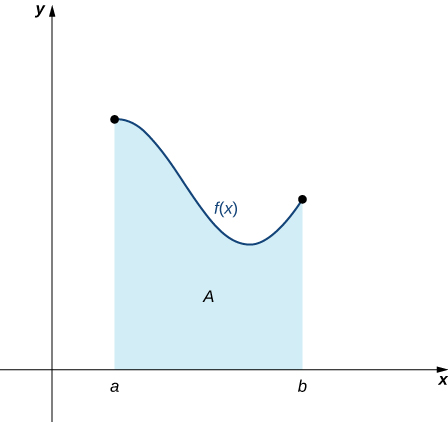
Графік у квадранті — одна з області, обмеженої загальною кривою f (x) вгорі, віссю x внизу, лінією x = a ліворуч та лінією x = b праворуч. Приблизно на середині, увігнутість перемикається від увігнутої вниз до увігнутої вгору, і функція починає збільшуватися незадовго до лінії x = b. — Малюнок$\PageIndex{1}$: Область (затінена область), обмежена кривою$f(x)$ вгорі,$x$ -віссю внизу, лінією$x=a$ ліворуч та$x=b$ лінією праворуч.

Як ми наближаємо площу під цією кривою? Підхід геометричний. Розділивши область на багато малих форм, які мають відомі формули площі, ми можемо підсумувати ці площі та отримати розумну оцінку справжньої площі. Починаємо з поділу інтервалу$[a,b]$ на$n$ підінтервали рівної ширини,$\dfrac{b−a}{n}$. Робимо це, вибираючи однаково розташовані точки$x_0,x_1,x_2,…,x_n$ з$x_0=a,x_n=b,$ і

\[x_i−x_{i−1}=\dfrac{b−a}{n} \nonumber \]

для$i=1,2,3,…,n.$

Позначимо ширину кожного підінтервала позначеннями$Δx,$ так$Δx=\frac{b−a}{n}$ і

\[x_i=x_0+iΔx \nonumber \]

Для$i=1,2,3,…,n.$ цього поняття ділення інтервалу$[a,b]$ на підінтервали шляхом вибору точок зсередини інтервалу використовується досить часто при наближенні площі під кривою, тому давайте визначимо деяку відповідну термінологію.

Визначення: Перегородки

Безліч точок$P={x_i}$ для$i=0,1,2,…,n$ з$a=x_0 < x_1 < x_2 < ... < x_n = b$, яка$[a, b]$ ділить інтервал на підінтервали$[x_0, x_1], [x_1, x_2], ..., [x_{n-1}, x_n]$ виду називається aперегородка$[a,b]$. Якщо всі підінтервали мають однакову ширину, множина точок утворює регулярний розділ (або рівномірний розділ) інтервалу$[a,b].$

Ми можемо використовувати цей регулярний розділ як основу методу оцінки площі під кривою. Далі ми розглянемо два методи: наближення лівої кінцевої точки та наближення правої кінцевої точки.

Правило: Наближення лівої кінцевої точки

На кожному підінтервалі$[x_{i−1},x_i]$ (for$i=1,2,3,…,n$) побудуйте прямокутник з шириною$Δx$ і висотою рівними$f(x_{i−1})$, що є значенням функції в лівій кінцевій точці субінтервалу. Тоді площа цього прямокутника дорівнює$f(x_{i−1})Δx$. Склавши площі всіх цих прямокутників, отримуємо приблизне значення для$A$ (рис.$\PageIndex{2}$). Ми використовуємо позначення,$L_n$ щоб позначити, що це ліва кінцева точка наближення$A$ використання$n$ підінтервалів.

\[A≈L_n=f(x_0)Δx+f(x_1)Δx+⋯+f(x_{n−1})Δx=\sum_{i=1}^nf(x_{i−1})Δx \nonumber \]

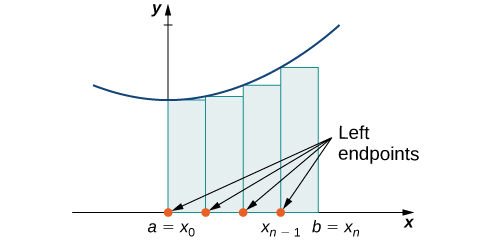
Діаграма, що показує наближення площі під кривою лівою кінцевою точкою. Під параболою з вершиною на осі y і над віссю x прямокутники малюються між a=x0 на початку і b = xn. Прямокутники мають кінцеві точки на a=x0, x1, x2... x (n-1) та b = xn, розташовані однаково. Висота кожного прямокутника визначається значенням заданої функції в лівій кінцевій точці прямокутника. — Рисунок$\PageIndex{2}$: У лівій кінцевій точці наближення площі під кривою висота кожного прямокутника визначається значенням функції зліва від кожного підінтервалу.

Другий метод апроксимації площі під кривою - це наближення правої кінцевої точки. Це майже те ж саме, що і наближення лівої кінцевої точки, але тепер висоти прямокутників визначаються значеннями функцій праворуч від кожного підінтервалу.

Правило: наближення правої кінцевої точки

Побудувати прямокутник на кожному підінтервалі$[x_{i−1},x_i]$, тільки на цей раз висота прямокутника визначається значенням функції$f(x_i)$ в правій кінцевій точці підінтервалу. Потім площа кожного прямокутника дорівнює$f(x_i)\,Δx$ і наближення для$A$ задається

\[A≈R_n=f(x_1)Δx+f(x_2)Δx+⋯+f(x_n)Δx=\sum_{i=1}^nf(x_i)Δx. \nonumber \]

Позначення$R_n$ вказує на те, що це наближення правої кінцевої точки для$A$ (рис.$\PageIndex{3}$).

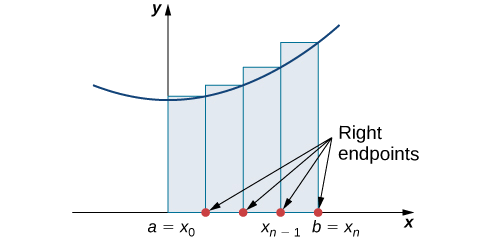
Діаграма, що показує наближення правої кінцевої точки площі під кривою. Під параболою з вершиною на осі y і над віссю x прямокутники малюються між a=x0 на початку і b = xn. Прямокутники мають кінцеві точки на a=x0, x1, x2... x (n-1) та b = xn, розташовані однаково. Висота кожного прямокутника визначається значенням заданої функції в правій кінцевій точці прямокутника. — Рисунок$\PageIndex{3}$: У правій кінцевій точці наближення площі під кривою висота кожного прямокутника визначається значенням функції праворуч від кожного підінтервалу. Зверніть увагу, що наближення правої кінцевої точки відрізняється від наближення лівої кінцевої точки на рис$\PageIndex{2}$.

Графіки на малюнку$\PageIndex{4}$ представляють криву$f(x)=\dfrac{x^2}{2}$. На малюнку$\PageIndex{4b}$ ми ділимо область,$[0,3]$ представлену інтервалом, на шість підінтервалів, кожен шириною$0.5$. Таким чином,$Δx=0.5$. Потім ми формуємо шість прямокутників$x_{i−1}$, малюючи вертикальні лінії перпендикулярно лівій кінцевій точці кожного підінтервалу. Визначаємо висоту кожного прямокутника, обчислюючи$f(x_{i−1})$ для$i=1,2,3,4,5,6.$ інтервалів є$[0,0.5],[0.5,1],[1,1.5],[1.5,2],[2,2.5],[2.5,3]$. Знаходимо площу кожного прямокутника, множивши висоту на ширину. Потім сума прямокутних площ наближається до площі між$f(x)$ і$x$ -віссю. Коли ліві кінцеві точки використовуються для обчислення висоти, ми маємо наближення лівої кінцевої точки. Таким чином,

\ [\ почати {вирівнювати*} A≈L_6 &=\ сума_ {i=1} ^6f (x_ {i−1}) Δх = f (x_0) Δx+F (x_1) Δx+F (x_2) Δx+F (x_3) Δx+F (x_4) Δx+F (x_5) Δх\ [4pt]
&= f (0) 0.5+f (0.5) 0.5+f (1) 0.5+f (1.5) 0.5+f (2) 0.5+f (2.5) 0,5\\ [4pt]
& = (0) 0,5 + (0,125) 0,5+ (1,125) 0,5+ (2) 0.5+ (3,125) 0,5\\ [
4pt] &0+0625 +0,25+0,5625+1+1,5625\\ [4pt]
&=3.4375\,\ текст {одиниці} ^2\ кінець {вирівнювати*}\ nonumber\]

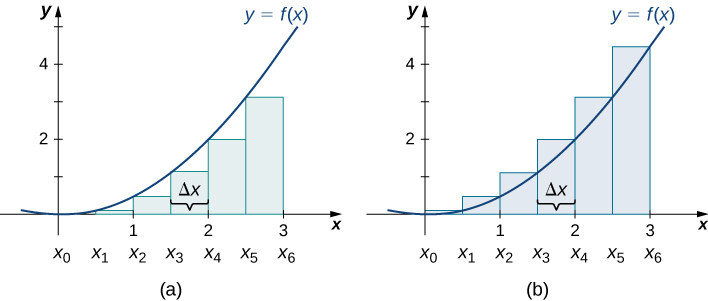
Діаграми пліч-о-пліч, що показують відмінності в апроксимації площі під параболічною кривою з вершиною на початку між методом лівих кінцевих точок (перша діаграма) та методом правих кінцевих точок (друга діаграма). На першій діаграмі прямокутники малюються через парні інтервали (дельта х) під кривою з висотами, визначеними значенням функції в лівих кінцевих точках. На другій діаграмі прямокутники малюються таким же чином, але з висотами, визначеними значенням функції в правильних кінцевих точках. Кінцеві точки в обох розміщені однаково від початку до (3, 0), з позначкою x0 до x6. — Рисунок$\PageIndex{4}$: Методи наближення площі під кривою за допомогою (а) лівих кінцевих точок і (b) правих кінцевих точок.

На малюнку$\PageIndex{4b}$ проводимо вертикальні лінії перпендикулярно$x_i$ таким, що$x_i$ є правою кінцевою точкою кожного підінтервалу, і обчислюємо$f(x_i)$ для$i=1,2,3,4,5,6$. Ми множимо кожен$f(x_i)$ на,$Δx$ щоб знайти прямокутні області, а потім складаємо їх. Це наближення правої кінцевої точки області під$f(x)$. Таким чином,

\ [\ почати {вирівнювати*} A≈R_6 &=\ сума_ {i = 1} ^6f (x_i) Δx=F (x_1) Δx+F (x_2) Δx+F (x_3) Δx+F (x_4) Δx+F (x_5) Δx+F (x_6) Δх\\ [4пт]
= f (0,5) 0.5+f (1) 0.5+f (1.5) 0.5+f (2) 0.5+f (2,5) 0.5+f (3) 0,5\\ [4pt]
& = (0,125) 0,5+ (0.5) 0.5+ (1,125) 0,5+ (3,125) 0,5\\ [4 пт]
&= 0,0625+0,25 +0,5625+1+1,5625+2,25\\ [4pt]
&=5.6875\,\ текст {одиниці} ^2. \ end {вирівнювати*}\ nonumber\]

Приклад$\PageIndex{4}$: Approximating the Area Under a Curve

Використовуйте як наближення лівої, так і правої кінцевої точки, щоб наблизити площу під кривою$f(x)=x^2$ на інтервалі$[0,2]$; використання$n=4$.

Рішення

Спочатку ділимо інтервал$[0,2]$ на$n$ рівні підінтервали. Використання$n=4,\, Δx=\dfrac{(2−0)}{4}=0.5$. Це ширина кожного прямокутника. Інтервали$[0,0.5],[0.5,1],[1,1.5],[1.5,2]$ показані на рис$\PageIndex{5}$. Використовуючи наближення лівої кінцевої точки, висоти є$f(0)=0,\,f(0.5)=0.25,\,f(1)=1,$ і$f(1.5)=2.25.$ тоді,

\[ \begin{align*} L_4 &=f(x_0)Δx+f(x_1)Δx+f(x_2)Δx+f(x_3)Δx \\[4pt] &=0(0.5)+0.25(0.5)+1(0.5)+2.25(0.5) \\[4pt] &=1.75 \,\text{units}^2 \end{align*} \nonumber \]

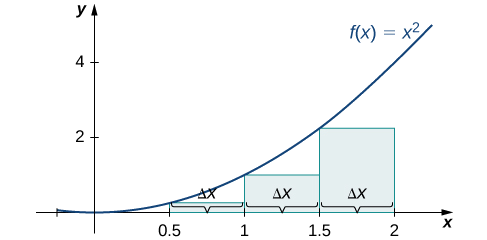
Графік наближення лівої кінцевої точки ділянки під кривою f (x) = x^2 від 0 до 2 з кінцевими точками, розташованими на відстані 0,5 одиниць один від одного. Висоти прямокутника визначаються значеннями функції в їх лівих кінцевих точках. — Рисунок$\PageIndex{5}$: Графік показує наближення лівої кінцевої точки області під$f(x)=x^2$ from$0$ to$2$.

Наближення правої кінцевої точки показано на малюнку$\PageIndex{6}$. Інтервали однакові,$Δx=0.5,$ але тепер використовуйте праву кінцеву точку для обчислення висоти прямокутників. У нас є

\[ \begin{align*} R_4 &=f(x_1)Δx+f(x_2)Δx+f(x_3)Δx+f(x_4)Δx \\[4pt] &=0.25(0.5)+1(0.5)+2.25(0.5)+4(0.5) \\[4pt] &=3.75 \,\text{units}^2 \end{align*} \nonumber \]

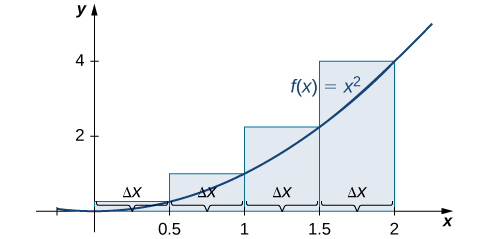
Графік методу наближення правої кінцевої точки площі під кривою f (x) = x^2 від 0 до 2 з кінцевими точками, розташованими на відстані 0,5 одиниць один від одного. Висоти прямокутників визначаються значеннями функції в правильних кінцевих точках. — Малюнок$\PageIndex{6}$: На графіку показано наближення правої кінцевої точки області під$f(x)=x^2$ from$0$ to$2$.

Наближення лівої кінцевої точки є$1.75\,\text{units}^2$; наближення правої кінцевої точки є$3.75 \,\text{units}^2$.

Вправа$\PageIndex{4}$

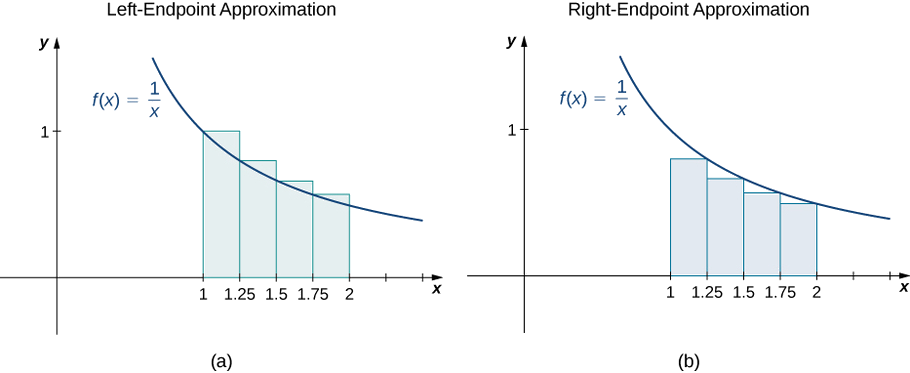
Намалюйте наближення лівої та правої кінцевої точки для$f(x)=\dfrac{1}{x}$$[1,2]$ увімкнено; використання$n=4$. Орієнтуйте площу за допомогою обох методів.

Підказка: Дотримуйтесь стратегії вирішення у прикладі$\PageIndex{4}$ крок за кроком.

Відповідь

Наближення лівої кінцевої точки є$0.7595 \,\text{units}^2$. Наближення правої кінцевої точки є$0.6345 \,\text{units}^2$. Дивіться нижче Медіа.

$Два графіки пліч-о-пліч показують наближення лівої кінцевої точки і наближення правої кінцевої точки області під кривою f (x) = 1/x від 1 до 2 з кінцевими точками, розташованими рівномірно на 0,25 одиниць. Висоти наближення лівої кінцевої точки визначаються значеннями функції в лівих кінцевих точках, а висоту правої кінцевої точки наближення визначають значеннями функції в правих кінцевих точках.$

Дивлячись на рисунок$\PageIndex{4}$ та графіки в прикладі$\PageIndex{4}$, ми можемо побачити, що коли ми використовуємо невелику кількість інтервалів, ні наближення лівої кінцевої точки, ні наближення правої кінцевої точки не є особливо точною оцінкою площі під кривою. Однак, здається логічним, що якщо ми збільшимо кількість балів у нашому розділі, наша оцінка$A$ покращиться. У нас буде більше прямокутників, але кожен прямокутник буде тонше, тому ми зможемо більш точно підігнати прямокутники до кривої.

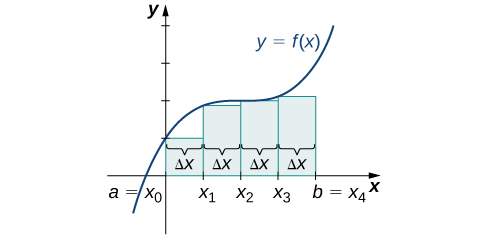
Ми можемо продемонструвати покращене наближення, отримане через менші інтервали на прикладі. Давайте вивчимо ідею збільшення$n$, спочатку в наближенні до лівої кінцевої точки з чотирма прямокутниками, потім вісьмома прямокутниками і, нарешті,$32$ прямокутниками. Потім, давайте зробимо те ж саме в правій кінцевій точці наближення, використовуючи ті ж набори інтервалів, тієї ж кривої області. $\PageIndex{7}$На малюнку показано площу області під кривою$f(x)=(x−1)^3+4$ на інтервалі$[0,2]$ за допомогою наближення лівої кінцевої точки, де$n=4.$ Ширина кожного прямокутника дорівнює

\[Δx=\dfrac{2−0}{4}=\dfrac{1}{2}.\nonumber \]

Площа наближається підсумованими ділянками прямокутників, або

\[L_4=f(0)(0.5)+f(0.5)(0.5)+f(1)(0.5)+f(1.5)0.5=7.5 \,\text{units}^2\nonumber \]

Графік наближення лівої кінцевої точки ділянки під заданою кривою від a = x0 до b=x4. Висоти прямокутників визначаються значеннями функції в лівих кінцевих точках. — Малюнок$\PageIndex{7}$: При наближенні лівої кінцевої точки і діленні області від$a$ до$b$ на чотири рівні проміжки площа під кривою приблизно дорівнює сумі площ прямокутників.

$\PageIndex{8}$На малюнку показана та ж крива, розділена на вісім субінтервалів. Порівнюючи графік з чотирма прямокутниками на малюнку$\PageIndex{7}$ з цим графіком з вісьмома прямокутниками, ми бачимо, що під кривою виявляється менше пробілу, коли$n=8.$ Цей пробіл є площею під кривою, яку ми не можемо включити за допомогою нашого наближення. Площа прямокутників дорівнює

\[L_8=f(0)(0.25)+f(0.25)(0.25)+f(0.5)(0.25)+f(0.75)(0.25)+f(1)(0.25)+f(1.25)(0.25)+f(1.5)(0.25)+f(1.75)(0.25)=7.75 \,\text{units}^2\nonumber \]

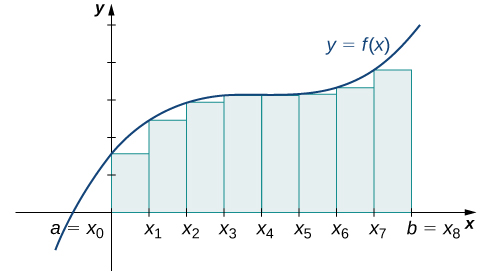
Графік, що показує наближення лівої кінцевої точки для площі під заданою кривою від a=x0 до b = x8. Висоти прямокутників визначаються значеннями функції в лівих кінцевих точках. — Малюнок$\PageIndex{8}$: Область під кривою ділиться на$n=8$ прямокутні ділянки однакової ширини для наближення лівої точки.

Графік на малюнку$\PageIndex{9}$ показує ту ж функцію з$32$ прямокутниками, вписаними під криву. Здається, залишилося мало пробілу. Площа, яку займають прямокутники, дорівнює

\[L_{32}=f(0)(0.0625)+f(0.0625)(0.0625)+f(0.125)(0.0625)+⋯+f(1.9375)(0.0625)=7.9375 \,\text{units}^2.\nonumber \]

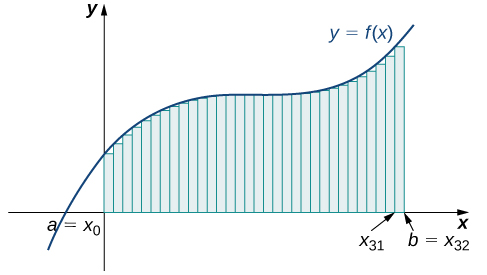
Графік наближення лівої кінцевої точки площі під заданою кривою від a = x0 до b = x32. Висоти прямокутників визначаються значеннями функції в лівих кінцевих точках. — Малюнок$\PageIndex{9}$: Тут$32$ прямокутники вписуються під криву для наближення лівої точки.

Ми можемо провести подібний процес для методу наближення правої точки. Апроксимація правої кінцевої точки тієї ж кривої, використовуючи чотири прямокутники (рис.$\PageIndex{10}$), дає площу

\[R_4=f(0.5)(0.5)+f(1)(0.5)+f(1.5)(0.5)+f(2)(0.5)=8.5 \,\text{units}^2.\nonumber \]

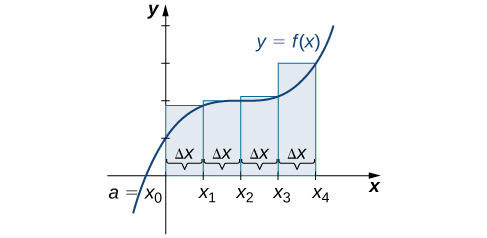
Графік наближення правої кінцевої точки для площі під заданою кривою від x0 до x4. Висоти прямокутників визначаються значеннями функції в правильних кінцевих точках. — Малюнок$\PageIndex{10}$: Тепер ділимо площу під кривою на чотири рівні підінтервали для наближення правої точки.

Розділення області за інтервал$[0,2]$ на вісім прямокутників призводить$Δx=\dfrac{2−0}{8}=0.25.$ до Графік показаний на малюнку$\PageIndex{11}$. Площа - це

\[R_8=f(0.25)(0.25)+f(0.5)(0.25)+f(0.75)(0.25)+f(1)(0.25)+f(1.25)(0.25)+f(1.5)(0.25)+f(1.75)(0.25)+f(2)(0.25)=8.25 \,\text{units}^2\nonumber \]

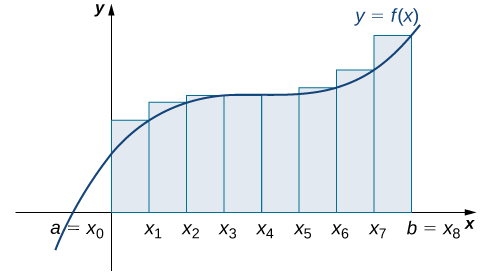
Графік наближення правої кінцевої точки для площі під заданою кривою від a=x0 до B=x8. Висоти прямокутників визначаються значеннями функції в правих кінцевих точках. — Малюнок$\PageIndex{11}$: Тут ми використовуємо наближення правої точки для області, розділеної на вісім рівних підінтервалів.

Останнє, наближення правої кінцевої точки з$n=32$ наближається до фактичної площі (рис.$\PageIndex{12}$). Площа приблизно

\[R_{32}=f(0.0625)(0.0625)+f(0.125)(0.0625)+f(0.1875)(0.0625)+⋯+f(2)(0.0625)=8.0625 \,\text{units}^2\nonumber \]

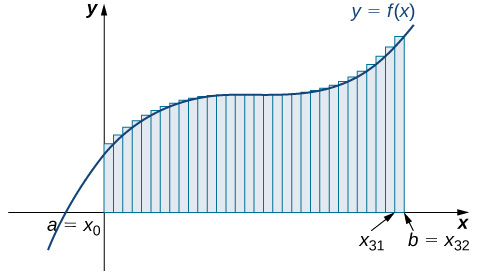
Графік наближення правої кінцевої точки для площі під заданою кривою від a=x0 до b=x32. Висоти прямокутників визначаються значеннями функції в правильних кінцевих точках. — Малюнок$\PageIndex{12}$: Область ділиться на$32$ рівні підінтервали для наближення правої точки.

Виходячи з цих цифр та розрахунків, здається, ми на правильному шляху; прямокутники, здається, наближають площу під кривою краще, оскільки$n$ стає більшою. Крім того, зі$n$ збільшенням, як ліва кінцева точка, так і наближення правої кінцевої точки, здається, наближаються до$8$ площі квадратних одиниць. $\PageIndex{15}$У таблиці наведено числове порівняння методів лівої та правої кінцевої точки. Ідея про те, що наближення площі під кривою стають все кращими і кращими, оскільки$n$ стає все більшими і більшими, дуже важлива, і ми зараз досліджуємо цю ідею більш детально.

Таблиця$\PageIndex{15}$: Зближення значень наближення лівої та правої кінцевої точки зі$n$ збільшенням
Значення$n$	Приблизна площа$L_n$	Приблизна площа$R_n$
\ (n\)» style="вертикальне вирівнювання: середина; ">$n=4$	\ (L_n\)» style="вертикальне вирівнювання: середина; ">$7.5$	\ (R_n\)» style="вертикальне вирівнювання: середина; ">$8.5$
\ (n\)» style="вертикальне вирівнювання: середина; ">$n=8$	\ (L_n\)» style="вертикальне вирівнювання: середина; ">$7.75$	\ (R_n\)» style="вертикальне вирівнювання: середина; ">$8.25$
\ (n\)» style="вертикальне вирівнювання: середина; ">$n=32$	\ (L_n\)» style="вертикальне вирівнювання: середина; ">$7.94$	\ (R_n\)» style="вертикальне вирівнювання: середина; ">$8.06$

Формування сум Рімана

Поки що ми використовували прямокутники для наближення площі під кривою. Висоти цих прямокутників були визначені шляхом оцінки функції в правій або лівій кінцевих точках підінтервалу$[x_{i−1},x_i]$. Насправді немає підстав обмежувати оцінку функції лише одним із цих двох пунктів. Ми могли б оцінити функцію$x^∗_i$ в будь-якій точці підінтервалу$[x_{i−1},x_i]$, і використовувати$f(x^∗_i)$ як висоту нашого прямокутника. Це дає нам оцінку площі форми.

\[A≈\sum_{i=1}^nf(x^∗_i)\,Δx. \nonumber \]

Сума цієї форми називається сумою Рімана, названою на честь математика XIX століття Бернхарда Рімана, який розробив ідею.

Визначення: сума Рімана

$f(x)$Дозволяти визначатися на замкнутому інтервалі$[a,b]$ і нехай$P$ бути будь-який розділ$[a,b]$. $Δx_i$Дозволяти бути ширина кожного підінтервалу$[x_{i−1},x_i]$ і для кожного$i$, нехай$x^∗_i$ буде будь-яка точка в$[x_{i−1},\,x_i]$. Сума Рімана$f(x)$ визначена для як

\[\sum_{i=1}^nf(x^∗_i)\,Δx_i. \nonumber \]

На цьому етапі ми виберемо звичайний розділ$P$, як ми маємо в наших прикладах вище. Це змушує все$Δx_i$ дорівнювати$Δx = \dfrac{b-a}{n}$ будь-якому натуральному числу інтервалів$n$.

Нагадаємо, що з наближеннями лівої та правої кінцевої точки оцінки, здається, стають все кращими та кращими, оскільки$n$ стають більшими та більшими. Те ж саме відбувається і з сумами Рімана. Суми Рімана дають кращі наближення для більших значень$n$. Тепер ми готові визначити площу під кривою в перерахунку на суми Рімана.

Визначення: Площа під кривою

$f(x)$Дозволяти бути неперервна, невід'ємна функція на інтервалі$[a,b]$, і нехай$\displaystyle \sum_{i=1}^nf(x^∗_i)\,Δx$ буде сума Рімана для$f(x)$ з регулярним розділом$P$. Потім площа під кривою$y=f(x)$ на$[a,b]$ задається

\[A=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)\,Δx. \nonumber \]

Дивіться графічну демонстрацію побудови суми Рімана.

Деякі тонкощі тут варто обговорити. По-перше, зауважте, що беручи межу суми трохи відрізняється від взяття межі функції$f(x)$, яка$x$ переходить до нескінченності. Межі сум детально розглядаються в розділі про послідовності та ряди; однак наразі можна припустити, що обчислювальні методи, які ми використовували для обчислення меж функцій, також можуть бути використані для обчислення меж сум.

По-друге, ми повинні розглянути, що робити, якщо вираз сходиться до різних меж для різних варіантів на${x^∗_i}.$ щастя, цього не відбувається. Хоча доказ виходить за рамки цього тексту, можна показати, що якщо$f(x)$ безперервне на замкнутому інтервалі$[a,b]$, то$\displaystyle \lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx$ існує і є унікальним (іншими словами, це не залежить від вибору${x^∗_i}$).

Кілька прикладів ми розглянемо коротко. Але, перш ніж ми це зробимо, давайте займемо хвилинку і поговоримо про деякі конкретні варіанти вибору для${x^∗_i}$. Хоча будь-який вибір${x^∗_i}$ дає нам оцінку площі під кривою, ми не обов'язково знаємо, чи є ця оцінка занадто високою (завищеною) чи занадто низькою (заниженою). Якщо важливо знати, чи є наша оцінка високою чи низькою, ми можемо вибрати наше значення,${x^∗_i}$ щоб гарантувати той чи інший результат.

Якщо ми хочемо переоцінити, наприклад, ми можемо вибрати${x^∗_i}$ таку, що$i=1,2,3,…,n,$$f(x^∗_i)≥f(x)$ для всіх$x∈[x_i−1,x_i]$. Іншими словами, вибираємо${x^∗_i}$ так, що for$i=1,2,3,…,n,$$f(x^∗_i)$ - максимальне значення функції на інтервалі$[x_{i−1},x_i]$. Якщо виділити${x^∗_i}$ таким чином, то сума Рімана$\displaystyle \sum_{i=1}^nf(x^∗_i)Δx$ називається верхньою сумою. Аналогічно, якщо ми хочемо недооцінювати, ми можемо вибрати${x∗i}$ так, що для$i=1,2,3,…,n,$$f(x^∗_i)$ є мінімальним значенням функції на інтервалі$[x_{i−1},x_i]$. У цьому випадку пов'язана сума Рімана називається нижчою сумою. Зверніть увагу, що якщо$f(x)$ або збільшується, або зменшується протягом усього інтервалу$[a,b]$, то максимальне і мінімальне значення функції виникають в кінцевих точках підінтервалів, тому верхня і нижня суми якраз такі ж, як і ліві і праві кінцеві наближення.

Приклад$\PageIndex{5}$: Finding Lower and Upper Sums

Знайти меншу суму для$f(x)=10−x^2$ on$[1,2]$; нехай$n=4$ підінтервали.

Рішення

З$n=4$ перевищенням інтервалу$[1,2], \,Δx=\dfrac{1}{4}$. Ми можемо перерахувати інтервали як$[1,1.25],\,[1.25,1.5],\,[1.5,1.75],$ і$[1.75,2]$. Оскільки функція зменшується за інтервал$[1,2],$ Рисунок показує, що нижча сума отримується за допомогою правильних кінцевих точок.

Графік f (x) = 10 − x^2 від 0 до 2. Він налаштований на наближення правого кінця області, обмеженої кривою та віссю x на [1, 2], позначеної a=x0 до x4. Він показує меншу суму. — Рисунок$\PageIndex{13}$: Графік$f(x)=10−x^2$ налаштований для наближення правої точки області, обмеженої кривою та$x$ віссю -на$[1,2]$, і він показує нижчу суму.

Сума Рімана дорівнює

\ [\ почати {вирівнювати*}\ сума_ {k=1} ^4 (10−x^2) (0.25) &=0,25 [10− (1,25) ^2+10− (1.5) ^2+10− (1,75) ^2+10− (2) ^2]\\ [4pt]
&= 0,25 [8.4375+7.75+6.9375+6]\ [[4pt]
&=7.28\,\ текст {одиниці} ^2. \ end {вирівнювати*}\]

Площа$7.28$$\text{units}^2$ - нижча сума і недооцінка.

Вправа$\PageIndex{5}$

Знайти верхню суму для$f(x)=10−x^2$ on$[1,2]$; нехай$n=4.$
Намалюйте наближення.

Підказка: $f(x)$зменшується$[1,2]$, тому максимальні значення функції виникають у лівих кінцевих точках підінтервалів.

Відповідь

а. верхня сума =$8.0313 \,\text{units}^2.$

б.

$Графік функції f (x) = 10 − x^2 від 0 до 2. Він налаштований для наближення правої кінцевої точки над областю [1,2], яка позначена як a=x0 до x4. Це верхня сума.$

Приклад$\PageIndex{6}$: Finding Lower and Upper Sums for $f(x)=\sin x$

Знайти меншу суму$f(x)=\sin x$ протягом інтервалу$[a,b]=\left[0,\frac{π}{2} \right]$; нехай$n=6.$

Рішення

Давайте спочатку розглянемо графік на малюнку,$\PageIndex{14}$ щоб отримати краще уявлення про цікаву область.

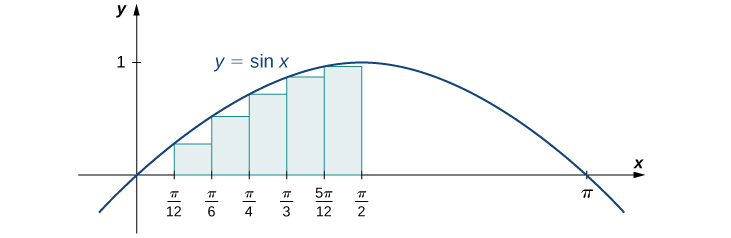
Графік функції y = sin (x) від 0 до pi. Він налаштований для наближення лівої кінцевої точки від 0 до pi/2 та n=6. Це нижча сума. — Малюнок$\PageIndex{14}$: Графік$y=\sin x$ ділиться на шість регіонів:$Δx=\dfrac{π/2}{6}=\dfrac{π}{12}$.

Інтервали становлять$\left[0,\frac{π}{12}\right],\,\left[\frac{π}{12},\frac{π}{6}\right],\,\left[\frac{π}{6},\frac{π}{4}\right],\,\left[\frac{π}{4},\frac{π}{3}\right],\,\left[\frac{π}{3},\frac{5π}{12}\right]$, і$\left[\frac{5π}{12},\frac{π}{2}\right]$. Зверніть увагу,$f(x)=\sin x$ що збільшується на інтервалі$\left[0,\frac{π}{2}\right]$, тому наближення лівої кінцевої точки дає нам нижчу суму. Наближення лівої кінцевої точки - це сума Рімана$\sum_{i=0}^5\sin x_i\left(\tfrac{π}{12}\right)$ .Ми маємо

\[A≈\sin(0)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{12}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{6}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{4}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{3}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{5π}{12}\right)\left(\tfrac{π}{12}\right)\approx 0.863 \,\text{units}^2. \nonumber \]

Вправа$\PageIndex{6}$

За допомогою функції$f(x)=\sin x$ за інтервал$\left[0,\frac{π}{2}\right],$ знайдіть верхню суму; нехай$n=6.$

Підказка: Виконайте кроки з Приклад$\PageIndex{6}$.

Відповідь: $A≈1.125 \,\text{units}^2$

Ключові концепції

Використання сигматичних (підсумовуваних) позначень форми$\displaystyle \sum_{i=1}^na_i$ корисно для вираження довгих сум значень в компактній формі.
Для неперервної функції,$[a,b],$ визначеної протягом інтервалу, процес ділення інтервалу на$n$ рівні частини, розширення прямокутника до графіка функції, обчислення площ ряду прямокутників, а потім підсумовування площ дає наближення площі цієї області.
При використанні звичайної перегородки ширина кожного прямокутника дорівнює$Δx=\dfrac{b−a}{n}$.
Суми Рімана є виразами форми$\displaystyle \sum_{i=1}^nf(x^∗_i)Δx,$ і можуть бути використані для оцінки площі під кривою Наближення$y=f(x).$ лівої та правої кінцевої точки - це спеціальні види сум Рімана, де значення${x^∗_i}$ вибираються відповідно лівою або правою кінцевими точками підінтервалів.
Суми Рімана дозволяють забезпечити велику гнучкість у виборі множини точок,${x^∗_i}$ в яких оцінюється функція, часто з поглядом на отримання нижчої суми або верхньої суми.

Ключові рівняння

Властивості сигма-позначення

\ [\ почати {вирівнювати*}\ сума_ {i = 1} ^nc&=nc\\ [4pt]
\ sum_ {i = 1} ^nca_i &= c\ sum_ {i = 1} ^na_i\
\ [4pt]\ сума {i = 1} ^n (a_i+b_i) &=\ сума {i = 1} ^na_i+\ sum_ {i=1} ^nb_i\\ [4pt]
\ sum_ {i=1} ^n (a_i−b_i) &=\ сума {i=1} ^na_i −\ sum_ {i=1} ^nb_i\\ [4pt]
\ сума {i = 1} ^na_i&=\ sum_ {i=1} ^ma_i+\ sum_ {i=m+1} ^na_i\ end {align*}\]

Суми та степені цілих чисел

\[\sum_{i=1}^ni=1+2+⋯+n=\dfrac{n(n+1)}{2} \nonumber \]

\[\sum_{i=1}^ni^2=1^2+2^2+⋯+n^2=\dfrac{n(n+1)(2n+1)}{6} \nonumber \]

\[\sum_{i=0}^ni^3=1^3+2^3+⋯+n^3=\dfrac{n^2(n+1)^2}{4} \nonumber \]

Наближення лівої кінцевої точки

$A≈L_n=f(x_0)Δx+f(x_1)Δx+⋯+f(x_{n−1})Δx=\displaystyle \sum_{i=1}^nf(x_{i−1})Δx$

Наближення правої кінцевої точки

$A≈R_n=f(x_1)Δx+f(x_2)Δx+⋯+f(x_n)Δx=\displaystyle \sum_{i=1}^nf(x_i)Δx$

Глосарій

наближення лівої кінцевої точки: наближення площі під кривою обчислюється за допомогою лівої кінцевої точки кожного підінтервалу для обчислення висоти вертикальних сторін кожного прямокутника

нижча сума: сума, отримана за допомогою мінімального значення$f(x)$ на кожному підінтервалі

перегородка: сукупність точок, що ділить інтервал на підінтервали

звичайний розділ: розділ, в якому всі підінтервали мають однакову ширину

сума рімана: оцінка площі під кривою форми$A≈\displaystyle \sum_{i=1}^nf(x^∗_i)Δx$

наближення правої кінцевої точки: наближення правої кінцевої точки - це наближення площі прямокутників під кривою з використанням правої кінцевої точки кожного підінтервалу для побудови вертикальних сторін кожного прямокутника

сигма-позначення: (Також, підсумовування позначення) грецька буква сигма ($Σ$) вказує на додавання значень; значення індексу вище і нижче сигми вказують, з чого почати підсумовування і де його закінчити

верхня сума: сума, отримана за допомогою максимального значення$f(x)$ на кожному підінтервалі

Значення\(n\)	Приблизна площа\(L_n\)	Приблизна площа\(R_n\)
\ (n\)» style="вертикальне вирівнювання: середина; ">\(n=4\)	\ (L_n\)» style="вертикальне вирівнювання: середина; ">\(7.5\)	\ (R_n\)» style="вертикальне вирівнювання: середина; ">\(8.5\)
\ (n\)» style="вертикальне вирівнювання: середина; ">\(n=8\)	\ (L_n\)» style="вертикальне вирівнювання: середина; ">\(7.75\)	\ (R_n\)» style="вертикальне вирівнювання: середина; ">\(8.25\)
\ (n\)» style="вертикальне вирівнювання: середина; ">\(n=32\)	\ (L_n\)» style="вертикальне вирівнювання: середина; ">\(7.94\)	\ (R_n\)» style="вертикальне вирівнювання: середина; ">\(8.06\)

Приклад\(\PageIndex{1}\): Using Sigma Notation

Вправа\(\PageIndex{1}\)

Правило: Властивості сигма-позначення

Доказ

Правило: Суми та степені цілих чисел

Приклад\(\PageIndex{2}\): Evaluation Using Sigma Notation

Вправа\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\): Finding the Sum of the Function Values

Вправа\(\PageIndex{3}\)

Визначення: Перегородки

Правило: Наближення лівої кінцевої точки

Правило: наближення правої кінцевої точки

Приклад\(\PageIndex{4}\): Approximating the Area Under a Curve

Вправа\(\PageIndex{4}\)

Визначення: сума Рімана

Визначення: Площа під кривою

Приклад\(\PageIndex{5}\): Finding Lower and Upper Sums

Вправа\(\PageIndex{5}\)

Приклад\(\PageIndex{6}\): Finding Lower and Upper Sums for \(f(x)=\sin x\)

Вправа\(\PageIndex{6}\)