5.3: Суми Рімана

У попередньому розділі ми визначили певний інтеграл функції, яка буде$[a,b]$ знаковою областю між кривою та$x$ віссю —. Деякі області були простими для обчислення; ми закінчили розділ з областю, площа якої не була простою для обчислення. У цьому розділі ми розробляємо методику пошуку таких напрямків.

Фундаментальна техніка обчислення полягає в тому, щоб спочатку відповісти на дану задачу з наближенням, потім уточнити це наближення, щоб зробити його кращим, а потім використовувати межі в процесі уточнення, щоб знайти точну відповідь. Це саме те, що ми тут і будемо робити.

Розглянемо область, наведену на малюнку$\PageIndex{1}$, яка є площею під$y=4x-x^2$ на$[0,4]$. Що таке підписана територія цього регіону — тобто що таке$\int_0^4(4x-x^2)dx$?

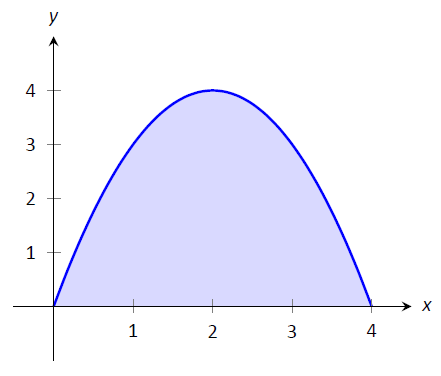
Малюнок$\PageIndex{1}$: Графік$f(x) = 4x-x^2$. Яка площа затіненої області?

Починаємо з наближення. Ми можемо оточити область прямокутником висотою і шириною 4 і знайти площу приблизно 16 квадратних одиниць. Це, очевидно, надмірне наближення; ми включаємо область в прямокутник, який не знаходиться під параболою.

Маємо наближення площі, використовуючи один прямокутник. Як ми можемо вдосконалити наше наближення, щоб зробити його кращим? Ключем до цього розділу є така відповідь: використовуйте більше прямокутників.

Давайте використаємо 4 прямокутника однакової ширини 1. Це розділяє інтервал$[0,4]$ на 4 підінтервали,$[0,1]$,$[1,2]$,$[2,3]$ і$[3,4]$. На кожному підінтервалі намалюємо прямокутник.

Існує три загальні способи визначення висоти цих прямокутників: Правило лівої руки, Правило правої руки та Правило середньої точки. Правило лівої руки говорить, щоб оцінити функцію в лівій кінцевій точці підінтервалу і зробити прямокутник такої висоти. На малюнку прямокутник$\PageIndex{2}$, намальований на інтервалі,$[2,3]$ має висоту, визначену правилом лівої руки; він має висоту$f(2)$. (Прямокутник позначений як «LHR».)

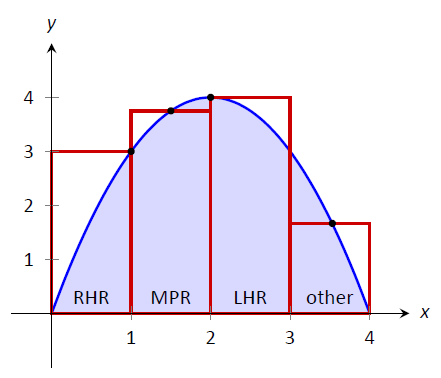
Малюнок$\PageIndex{2}$:$\int_0^4(4x-x^2)dx$ Апроксимація за допомогою прямокутників. Висоти прямокутників визначаються з використанням різних правил.

Правило правої руки говорить протилежне: на кожному підінтервалі оцініть функцію в правій кінцевій точці і зробіть прямокутник такої висоти. На малюнку намальований прямокутник$[0,1]$ малюється за допомогою його висоти; цей прямокутник позначений$f(1)$ як «RHR».

Правило середньої точки говорить, що на кожному підінтервалі оцініть функцію в середній точці і зробіть прямокутник такої висоти. Прямокутник, намальований на,$[1,2]$ був зроблений за допомогою Midpoint Rule, з висотою$f(1.5)$. Цей прямокутник позначений як «MPR».

Це три найпоширеніших правила визначення висот наближених прямокутників, але один не змушений використовувати один з цих трьох методів. Прямокутник$[3,4]$ має висоту приблизно$f(3.53)$, дуже близько до правила середньої точки. Вона була підібрана так, щоб площа прямокутника точно дорівнювала площі області під$f$ на$[3,4]$. (Пізніше ви також зможете зрозуміти, як це зробити.)

Наступний приклад наблизить значення$\int_0^4 (4x-x^2)dx$ використання цих правил.

Приклад$\PageIndex{1}$: Using the Left Hand, Right Hand and Midpoint Rules

Приблизно значення$\int_0^4 (4x-x^2)dx$ використання правила лівої руки, правила правої руки та правила середньої точки, використовуючи 4 однаково розташовані підінтервали.

Рішення

{Ми$[0,4]$ розбиваємо інтервал на чотири підінтервали, як і раніше. На малюнку$\PageIndex{3}$ ми бачимо 4 прямокутники, намальовані$f(x) = 4x-x^2$ за допомогою правила лівої руки. (Площі прямокутників наведені на кожному малюнку.)

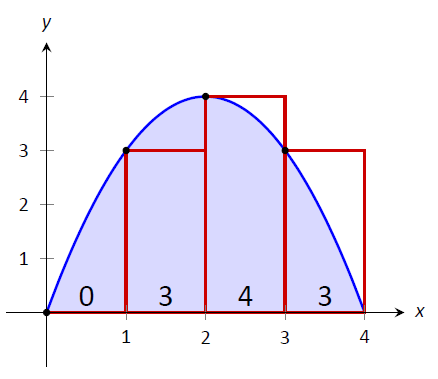
Малюнок$\PageIndex{3}$: Апроксимація$\int_0^4(4x-x^2)dx$ за допомогою правила лівої руки у прикладі$\PageIndex{1}$

Зверніть увагу, як у першому$[0,1]$ підінтервалі прямокутник має висоту$f(0)=0$. Ми складаємо області кожного прямокутника ($\times$ширина висоти) для нашого наближення правила лівої руки:

$$\begin{align} f(0)\cdot 1 + f(1)\cdot 1+ f(2)\cdot 1+f(3)\cdot 1 &=\\ 0+3+4+3&= 10. \end{align}$$

$\PageIndex{4}$На малюнку показано 4 прямокутника, намальовані за$f$ допомогою правила правої руки; зверніть увагу, як$[3,4]$ підінтервал має прямокутник висотою 0.

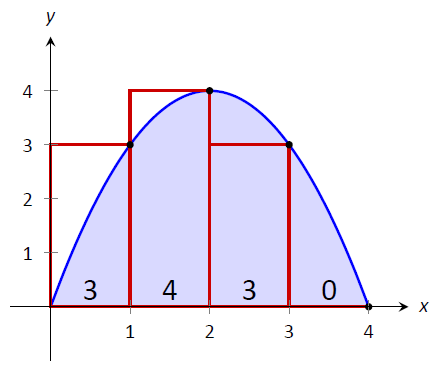
Малюнок$\PageIndex{4}$: Апроксимація$\int_0^4(4x-x^2)dx$ за допомогою правила правої руки у прикладі$\PageIndex{1}$

У цьому прикладі ці прямокутники здаються дзеркальним відображенням тих, що знаходяться на малюнку$\PageIndex{3}$. (Це пов'язано з симетрією нашої затіненої області.) Наше наближення дає ту ж відповідь, що і раніше, хоча і обчислюється по-іншому:

$$\begin{align} f(1)\cdot 1 + f(2)\cdot 1+ f(3)\cdot 1+f(4)\cdot 1 &=\\ 3+4+3+0&= 10. \end{align}$$

$\PageIndex{5}$На малюнку показано 4 прямокутника, намальовані за$f$ допомогою правила середньої точки.

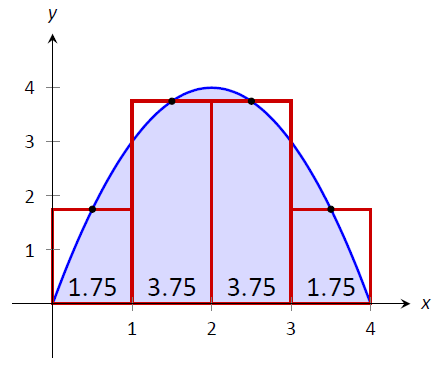
Малюнок$\PageIndex{5}$: Апроксимація$\int_0^4(4x-x^2)dx$ за допомогою правила середньої точки у прикладі$\PageIndex{1}$

Це дає наближення$\int_0^4(4x-x^2)dx$ як:

$$\begin{align} f(0.5)\cdot 1 + f(1.5)\cdot 1+ f(2.5)\cdot 1+f(3.5)\cdot 1 &=\\ 1.75+3.75+3.75+1.75&= 11. \end{align}$$

Наші три методи забезпечують два наближення$\int_0^4(4x-x^2)dx$: 10 і 11.

Позначення підсумовування

Важко сказати в цей момент, яке краще наближення: 10 або 11? Ми можемо продовжувати вдосконалювати наше наближення, використовуючи більше прямокутників. Однак позначення може стати громіздким, оскільки ми складаємо довші та довші списки чисел. Для покращення цієї задачі введено підсумовувальні позначення.

Припустимо, ми хочемо скласти список чисел$a_1$,,$a_2$$a_3$,\ ldots,$a_9$. Замість того, щоб писати

$a_1+a_2+a_3+a_4+a_5+a_6+a_7+a_8+a_9,\]

використовуємо підсумовувальні позначення і пишемо

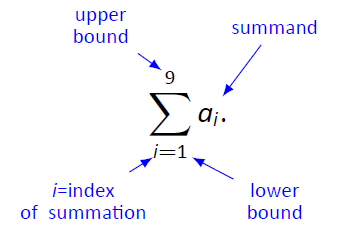
Малюнок$\PageIndex{6}$: Розуміння позначень підсумовування

Сигма верхнього регістру являє собою термін «сума». Індекс підсумовування в цьому прикладі є$i$; можна використовувати будь-який символ. За умовністю індекс приймає тільки ціле значення між (і включно) нижньою і верхньою межею.

Давайте потренуємося використовувати ці позначення.

Приклад$\PageIndex{2}$: Using summation notation

Нехай числа$\{a_i\}$ будуть визначені як$a_i = 2i-1$ для цілих чисел$i$, де$i\geq 1$. Отже$a_1 = 1$,$a_2 = 3$$a_3 = 5$, і т.д. (Вихідні дані - натуральні непарні цілі числа). Оцініть наступні підсумовування:

$$1.\ \sum_{i=1}^6 a_i \qquad\qquad\qquad 2.\ \sum_{i=3}^7 (3a_i-4)\qquad\qquad \qquad 3.\ \sum_{i=1}^4 (a_i)^2$$

Рішення

1. $$\begin{align} \sum_{i=1}^6 a_i &= a_1+a_2+a_3+a_4+a_5+a_6\\ &= 1+3+5+7+9+11 \\ &= 36.\end{align}$$
2. Зверніть увагу, що початкове значення відрізняється від 1: $$\begin{align} \sum_{i=3}^7 a_i &= (3a_3-4)+(3a_4-4)+(3a_5-4)+(3a_6-4)+(3a_7-4) \\ &= 11+17+23+29+35 \\ &= 115. \end{align}$$
3. $$\begin{align} \sum_{i=1}^4 (a_i)^2 &= (a_1)^2+(a_2)^2+(a_3)^2+(a_4)^2\\ &= 1^2+3^2+5^2+7^2 \\ &= 84 \end{align}$$

Може здатися дивним підкреслити новий, стислий спосіб написання підсумовувань лише для того, щоб написати кожен термін, коли ми їх складаємо. Це так. Наступна теорема дає деякі властивості підсумовувань, які дозволяють працювати з ними без написання окремих термінів. Приклади будуть слідувати.

Теорема$\PageIndex{1}$: Properties of Summations

1. $\sum_{i=1}^n c = c\cdot n$, Де$c$ константа.
2. $\sum_{i=m}^n (a_i\pm b_i) = \sum_{i=m}^n a_i \pm \sum_{i=m}^n b_i$
3. $\sum_{i=m}^n c\cdot a_i = c\cdot\sum_{i=m}^n a_i$
4. $\sum_{i=m}^j a_i + \sum_{i=j+1}^n a_i = \sum_{i=m}^n a_i$
5. $\sum_{i=1}^n i = \frac{n(n+1)}2$
6. $\sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}6$
7. $\sum_{i=1}^n i^3 = \left(\frac{n(n+1)}2\right)^2$

Приклад$\PageIndex{3}$: Evaluating summations using Theorem$\PageIndex{1}$

Переглянути приклад$\PageIndex{2}$ і, використовуючи теорему$\PageIndex{1}$, оцінити

$$\sum_{i=1}^6 a_i = \sum_{i=1}^6 (2i-1).$$

Рішення

$$\begin{align} \sum_{i=1}^6 (2i-1) & = \sum_{i=1}^6 2i - \sum_{i=1}^6 (1)\\ &= \left(2\sum_{i=1}^6 i \right)- 6 \\ &= 2\frac{6(6+1)}{2} - 6 \\ &= 42-6 = 36 \end{align}$$

Ми отримали однакову відповідь, не виписуючи всі шість термінів. При роботі з невеликими розмірами$n$, це може бути швидше, щоб виписати терміни від руки. Однак теорема неймовірно$\PageIndex{1}$ важлива при роботі з великими сумами, як ми скоро побачимо.

Ріман Суми

Розглянемо ще раз$\int_0^4(4x-x^2)dx$. Ми наблизимо цей певний інтеграл, використовуючи 16 однаково розташованих підінтервалів та правилом правої руки у прикладі$\PageIndex{4}$. Перш ніж це зробити, він заплатить, щоб зробити деяку ретельну підготовку.

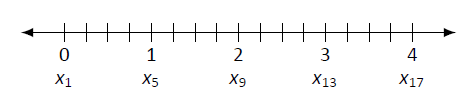
Малюнок$\PageIndex{7}$:$[0,4]$ Розділення на 16 однаково розташованих підінтервалів.

$\PageIndex{7}$На малюнку показана числова лінія$[0,4]$ розділена на 16 однаково розташованих підінтервалів. Позначимо$0$ як$x_1$; ми позначили значення$x_5$$x_9$,$x_{13}$ і$x_{17}$. Ми могли б позначити їх усіх, але фігура буде переповнена. Хоча легко зрозуміти$x_{10} = 2.25$, що, в цілому, ми хочемо метод визначення величини$x_i$ без консультації з фігурою. Розглянемо:

Так$x_{10} = x_1 + 9(4/16) = 2.25.$

Якби ми$[0,4]$ розділили на 100 однаково розташованих підінтервалів, кожен підінтервал мав би довжину$\Delta x=4/100 = 0.04$. Ми могли б обчислити$x_{32}$ як

$ х_ {32} = х_1 + 31 (4/100) = 1,24.\]

(Це було набагато швидше, ніж спочатку створити ескіз.)

Враховуючи будь-який підрозділ$[0,4]$, перший підінтервал є$[x_1,x_2]$; другий є$[x_2,x_3]$;$i^\text{ th}$ підінтервал є$[x_i,x_{i+1}]$.

При використанні правила лівої руки висота$i^\text{ th}$ прямокутника буде$f(x_i)$.

При використанні Правила правої руки висота$i^\text{ th}$ прямокутника буде$f(x_{i+1})$.

При використанні правила середньої точки висота$i^\text{ th}$ прямокутника буде$f\left(\frac{x_i+x_{i+1}}2\right)$.

Таким чином, наближення$\int_0^4(4x-x^2)dx$ з 16 однаково розташованими підінтервалами можна виразити наступним чином, де$\Delta x = 4/16 = 1/4$:

Правило лівої руки:$\sum_{i=1}^{16} f(x_i)\Delta x$

Правило правої руки:$\sum_{i=1}^{16} f(x_{i+1})\Delta x$

Правило середньої точки:$\sum_{i=1}^{16} f\left(\frac{x_i+x_{i+1}}2\right)\Delta x$

Ми використовуємо ці формули в наступних двох прикладах. Наступний приклад дозволяє нам практикувати використання правила правої руки та формули підсумовування, введені в теоремі.$\PageIndex{1}$

Приклад$\PageIndex{4}$: Approximating definite integrals using sums

Наближені$\int_0^4(4x-x^2)dx$ за допомогою правила правої руки та формули підсумовування з 16 і 1000 однаково віддаленими інтервалами.

Рішення

Використовуючи формулу, отриману раніше, використовуючи 16 однакових інтервалів та Правило Правої руки, ми можемо наблизити певний інтеграл як

$$\sum_{i=1}^{16}f(x_{i+1})\Delta x.$$

У нас є$\Delta x = 4/16 = 0.25$. З тих пір$x_i = 0+(i-1)\Delta x$, у нас є

$$\begin{align}x_{i+1} &= 0 + \big((i+1)-1\big)\Delta x \\ &= i\Delta x \end{align}$$

Використовуючи формули підсумовування, розглянемо:

$$\begin{align} \int_0^4 (4x-x^2)dx &\approx \sum_{i=1}^{16} f(x_{i+1})\Delta x \\ &= \sum_{i=1}^{16} f(i\Delta x) \Delta x\\ &= \sum_{i=1}^{16} \big(4i\Delta x - (i\Delta x)^2\big)\Delta x\\ &= \sum_{i=1}^{16} (4i\Delta x^2 - i^2\Delta x^3)\\ &= (4\Delta x^2)\sum_{i=1}^{16} i - \Delta x^3 \sum_{i=1}^{16} i^2 \\ &= (4\Delta x^2)\frac{16\cdot 17}{2} - \Delta x^3 \frac{16(17)(33)}6 \\ &= 4\cdot 0.25^2\cdot 136-0.25^3\cdot 1496\\ &=10.625 \end{align}$$

Ми змогли підсумувати площі 16 прямокутників з дуже невеликою кількістю обчислень. На$\PageIndex{8}$ малюнку функція та 16 прямокутників намальовані графіки. У той час як деякі прямокутники наближають площу, інші під - наближають площу (приблизно на таку ж суму). Таким чином, наша приблизна площа 10,625, швидше за все, є досить хорошим наближенням.

Зверніть увагу на рівняння$\PageIndex{31}$; змінивши 16 на 1,000 (і відповідним чином змінивши значення$\Delta x$), ми можемо використовувати це рівняння, щоб підсумувати 1000 прямокутників!

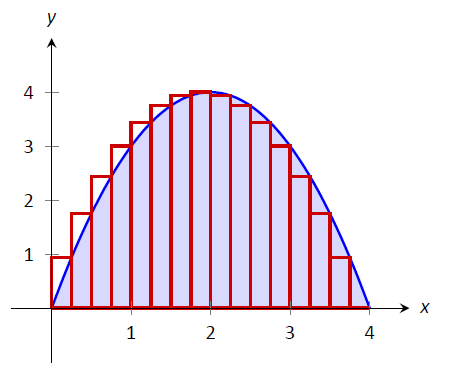
Малюнок$\PageIndex{8}$:$\int_0^4(4x-x^2)dx$ Апроксимація правилом правої руки та 16 рівномірно розташованих підінтервалів.

Ми робимо це тут, переходячи від початкового summand до еквівалента Рівняння,$\PageIndex{31}$ щоб заощадити місце. Зауважте, що$\Delta x = 4/1000 = 0.004$.

$$\begin{align} \int_0^4 (4x-x^2)dx &\approx \sum_{i=1}^{1000} f(x_{i+1})\Delta x \\&= (4\Delta x^2)\sum_{i=1}^{1000} i - \Delta x^3 \sum_{i=1}^{1000} i^2 \\&= (4\Delta x^2)\frac{1000\cdot 1001}{2} - \Delta x^3 \frac{1000(1001)(2001)}6 \\&= 4\cdot 0.004^2\cdot 500500-0.004^3\cdot 333,833,500\\ &=10.666656 \end{align}$$

Використовуючи багато, багато прямокутників, ми маємо, ймовірно, хороше наближення$\int_0^4 (4x-x^2) dx$. Тобто,

$\ int_0^4 (4x-x^2) х\ приблизно 10,66656.\]

Перед наведеним вище прикладом ми вказували, як виглядали підсумки для правил лівої руки, правої руки та середньої точки. Кожен мав однакову основну структуру, яка була:

1. кожен прямокутник має однакову ширину, яку ми називали$\Delta x$, і
2. Висота кожного прямокутника визначається шляхом оцінки$f$ в певній точці кожного підінтервалу. Наприклад, правило лівої руки стверджує, що висота кожного прямокутника визначається шляхом оцінки$f$ в лівій кінцевій точці підінтервалу, на якому живе прямокутник.

Можна розділити інтервал$[a,b]$ з підінтервалами, які не мали однакового розміру. Ми посилаємося на довжину першого підінтервалу як$\Delta x_1$, довжина другого підінтервалу як$\Delta x_2$, і так далі, даючи довжину$i^\text{ th}$ субінтервалу як$\Delta x_i$. Крім того, можна визначити висоту кожного прямокутника, оцінюючи$f$ точку\ emph {any} у$i^\text{ th}$ підінтервалі. Ми посилаємося на точку, вибрану в першому підінтервалі як$c_1$, точку, взяту у другому підінтервалі як$c_2$, і так далі, з$c_i$ представленням точки, взятої в$i^\text{ th}$ підінтервалі. Таким чином, висота$i^\text{ th}$ підінтервалу буде$f(c_i)$, а площа$i^\text{ th}$ прямокутника буде$f(c_i)\Delta x_i$.

Підсумовування прямокутників з площею$f(c_i)\Delta x_i$ названі на честь математика Георга Фрідріха Бернхарда Рімана, як дано в наступному визначенні.

Визначення$\PageIndex{1}$: Riemann Sum

$f$Дозволяти визначатися на замкнутому інтервалі$[a,b]$ і нехай$\Delta x$ бути розділом$[a,b]$, з

$a=x_1 < x_2 <\ ldots < x_n < x_ {n+1} =б.\]

Нехай$\Delta x_i$ позначають довжину$i^\text{ th}$ підінтервалу$[x_i,x_{i+1}]$ і нехай$c_i$ позначають будь-яке значення в$i^\text{ th}$ підінтервалі.

Сума

$$\ сума_ {i=1} ^n f (c_i)\ Дельта x_i\]

це сума Riemann від$f$$[a,b]$.

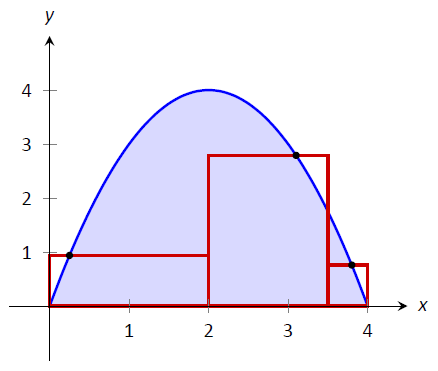
Малюнок$\PageIndex{9}$: Приклад загальної суми Рімана до наближення$\int_0^4(4x-x^2)dx$

$\PageIndex{9}$На малюнку показані наближені прямокутники суми Рімана$\int_0^4(4x-x^2)dx$. Хоча прямокутники в цьому прикладі погано наближаються до затіненої області, вони демонструють, що підінтервальні ширини можуть змінюватися, а висоту прямокутників можна визначити, не дотримуючись певного правила.

«Зазвичай» суми Рімана обчислюються за допомогою одного з трьох методів, які ми запровадили. Рівномірність побудови полегшує обчислення. Перш ніж працювати з іншим прикладом, давайте підсумуємо деякі з того, що ми дізналися зручним способом.

Ключова ідея 8: Поняття суми Рімана

Розглянемо$\int_a^b f(x) dx \approx \sum_{i=1}^n f(c_i)\Delta x_i.$

1. Коли$n$ підінтервали мають однакову довжину,$\Delta x_i = \Delta x = \frac{b-a}n.$
2. $i^\text{ th}$Термін дії перегородки - це$x_i = a + (i-1)\Delta x$. (Це робить$x_{n+1} = b$.)
3. Підсумовування правила лівої руки:$\sum_{i=1}^n f(x_i)\Delta x$.
4. Підсумовування правилом правої руки:$\sum_{i=1}^n f(x_{i+1})\Delta x$.
5. Підсумовування правила середньої точки:$\sum_{i=1}^n f\left(\frac{x_i+x_{x+1}}{2}\right)\Delta x$.

Давайте зробимо ще один приклад.

Приклад$\PageIndex{5}$: Approximating definite integrals with sums

Приблизно,$\int_{-2}^3 (5x+2)dx$ використовуючи правило середньої точки та 10 однаково розташованих інтервалів.

Рішення

Слідуючи ключовій ідеї 8, ми маємо

$$\Delta x = \frac{3 - (-2)}{10} = 1/2 \quad \text{and} \quad x_i = (-2) + (1/2)(i-1) = i/2-5/2.$$

Оскільки ми використовуємо правило середньої точки, нам також знадобиться$x_{i+1}$ і$\frac{x_i+x_{i+1}}2$. З тих пір$x_i = i/2-5/2$,$x_{i+1} = (i+1)/2 - 5/2 = i/2 -2$. Це дає

$$\frac{x_i+x_{i+1}}2 = \frac{(i/2-5/2) + (i/2-2)}{2} = \frac{i-9/2}{2} = i/2 - 9/4.$$

Зараз ми будуємо суму Рімана і обчислюємо її значення за допомогою формул підсумовування.

$$\begin{align} \int_{-2}^3 (5x+2)dx &\approx \sum_{i=1}^{10} f\left(\frac{x_i+x_{i+1}}{2}\right)\Delta x \\ &= \sum_{i=1}^{10} f(i/2 - 9/4)\Delta x \\ &= \sum_{i=1}^{10} \big(5(i/2-9/4) + 2\big)\Delta x\\ &= \Delta x\sum_{i=1}^{10}\left[\left(\frac{5}{2}\right)i - \frac{37}{4}\right]\\ &= \Delta x\left(\frac{5}2\sum_{i=1}^{10} (i) - \sum_{i=1}^{10}\left(\frac{37}{4}\right)\right) \\&= \frac12\left(\frac52\cdot\frac{10(11)}{2} - 10\cdot\frac{37}4\right) \\ &= \frac{45}2 = 22.5 \end{align}$$

Зверніть увагу на графік$f(x) = 5x+2$ на рис$\PageIndex{10}$. Регіони, площа яких обчислюється певним інтегралом, є трикутниками, тобто ми можемо знайти точну відповідь без методів підсумовування. Ми виявляємо, що точна відповідь дійсно 22,5. Однією з сильних сторін правила середньої точки є те, що часто кожен прямокутник включає область, яку не слід рахувати, але пропускає іншу область, яка повинна. Коли розмір розділу невеликий, ці дві суми приблизно рівні, і ці помилки майже «скасовують один одного». У цьому прикладі, оскільки наша функція є рядком, ці помилки точно рівні, і вони скасовують один одного, даючи нам точну відповідь.

Зауважте також, що коли функція від'ємна, прямокутники мають «негативну» висоту. Коли ми обчислюємо площу прямокутника, ми використовуємо$f(c_i)\Delta x$; коли$f$ негативна, площа зараховується як негативна.

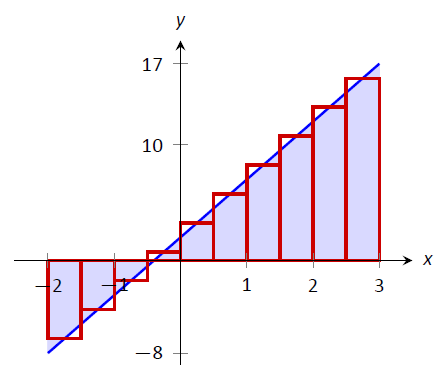
Малюнок$\PageIndex{10}$: Апроксимація$\int_{-2}^3 (5x+2)dx$ за допомогою правила середньої точки та 10 рівномірно розташованих підінтервалів у прикладі$\PageIndex{5}$.

Зверніть увагу в попередньому прикладі, що в той час як ми використовували 10 однаково розставлених інтервалів, число «10" не грало великої ролі в розрахунках до самого кінця. Математики люблять абстрактні ідеї; давайте наблизимо площу іншого регіону за допомогою$n$ підінтервалів, де ми не вказуємо значення$n$ до самого кінця.

Приклад$\PageIndex{6}$: Approximating definite integrals with a formula, using sums

Повернутися$\int_0^4(4x-x^2)dx$ ще раз. Наближається цей певний інтеграл, використовуючи Правило правої руки з$n$ однаково розставленими підінтервалами.

Рішення

Використовуючи Key Idea 8, ми знаємо$\Delta x = \frac{4-0}{n} = 4/n$. Ми також знаходимо$x_i = 0 + \Delta x(i-1) = 4(i-1)/n$. Правило правої руки використовує$x_{i+1}$, який є$x_{i+1} = 4i/n$.

Побудуємо суму Правила правої руки Рімана наступним чином. Обов'язково уважно стежте за кожним кроком. Якщо ви застрягли, і не розумієте, як один рядок переходить до наступного, можете перейти до результату і розглянути, як цей результат використовується. Ви повинні повернутися, хоча, і працювати через кожен крок для повного розуміння.

$$\begin{align} \int_0^4(4x-x^2)dx &\approx \sum_{i=1}^n f(x_{i+1})\Delta x \\ &= \sum_{i=1}^n f\left(\frac{4i}{n}\right) \Delta x \\ &= \sum_{i=1}^n \left[4\frac{4i}n-\left(\frac{4i}n\right)^2\right]\Delta x\\ &= \sum_{i=1}^n \left(\frac{16\Delta x}{n}\right)i - \sum_{i=1}^n \left(\frac{16\Delta x}{n^2}\right)i^2 \\ &= \left(\frac{16\Delta x}{n}\right)\sum_{i=1}^n i - \left(\frac{16\Delta x}{n^2}\right)\sum_{i=1}^n i^2 \\ &= \left(\frac{16\Delta x}{n}\right)\cdot \frac{n(n+1)}{2} - \left(\frac{16\Delta x}{n^2}\right)\frac{n(n+1)(2n+1)}{6} &\left(\text{recall $\Delta x = 4/n$}\right)\\ &=\frac{32(n+1)}{n} - \frac{32(n+1)(2n+1)}{3n^2} &\text{(now simplify)} \\ &= \frac{32}{3}\left(1-\frac{1}{n^2}\right) \end{align}$$

В результаті виходить дивовижна, проста у використанні формула. Щоб наблизити певний інтеграл з 10 однаково розташованими підінтервалами та правилом правої руки, встановити$n=10$ та обчислити

$\ int_0^4 (4x-x^2) дх\ приблизно\ розриву {32} {3}\ ліворуч (1-\ розриву {1} {10 ^ 2}\ праворуч) = 10.56.\]

Нагадаємо, як раніше ми наближали певний інтеграл з 4 підінтервалами; при$n=4$, формула дає 10, наша відповідь, як і раніше.

Тепер легко наблизити інтеграл з 1,000,000 підінтервалів! Ручні калькулятори будуть округлити відповідь трохи передчасно даючи відповідь$10.66666667$. (Фактична відповідь є$10.666666666656$.)

Тепер ми робимо важливий стрибок. До цього моменту наша математика обмежувалася геометрією та алгеброю (пошук областей та маніпулювання виразами). Тепер застосовуємо\ textit {обчислення}. Для будь-якого\ textit {finite}$n$, ми знаємо, що

$\ int_0^4 (4x-x^2) дх\ приблизно\ розриву {32} {3}\ ліворуч (1-\ розриву {1} {n^2}\ праворуч).\]

Як здоровий глузд, так і математика високого рівня говорять нам, що коли$n$ стає великим, наближення стає кращим. Насправді, якщо взяти ліміт як$n\rightarrow \infty$, ми отримаємо точну область, описану$\int_0^4 (4x-x^2)dx$. Тобто,

$$\begin{align} \int_0^4 (4x-x^2)dx &= \lim_{n\rightarrow \infty} \frac{32}{3}\left(1-\frac{1}{n^2}\right) \\ &= \frac{32}{3}\left(1-0\right)\\ &= \frac{32}{3} = 10.\overline{6}\end{align}$$

Це фантастичний результат. Розглядаючи$n$ рівновіддалені підінтервали, отримано формулу наближення певного інтеграла, який задіяв нашу змінну$n$. Коли$n$ зростає велика - без обмежень - помилка зменшується до нуля, і ми отримуємо точну площу.

Цей розділ розпочався з фундаментальної методики обчислення: зробіть наближення, уточніть наближення, щоб зробити його кращим, а потім використовуйте обмеження в процесі уточнення, щоб отримати точну відповідь. Це саме те, що ми щойно зробили.

Давайте практикуємо це ще раз.

Приклад$\PageIndex{7}$: Approximating definite integrals with a formula, using sums

Знайдіть формулу, яка наближається$\int_{-1}^5 x^3dx$ за допомогою Правила правої руки та$n$ однаково розставлених підінтервалів, а потім візьміть межу,$n\to\infty$ щоб знайти точну площу.

Рішення

Слідуючи ключовій ідеї 8, ми маємо$\Delta x = \frac{5-(-1)}{n} = 6/n$. У нас є$x_i = (-1) + (i-1)\Delta x$; як правило правої руки використовує$x_{i+1}$, ми маємо$x_{i+1} = (-1) + i\Delta x$.

Сума Рімана, що відповідає правилу правої руки, є (з подальшим спрощенням):

$$\begin{align}\int_{-1}^5 x^3dx &\approx \sum_{i=1}^n f(x_{i+1})\Delta x \\ &= \sum_{i=1}^n f(-1+i\Delta x)\Delta x \\ &= \sum_{i=1}^n (-1+i\Delta x)^3\Delta x \\&= \sum_{i=1}^n \big((i\Delta x)^3 -3(i\Delta x)^2 + 3i\Delta x -1\big)\Delta x \quad \text{\scriptsize (now distribute $\Delta x$)} \\ &= \sum_{i=1}^n \big(i^3\Delta x^4 - 3i^2\Delta x^3 + 3i\Delta x^2 -\Delta x\big) \quad \text{\scriptsize (now split up summation)}\\ &= \Delta x^4 \sum_{i=1}^ni^3 -3\Delta x^3 \sum_{i=1}^n i^2+ 3\Delta x^2 \sum_{i=1}^n i - \sum_{i=1}^n \Delta x \\ &= \Delta x^4 \left(\frac{n(n+1)}{2}\right)^2 -3\Delta x^3 \frac{n(n+1)(2n+1)}{6}+ 3\Delta x^2 \frac{n(n+1)}{2} - n\Delta x \\ \text{(use $\Delta x = 6/n$)}\\ &= \frac{1296}{n^4}\cdot\frac{n^2(n+1)^2}{4} - 3\frac{216}{n^3}\cdot\frac{n(n+1)(2n+1)}{6} + 3\frac{36}{n^2}\frac{n(n+1)}2 -6 \\ \text{(now do a sizable amount of algebra to simplify)}\\ &=156 + \frac{378}n + \frac{216}{n^2} \end{align}$$

Знову ми знайшли компактну формулу для наближення певного інтеграла з$n$ рівновіддаленими підінтервалами та правилом правої руки. Використовуючи 10 підінтервалів, ми маємо наближення$195.96$ (ці прямокутники наведені на рис$\PageIndex{11}$. Використання$n=100$ дає наближення$159.802$.

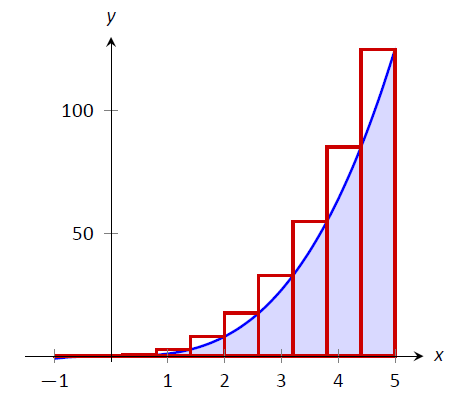
Малюнок$\PageIndex{11}$: Апроксимація$\int_{-1}^5 x^3dx$ за допомогою правила правої руки та 10 рівномірно розташованих підінтервалів.

Тепер знайдіть точну відповідь, використовуючи ліміт:

$\ int_ {-1} ^5 x^3dx =\ lim_ {n\ to\ infty}\ ліворуч (156 +\ frac {378} n +\ frac {216} {n^2}\ праворуч) = 156.\]

Межі сум Рімана

Ми використовували ліміти для оцінки точно заданих певних меж. Чи завжди це спрацює? Ми покажемо, враховуючи не дуже—обмежувальні умови, що так, це завжди працюватиме.

Попередні два приклади продемонстрували, як таке вираз, як

$$\ сума_ {i=1} ^n f (x_ {i+1})\ Дельта х\]

може бути переписаний як вираз явно за участю$n$, наприклад$32/3(1-1/n^2)$.

Розглядаючи таким чином, ми можемо думати про підсумовування як функцію$n$. Задано$n$ значення (де$n$ є додатним цілим числом) і повертається сума площ$n$ рівновіддалених прямокутників за допомогою Правил Лівої руки, Правої руки або Середньої точки.

З огляду на певний інтеграл$\int_a^b f(x)dx$, нехай:

1. $S_L(n) = \sum_{i=1}^n f(x_i)\Delta x$, сума рівновіддалених прямокутників, утворених за допомогою правила Лівої руки,
2. $S_R(n) = \sum_{i=1}^n f(x_{i+1})\Delta x$, сума рівновіддалених прямокутників, утворених за допомогою Правил правої руки, і
3. $S_M(n) = \sum_{i=1}^n f\left(\frac{x_i+x_{i+1}}{2}\right)\Delta x$, сума однаково розташованих прямокутників, утворених за допомогою правила середньої точки.

Згадаймо визначення межі як$n\to\infty$:$\lim_{n\to\infty}S_L(n) = K$ якщо, з огляду на будь-який$\epsilon>0$, існує$N>0$ таке, що

$$\ left|s_l (n) -K\ праворуч | <\ epsilon\ quad\ text {коли}\ quad n\ geq N\]

Наступна теорема стверджує, що ми можемо використовувати будь-яке з наших трьох правил, щоб знайти точне значення певного інтеграла$\int_a^b f(x)dx$. Це також йде на два кроки далі. Теорема стверджує, що висоту кожного прямокутника не потрібно визначати за певним правилом, але може бути$f(c_i)$, де$c_i$ знаходиться будь-яка точка в$i^\text{ th}$ підінтервалі, як обговорювалося раніше Суми Рімана, де визначено у визначенні$\PageIndex{1}$.

Теорема продовжує стверджувати, що прямокутники не повинні бути однакової ширини. Використовуючи позначення Definition$\PageIndex{1}$, давайте$\Delta x_i$ позначимо довжину$i^\text{ th}$ підінтервалу в розділі$[a,b]$. Тепер давайте$||\Delta x||$ представляємо довжину найбільшого підінтервалу в розділі: тобто є найбільшим з усіх. Якщо$||\Delta x||$ маленький, то$[a,b]$ повинні бути розділені на багато підінтервалів, оскільки всі підінтервали повинні мати невелику довжину.$||\Delta x||$$\Delta x_i$ «Прийняття межі як$||\Delta x||$ йде до нуля» означає, що$n$ кількість субінтервалів у розділі зростає до нескінченності, оскільки найбільша підінтервальна довжина стає довільно малою. Потім ми інтерпретуємо вираз

$\ lim_ {||\ Дельта x||\ до 0}\ sum_ {i=1} ^nf (c_i)\ Дельта x_i\]

як «межа суми прямокутників, де ширина кожного прямокутника може бути різною, але стає маленькою, і висота кожного прямокутника не обов'язково визначається певним правилом». Теорема стверджує, що ця сума Рімана також дає значення певного інтеграла$f$ понад$[a,b]$.

Теорема$\PageIndex{2}$: Definite Integrals and the Limit of Riemann Sums

$f$Дозволяти бути безперервним на замкнутому інтервалі$[a,b]$ і нехай$S_L(n)$,$S_R(n)$ і$S_M(n)$ бути визначені як раніше. Потім:

1. $\lim_{n\to\infty} S_L(n) = \lim_{n\to\infty} S_R(n) = \lim_{n\to\infty} S_M(n) = \lim_{n\to\infty}\sum_{i=1}^n f(c_i)\Delta x$,
2. $\lim_{n\to\infty}\sum_{i=1}^n f(c_i)\Delta x = \int_a^b f(x)dx$, and %$ \lim_{n\to\infty} S_L(n) = \int_a^b f(x)dx$.
3. $\lim_{\|\Delta x\|\to 0} \sum_{i=1}^n f(c_i)\Delta x_i = \int_a^b f(x)dx$.

Ми підсумовуємо те, що ми дізналися за останні кілька розділів тут.

• Знання «площі під кривою» може бути корисним. Одним із поширених прикладів є: площа під кривою швидкості є зміщенням.
• Ми визначили певний інтеграл$\int_a^b f(x)dx$, який буде знаковою областю під$f$ інтервалом$[a,b]$.
• Хоча ми можемо наблизити певний інтеграл багатьма способами, ми зосередилися на використанні прямокутників, висоту яких можна визначити за допомогою: Правило лівої руки, Правило правої руки та Правило середньої точки.
• Суми прямокутників цього типу називаються сумами Рімана.
• Точне значення визначеного інтеграла можна обчислити за допомогою межі суми Рімана. Зазвичай ми використовуємо один із зазначених вище методів, оскільки він робить алгебру простішою.

Спочатку ми дізналися про похідні через обмеження, потім вивчили правила, які спростили процес. Ми знаємо спосіб оцінити певний інтеграл, використовуючи межі; у наступному розділі ми побачимо, як фундаментальна теорема обчислення робить процес простішим. Ключовою особливістю цієї теореми є її зв'язок між невизначеною інтегралом і певним інтегралом.

Дописувачі та атрибуція

• Template:ContribApexCalc
• Template:ContribMarshall