5.5: Чисельна інтеграція
- Page ID
- 60716
Фундаментальна теорема обчислення дає конкретну методику знаходження точного значення певного інтеграла. Ця методика заснована на обчисленні антипохідних. Незважаючи на силу цієї теореми, все ж існують ситуації, коли ми повинні наблизити значення певного інтеграла замість того, щоб знайти його точне значення. Перша ситуація, яку ми досліджуємо, полягає в тому, що ми не можемо обчислити антипохідне цілого. Другий випадок, коли ми насправді не знаємо цілісного, а тільки його значення при оцінці в певних точках.
Елементарна функція - це будь-яка функція, яка являє собою комбінацію поліномів,\(n^{\text{th}}\) коренів, раціональних, експоненціальних, логарифмічних і тригонометричних функцій. Ми можемо обчислити похідну будь-якої елементарної функції, але є багато елементарних функцій, з яких ми не можемо обчислити антидериватив. Наприклад, такі функції не мають антипохідних, які ми можемо висловити елементарними функціями:
$ $ e^ {-x^2},\ квад\ sin (x^3)\ квад\ текст {і}\ квад\ розрив {\ sin x} {x}.\]
Найпростіший спосіб звернутися до антипохідних\(e^{-x^2}\) - це просто написати\(\int e^{-x^2}\ dx\).
У цьому розділі окреслено три загальні методи наближення значення визначених інтегралів. Кожен з них описується як систематичний метод апроксимації площі під кривою. Апроксимуючи цю область точно, ми знаходимо точне наближення відповідного певного інтеграла.
Ми будемо застосовувати методи, які ми вивчаємо в цьому розділі, до наступних визначених інтегралів:
$\ int_0^1 e^ {-x^2}\ dx,\ quad\ int_ {-\ frac {\ pi} {4}} ^ {\ frac {\ pi} {2}}\ sin (x^3)\ dx,\ квад\ текст {і}\ quad\ int_ {0.5} ^ {4\ pi}\ frac {\ sin (x)} {x}\ dx,\]
як зображено на малюнку\(\PageIndex{1}\).
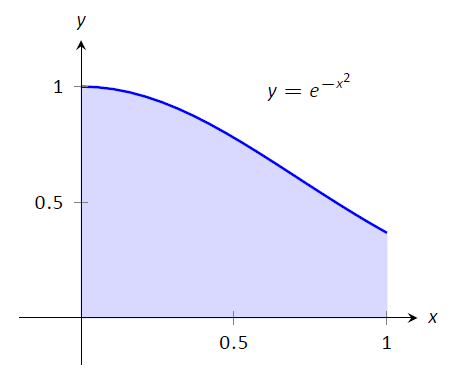
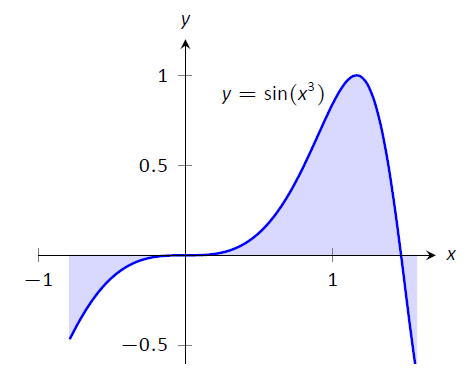
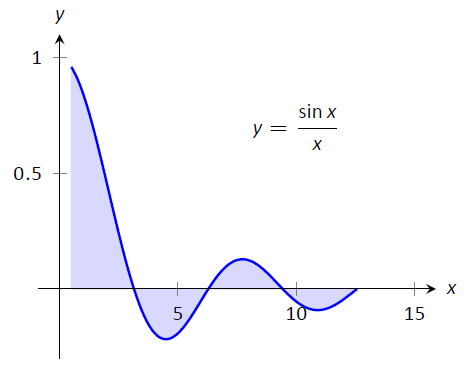
Малюнок\(\PageIndex{1}\): Графічно представляють три визначені інтеграли, які не можуть бути оцінені за допомогою антипохідних.
Методи правила лівої та правої руки
У розділі 5.3 ми розглянули задачу оцінки визначених інтегралів шляхом наближення площі під кривою за допомогою прямокутників. Ми переглядаємо ці ідеї тут, перш ніж вводити інші методи наближення певних інтегралів.
Почнемо з огляду позначень. \(f\)Дозволяти бути безперервна функція на інтервалі\([a,b]\). Бажаємо наблизити\(\int_a^b f(x)\ dx\). \([a,b]\)Розбиваємо на\(n\) однаково розташовані підінтервали, кожен довжини\(dx = \frac{b-a}{n}\). Кінцеві точки цих підінтервалів позначені як
$ х_1=а,\ x_2 = а+дх,\ x_3 = a+ 2dx,\\ ldpots,\ x_i = a+ (i-1)\ dx,\\ ldpots,\ x_ {n+1} = б.\]
Ключова ідея 8 стверджує, що для використання правила лівої руки ми використовуємо підсумовування\( \sum_{i=1}^n f(x_i)\ dx\) і використовувати правило правої руки, яке ми використовуємо\( \sum_{i=1}^n f(x_{i+1})\ dx\). Ми розглядаємо використання цих правил в контексті прикладів.
Приклад\(\PageIndex{1}\): Approximating definite integrals with rectangles
Наближене\( \int_0^1e^{-x^2}\ dx\) використання правил лівої та правої руки з 5 однаково розташованими підінтервалами.
Рішення
Починаємо з поділу інтервалу\([0,1]\) на 5 однаково розташованих інтервалів. У нас є\(dx = \frac{1-0}5 = 1/5=0.2\), так $x_1 = 0,\ x_2 = 0,2,\ x_3 = 0,4,\ x_4 = 0,6,\ x_5 = 0,8,\\ текст {і}\ x_6 = 1.\]
Використовуючи правило лівої руки, ми маємо:
\[\begin{align} \sum_{i=1}^n f(x_i)\ dx &= \big(f(x_1)+f(x_2) + f(x_3) + f(x_4) + f(x_5)\big)\ dx \\ &= \big(f(0) + f(0.2) + f(0.4) + f(0.6) + f(0.8)\big)\ dx \\ &\approx \big(1+0.961 + 0.852 + 0.698 + 0.527)(0.2)\\ &\approx 0.808.\end{align}\]
Використовуючи правило правої руки, ми маємо:
\ [\ почати {вирівняти}\ сума_ {i = 1} ^n f (x_ {i+1})\ dx &=\ великий (f (x_2) + f (x_3) + f (x_4) + f (x_5) +f (x_6)\ великий)\ dx\\ &=\ великий (f (0.2) + f (0.4) + f (0.4) + f (0.6) + f (0.6) + f (0.6) + f (0.6) + f (0,8) +f (1)\ великий)\ dx\\ &\ приблизно\ великий (0,961 +0,852 + 0,698 + 0,527 + 0,368) (0,2)\\\ &\ приблизно 0,681.
\ end {вирівняти}\]
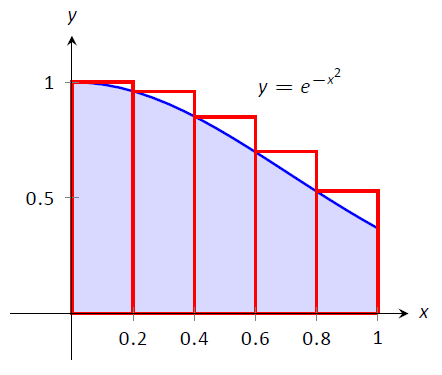
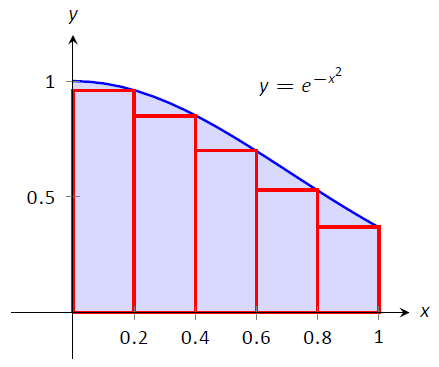
Малюнок\(\PageIndex{2}\): Апроксимація\(\int_0^1e^{-x^2}\ dx\) в прикладі\(\PageIndex{1}\)
\(\PageIndex{2}\)На малюнку показані прямокутники, які використовуються в кожному методі для наближення певного інтеграла. Ці графіки показують, що в даному конкретному випадку правило лівої руки є надмірним наближенням, а Правило правої руки - під наближенням. Щоб отримати краще наближення, ми могли б використовувати більше прямокутників, як ми це робили в розділі 3.1. Ми також могли б усереднити результати правила лівої та правої руки разом, даючи
$$\ гідророзриву {0.808 + 0.681} {2} = 0.7445.\]
Фактична відповідь, з точністю до 4 знаків після десяткового дробу, становить 0.7468, показуючи наше середнє значення є хорошим наближенням.
Приклад\(\PageIndex{2}\): Approximating definite integrals with rectangles
Наближене\(\int_{-\frac{\pi}4}^{\frac{\pi}2} \sin (x^3)\ dx\) використання правил лівої та правої руки з 10 однаково розташованими підінтервалами.
Рішення
Почнемо з знаходження\ Delta x:
$\ розрив {b-a} {n} =\ гідророзриву {\ pi/2 - (-\ pi/4)} {10} =\ гідророзриву {3\ pi} {40}\ приблизно 0,236.\]
Корисно виписати кінцеві точки підінтервалів в таблицю; в таблиці\(\PageIndex{1}\) ми наведемо точні значення кінцевих точок, їх десяткові наближення та десяткові наближення\(\sin(x^3)\) обчислюваних в цих точках.
| \(x_i\) | Точний | Прибл. | \(\sin(x_i^3)\) |
|---|---|---|---|
| \ (x_i\) ">\(x_1\) | \(-\pi/4\) | \(-0.785\) | \ (\ sin (x_i^3)\) ">\(-0.466\) |
| \ (x_i\) ">\(x_2\) | \(-7 \pi/40\) | \(-0.550\) | \ (\ sin (x_i^3)\) ">\(-0.165\) |
| \ (x_i\) ">\(x_3\) | \(-{\pi }/{10}\) | \(-0.314\) | \ (\ sin (x_i^3)\) ">\(-0.031\) |
| \ (x_i\) ">\(x_4\) | \(-{\pi }/{40}\) | \(-0.0785\) | \ (\ sin (x_i^3)\) ">\(0\) |
| \ (x_i\) ">\(x_5\) | \({\pi }/{20}\) | 0.157 | \ (\ sin (x_i^3)\) ">0.004 |
| \ (x_i\) ">\(x_6\) | \({\pi }/{8}\) | 0,393 | \ (\ sin (x_i^3)\) ">0.061 |
| \ (x_i\) ">\(x_7\) | \({\pi }/{5}\) | 0,628 | \ (\ sin (x_i^3)\) ">0.246 |
| \ (x_i\) ">\(x_8\) | \({11 \pi }/{40}\) | 0,864 | \ (\ sin (x_i^3)\) ">0.601 |
| \ (x_i\) ">\(x_9\) | \({7 \pi }/{20}\) | 1.10 | \ (\ sin (x_i^3)\) ">0.971 |
| \ (x_i\) ">\(x_{10}\) | \({17 \pi }/{40}\) | 1.34 | \ (\ sin (x_i^3)\) ">0.690 |
| \ (x_i\) ">\(x_{11}\) | \({\pi}/{2}\) | 1.57 | \ (\ sin (x_i^3)\) ">\(-0.670\) |
Після створення цієї таблиці можна просто наблизити певний інтеграл за допомогою Правил лівої та правої руки. (Примітка: саму таблицю легко створити, особливо зі стандартною програмою електронних таблиць на комп'ютері. Останні дві колонки - це все, що потрібно.) Правило лівої руки підсумовує перші 10 значень\(\sin(x_i^3)\) і множить суму на\(dx\); Правило правої руки підсумовує останні 10 значень\(\sin(x_i^3)\) і множить на\(dx\). Тому у нас є:
Правило лівої руки:\(\int_{-\frac{\pi}4}^{\frac{\pi}2}\sin(x^3)\ dx \approx (1.91)(0.236) = 0.451.\)
Правило правої руки:\(\int_{-\frac{\pi}4}^{\frac{\pi}2}\sin(x^3)\ dx \approx (1.71)(0.236) = 0.404.\)
Середнє значення правил лівої та правої руки: 0.4275.
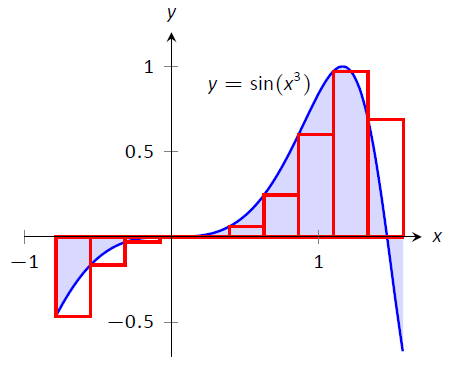
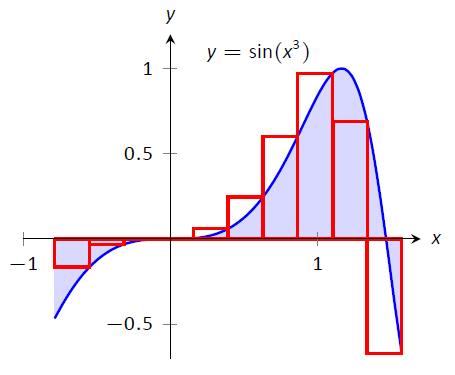
Малюнок\(\PageIndex{3}\):\(\int_{-\frac{\pi}4}^{\frac{\pi}2}\sin(x^3)\ dx\) у прикладі\(\PageIndex{2}\)
Фактична відповідь, з точністю до 3 знаків після десяткового дробу, дорівнює 0,460. Наші наближення знову були досить хорошими. Прямокутники, використані в кожному наближенні, наведені на малюнку\(\PageIndex{3}\). З графіків зрозуміло, що використання більшої кількості прямокутників (а значить, і більш вузьких прямокутників) повинно привести до більш точного наближення.
Трапецієподібне правило
У прикладі\(\PageIndex{1}\) ми наблизили значення\(\int_0^1 e^{-x^2}\ dx\) з 5 прямокутників однакової ширини. \(\PageIndex{2}\)На малюнку показані прямокутники, які використовуються в правилах лівої та правої руки. Ці графіки чітко показують, що прямокутники не так добре відповідають формі графіка, і що точні наближення прийдуть лише за допомогою безлічі прямокутників.
Замість того, щоб використовувати прямокутники для наближення площі, ми можемо замість цього використовувати трапеції. На малюнку\(\PageIndex{4}\) ми показуємо область під\(f(x) = e^{-x^2}\) на\([0,1]\) наближену 5 трапеціями однакової ширини; верхні «кути» кожної трапеції лежать на графіку\(f(x)\). З цієї цифри зрозуміло, що ці трапеції більш точно наближають площу під\(f\) і, отже, повинні давати краще наближення\(\int_0^1 e^{-x^2}\ dx\). (Насправді ці трапеції, здається, дають велике наближення площі!)
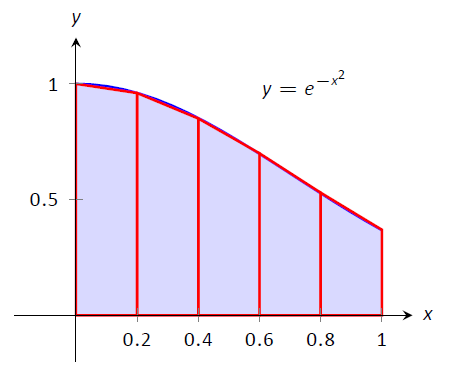
Малюнок\(\PageIndex{4}\): Апроксимація\(\int_0^1 e^{-x^2}\ dx\) за допомогою 5 трапецій однакової ширини.
Формула для площі трапеції наведена на малюнку\(\PageIndex{5}\). Ми\(\int_0^1 e^{-x^2}\ dx\) наближаємо з цими трапеціями в наступному прикладі.
Приклад\(\PageIndex{3}\): Approximating definite integrals using trapezoids
Використовуйте 5 трапецій однакової ширини для наближення\(\int_0^1e^{-x^2}\ dx\).
Рішення
Для обчислення площ 5 трапецій на малюнку знову буде корисно створити таблицю значень\(\PageIndex{6}\), як показано в табл\(\PageIndex{2}\).
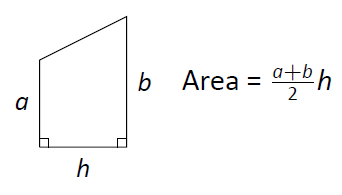
Малюнок\(\PageIndex{5}\): Площа трапеції
| \(x_i\) | \(e^{-x_i^2}\) |
|---|---|
| \ (x_i\) ">0 | \ (e^ {-x_i^2}\) ">1 |
| \ (x_i\) ">0.2 | \ (e^ {-x_i^2}\) ">0.961 |
| \ (x_i\) ">0.4 | \ (e^ {-x_i^2}\) ">0.852 |
| \ (x_i\) ">0.6 | \ (e^ {-x_i^2}\) ">0.698 |
| \ (x_i\) ">0.8 | \ (e^ {-x_i^2}\) ">0.527 |
| \ (x_i\) ">1 | \ (e^ {-x_i^2}\) ">0.368 |
Крайня ліва трапеція має ніжки довжиною 1 і 0,961 і висотою 0,2. Таким чином, за нашою формулою площа крайньої лівої трапеції дорівнює:
$\ гідророзриву {1+0.961} {2} (0.2) = 0.1961.\]
Рухаючись вправо, наступна трапеція має ноги довжиною 0,961 і 0,852 і висотою 0,2. Таким чином, його площа становить:
$\ гідророзриву {0.961+0.852} 2 (0,2) = 0.1813.\]
Сума площ всіх 5 трапецій становить:
\[\begin{align} \frac{1+0.961}{2}(0.2) + \frac{0.961+0.852}2(0.2)+\frac{0.852+0.698}2(0.2)&+ \\ \frac{0.698+0.527}2(0.2)+\frac{0.527+0.368}2(0.2)&= 0.7445. \end{align}\]
Ми наближаємо\(\int_0^1 e^{-x^2}\ dx \approx 0.7445.\)
У цьому прикладі можна спостерігати багато речей. Зверніть увагу, як кожен член в остаточному підсумовуванні множився як на 1/2, так і на\(dx = 0.2\). Ми можемо врахувати ці коефіцієнти, залишивши більш стисле підсумовування як:
$\ фрак12 (0.2)\ великий [(1+0.961) + (0.961+0.852) + (0.852+0.698) + (0.698+ 0,527) + (0.527 + 0,368)\ Великий].\]
Тепер зверніть увагу, що всі числа, крім першого і останнього, додаються двічі. Тому ми можемо написати підсумовування ще більш лаконічно, як
$\ гідророзрив {0.2} {2}\ Великий [1 + 2 (0.961+0.852+0.698+0.527) + 0,368\ Великий].\]
Це серце трапецієподібного правила, де певний інтеграл\(\int_a^b f(x) \ dx\) наближається за допомогою трапецій рівної ширини для наближення відповідної площі під\(f\). Використовуючи\(n\) однаково розташовані підінтервали з кінцевими точками\(x_1\)\(x_2\),\(\ldots\),\(x_{n+1}\),, ми знову маємо\( \Delta x = \frac{b-a}n\). Таким чином:
\[\begin{align} \int_a^b f(x)\ dx & \approx \sum_{i=1}^n \frac{f(x_i)+f(x_{i+1})}2\ dx \\ & = \frac{\ dx}2 \sum_{i=1}^n \big(f(x_i)+f(x_{i+1})\big)\\ & = \frac{\ dx}2\Big[f(x_1)+ 2\sum_{i=2}^n f(x_i) + f(x_{n+1})\Big].\end{align}\]
Приклад\(\PageIndex{4}\): Using the Trapezoidal Rule
Перегляньте приклад\(\PageIndex{4}\) та наблизитесь\(\int_{-\frac{\pi}{4}}^{\frac{\pi}{2}} \sin (x^3)\ dx\) за допомогою трапецієподібного правила та 10 однаково розташованих підінтервалів.
Рішення
Повертаємося до Таблиці\(\PageIndex{1}\) для таблиці значень\(\sin(x^3)\). Нагадаємо, що\(dx = 3\pi/40 \approx 0.236\). Таким чином, ми маємо:
\[\begin{align*}\int_{-\frac {\pi}4}^{\frac{\pi}2} \sin (x^3)\ dx &\approx \frac{0.236}{2}\Big[-0.466 + 2\Big(-0.165+(-0.031)+\ldots+0.69\Big)+(-0.67)\Big]\\ &= 0.4275. \end{align*}\]
Зверніть увагу, як «швидко» трапецієподібне правило може бути реалізовано після створення таблиці значень. Це справедливо для всіх методів, досліджених у цьому розділі; реальною роботою є створення таблиці\(x_i\) та\(f(x_i)\) значень. Як тільки це буде завершено, наблизити певний інтеграл не складе труднощів. Знову ж таки, використовувати технологію розумно. Електронні таблиці можуть зробити швидку роботу цих обчислень і полегшити використання безлічі субінтервалів.
Також зверніть увагу на наближення, які дає трапецієподібне правило. Це середнє значення наближень, заданих Правилами лівої та Правої Руки! Це ефективно робить правила лівої та правої руки застарілими. Вони корисні при першому вивченні певних інтегралів, але якщо потрібне реальне наближення, то, як правило, краще використовувати трапецієподібне правило замість правила лівої або правої руки.
Як ми можемо вдосконалити трапецієподібне правило, окрім використання все більшої кількості трапецій? Відповідь зрозуміла, як тільки ми озирнемося назад і розглянемо, що ми насправді зробили досі. Правило лівої руки насправді не стосується використання прямокутників для наближення площі. Натомість він наближає функцію\(f\) з постійними функціями на малих підінтервалах, а потім обчислює певний інтеграл цих постійних функцій. Трапецієподібне правило дійсно апроксимує функцію\(f\) з лінійною функцією на малому підінтервалі, потім обчислює певний інтеграл цієї лінійної функції. В обох цих випадках певні інтеграли легко обчислити в геометричному вираженні.
Отже, ми маємо прогресію: ми починаємо з наближення\(f\) з постійною функцією, а потім з лінійною функцією. Що далі? Квадратична функція. Апроксимуючи криву функції з безліччю парабол, ми, як правило, отримуємо ще краще наближення певного інтеграла. Ми називаємо цей процес Правилом Сімпсона, названим на честь Томаса Сімпсона (1710-1761), хоча інші використовували це правило аж 100 років до цього.
Правило Сімпсона
З огляду на один момент, ми можемо створити постійну функцію, яка проходить через цю точку. З огляду на дві точки, ми можемо створити лінійну функцію, яка проходить через ці точки. Враховуючи три точки, ми можемо створити квадратичну функцію, яка проходить через ці три точки (враховуючи, що жодна з двох не має однакового\(x\) —value).
Розглянемо три точки\((x_1,y_1)\),\((x_2,y_2)\) і\((x_3,y_3)\) чиї\(x\) —значення однаково розташовані і\(x_1<x_2<x_3\). \(f\)Дозволяти квадратичної функції, яка проходить через ці три точки. Це не важко показати, що
\[\int_{x_1}^{x_3} f(x)\ dx = \frac{x_3-x_1}{6}\big(y_1+4y_2+y_3\big).\]
Розглянемо Малюнок\(\PageIndex{6}\). Функція\(f\) проходить через показані 3 точки, а парабола\(g\), яка також проходить через ці точки, графічна пунктирною лінією. Використовуючи наше рівняння зверху, ми точно знаємо, що $$\ int_1^3 g (x)\ dx =\ frac {3-1} {6}\ big (3+4 (1) +2\ big) = 3.$$ Оскільки\(g\) є хорошим наближенням для\(f\) включення\([1,3]\), ми можемо констатувати, що $$\ int_1^3 f (x)\ dx\ приблизно 3.
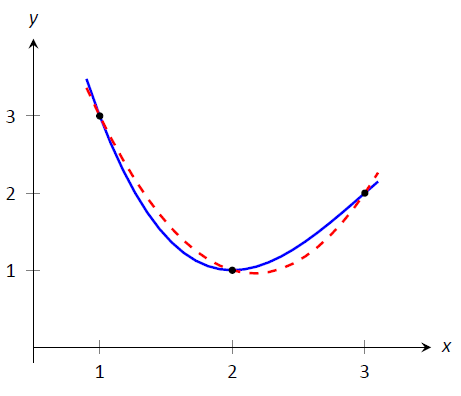
Малюнок\(\PageIndex{6}\): Графік функції\(f\) та параболи, яка добре її наближає\([1,3]\).
Зверніть увагу, як інтервал\([1,3]\) був розділений на два підінтервали, оскільки нам потрібно було 3 бали. Через це, всякий раз, коли ми використовуємо Правило Сімпсона, нам потрібно розбити інтервал на парну кількість підінтервалів.
Загалом, щоб наблизити\(\int_a^b f(x)\ dx\) за допомогою Правила Сімпсона,\([a,b]\) поділіть на\(n\) підінтервали, де\(n\) парний і кожен підінтервал має ширину\(\ dx = (b-a)/n\). Ми\(f\) наближаємося\(n/2\) параболічними кривими, використовуючи Рівняння\(\PageIndex{22}\) для обчислення площі під цими параболами. Складання цих областей дає формулу:
$\ int_a^b f (x)\ dx\ приблизно\ розрив {\ dx} 3\ великий [f (x_1) +4f (x_2) +2f (x_3) +4f (x_4) +\ ldots+2f (x_ {n-1}) +4f (x_n) +f (x_ {n+1})\ великий]\.]
Зверніть увагу, як коефіцієнти членів при підсумовуванні мають візерунок 1, 4, 2, 4, 2, 4\(\ldots\), 2, 4, 1.
Давайте продемонструємо Правило Сімпсона на конкретному прикладі.
Приклад\(\PageIndex{5}\): Using Simpson's Rule
Приблизно\(\int_0^1 e^{-x^2}\ dx\) за допомогою правила Сімпсона та 4 однаково розташованих підінтервалів.
Рішення
Ми починаємо з складання таблиці значень, як ми мали в минулому, як показано в табл\(\PageIndex{3}\).
| \(x_i\) | \(e^{-x_i^2}\) |
|---|---|
| \ (x_i\) ">0 | \ (e^ {-x_i^2}\) ">1 |
| \ (x_i\) ">0,25 | \ (e^ {-x_i^2}\) ">0.939 |
| \ (x_i\) ">0.5 | \ (e^ {-x_i^2}\) ">0.779 |
| \ (x_i\) ">0,75 | \ (e^ {-x_i^2}\) ">0.570 |
| \ (x_i\) ">1 | \ (e^ {-x_i^2}\) ">0.368 |
Правило Сімпсона стверджує, що
$\ int_0^1e^ {-x^2}\ dx\ приблизно\ розрив {0,25} {3}\ Великий [1+4 (0.939) +2 (0.779) +4 (0.570) + 0,368\ Великий] = 0.7468\ overline {3}.\]
Нагадаємо, в прикладі\(\PageIndex{1}\) ми заявили, що правильна відповідь, з точністю до 4 знаків після десяткового дробу, склала 0.7468. Наше наближення з правилом Сімпсона, з 4 підінтервалами, краще, ніж наше наближення з трапецієподібним правилом, використовуючи 5!
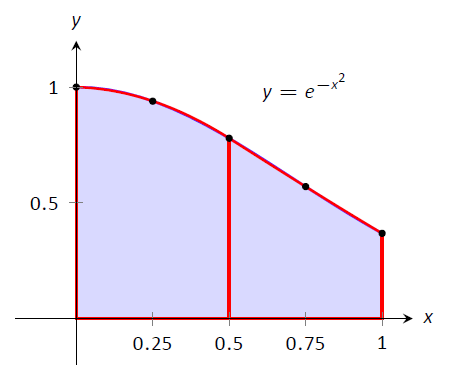
Малюнок\(\PageIndex{7}\): Використання правила Сімпсона з\(n=4\) для наближення\(\int_0^1 e^{-x^2}\ dx\).
Малюнок\(\PageIndex{7}\) показує\(f(x) = e^{-x^2}\) разом зі своїми апроксимуючими параболами, демонструючи, наскільки добре наше наближення. Апроксимуючі криві майже не відрізняються від фактичної функції.
Приклад\(\PageIndex{6}\): Using Simpson's Rule
Приблизно\(\int_{-\frac{\pi}4}^{\frac{\pi}2} \sin (x^3)\ dx\) за допомогою правила Сімпсона та 10 однаково розставлених інтервалів.
Рішення
Таблиця\(\PageIndex{4}\) показує таблицю значень, які ми використовували в минулому для цієї проблеми, показана тут знову для зручності. Знову ж таки,\(\ dx = (\pi/2+\pi/4)/10 \approx 0.236\).
| \(x_i\) | \(\sin(x_i^3)\) |
|---|---|
| \ (x_i\) ">\(-0.785\) | \ (\ sin (x_i^3)\) ">\(-0.466\) |
| \ (x_i\) ">\(-0.550\) | \ (\ sin (x_i^3)\) ">\(-0.165\) |
| \ (x_i\) ">\(-0.314\) | \ (\ sin (x_i^3)\) ">\(-0.031\) |
| \ (x_i\) ">\(-0.0785\) | \ (\ sin (x_i^3)\) ">\(0\) |
| \ (x_i\) ">0.157 | \ (\ sin (x_i^3)\) ">0.004 |
| \ (x_i\) ">0,393 | \ (\ sin (x_i^3)\) ">0.061 |
| \ (x_i\) ">0.628 | \ (\ sin (x_i^3)\) ">0.246 |
| \ (x_i\) ">0.864 | \ (\ sin (x_i^3)\) ">0.601 |
| \ (x_i\) ">1.10 | \ (\ sin (x_i^3)\) ">0.971 |
| \ (x_i\) ">1.34 | \ (\ sin (x_i^3)\) ">0.690 |
| \ (x_i\) ">1.57 | \ (\ sin (x_i^3)\) ">\(-0.670\) |
Правило Сімпсона стверджує, що
\[\begin{align}\int_{-\frac{\pi}4}^{\frac{\pi}2} \sin (x^3)\ dx &\approx \frac{0.236}3\Big[(-0.466)+4(-0.165)+2(-0.031) + \ldots \\ & \ldots + 2(0.971) + 4(0.69) + (-0.67)\big]\\ &= 0.4701\end{align}\]
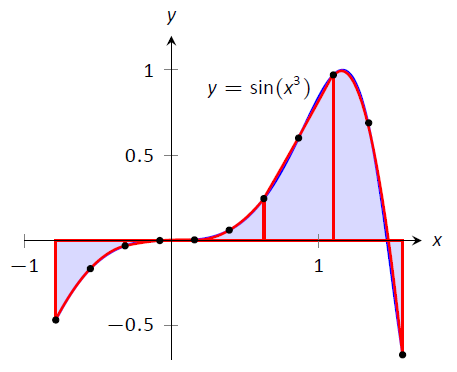
Малюнок\(\PageIndex{8}\): Наближення\(\int_{-\frac{\pi}4}^{\frac{\pi}2}\sin(x^3)\ dx\) у прикладі\(\PageIndex{6}\) з правилом Сімпсона та 10 однаково розташованими інтервалами.
Нагадаємо, що фактичне значення, з точністю до 3 знаків після коми, дорівнює 0,460. Наше наближення знаходиться в межах однієї 1/100\(^\text{th}\) від правильного значення. Графік на малюнку\(\PageIndex{8}\) показує, наскільки точно параболи відповідають формі графіка.
Резюме та аналіз помилок
Ми узагальнюємо ключові поняття цього розділу на сьогоднішній день у наступній Key Idea.
Ключова ідея 9: Чисельне інтегрування
\(f\)Дозволяти бути безперервна функція на\([a,b]\), нехай\(n\) буде натуральне число, і нехай\(\Delta x = \frac{b-a}{n}\).
Набір\(x_1=a\),\(x_2 = a+\ dx\),\(\ldots\),\(x_i = a+(i-1)\ dx\),\(x_{n+1}=b\).
Розглянемо\(\int_a^b f(x)\ dx\).
Правило лівої руки:\(\int_a^b f(x)\ dx \approx \ dx\Big[f(x_1) + f(x_2) + \ldots + f(x_n)\big]\).
Правило правої руки:\(\int_a^b f(x)\ dx \approx \ dx\Big[f(x_2) + f(x_3) + \ldots + f(x_{n+1})\big]\).
Трапецієподібне правило:\(\int_a^b f(x)\ dx \approx \frac{\ dx}2\Big[f(x_1) + 2f(x_2) + 2f(x_3) +\ldots + 2f(x_n)+ f(x_{n+1})\big]\).
Правило Сімпсона:\(\int_a^b f(x)\ dx \approx \frac{\ dx}3\Big[f(x_1) + 4f(x_2) + 2f(x_3) +\ldots + 4f(x_n)+ f(x_{n+1})\big]\) (\(n\)парне)}.
У наших прикладах ми наблизили значення певного інтеграла за допомогою заданого методу, а потім порівняли його з «правильною» відповіддю. Це повинно було викликати кілька питань у свідомості читача, таких як:
- Як обчислювалася «правильна» відповідь?
- Якщо вдасться знайти правильну відповідь, який сенс наближення?
- Якщо є значення для наближення, як ми повинні знати, чи є наближення будь-яким хорошим?
Це хороші питання, і відповіді на них навчальні. У прикладах правильну відповідь так і не обчислювався. Швидше за все, було дано наближення з точністю до певної кількості знаків після десяткового числа. У прикладі\(\PageIndex{1}\) ми не знаємо точної відповіді, але ми знаємо, що вона починається з 0.7468. Ці більш точні наближення обчислювалися за допомогою числового інтегрування, але з більшою точністю (тобто більше субінтервалів та допомогою комп'ютера).
Оскільки точної відповіді знайти не вдається, наближення все ще має своє місце. Як ми можемо визначити, чи є наближення будь-яким хорошим?
«Проби і помилки» передбачає один спосіб. Використовуючи технологію, зробіть наближення з, скажімо, 10, 100 і 200 субінтервалами. Це, швидше за все, не займе багато часу, і повинна з'явитися тенденція. Якщо тенденція не виникає, спробуйте використовувати ще більше субінтервалів. Майте на увазі, що спроби та помилки ніколи не є безглуздими; ви можете наштовхнутися на проблему, в якій тенденція не з'явиться.
Другий спосіб полягає у використанні аналізу помилок. Хоча деталі виходять за рамки цього тексту, є деякі формули, які дають межі того, наскільки добре буде ваше наближення. Наприклад, формула може стверджувати, що наближення знаходиться в межах 0,1 від правильної відповіді. Якщо наближення дорівнює 1,58, то відомо, що правильна відповідь знаходиться між 1,48 і 1,68. Використовуючи безліч підінтервалів, можна отримати наближення настільки точно, як подобається. Теорема\(\PageIndex{1}\) стверджує, що це за межі.
Теорема\(\PageIndex{1}\): Error Bounds in the Trapezoidal and Simpson's Rules
- \(E_T\)Дозволяти помилка в наближенні за\( \int_a^b f(x)\ dx\) допомогою трапецієподібного правила.
Якщо\(f\) має безперервну\(^\text{nd}\) похідну 2 на\([a,b]\) і\(M\) є будь-якою верхньою межею\(\big|f"(x)\big|\) on\([a,b]\), то
$$ E_T\ лек\ гідророзриву {(b-a) ^3} {12n^2} М.\]
- \(E_S\)Дозволяти бути помилкою в наближенні\( \int_a^b f(x)\ dx\) за допомогою правила Сімпсона.
Якщо\(f\) має безперервну\(^\text{th}\) похідну 4 на\([a,b]\) і\(M\) є будь-якою верхньою межею\(\big|f\,^{(4)}\big|\) on\([a,b]\), то
$E_S\ лек\ гідророзриву {(б-а) ^5} {180n^4} М.\]
Є деякі ключові речі, які слід зазначити щодо цієї теореми.
- Чим більше інтервал, тим більше похибка. Це повинно мати сенс інтуїтивно.
- Помилка зменшується, оскільки використовується більше субінтервалів (тобто, як\(n\) стає більшим).
- Помилка в Правилі Сімпсона має термін, що відноситься до 4\(^{\text{th}}\) похідної від\(f\). Розглянемо кубічний многочлен: його\(4^{\text{th}}\) похідна дорівнює 0. Отже, похибка наближення певного інтеграла кубічного полінома правилом Сімпсона дорівнює 0 — Правило Сімпсона обчислює точну відповідь!
Ми переглядаємо Приклади\(\PageIndex{3}\)\(\PageIndex{5}\) та обчислюємо межі помилок, використовуючи теорему\(\PageIndex{1}\) в наступному прикладі.
Приклад\(\PageIndex{7}\): Computing error bounds
Знайдіть межі помилок під час апроксимації\( \int_0^1 e^{-x^2}\ dx\) за допомогою трапецієподібного правила та 5 підінтервалів та використання правила Сімпсона з 4 підінтервалами.
Рішення
Трапецієподібне правило з\(n=5\):
Почнемо з обчислення\(2^\text{nd}\) похідної від\(f(x) = e^{-x^2}\):
\[f"(x) = e^{-x^2}(4x^2-2).\]
\(\PageIndex{8}\)На малюнку зображений графік\(f"(x)\) включення\([0,1]\). Зрозуміло, що найбільше значення\(f"\), в абсолютному значенні, дорівнює 2. Таким чином, ми дозволяємо\(M=2\) і застосовуємо формулу помилки з теореми\(\PageIndex{1}\).
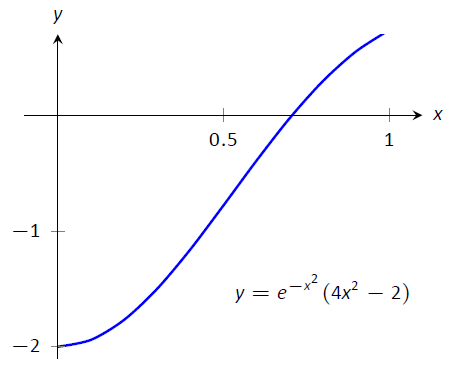
Малюнок\(\PageIndex{9}\): Графік\(f"(x)\) у прикладі,\(\PageIndex{7}\) щоб допомогти встановити межі помилок.
$ $ E_T =\ frac {(1-0) ^3} {12\ cdot 5 ^ 2}\ cdot 2 = 0.00\ оверлайн {6}.\]
Наша формула оцінки помилок стверджує, що наше наближення 0.7445, знайдене в прикладі,\(\PageIndex{3}\) знаходиться в межах 0,0067 від правильної відповіді, отже, ми знаємо, що
$0,7445-0,0067 = .7378\ leq\ int_0^1e^ {-x^2}\ dx\ лек 0.7512 = 0.7445 + 0,0067.\]
Раніше ми обчислювали точну відповідь, правильну до 4 знаків після коми, щоб бути 0.7468, підтверджуючи дійсність теореми\(\PageIndex{1}\).
Правило Сімпсона з\(n=4\):
Почнемо з обчислення\(4^\text{th}\) похідної від\(f(x) = e^{-x^2}\):
$ $ ф\, ^ {(4)} (х) = e^ {-х^2} (16х^4-48х^2+12).\]
\(\PageIndex{9}\)На малюнку зображений графік\(f\,^{(4)}(x)\) включення\([0,1]\). Зрозуміло, що найбільше значення\(f\,^{(4)}\), в абсолютному значенні, дорівнює 12. Таким чином, ми дозволяємо\(M=12\) і застосовуємо формулу помилки з теореми\(\PageIndex{1}\).
$e_s =\ frac {(1-0) ^5} {180\ точка 4 ^ 4}\ точка 12 = 0,00026.\]
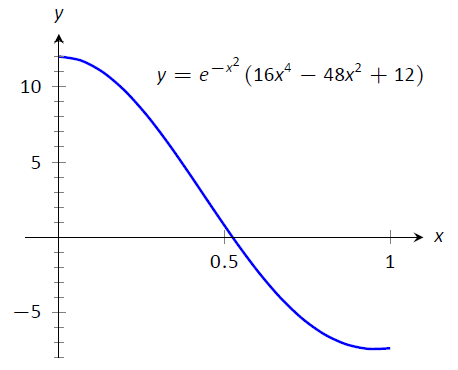
Малюнок\(\PageIndex{10}\): Графік\(f\,^{(4)}(x)\) у прикладі,\(\PageIndex{7}\) щоб допомогти встановити межі помилок.
Наша формула оцінки помилок стверджує, що наше наближення\(0.7468\overline{3}\) знайденого в прикладі\(\PageIndex{5}\) знаходиться в межах 0.00026 від правильної відповіді, отже, ми знаємо, що
$0.74683-0.00026 = .74657\ leq\ int_0^1e^ {-x^2}\ dx\ лек 0.74709 = 0.74683 + 0.00026.\]
Ще раз підтверджуємо обґрунтованість теореми\(\PageIndex{1}\).
На початку цього розділу ми згадали дві основні ситуації, коли числове інтегрування було бажаним. Ми розглянули випадок, коли антипохідне цілого числа неможливо обчислити. Ми зараз досліджуємо ситуацію, коли цілісність невідома. Це, по суті, найбільш широко використовуване застосування методів числового інтегрування. «Більшу частину часу» ми спостерігаємо поведінку, але не знаємо «функції», яка її описує. Замість цього ми збираємо дані про поведінку і робимо наближення на основі цих даних. Ми демонструємо це на прикладі.
Приклад\(\PageIndex{8}\): Approximating distance traveled
Один з авторів відвозив дочку додому зі школи, поки вона записувала їх швидкість кожні 30 секунд. Дані наведені в табл\(\PageIndex{5}\). Приблизна відстань, яку вони пройшли.
Рішення
Нагадаємо, що інтегруючи функцію швидкості, ми отримуємо пройдену відстань. У нас є інформація про\(v(t)\); ми будемо використовувати Правило Сімпсона для наближення\(\int_a^b v(t)\ dt.\)
Найскладнішим аспектом цієї проблеми є перетворення даних у форму, в якій ми повинні бути. Швидкість вимірюється в милі на годину, тоді як час вимірюється з кроком 30 секунд.
| 0 | 0 |
| 1 | 25 |
| 2 | 22 |
| 3 | 19 |
| 4 | 39 |
| 5 | 0 |
| 6 | 43 |
| 7 | 59 |
| 8 | 54 |
| 9 | 51 |
| 10 | 43 |
| 11 | 35 |
| 12 | 40 |
| 13 | 43 |
| 14 | 30 |
| 15 | 0 |
| 16 | 0 |
| 17 | 28 |
| 18 | 40 |
| 19 | 42 |
| 20 | 40 |
| 21 | 39 |
| 22 | 40 |
| 23 | 23 |
| 24 | 0 |
Нам потрібно обчислити\(\ dx = (b-a)/n\). Зрозуміло,\(n=24\). Що таке\(a\) і\(b\)? Оскільки ми починаємо вчасно\(t=0\), ми маємо це\(a=0\). Остаточний записаний час настав через 24 періоди 30 секунд, що становить 12 хвилин або 1/5 години. Таким чином, ми маємо
$\ dx =\ гідророзриву {b-a} {n} =\ гідророзриву {1/5-0} {24} =\ фрак1 {120};\ квад\ гідророзриву {\ dx} {3} =\ гідророзриву {1} {360}.\]
Таким чином пройдена відстань становить приблизно:
\ [\ почати {align*}\ int_0^ {0.2} v (t)\ dt &\ приблизно\ розрив {1} {360}\ Великий [f (x_1) +4f (x_2) + 2f (x_3) +\ cdots + 4f (x_n) +f (x_ {n+1})\ великий]\\
&=\ frac {1} {360}\ Великий [0+4\ cdot25+2\ cdot 2 +\ cdot+ 2\ cdot40+4\ dot 23 + 0\ Великий]\\ &\ приблизно 6.2167\\ текст {милі.} \ end {вирівнювати*}\]
Ми приблизні, автор проїхав 6,2 км. (Оскільки ми впевнені, що читач хоче знати, одометр автора записав відстань приблизно 6,05 миль.)
Ми розпочали цю главу, вивчаючи антипохідні та невизначені інтеграли. Потім ми, здавалося, змінити фокус, дивлячись на області між графіком функції і\(x\) -вісь. Ці області ми визначили як певний інтеграл функції, використовуючи позначення, дуже схоже на позначення невизначеного інтеграла. Фундаментальна теорема обчислення пов'язала ці два, здавалося б, окремих поняття воєдино: ми можемо знайти ділянки під кривою, тобто ми можемо оцінити певний інтеграл, використовуючи антипохідні.
Ми закінчили главу, зазначивши, що антипохідні іноді знайти більш ніж важко: вони неможливі. Тому ми розробили числові методи, які дали нам хороші наближення визначених інтегралів.
Ми використовували певний інтеграл для обчислення площ, а також для обчислення переміщень і пройдених відстаней. Ми можемо зробити набагато більше, ніж це. У розділі 7 ми побачимо більше додатків певного інтеграла. Перед цим у розділі 6 ми вивчимо передові методи інтеграції, аналогічні правилам навчання, таким як правила диференціації продукту, частки та ланцюга.
