4.6: Межі на нескінченності та асимптотах

Last updated
Save as PDF

Page ID: 62206

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Обчисліть межу функції як$x$ збільшення або зменшення без обмежень.
Розпізнайте горизонтальну асимптоту на графіку функції.
Оцініть кінцеву поведінку функції як$x$ збільшення або зменшення без обмежень.
Розпізнайте косу асимптоту на графіку функції.
Проаналізуйте функцію та її похідні, щоб намалювати її графік.

Показано, як використовувати першу та другу похідні функції для опису форми графа. Для побудови графіка функції,$f$ визначеної на необмеженій області, нам також потрібно знати поведінку$f$ as$x→±∞$. У цьому розділі ми визначаємо межі на нескінченності та покажемо, як ці межі впливають на графік функції. В кінці цього розділу ми окреслимо стратегію побудови графіків довільної функції$f$.

Ми почнемо з вивчення того, що означає для функції, щоб мати кінцеву межу на нескінченності. Потім вивчаємо ідею функції з нескінченною межею на нескінченності. Повернувшись у Вступ до функцій та графіків, ми розглянули вертикальні асимптоти; у цьому розділі ми маємо справу з горизонтальними та косими асимптотами.

Межі на нескінченності та горизонтальні асимптоти

Нагадаємо, що$\displaystyle \lim_{x→a}f(x)=L$ засіб$f(x)$ стає довільно близьким до тих$L$ пір, поки$x$ досить близько до$a$. Ми можемо розширити цю ідею до меж нескінченності. Наприклад, розглянемо функцію$f(x)=2+\frac{1}{x}$. Як видно графічно на малюнку$\PageIndex{1}$ і чисельно в таблиці$\PageIndex{1}$, як значення$x$ отримують більше, значення$f(x)$ наближення$2$. Ми говоримо межа як$x$ підходи$∞$$f(x)$ є$2$ і пишемо$\displaystyle \lim_{x→∞}f(x)=2$. Аналогічно$x<0$, для того, як значення$|x|$ стають більшими, значення$f(x)$ наближення$2$. Ми говоримо межа як$x$ підходи$−∞$$f(x)$ є$2$ і пишемо$\displaystyle \lim_{x→−∞}f(x)=2$.

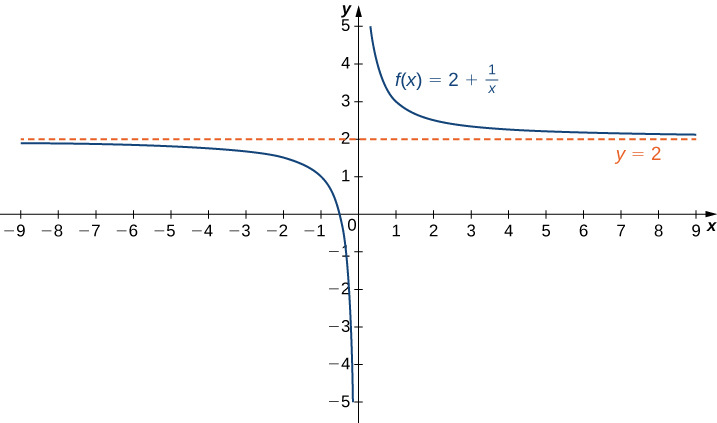
Графічна функція f (x) 2 + 1/x. Функція починається від'ємною поблизу y = 2, але потім зменшується до −∞ поблизу x = 0. Потім функція зменшується від ∞ поблизу x = 0 і наближається до y = 2 при збільшенні x. Існує горизонтальна лінія, що позначає асимптоту y = 2. — Малюнок:$\PageIndex{1}$ Функція наближається до асимптоти як$y=2$ підходи$x$.$±∞$

Таблиця$\PageIndex{1}$: Значення функції$f$ як$x→±∞$
$x$	10	100	1 000	10 000
$2+\frac{1}{x}$	2.1	2.01	2.001	2.0001
$x$	−10	−100	−1000	−10 000
$2+\frac{1}{x}$	1.9	1,99	1.999	1.999

Більш загально, для будь-якої функції$f$, ми говоримо межа як$x→∞$ з$f(x)$ є$L$ якщо$f(x)$ стає довільно близько до тих$L$ пір, поки$x$ досить великий. У такому випадку пишемо$\displaystyle \lim_{x→∞}f(x)=L$. Аналогічно, ми говоримо, що межа$x→−∞$ станом на$f(x)$ є$L$ якщо$f(x)$ стає довільно близькою до тих$L$ пір, поки$x<0$ і$|x|$ є досить великим. У такому випадку пишемо$\displaystyle \lim_{x→−∞}f(x)=L$. Тепер ми розглянемо визначення функції, що має межу на нескінченності.

Визначення: Межа на нескінченність (неформальна)

Якщо значення$f(x)$ стають довільно близькими до$L$ як$x$ стає досить великими, ми говоримо, що функція$f$ має межу на нескінченність і записуємо

\[\lim_{x→∞}f(x)=L. \nonumber \]

Якщо значення$f(x)$ стає довільно близькими до$L$ for$x<0$ as$|x|$ стає досить великими, скажемо, що функція$f$ має межу при негативній нескінченності і запишемо

\[\lim_{x→−∞}f(x)=L. \nonumber \]

Якщо значення$f(x)$ отримують довільно близькі до деякого кінцевого значення$L$ як$x→∞$ or$x→−∞$, графік$f$ наближається до прямої$y=L$. У такому випадку лінія$y=L$ є горизонтальною асимптотою$f$ (рис.$\PageIndex{2}$). Наприклад, для функції$f(x)=\dfrac{1}{x}$, оскільки$\displaystyle \lim_{x→∞}f(x)=0$, лінія$y=0$ є горизонтальною асимптотою$f(x)=\dfrac{1}{x}$.

Фігура розбита на дві фігури, позначені a і b. На малюнку a показано функцію f (x), що наближається, але ніколи не торкається горизонтальної пунктирною лінією, позначеною L зверху. На малюнку b показано функцію f (x), що наближається, але ніколи не горизонтальна пунктирна лінія з позначкою M знизу. — Малюнок$\PageIndex{2}$: (а) Як$x→∞$, значення$f$ стають довільно близькими до$L$. Лінія$y=L$ являє собою горизонтальну асимптоту$f$. (б) Як$x→−∞$, значення$f$ стають довільно близькими до$M$. Лінія$y=M$ являє собою горизонтальну асимптоту$f$.

Визначення: Горизонтальна асимптота

Якщо$\displaystyle \lim_{x→∞}f(x)=L$ або$\displaystyle \lim_{x→−∞}f(x)=L$, ми говоримо, що лінія$y=L$ є горизонтальною асимптотою$f$.

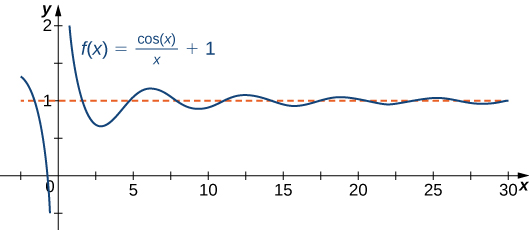
Функція не може перетинати вертикальну асимптоту, оскільки графік повинен наближатися до нескінченності (або$ −∞$) принаймні з одного напрямку, коли$x$ наближається до вертикальної асимптоти. Однак функція може перетинати горизонтальну асимптоту. Насправді функція може перетинати горизонтальну асимптоту необмежену кількість разів. Наприклад, функція,$f(x)=\dfrac{\cos x}{x}+1$ показана на малюнку,$\PageIndex{3}$ перетинає горизонтальну асимптоту$y=1$ нескінченну кількість разів, коли вона коливається навколо асимптоти з постійно спадаючою амплітудою.

Показана функція f (x) = (cos x) /x + 1. Він зменшується від (0, ∞), а потім переходить до коливань навколо y = 1 зі зменшенням амплітуди. — Малюнок$\PageIndex{3}$: Графік$f(x)=(\cos x)/x+1$ перетинає свою горизонтальну асимптоту$y=1$ нескінченну кількість разів.

Алгебраїчні граничні закони та теорема стискання, які ми ввели у Вступ до меж, також застосовуються до меж на нескінченності. Ми ілюструємо, як використовувати ці закони для обчислення декількох меж на нескінченності.

Приклад$\PageIndex{1}$: Computing Limits at Infinity

Для кожної з наведених нижче функцій$f$ оцінюють$\displaystyle \lim_{x→∞}f(x)$ і$\displaystyle \lim_{x→−∞}f(x)$. Визначте горизонтальну асимптоту (и) для$f$.

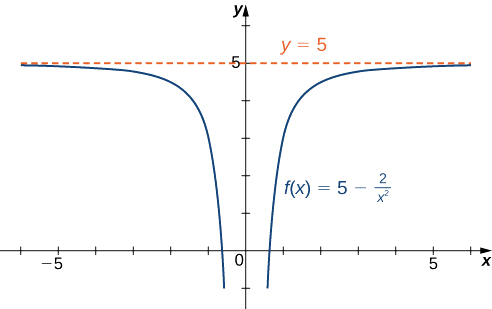
$f(x)=5−\dfrac{2}{x^2}$
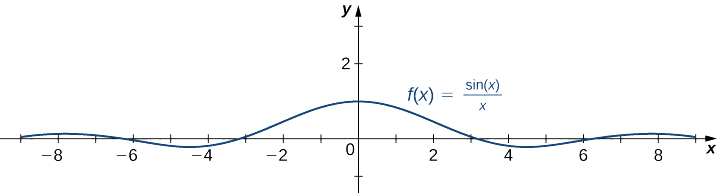
$f(x)=\dfrac{\sin x}{x}$
$f(x)=\tan^{−1}(x)$

Рішення

а Використовуючи алгебраїчні граничні закони, ми маємо

\[\lim_{x→∞}\left(5−\frac{2}{x^2}\right)=\lim_{x→∞}5−2\left(\lim_{x→∞}\frac{1}{x}\right)\cdot\left(\lim_{x→∞}\frac{1}{x}\right)=5−2⋅0=5.\nonumber \]

Аналогічно,$\displaystyle \lim_{x→−∞}f(x)=5$. Тому$f(x)=5-\dfrac{2}{x^2}$ має горизонтальну асимптоту$y=5$ і$f$ наближається до цієї горизонтальної асимптоти$x→±∞$, як показано на наступному графіку.

Графічна функція f (x) = 5 — 2/x2. Функція наближається до горизонтальної асимптоти y = 5, оскільки x наближається до ±∞. — Малюнок$\PageIndex{4}$: Ця функція наближається до горизонтальної асимптоти як$x→±∞.$

б. оскільки$-1≤\sin x≤1$ для всіх$x$ у нас є

\[\frac{−1}{x}≤\frac{\sin x}{x}≤\frac{1}{x}\nonumber \]

для всіх$x≠0$. Крім того, так як

$\displaystyle \lim_{x→∞}\frac{−1}{x}=0=\lim_{x→∞}\frac{1}{x}$,

ми можемо застосувати теорему стискання, щоб зробити висновок, що

$\displaystyle \lim_{x→∞}\frac{\sin x}{x}=0.$

Аналогічно,

$\displaystyle \lim_{x→−∞}\frac{\sin x}{x}=0.$

Таким чином,$f(x)=\dfrac{\sin x}{x}$ має горизонтальну асимптоту$y=0$ і$f(x)$ наближається до цієї горизонтальної асимптоти$x→±∞$, як показано на наступному графіку.

Показана функція f (x) = (sin x) /x. Він має глобальний максимум при (0, 1), а потім продовжує коливатися навколо y = 0 зі зменшенням амплітуди. — Малюнок$\PageIndex{5}$: Ця функція багаторазово перетинає свою горизонтальну асимптоту.

c Для оцінки$\displaystyle \lim_{x→∞}\tan^{−1}(x)$ і$\displaystyle \lim_{x→−∞}\tan^{−1}(x)$, спочатку розглянемо графік$y=\tan(x)$ над інтервалом,$\left(−\frac{π}{2},\frac{π}{2}\right)$ як показано на наступному графіку.

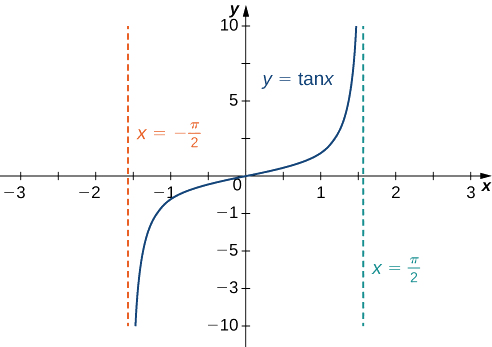
Показана функція f (x) = tan x. Вона збільшується від (−π/2, −∞), проходить через початок, а потім збільшується в бік (π/2, ∞). Існують вертикальні пунктирні лінії, що позначають x = ± π/2. — Малюнок$\PageIndex{6}$: Графік$y=\tan x$ має вертикальні асимптоти при$x=±\frac{π}{2}$

Так як

$\displaystyle \lim_{x→\tfrac{π}{2}^−}\tan x=∞,$

з цього випливає, що

$\displaystyle \lim_{x→∞}\tan^{−1}(x)=\frac{π}{2}.$

Аналогічно, так як

$\displaystyle \lim_{x→-\tfrac{π}{2}^+}\tan x=−∞,$

з цього випливає, що

$\displaystyle \lim_{x→−∞}\tan^{−1}(x)=−\frac{π}{2}.$

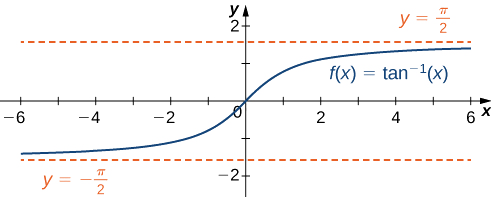
В результаті$y=\frac{π}{2}$ і$y=−\frac{π}{2}$ є горизонтальними асимптотами,$f(x)=\tan^{−1}(x)$ як показано на наступному графіку.

Буде показано функцію f (x) = tan−1 x. Вона збільшується від (−∞, −π/2), проходить через початок, а потім збільшується в бік (∞, π/2). Існують горизонтальні пунктирні лінії, що позначають y = ± π/2. — Рисунок$\PageIndex{7}$: Ця функція має два горизонтальних асимптоти.

Вправа$\PageIndex{1}$

Оцініть$\displaystyle \lim_{x→−∞}\left(3+\frac{4}{x}\right)$ і$\displaystyle \lim_{x→∞}\left(3+\dfrac{4}{x}\right)$. Визначте горизонтальні асимптоти,$f(x)=3+\frac{4}{x},$ якщо такі є.

Підказка: $\displaystyle \lim_{x→±∞}\frac{1}{x}=0$

Відповідь: Обидві межі$3.$ є Лінія$y=3$ є горизонтальною асимптотою.

Нескінченні межі і нескінченність

Іноді значення функції$f$ стають довільно великими як$x→∞ $ (або як$x→−∞$). В даному випадку пишемо$\displaystyle \lim_{x→∞}f(x)=∞$ (або$\displaystyle \lim_{x→−∞}f(x)=∞$). З іншого боку, якщо значення$f$ від'ємні, але стають довільно великими за величиною як$x→∞$ (або як$x→−∞$), ми пишемо$\displaystyle \lim_{x→∞}f(x)=−∞$ (або$\displaystyle \lim_{x→−∞}f(x)=−∞$).

Наприклад, розглянемо функцію$f(x)=x^3$. Як видно з таблиці$\PageIndex{2}$ та малюнка$\PageIndex{8}$, так як$x→∞$ значення$f(x)$ стають довільно великими. Тому,$\displaystyle \lim_{x→∞}x^3=∞$. З іншого боку, як$x→−∞$, значення$f(x)=x^3$ негативні, але стають довільно великими за величиною. Отже,$\displaystyle \lim_{x→−∞}x^3=−∞.$

Таблиця$\PageIndex{2}$: Значення силової функції як$x→±∞$
$x$	10	20	50	100	1000
$x^3$	1000	8000	125 000	1 000 000	1 000 000 000
$x$	−10	−20	−50	−100	−1000
$x^3$	−1000	−8000	−125 000	−1 000 000	−1 000 000 000

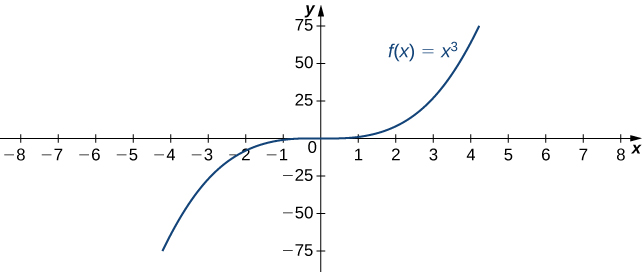
Графічна функція f (x) = x3. Очевидно, що ця функція стрімко наближається до нескінченності, коли х наближається до — Малюнок$\PageIndex{8}$: Для цієї функції функціональні значення наближаються до$±$ нескінченності як$x→±∞.$

Визначення: Нескінченна межа і нескінченність (неформа

Ми говоримо, що функція$f$ має нескінченну межу в нескінченності і записувати

\[\lim_{x→∞}f(x)=∞. \nonumber \]

якщо$f(x)$ стає довільно великим для$x$ досить великих. Ми говоримо, що функція має негативну нескінченну межу на нескінченності і записуємо

\[\lim_{x→∞}f(x)=−∞. \nonumber \]

якщо$f(x)<0$ і$|f(x)|$ стає довільно великим для$x$ досить великих. Аналогічно, ми можемо визначити нескінченні межі як$x→−∞.$

Формальні визначення

Раніше ми використовували терміни довільно закритий, довільно великий і досить великий, щоб визначити межі на нескінченності неформально. Хоча ці терміни дають точні описи меж на нескінченності, вони не є точними математично. Ось більш формальні визначення меж на нескінченності. Потім ми розглянемо, як використовувати ці визначення, щоб довести результати, пов'язані з межами на нескінченності.

Визначення: Межа на нескінченність (формальна)

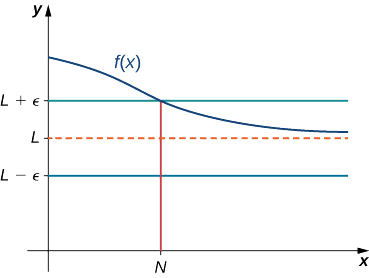
Ми говоримо, що функція$f$ має межу на нескінченності, якщо існує дійсне число$L$ таке$ε>0$, що для всіх існує$N>0$ таке, що

\[|f(x)−L|<ε \nonumber \]

для всіх$x>N.$ в такому випадку ми пишемо

\[\lim_{x→∞}f(x)=L \nonumber \]

Функція f (x) графічна, і вона має горизонтальну асимптоту на L. L позначена на осі y, як і L + і L —. На осі х N позначається як значення х таке, що f (x) = L +. — Малюнок$\PageIndex{9}$: Для функції з обмеженням на нескінченність, для всіх$x>N, |f(x)−L|<ε.$

Раніше в цьому розділі ми використовували графічні докази на малюнку$\PageIndex{1}$ та числові докази в таблиці,$\PageIndex{1}$ щоб зробити висновок про це$\displaystyle \lim_{x→∞}\left(2+\frac{1}{x}\right)=2$. Тут ми використовуємо формальне визначення межі на нескінченності, щоб суворо довести цей результат.

Приклад$\PageIndex{2}$:

Скористайтеся формальним визначенням межі на нескінченності, щоб довести це$\displaystyle \lim_{x→∞}\left(2+\frac{1}{x}\right)=2$.

Рішення

$ε>0.$Нехай$N=\frac{1}{ε}$. Тому для всіх$x>N$ у нас є

\[\left|2+\frac{1}{x}−2\right|=\left|\frac{1}{x}\right|=\frac{1}{x}<\frac{1}{N}=ε \nonumber \]

Вправа$\PageIndex{2}$

Скористайтеся формальним визначенням межі на нескінченності, щоб довести це$\displaystyle \lim_{x→∞}\left(3-\frac{1}{x^2}\right)=3$.

Підказка: Нехай$N=\frac{1}{\sqrt{ε}}$.

Відповідь

$ε>0.$Нехай$N=\frac{1}{\sqrt{ε}}$. Тому для всіх у$x>N,$ нас є

\[\Big|3−\frac{1}{x^2}−3\Big|=\frac{1}{x^2}<\frac{1}{N^2}=ε \nonumber \]

Тому,$\displaystyle \lim_{x→∞}(3−1/x^2)=3.$

Тепер звернемо увагу на більш точне визначення нескінченної межі на нескінченності.

Визначення: Нескінченна межа і нескінченність (формальна

Ми говоримо, що функція$f$ має нескінченну межу в нескінченності і записувати

$\displaystyle \lim_{x→∞}f(x)=∞$

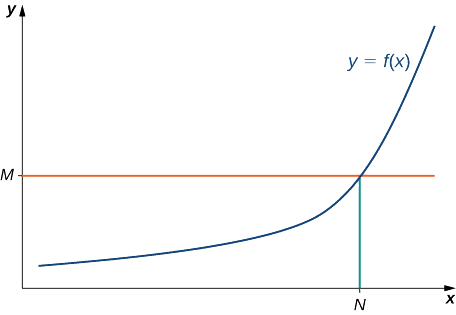
якщо для всіх$M>0,$ існує$N>0$ таке, що

$f(x)>M$

для всіх$x>N$ (див. Рис.$\PageIndex{10}$).

Ми говоримо, що функція має негативну нескінченну межу на нескінченності і записуємо

$\displaystyle \lim_{x→∞}f(x)=−∞$

якщо для всіх$M<0$, існує$N>0$ таке, що

$f(x)<M$

для всіх$x>N$.

Аналогічно ми можемо визначити межі як$x→−∞.$

Функція f (x) графічна. Вона продовжує швидко збільшуватися після х = N, а f (N) = M. — Малюнок$\PageIndex{10}$: Для функції з нескінченною межею на нескінченності, для всіх$x>N,\; f(x)>M.$

Раніше ми використовували графічні докази (рис.$\PageIndex{8}$) та числові докази (таблиця$\PageIndex{2}$), щоб зробити висновок про це$\displaystyle \lim_{x→∞}x^3=∞$. Тут ми використовуємо формальне визначення нескінченної межі на нескінченності, щоб довести цей результат.

Приклад$\PageIndex{3}$

Використовуйте формальне визначення нескінченної межі на нескінченності, щоб довести, що$\displaystyle \lim_{x→∞}x^3=∞.$

Рішення

$M>0.$Нехай$N=\sqrt[3]{M}$. Тоді, для всіх$x>N$, у нас є

$x^3>N^3=(\sqrt[3]{M})^3=M.$

Тому,$\displaystyle \lim_{x→∞}x^3=∞$.

Вправа$\PageIndex{3}$

Використовуйте формальне визначення нескінченної межі на нескінченності, щоб довести, що$\displaystyle \lim_{x→∞}3x^2=∞.$

Підказка: Нехай$N=\sqrt{\frac{M}{3}}$.

Відповідь

$M>0.$Нехай$N=\sqrt{\frac{M}{3}}$. Тоді для всіх у$x>N,$ нас є

$3x^2>3N^2=3\left(\sqrt{\frac{M}{3}}\right)^2=\frac{3M}{3}=M$

Поведінка кінця

Поведінка функції, як$x→±∞$ називається кінцевою поведінкою функції. На кожному з кінців функції функція може проявляти один з наступних типів поведінки:

Функція$f(x)$ наближається до горизонтальної асимптоти$y=L$.
Функція$f(x)→∞$ або$f(x)→−∞.$
Функція не наближається до кінцевої межі, а також не наближається$∞$ або$−∞$. При цьому функція може мати деяку коливальну поведінку.

Розглянемо кілька класів функцій тут і розглянемо різні типи кінцевої поведінки для цих функцій.

Поведінка кінця для поліноміальних функцій

Розглянемо функцію power$f(x)=x^n$, де$n$ є додатним цілим числом. З малюнка$\PageIndex{11}$ та$\PageIndex{12}$ малюнка ми бачимо, що

\[\lim_{x→∞}x^n=∞;\;n=1,2,3,… \nonumber \]

\[\lim_{x→−∞}x^n=\begin{cases}∞, & n=2,4,6,…\\−∞, & n=1,3,5,….\end{cases} \nonumber \]

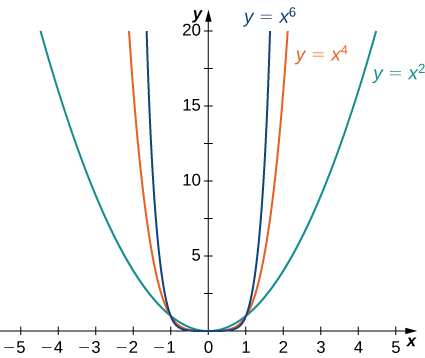
Функції x2, x4 та x6 графічні, і очевидно, що з ростом показника функції збільшуються швидше. — Малюнок$\PageIndex{11}$: Для силових функцій з рівномірною потужністю$n$,$\displaystyle \lim_{x→∞}x^n=∞=\lim_{x→−∞}x^n$.

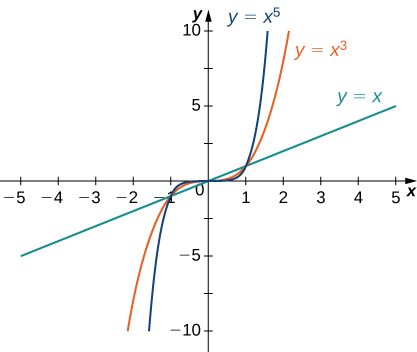
Функції x, x3 та x5 графічні, і очевидно, що з ростом показника функції збільшуються швидше. — Малюнок$\PageIndex{12}$: Для силових функцій з непарною потужністю$n$,$\displaystyle \lim_{x→∞}x^n=∞$ і$\displaystyle \lim_{x→−∞}x^n=−∞.$

Використовуючи ці факти, не важко оцінити$\displaystyle \lim_{x→∞}cx^n$ і$\displaystyle \lim_{x→−∞}cx^n$, де$c$ будь-яка константа і$n$ є натуральним числом. Якщо$c>0$, графік$y=cx^n$ є вертикальним розтягуванням або стисненням$y=x^n,$ і тому

$\displaystyle \lim_{x→∞}cx^n=\lim_{x→∞}x^n$і$\displaystyle \lim_{x→−∞}cx^n=\lim_{x→−∞}x^n$ якщо$c>0$.

Якщо графік$c<0,$$y=cx^n$ є вертикальним розтягуванням або стисненням в поєднанні з відображенням про$x$ -осі, а отже

$\displaystyle \lim_{x→∞}cx^n=−\lim_{x→∞}x^n$і$\displaystyle \lim_{x→−∞}cx^n=−\lim_{x→−∞}x^n$ якщо$c<0.$

Якщо$c=0,y=cx^n=0,$ в якому випадку$\displaystyle \lim_{x→∞}cx^n=0=\lim_{x→−∞}cx^n.$

Приклад$\PageIndex{4}$: Limits at Infinity for Power Functions

Для кожної функції$f$ оцінюють$\displaystyle \lim_{x→∞}f(x)$ і$\displaystyle \lim_{x→−∞}f(x)$.

$f(x)=−5x^3$
$f(x)=2x^4$

Рішення

Оскільки коефіцієнт$x^3$ є$−5$, графік$f(x)=−5x^3$ передбачає вертикальне розтягування і відображення графіка$y=x^3$ про$x$ -осі. Тому$\displaystyle \lim_{x→∞}(−5x^3)=−∞$ і$\displaystyle \lim_{x→−∞}(−5x^3)=∞$.
Оскільки коефіцієнт$x^4$ є$2$, то графік$f(x)=2x^4$ є вертикальним розтягненням графіка$y=x^4$. Тому$\displaystyle \lim_{x→∞}2x^4=∞$ і$\displaystyle \lim_{x→−∞}2x^4=∞$.

Вправа$\PageIndex{4}$

Нехай$f(x)=−3x^4$. Знайти$\displaystyle \lim_{x→∞}f(x)$.

Підказка: $−3$Коефіцієнт негативний.

Відповідь: $−∞$

Тепер ми розглянемо, як межі нескінченності для степеневих функцій можуть бути використані$\displaystyle \lim_{x→±∞}f(x)$ для визначення для будь-якої поліноміальної функції$f$. Розглянемо поліноміальну функцію

\[f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a^1x+a^0 \nonumber \]

ступеня$n≥1$ так, що$a_n≠0.$

Факторинг, ми бачимо, що

\[f(x)=a_nx^n\left(1+\frac{a_{n−1}}{a_n}\frac{1}{x}+…+\frac{a_1}{a_n}\frac{1}{x^{n−1}}+\frac{a_0}{a_n}\frac{1}{x^n}\right). \nonumber \]

Оскільки$x→±∞,$ всі терміни всередині дужок наближаються до нуля, крім першого члена. Ми робимо висновок, що

\[\lim_{x→±∞}f(x)=\lim_{x→±∞}a_nx^n. \nonumber \]

Наприклад, функція$f(x)=5x^3−3x^2+4$ поводиться так,$g(x)=5x^3$$x→±∞$ як показано на малюнку$\PageIndex{13}$ та таблиці$\PageIndex{3}$.

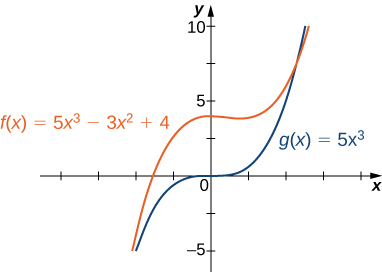
Обидві функції f (x) = 5x3 — 3x2 + 4 і g (x) = 5x3 побудовані. Їх поведінка для великих позитивних і великих негативних чисел сходиться. — Малюнок$\PageIndex{13}$: Кінцева поведінка многочлена визначається поведінкою терміна з найбільшим показником.

Таблиця$\PageIndex{3}$: Кінцева поведінка полінома визначається терміном з найбільшим показником
$x$	10	100	1000
$f(x)=5x^3−3x^2+4$	4704	4 970 004	4 997 000 004
$g(x)=5x^3$	5000	5 000 000	5 000 000 000
$x$	−10	−100	−000
$f(x)=5x^3−3x^2+4$	−5296	−5 029 996	−5 002 999 996
$g(x)=5x^3$	−5000	−5 000 000	−5 000 000 000

Поведінка кінця для алгебраїчних функцій

Кінцева поведінка для раціональних функцій і функцій за участю радикалів трохи складніше, ніж для поліномів. У прикладі показано$\PageIndex{5}$, що межі на нескінченності раціональної функції$f(x)=\dfrac{p(x)}{q(x)}$ залежать від співвідношення між ступенем чисельника і ступенем знаменника. Для оцінки меж на нескінченності для раціональної функції ділимо чисельник і знаменник на найвищу$x$ ступінь присутності в знаменнику. Це визначає, який термін у загальному виразі домінує над поведінкою функції при великих значеннях$x$.

Приклад$\PageIndex{5}$: Determining End Behavior for Rational Functions

Для кожної з наведених нижче функцій визначте межі,$x→∞$ а$x→−∞.$ потім використовуйте цю інформацію для опису кінцевої поведінки функції.

$f(x)=\dfrac{3x−1}{2x+5}$(Примітка: Ступінь чисельника і знаменника однакові.)
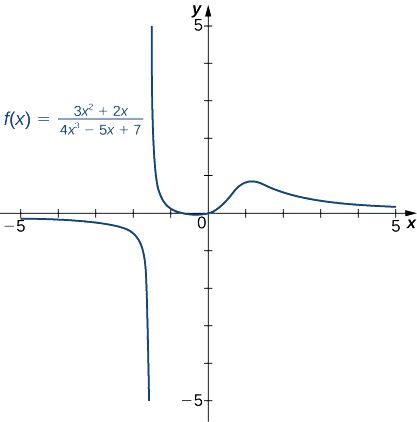
$f(x)=\dfrac{3x^2+2x}{4x^3−5x+7}$(Примітка: Ступінь чисельника менше ступеня знаменника.)
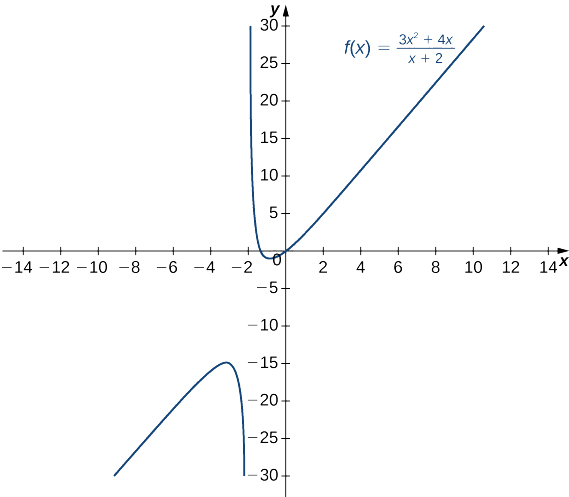
$f(x)=\dfrac{3x^2+4x}{x+2}$(Примітка: Ступінь чисельника більше, ніж ступінь знаменника.)

Рішення

а. найвища сила$x$ в знаменнику є$x$. Тому, розділивши чисельник і знаменник на$x$ і застосовуючи алгебраїчні граничні закони, ми бачимо, що

\[ \begin{align*} \lim_{x→±∞}\frac{3x−1}{2x+5} &=\lim_{x→±∞}\frac{3−1/x}{2+5/x} \\[4pt] &=\frac{\lim_{x→±∞}(3−1/x)}{\lim_{x→±∞}(2+5/x)} \\[4pt] &=\frac{\lim_{x→±∞}3−\lim_{x→±∞}1/x}{\lim_{x→±∞}2+\lim_{x→±∞}5/x} \\[4pt] &=\frac{3−0}{2+0}=\frac{3}{2}. \end{align*}\]

Оскільки$\displaystyle \lim_{x→±∞}f(x)=\frac{3}{2}$, ми знаємо, що$y=\frac{3}{2}$ це горизонтальна асимптота для цієї функції, як показано на наступному графіку.

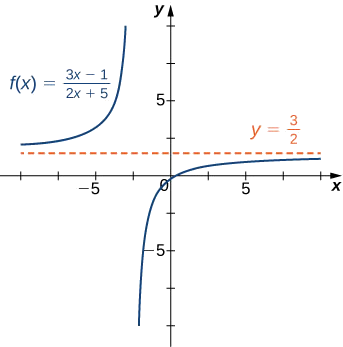
Пара криволінійних графіків. Перший починається з лівого боку фігури, де вона майже рівна зі значенням Y 3 над 2, потім згинається майже до вертикалі, залишаючи верхню частину фігури на X дорівнює негативним 5 половинам. Інша крива піднімається майже вертикально знизу, коли X дорівнює негативним 5 половинам, вирівнюється, і стає майже горизонтальною праворуч зі значенням Y близько 3 половин — Рисунок$\PageIndex{14}$: Графік цієї раціональної функції наближається до горизонтальної асимптоти як$x→±∞.$

б. оскільки найбільша сила$x$ появи в знаменнику дорівнює$x^3$, ділимо чисельник і знаменник на$x^3$. Зробивши це і застосувавши алгебраїчні граничні закони, отримуємо

\[\lim_{x→±∞}\frac{3x^2+2x}{4x^3−5x+7}=\lim_{x→±∞}\frac{3/x+2/x^2}{4−5/x^2+7/x^3}=\frac{3\cdot 0+2\cdot 0}{4−5\cdot 0+7\cdot 0}=\frac{0}{4}=0. \nonumber \]

Тому$f$ має горизонтальну асимптоту$y=0$, як показано на наступному графіку.

Функція f (x) = (3x2 + 2x)/(4x2 — 5x + 7) побудована як її горизонтальна асимптота при y = 0. — Рисунок$\PageIndex{15}$: Графік цієї раціональної функції наближається до горизонтальної асимптоти$y=0$ як$x→±∞.$

с. розділивши чисельник і знаменник на$x$, маємо

\[\displaystyle \lim_{x→±∞}\frac{3x^2+4x}{x+2}=\lim_{x→±∞}\frac{3x+4}{1+2/x}. \nonumber \]

Як$x→±∞$, наближається знаменник$1$. Як$x→∞$, наближається чисельник$+∞$. Як$x→−∞$, наближається чисельник$−∞$. $\displaystyle \lim_{x→∞}f(x)=∞$Тому тоді$\displaystyle \lim_{x→−∞}f(x)=−∞$ як показано на наступному малюнку.

Наноситься функція f (x) = (3x2 + 4x)/(х + 2). Здається, він має діагональну асимптоту, а також вертикальну асимптоту при x = −2. — Малюнок$\PageIndex{16}$: Як$x→∞$, значення$f(x)→∞$. Як$x→−∞$, значення$f(x)→−∞.$

Вправа$\PageIndex{5}$

Оцініть$\displaystyle \lim_{x→±∞}\frac{3x^2+2x−1}{5x^2−4x+7}$ і використовуйте ці межі для визначення кінцевої поведінки$f(x)=\dfrac{3x^2+2x−1}{5x^2−4x+7}$.

Підказка: Розділіть чисельник і знаменник на$x^2$.

Відповідь: $\frac{3}{5}$

Перш ніж приступити, розглянемо графік,$f(x)=\dfrac{3x^2+4x}{x+2}$ показаний на малюнку$\PageIndex{16}$. Як$x→∞$ і$x→−∞$, графік$f$ представляється майже лінійним. Хоча$f$ це, звичайно, не лінійна функція, ми зараз досліджуємо, чому графік,$f$ здається, наближається до лінійної функції. По-перше, використовуючи довге ділення многочленів, ми можемо записати

\[f(x)=\frac{3x^2+4x}{x+2}=3x−2+\frac{4}{x+2}. \nonumber \]

Оскільки$\dfrac{4}{x+2}→0$, як$x→±∞,$ ми робимо висновок, що

\[ \lim_{x→±∞}(f(x)−(3x−2))=\lim_{x→±∞}\frac{4}{x+2}=0. \nonumber \]

Тому графік$f$ наближається до лінії$y=3x−2$ як$x→±∞$. Ця лінія відома як коса асимптота для$f$ (рис.$\PageIndex{17}$).

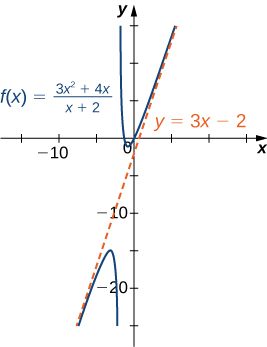
Функція f (x) = (3x2 + 4x)/(x + 2) побудована як її діагональна асимптота y = 3x — 2. — Рисунок$\PageIndex{17}$: Графік раціональної функції$f(x)=(3x^2+4x)/(x+2)$ наближається до косої асимптоти$y=3x−2$ як$x→±∞.$

Ми можемо узагальнити результати Прикладу,$\PageIndex{5}$ щоб зробити наступний висновок щодо кінцевої поведінки для раціональних функцій. Розглянемо раціональну функцію

\[f(x)=\frac{p(x)}{q(x)}=\frac{a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0}{b_mx^m+b_{m−1}x^{m−1}+…+b_1x+b_0},\nonumber \]

де$a_n≠0$ і$b_m≠0.$

Якщо ступінь чисельника збігається зі ступенем знаменника,$(n=m),$ то$f$ має горизонтальну асимптоту$y=a_n/b_m$ як$x→±∞.$
Якщо ступінь чисельника менше ступеня знаменника,$(n<m),$ то$f$ має горизонтальну асимптоту$y=0$ як$x→±∞.$
Якщо ступінь чисельника більше ступеня знаменника,$(n>m),$ то$f$ не має горизонтальної асимптоти. Межі на нескінченності - це або позитивна, або негативна нескінченність, в залежності від знаків провідних членів. Крім того, використовуючи довгий ділення, функція може бути переписана як\[f(x)=\frac{p(x)}{q(x)}=g(x)+\frac{r(x)}{q(x)}, \nonumber \] там, де ступінь менше ступеня$q(x)$.$r(x)$ Як результат,$\displaystyle \lim_{x→±∞}r(x)/q(x)=0$. Тому значення$[f(x)−g(x)]$ наближаються до нуля як$x→±∞$. Якщо ступінь$p(x)$ рівно на один більше ступеня$q(x)$ (тобто$n=m+1$), функція$g(x)$ є лінійною функцією. В даному випадку ми називаємо косу$g(x)$ асимптоту.

Тепер розглянемо кінцеву поведінку для функцій, що беруть участь радикал.

Приклад$\PageIndex{6}$: Determining End Behavior for a Function Involving a Radical

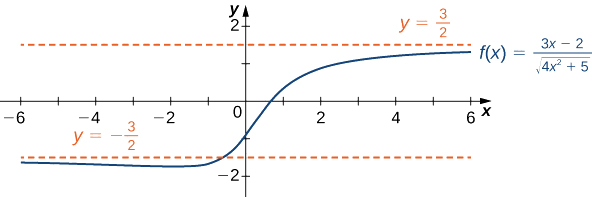
Знайдіть межі як$x→∞$ і$x→−∞$ для$f(x)=\dfrac{3x−2}{\sqrt{4x^2+5}}$ і опишіть кінцеву поведінку$f$.

Рішення

Скористаємося тією ж стратегією, що і для раціональних функцій: ділимо чисельник і знаменник на ступінь$x$. Щоб визначити відповідну силу$x$, розглянемо вираз$\sqrt{4x^2+5}$ в знаменнику. Так як

\[\sqrt{4x^2+5}≈\sqrt{4x^2}=2|x| \nonumber \]

для великих значень чинності$x$$x$ з'являється якраз до першого ступеня в знаменнику. Тому числівник і знаменник ділимо на$|x|$. Потім, використовуючи те, що$|x|=x$$x>0, |x|=−x$ для$x<0$, і$|x|=\sqrt{x^2}$ для всіх$x$, розраховуємо межі наступним чином:

\ [\ почати {вирівнювати*}\ lim_ {x→∞}\ розрив {3x−2} {\ sqrt {4x^2+5}} &=\ lim_ {x→∞}\ frac {(1/|x|)} {(1/|x|)\ sqrt {4x^2+5}}\\ [4pt]
&=\ lim_ {x→∞}\ розрив {(1/x) (3х−2)} {\ sqrt {(1/x^2) (4x^2+5)}}\\ [4pt]
&=\ lim_ {x→∞}\ frac {3−2/x} {\ sqrt {4+5/x^2}} =\ frac {3} {\ sqrt {4}} =\ frac 3} {2}\ end {вирівнювати*}\]

\ [\ почати {вирівнювати*}\ lim_ {x→−∞}\ розрив {3x−2} {\ sqrt {4x^2+5}} &=\ lim_ {x→∞}\ frac {(1/|x|)} {(1/|x|)\ sqrt {4x^2+5}}\\ [4pt]
&=\ lim_ x→−∞}\ розрив {(−1/x) (3х−2)} {\ sqrt {(1/x^2) (4x^2+5)}}\\ [4pt]
&=\ lim_ {x→−∞}\ frac {−3+2/x} {\ sqrt {4+5/x^2}} =\ frac {−3} {\ sqrt {4}} =\ гідророзриву {−3} {2}. \ end {вирівнювати*}\]

Тому$f(x)$ наближається до горизонтальної асимптоти$y=\frac{3}{2}$ як$x→∞$ і до горизонтальної асимптоти$x→−∞$,$y=−\frac{3}{2}$ як показано на наступному графіку.

Побудовано функцію f (x) = (3x − 2)/(квадратний корінь величини (4x2 + 5)). Він має два горизонтальних асимптоти при y = ± 3/2, і він перетинає y = −3/2 перед тим, як сходитися до нього знизу. — Рисунок$\PageIndex{18}$: Ця функція має два горизонтальних асимптоти і перетинає один з асимптотів.

Вправа$\PageIndex{6}$

Оцініть$\displaystyle \lim_{x→∞}\frac{\sqrt{3x^2+4}}{x+6}$.

Підказка: Розділіть чисельник і знаменник на$x$.

Відповідь: $\sqrt{3}$

Визначення кінцевої поведінки трансцендентних функцій

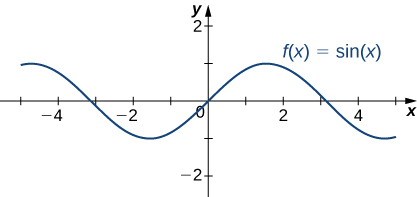
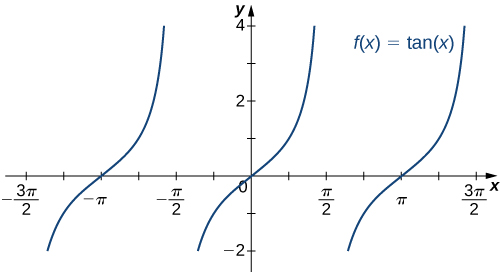
Шість основних тригонометричних функцій є періодичними і не наближаються до кінцевої межі, як$x→±∞.$ Наприклад,$\sin x$ коливається між 1 і −1 (рис.$\PageIndex{19}$). Тангенсна функція$x$ має нескінченну кількість вертикальних асимптотів як$x→±∞$; отже, вона не наближається до кінцевої межі і не наближається,$±∞$$x→±∞$ як показано на малюнку$\PageIndex{20}$.

Графічна функція f (x) = sin x. — Малюнок$\PageIndex{19}$: Функція$f(x)=\sin x$ коливається між$1$ і$−1$ як$x→±∞$

Графічна функція f (x) = tan x. — Малюнок$\PageIndex{20}$: Функція$f(x)=\tan x$ не наближається до межі і не наближається$±∞$ як$x→±∞$

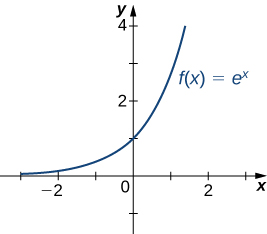
Нагадаємо, що для будь-якої бази функція$b>0,\; b≠1,$$y=b^x$ є експоненціальною функцією з доменом$(−∞,∞)$ і діапазоном$(0,∞)$. Якщо$b>1,\;y=b^x$ збільшується більше$(−∞,∞)$. Якщо$0<b<1, \; y=b^x$ зменшується над$(−∞,∞).$ Для природної експоненціальної функції$f(x)=e^x, \; e≈2.718>1$. Тому$f(x)=e^x$ збільшується$(−∞,∞)$ і діапазон є$(0,∞)$. Експоненціальна функція$f(x)=e^x$ підходить$∞$ як$x→∞$ і наближається$x→−∞$,$0$ як показано в таблиці$\PageIndex{4}$ та рисунку$\PageIndex{21}$.

Таблиця$\PageIndex{4}$: Кінцева поведінка природної експоненціальної функції
$x$	−5	−2	0	2	5
$e^x$	0,00674	0,135	1	7.389	148.413

Функція f (x) = ex позначена графіком. — Рисунок$\PageIndex{21}$: Експоненціальна функція наближається до нуля як$x→−∞$ і наближається$∞$ як$x→∞.$

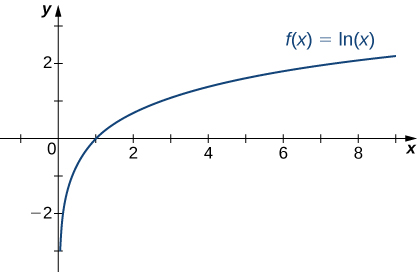
Нагадаємо, що натуральна функція логарифма$f(x)=\ln(x)$ є оберненою природною експоненціальною функцією$y=e^x$. Тому домен$f(x)=\ln(x)$ is$(0,∞)$ і діапазон є$(−∞,∞)$. Графік$f(x)=\ln(x)$ - це відображення графіка$y=e^x$ про пряму$y=x$. Тому$\ln(x)→−∞$ як$x→0^+$ і так,$\ln(x)→∞$$x→∞$ як показано на малюнку$\PageIndex{22}$ і табл$\PageIndex{5}$.

Таблиця$\PageIndex{5}$: Кінцева поведінка функції натурального логарифма
$x$	0,01	0.1	1	10	100
$\ln(x)$	−4.605	−2.303	0	2.303	4.605

Графічна функція f (x) = ln (x). — Малюнок$\PageIndex{22}$: Функція натурального логарифма наближається$∞$ як$x→∞.$

Приклад$\PageIndex{7}$: Determining End Behavior for a Transcendental Function

Знайдіть межі як$x→∞$ і$x→−∞$ для$f(x)=\dfrac{2+3e^x}{7−5e^x}$ та опишіть кінцеву поведінку$f.$

Рішення

Щоб знайти межу як$x→∞,$ розділити чисельник і знаменник на$e^x$:

\[ \begin{align*} \lim_{x→∞}f(x) &= \lim_{x→∞}\frac{2+3e^x}{7−5e^x} \\[4pt] &=\lim_{x→∞}\frac{(2/e^x)+3}{(7/e^x)−5.} \end{align*}\]

Як показано на малюнку$\PageIndex{21}$,$e^x→∞$ як$x→∞$. Тому,

$\displaystyle \lim_{x→∞}\frac{2}{e^x}=0=\lim_{x→∞}\frac{7}{e^x}$.

Зроблено висновок про те$\displaystyle \lim_{x→∞}f(x)=−\frac{3}{5}$, що і графік$f$ наближень до горизонтальної$x→∞.$ асимптоти$y=−\frac{3}{5}$ як, щоб знайти межу як$x→−∞$, використовують той факт, що$e^x→0$ як$x→−∞$ зробити висновок$\displaystyle \lim_{x→-∞}f(x)=\frac{2}{7}$, що, а отже, графік$f(x)$ наближається до горизонтальної асимптоти $y=\frac{2}{7}$як$x→−∞$.

Вправа$\PageIndex{7}$

Знайдіть межі як$x→∞$ і$x→−∞$ для$f(x)=\dfrac{3e^x−4}{5e^x+2}$.

Підказка: $\displaystyle \lim_{x→∞}e^x=∞$і$\displaystyle \lim_{x→-∞}e^x=0.$

Відповідь: $\displaystyle \lim_{x→∞}f(x)=\frac{3}{5}, \quad\lim_{x→−∞}f(x)=−2$

Рекомендації щодо малювання графіка функції

Тепер у нас є достатньо аналітичних інструментів для малювання графіків найрізноманітніших алгебраїчних і трансцендентних функцій. Перш ніж показати, як графікувати конкретні функції, давайте розглянемо загальну стратегію, яку слід використовувати при графіку будь-якої функції.

Стратегія вирішення проблем: креслення графіка функції

З огляду на функцію$f$, скористайтеся наступними кроками, щоб намалювати графік$f$:

Визначте область функції.
Знайдіть$x$ - і$y$ -перехоплює.
$\displaystyle \lim_{x→−∞}f(x)$Оцінити$\displaystyle \lim_{x→∞}f(x)$ і визначити кінцеву поведінку. Якщо будь-яка з цих меж є кінцевим числом$L$, то$y=L$ це горизонтальна асимптота. Якщо будь-яка з цих меж є$∞$ або$−∞$, визначте, чи$f$ має косу асимптоту. Якщо$f$ раціональна функція така$f(x)=\dfrac{p(x)}{q(x)}$, що, де ступінь чисельника більше ступеня знаменника, то$f$ може бути записана як\[f(x)=\frac{p(x)}{q(x)}=g(x)+\frac{r(x)}{q(x),} \nonumber \] де ступінь менше ступеня$q(x)$.$r(x)$ Значення$f(x)$ наближаються до значень$g(x)$ як$x→±∞$. Якщо$g(x)$ є лінійною функцією, вона відома як коса асимптота.
Визначте$f$, чи має вертикальні асимптоти.
Обчисліть$f′.$ Знайти всі критичні точки і визначити інтервали$f$, де збільшується, а де$f$ зменшується. Визначте, чи$f$ має якась локальна крайність.
Обчисліть.$f''.$ Визначте проміжки, де$f$ увігнутий вгору,$f$ а де увігнутий вниз. Використовуйте цю інформацію, щоб визначити, чи$f$ є якісь точки перегину. Друга похідна також може бути використана як альтернативний засіб для визначення або перевірки того, що$f$ має локальний екстремум в критичній точці.

Тепер давайте використаємо цю стратегію для графіка декількох різних функцій. Почнемо з побудови графіка поліноміальної функції.

Приклад$\PageIndex{8}$: Sketching a Graph of a Polynomial

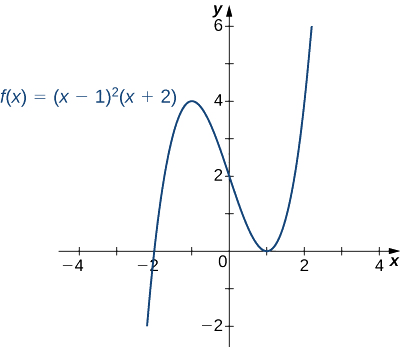
Намалюйте графік$f(x)=(x−1)^2(x+2).$

Рішення

Крок 1: Оскільки$f$ це многочлен, домен - це набір всіх дійсних чисел.

Крок 2: Коли$x=0,\; f(x)=2.$ Тому$y$ -перехоплення є$(0,2)$. Щоб знайти$x$ -перехоплення, нам потрібно вирішити рівняння$(x−1)^2(x+2)=0$, яке дає нам$x$ -перехоплення$(1,0)$ і$(−2,0)$

Крок 3: Нам потрібно оцінити кінцеву поведінку$f.$ As$x→∞, \;(x−1)^2→∞$ і$(x+2)→∞$. Тому,$\displaystyle \lim_{x→∞}f(x)=∞$.

Як$x→−∞, \;(x−1)^2→∞$ і$(x+2)→−∞$. Тому,$\displaystyle \lim_{x→-∞}f(x)=−∞$.

Щоб отримати ще більше інформації про кінцеву поведінку$f$, ми можемо помножити фактори$f$. Роблячи це, ми бачимо, що

\[f(x)=(x−1)^2(x+2)=x^3−3x+2. \nonumber \]

Оскільки провідним терміном$f$ є$x^3$, ми робимо висновок, що$f$ поводиться$y=x^3$ як$x→±∞.$

Крок 4: Оскільки$f$ є поліноміальною функцією, вона не має вертикальних асимптотів.

Крок 5: Перша похідна від$f$

\[f′(x)=3x^2−3. \nonumber \]

Тому$f$ має дві критичні точки:$x=1,−1.$$(−∞,∞)$ розділити інтервал на три менших інтервалу:$(−∞,−1), \;(−1,1)$, і$(1,∞)$. Потім вибирайте контрольні точки$x=−2, x=0$, а$x=2$ з цих інтервалів і оцініть знак$f′(x)$ на кожній з цих контрольних точок, як показано в наступній таблиці.

Інтервал	Тестовий пункт	Знак похідної$f'(x)=3x^2−3=3(x−1)(x+1)$	Висновок
$(−∞,−1)$	$x=−2$	\ (f' (x) =3x^2−3=3 (x−1) (x+1)\)» style="вирівнювання тексту: центр; ">$(+)(−)(−)=+$	$f$збільшується
$(−1,1)$	$x=0$	\ (f' (x) =3x^2−3=3 (x−1) (x+1)\)» style="вирівнювання тексту: центр; ">$(+)(−)(+)=−$	$f$зменшується
$(1,∞)$	$x=2$	\ (f' (x) =3x^2−3=3 (x−1) (x+1)\)» style="вирівнювання тексту: центр; ">$(+)(+)(+)=+$	$f$збільшується

З таблиці ми бачимо, що$f$ має локальний максимум at$x=−1$ і локальний мінімум на$x=1$. Оцінюючи$f(x)$ в цих двох точках, ми виявляємо, що локальне максимальне значення є,$f(−1)=4$ а локальне мінімальне значення є$f(1)=0.$

Крок 6: Друга$f$ похідна від

\[f''(x)=6x. \nonumber \]

Друга похідна дорівнює нулю в$x=0.$ Тому, щоб визначити увігнутість$f$,$(−∞,∞)$ розділити інтервал на менші інтервали$(−∞,0)$ і$(0,∞)$, і вибрати контрольні точки$x=−1$ і$x=1$ визначити увігнутість$f$ на кожному з цих менших інтервалів як показано в наступній таблиці.

Інтервал	Тестова точка	Знак$f''(x)=6x$	Висновок
$(−∞,0)$	$x=−1$	\ (f "(x) = 6x\)» style="вирівнювання тексту: центр; ">$−$	$f$увігнутий вниз.
$(0,∞)$	$x=1$	\ (f "(x) = 6x\)» style="вирівнювання тексту: центр; ">$+$	$f$увігнута вгору.

Відзначимо, що інформація в попередній таблиці підтверджує факт, виявлений в кроці$5$, що f має локальний максимум at$x=−1$ і локальний мінімум at$x=1$. Крім того, інформація, знайдена в кроці,$5$ а саме,$f$ має локальний максимум в$x=−1$ і локальний мінімум в$x=1$, і$f′(x)=0$ в цих точках - в поєднанні з тим, що знак$f''$ змін тільки на$x=0$ підтверджує результати, знайдені в кроці$6$ на увігнутість$f$.

Поєднуючи цю інформацію, ми приходимо до графіку,$f(x)=(x−1)^2(x+2)$ показаного на наступному графіку.

$Графічна функція f (x) = (x −1) 2 (x + 2). Він перетинає вісь x при x = −2 і торкається осі x при x = 1.$

Вправа$\PageIndex{8}$

Намалюйте графік$f(x)=(x−1)^3(x+2).$

Підказка: $f$є многочленом четвертого ступеня.
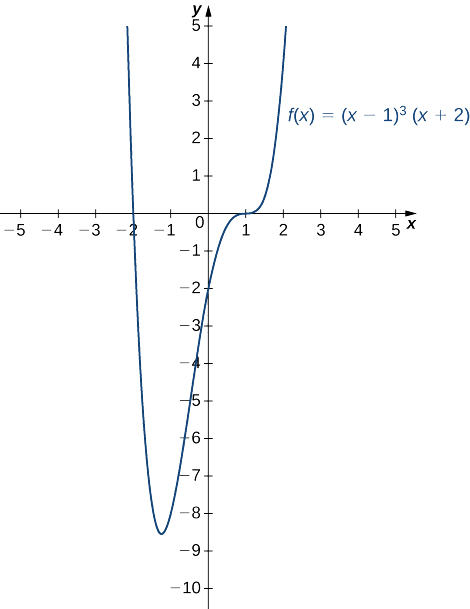
Відповідь: $Графічна функція f (x) = (x −1) 3 (x + 2).$

Приклад$\PageIndex{9}$: Sketching a Rational Function

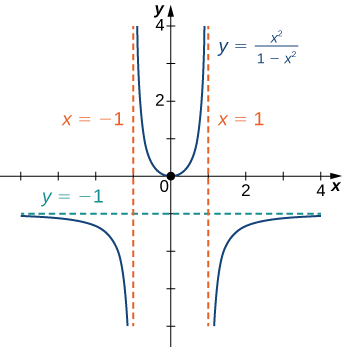
Намалюйте графік$f(x)=\dfrac{x^2}{1−x^2}$.

Рішення

Крок 1: Функція$f$ визначається до тих пір, поки знаменник не дорівнює нулю. Таким чином, домен являє собою набір всіх дійсних чисел,$x$ крім$x=±1.$

Крок 2: Знайдіть перехоплення. Якщо$x=0,$ тоді$f(x)=0$, так$0$ це перехоплення. Якщо$y=0$, то$\dfrac{x^2}{1−x^2}=0,$ що має на увазі$x=0$. Тому$(0,0)$ є єдиним перехопленням.

Крок 3: Оцініть межі на нескінченності. Оскільки$f$ є раціональною функцією, ділимо чисельник і знаменник на найвищу ступінь в знаменнику:$x^2$ .Отримуємо

$\displaystyle \lim_{x→±∞}\frac{x^2}{1−x^2}=\lim_{x→±∞}\frac{1}{\frac{1}{x^2}−1}=−1.$

Тому$f$ має горизонтальну асимптоту$y=−1$ як$x→∞$ і$x→−∞.$

Крок 4: Щоб визначити, чи$f$ має будь-які вертикальні асимптоти, спочатку перевірте, чи є у знаменника будь-які нулі. Знаходимо знаменник дорівнює нулю, коли$x=±1$. Щоб визначити, чи є лінії$x=1$ або$x=−1$ є вертикальними асимптотами$f$, оцінюють$\displaystyle \lim_{x→1}f(x)$ і$\displaystyle \lim_{x→−1}f(x)$. Дивлячись на кожну односторонню межу, як$x→1,$ ми бачимо, що

$\displaystyle \lim_{x→1^+}\frac{x^2}{1−x^2}=−∞$і$\displaystyle \lim_{x→1^−}\frac{x^2}{1−x^2}=∞.$

Крім того, дивлячись на кожну односторонню межу, коли ми$x→−1,$ виявляємо, що

$\displaystyle \lim_{x→−1^+}\frac{x^2}{1−x^2}=∞$і$\displaystyle \lim_{x→−1^−}\frac{x^2}{1−x^2}=−∞.$

Крок 5: Обчисліть першу похідну:

$f′(x)=\dfrac{(1−x^2)(2x)−x^2(−2x)}{\Big(1−x^2\Big)^2}=\dfrac{2x}{\Big(1−x^2\Big)^2}$.

Критичні точки виникають у точках$x$, де$f′(x)=0$ або$f′(x)$ не визначено. Ми бачимо, що$f′(x)=0$ коли$x=0.$ похідна не$f′$ є невизначеною в будь-якій точці в області$f$. Однак не$x=±1$ знаходяться в області$f$. Тому, щоб визначити, де$f$ збільшується, а де$f$ зменшується, розділіть інтервал$(−∞,∞)$ на чотири менші інтервали:$(−∞,−1), (−1,0), (0,1),$ і$(1,∞)$, і вибрати контрольну точку в кожному інтервалі, щоб визначити знак$f′(x)$ в кожному з цих інтервалів. Значення$x=−2,\; x=−\frac{1}{2}, \;x=\frac{1}{2}$, і$x=2$ є хорошим вибором для тестових точок, як показано в наступній таблиці.

Інтервал	Тестовий пункт	Знак$f′(x)=\frac{2x}{(1−x^2)^2}$	Висновок
$(−∞,−1)$	$x=−2$	\ (f′ (x) =\ розрив {2x} {(1−x^2) ^2}\)» стиль = "вирівнювання тексту: центр; ">$−/+=−$	$f$зменшується.
$(−1,0)$	$x=−1/2$	\ (f′ (x) =\ розрив {2x} {(1−x^2) ^2}\)» стиль = "вирівнювання тексту: центр; ">$−/+=−$	$f$зменшується.
$(0,1)$	$x=1/2$	\ (f′ (x) =\ розрив {2x} {(1−x^2) ^2}\)» стиль = "вирівнювання тексту: центр; ">$+/+=+$	$f$збільшується.
$(1,∞)$	$x=2$	\ (f′ (x) =\ розрив {2x} {(1−x^2) ^2}\)» стиль = "вирівнювання тексту: центр; ">$+/+=+$	$f$збільшується.

З цього аналізу ми робимо висновок, що$f$ має локальний мінімум,$x=0$ але не локальний максимум.

Крок 6: Обчисліть другу похідну:

\ [\ почати {вирівнювати*} f "(x) &=\ розрив {(1−x^2) ^2 (2) −2x (2 (1−x^2) (−2x))} {(1−x^2) ^4}\\ [4pt]
&=\ розрив {(1−x^2) [2 (1−x^2) +8x^2]} {\ Великий (1−x^2\ Великий) ^4}\\ [4pt]
&=\ розрив {2 (1−x^2) +8x^2} {\ Великий (1−х^2\ Великий) ^3}\\ [4pt]
&=\ розрив {6x^2+2} {\ Великий (1−х^2\ Великий) ^3}. \ end {вирівнювати*}\]

Щоб визначити інтервали, де$f$ увігнута вгору, а де$f$ увігнута вниз, нам спочатку потрібно знайти всі точки,$x$ де$f''(x)=0$ або$f''(x)$ є невизначеною. Так як чисельник$6x^2+2≠0$ для будь-якого ніколи не$x, f''(x)$ дорівнює нулю. Крім того, не$f''$ є невизначеною для будь-якого$x$ в області домену$f$. Однак, як обговорювалося раніше, не$x=±1$ знаходяться в області$f$. Тому, щоб визначити увігнутість$f$, ділимо інтервал на$(−∞,∞)$ три менші інтервали$(−∞,−1), \, (−1,1)$, причому$(1,∞)$, вибираємо контрольну точку в кожному з цих інтервалів, щоб оцінити знак$f''(x)$. Значення$x=−2, \;x=0$ і можливі$x=2$ контрольні точки, як показано в наступній таблиці.

Інтервал	Тестова точка	Знак$f''(x)=\frac{6x^2+2}{(1−x^2)^3}$	Висновок
$(−∞,−1)$	$x=−2$	\ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)» style="вирівнювання тексту: центр; ">$+/−=−$	$f$увігнутий вниз.
$(−1,1)$	$x=0$	\ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)» style="вирівнювання тексту: центр; ">$+/+=+$	$f$увігнута вгору
$(1,∞)$	$x=2$	\ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)» style="вирівнювання тексту: центр; ">$+/−=−$	$f$увігнутий вниз.

Об'єднавши всю цю інформацію, ми приходимо до графіку,$f$ показаного нижче. Зверніть увагу, що, хоча$f$ змінюється увігнутість при$x=−1$ і$x=1$, немає точок перегину ні в одному з цих місць, оскільки не$f$ є безперервним в$x=−1$ або$x=1.$

$Графік з 3 штук. Самий лівий починається вздовж горизонтальної асимптоти при Y дорівнює негативному 1 в лівій частині графіка і згинається до вертикальної асимптоти при X дорівнює негативному 1. Середній шматок смутно параболічний, падіння з верхньої частини графіка на X дорівнює негативному 1 до початку, а потім піднімається назад на вершину при X дорівнює 1. Третій шматок піднімається знизу при X дорівнює 1 і згинається, щоб досягти правої сторони уздовж горизонтальної асимптоти Y дорівнює негативному 1.$

Вправа$\PageIndex{9}$

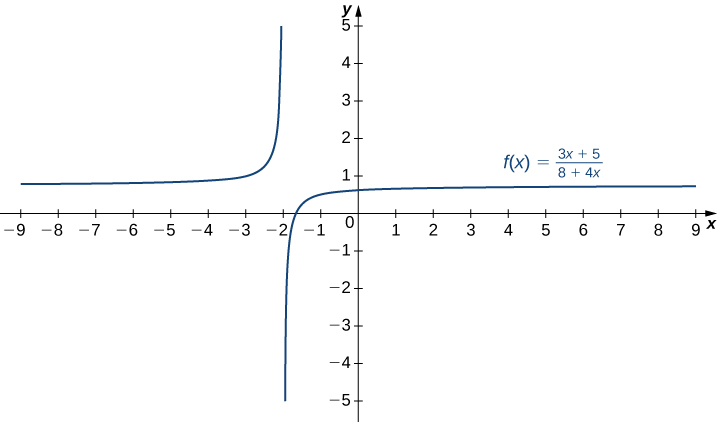
Намалюйте графік$f(x)=\dfrac{3x+5}{8+4x}.$

Підказка: Лінія$y=L$ - це горизонтальна асимптота,$f$ якщо межа як$x→∞$ або межа$x→−∞$ станом на$f(x)$ є$L$. Лінія$x=a$ - це вертикальна асимптота, якщо хоча б одна з односторонніх меж$f$ as$x→a$ є$∞$ або$−∞.$

Відповідь: $Функція f (x) = (3x + 5)/(8 + 4x) графічна. Здається, він має асимптоти при x = −2 та y = 1.$

Приклад$\PageIndex{10}$: Sketching a Rational Function with an Oblique Asymptote

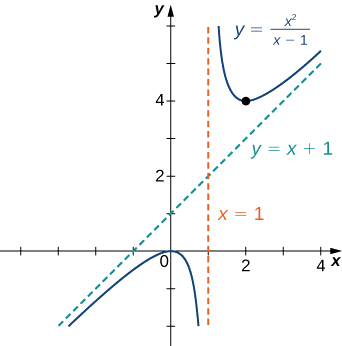
Намалюйте графік$f(x)=\dfrac{x^2}{x−1}$

Рішення

Крок 1: Домен$f$ - це набір всіх дійсних чисел,$x$ крім$x=1.$

Крок 2: Знайдіть перехоплення. Ми бачимо, що коли$x=0, \,f(x)=0,$ так$(0,0)$ є єдиним перехопленням.

Крок 3: Оцініть межі на нескінченності. Так як ступінь чисельника на один більше ступеня знаменника,$f$ повинна мати косу асимптоту. Щоб знайти косу асимптоту, використовуйте довге ділення многочленів для запису

$f(x)=\dfrac{x^2}{x−1}=x+1+\dfrac{1}{x−1}$.

Оскільки$\dfrac{1}{x−1}→0$ як$x→±∞, f(x)$ наближається до лінії$y=x+1$ як$x→±∞$. Лінія$y=x+1$ - коса асимптота для$f$.

Крок 4: Щоб перевірити наявність вертикальних асимптотів, подивіться, де знаменник дорівнює нулю. Тут знаменник дорівнює нулю на$x=1.$ Дивлячись на обидві односторонні межі, як$x→1,$ ми знаходимо

$\displaystyle \lim_{x→1^+}\frac{x^2}{x−1}=∞$і$\displaystyle \lim_{x→1^−}\frac{x^2}{x−1}=−∞.$

Отже,$x=1$ це вертикальна асимптота, і ми визначили поведінку$f$ як$x$ підходів$1$ праворуч, так і зліва.

Крок 5: Обчисліть першу похідну:

$f′(x)=\dfrac{(x−1)(2x)−x^2(1)}{(x−1)^2}=\dfrac{x^2−2x}{(x−1)^2}.$

У нас є$f′(x)=0$ коли$x^2−2x=x(x−2)=0$. Тому$x=0$ і$x=2$ є критичними моментами. Оскільки$f$ не визначено в$x=1$, нам потрібно$(−∞,∞)$ розділити інтервал на менші інтервали$(−∞,0), (0,1), (1,2),$ і$(2,∞)$, і вибрати контрольну точку з кожного інтервалу, щоб оцінити знак$f′(x)$ в кожному з цих менших інтервалів. Наприклад, нехай$x=−1, x=\frac{1}{2}, x=\frac{3}{2}$, і$x=3$ бути контрольними точками, як показано в наступній таблиці.

Інтервал	Тестова точка	Знак$f'(x)=\dfrac{x^2−2x}{(x−1)^2}$	Висновок
$(−∞,0)$	$x=−1$	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)» перевірка даних = «верхня"> (−) (−) /+=+	$f$збільшується.
$(0,1)$	$x=1/2$	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)» перевірка даних ="верх"> (+) (−) /+=−	$f$зменшується.
$(1,2)$	$x=3/2$	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)» перевірка даних ="верх"> (+) (−) /+=−	$f$зменшується.
$(2,∞)$	$x=3$	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)» перевірка даних = «верхня"> (+) (+) /+=+	$f$збільшується.

З цієї таблиці ми бачимо, що$f$ має локальний максимум at$x=0$ і локальний мінімум на$x=2$. Значення$f$ при локальному максимумі є,$f(0)=0$ а значення$f$ при локальному мінімумі дорівнює$f(2)=4$. Тому$(0,0)$ і$(2,4)$ є важливими пунктами на графіку.

Крок 6. Обчисліть другу похідну:

\ [\ begin {align*} f "(x) &=\ розрив {(x−1) ^2 (2x−2) −2 (x−1) (x^2−2x)} {(x−1) ^4}\\ [4pt]
&=\ frac {2 (x−1) [(x−1) ^2− (x^2−2x)] {(x−1) ^4}\\ [4pt]
&=\ розрив {2 [x^2-2x+1−x^2x]} {(x−1) ^3}\\ [4pt]
&=\ розрив {2} {(x−1) ^3}. \ end {вирівнювати*}\]

Ми бачимо,$f''(x)$ що ніколи не нуль або невизначений для$x$ в області$f$. Оскільки$f$ не визначено в$x=1$, для перевірки$(−∞,∞)$ увігнутості ми просто ділимо інтервал на два менші інтервали$(−∞,1)$ і$(1,∞)$, і вибираємо контрольну точку з кожного інтервалу, щоб оцінити знак$f''(x)$ в кожному з цих інтервалів. Значення$x=0$ і$x=2$ можливі контрольні точки, як показано в наступній таблиці.

Інтервал	Тестова точка	Знак$f''(x)=\dfrac{2}{(x−1)^3}$	Висновок
$(−∞,1)$	$x=0$	\ (f "(x) =\ dfrac {2} {(x−1) ^3}\)» style="вирівнювання тексту: центр; ">$+/−=−$	$f$увігнутий вниз.
$(1,∞)$	$x=2$	\ (f "(x) =\ dfrac {2} {(x−1) ^3}\)» style="вирівнювання тексту: центр; ">$+/+=+$	$f$увігнута вгору

З зібраної інформації ми приходимо до наступного графіка для$f.$

$Графічна функція f (x) = x2/ (x − 1). Він має асимптоти y = х + 1 і х = 1.$

Вправа$\PageIndex{10}$

Знайти косу асимптоту для$f(x)=\dfrac{3x^3−2x+1}{2x^2−4}$.

Підказка: Використовуйте довге ділення многочленів.

Відповідь: $y=\frac{3}{2}x$

Приклад$\PageIndex{11}$: Sketching the Graph of a Function with a Cusp

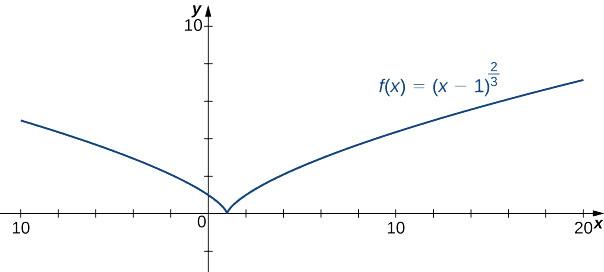
Намалюйте графік$f(x)=(x−1)^{2/3}$

Рішення

Крок 1: Оскільки функція cube-root визначена для всіх дійсних чисел$x$ і$(x−1)^{2/3}=(\sqrt[3]{x−1})^2$, область всіх$f$ дійсних чисел.

Крок 2: Щоб знайти$y$ -перехоплення, оцініть$f(0)$. Так як$f(0)=1,$$y$ -перехоплення є$(0,1)$. Щоб знайти$x$ -перехоплення, вирішуйте$(x−1)^{2/3}=0$. Рішення цього рівняння є$x=1$, тому$x$ -перехоплення$(1,0).$

Крок 3: Оскільки$\displaystyle \lim_{x→±∞}(x−1)^{2/3}=∞,$ функція продовжує рости без прив'язки як$x→∞$ і$x→−∞.$

Крок 4: Функція не має вертикальних асимптотів.

Крок 5: Щоб визначити, де$f$ збільшується або зменшується,$f′.$ обчислюємо Знаходимо

\[f′(x)=\frac{2}{3}(x−1)^{−1/3}=\frac{2}{3(x−1)^{1/3}} \nonumber \]

Ця функція ніде не дорівнює нулю, але вона не визначена, коли$x=1.$ Тому єдиною критичною точкою є$x=1.$$(−∞,∞)$ Розділити інтервал на менші інтервали$(−∞,1)$ і$(1,∞)$, і вибрати контрольні точки в кожному з цих інтервалів, щоб визначити знак$f′(x)$ в кожному з них менші інтервали. $x=0$$x=2$Дозволяти і бути контрольними точками, як показано в наступній таблиці.

Інтервал	Тестова точка	Знак$f′(x)=\frac{2}{3(x−1)^{1/3}}$	Висновок
$(−∞,1)$	$x=0$	\ (f′ (x) =\ розрив {2} {3 (x−1) ^ {1/3}}\)» style="вирівнювання тексту: центр; ">$+/−=−$	$f$зменшується
$(1,∞)$	$x=2$	\ (f′ (x) =\ розрив {2} {3 (x−1) ^ {1/3}}\)» style="вирівнювання тексту: центр; ">$+/+=+$	$f$збільшується

Робимо висновок, що$f$ має локальний мінімум при$x=1$. Оцінюючи$f$ при$x=1$, ми виявимо, що значення$f$ при локальному мінімумі дорівнює нулю. Зверніть увагу,$f′(1)$ що не визначено, тому, щоб визначити поведінку функції в цій критичній точці, нам потрібно вивчити$\displaystyle \lim_{x→1}f′(x).$ Дивлячись на односторонні межі, ми маємо

\[\lim_{x→1^+}\frac{2}{3(x−1)^{1/3}}=∞\text{ and } \lim_{x→1^−}\frac{2}{3(x−1)^{1/3}}=−∞.\nonumber \]

Тому$f$ має поглиблення при$x=1.$

Крок 6: Для визначення увігнутості обчислюємо другу похідну$f:$

\[f''(x)=−\dfrac{2}{9}(x−1)^{−4/3}=\dfrac{−2}{9(x−1)^{4/3}}. \nonumber \]

Ми знаходимо,$f''(x)$ що визначено для всіх$x$, але не визначено, коли$x=1$. Тому розділіть інтервал$(−∞,∞)$ на менші інтервали$(−∞,1)$ і$(1,∞)$, і вибирайте контрольні точки для оцінки знака$f''(x)$ в кожному з цих інтервалів. Як ми робили раніше, нехай$x=0$ і$x=2$ бути тестовими точками, як показано в наступній таблиці.

Інтервал	Тестова точка	Знак$f''(x)=\dfrac{−2}{9(x−1)^{4/3}}$	Висновок
$(−∞,1)$	$x=0$	\ (f "(x) =\ dfrac {−2} {9 (x−1) ^ {4/3}}\)» style="вирівнювання тексту: центр; ">$−/+=−$	$f$увігнутий вниз
$(1,∞)$	$x=2$	\ (f "(x) =\ dfrac {−2} {9 (x−1) ^ {4/3}}\)» style="вирівнювання тексту: центр; ">$−/+=−$	$f$увігнутий вниз

З цієї таблиці робимо висновок,$f$ що увігнута вниз всюди. Об'єднавши всю цю інформацію, ми приходимо до наступного графіку для$f$.

$Графічна функція f (x) = (x − 1) 2/3. Він торкається осі х при x = 1, де справа доходить до чогось гострої точки, а потім вилітає з обох сторін.$

Вправа$\PageIndex{11}$

Розглянемо функцію$f(x)=5−x^{2/3}$. Визначте точку на графіку, де знаходиться перехрестя. Визначте кінцеву поведінку$f$.

Підказка: Функція$f$ має куп у точці,$a$ якщо$f(a)$$f'(a)$ існує, не визначена, одна з односторонніх обмежень$x→a$ станом на$f'(x)$ є$+∞$, а інша одностороння межа$−∞.$

Відповідь: Функція$f$ має cusp at$(0,5)$, так як$\displaystyle \lim_{x→0^−}f′(x)=∞$ і$\displaystyle \lim_{x→0^+}f′(x)=−∞$. Для кінцевої поведінки,$\displaystyle \lim_{x→±∞}f(x)=−∞.$

Ключові концепції

Межа$f(x)$ є$L$ як$x→∞$ (або як$x→−∞)$ ніби значення$f(x)$ стають довільно близькими до того$L$, як$x$ стає досить великим.
Межа$f(x)$ є$∞$ як$x→∞$ би$f(x)$ стає довільно великим, оскільки$x$ стає досить великим. Межа$f(x)$ є$−∞$$x→∞$ ніби$f(x)<0$ і$|f(x)|$ стає довільно великим, оскільки$x$ стає досить великим. Ми можемо визначити межу$f(x)$ як$x$ підходів$−∞$ аналогічно.
Для поліноміальної функції$p(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0,$ де$a_n≠0$, кінцева поведінка визначається провідним терміном$a_nx^n$. Якщо$n≠0, p(x)$ наближається$∞$ або$−∞$ на кожному кінці.
Для$f(x)=\dfrac{p(x)}{q(x),}$ раціональної функції кінцева поведінка визначається залежністю між ступенем$p$ і ступенем$q$. Якщо ступінь менше ступеня$p$$q$, то лінія$y=0$ є горизонтальною асимптотою для$f$. Якщо ступінь$p$ дорівнює градусу$q$, то лінія$y=\dfrac{a_n}{b_n}$ являє собою горизонтальну асимптоту, де$a_n$ і$b_n$ є провідними коефіцієнтами$p$ і$q$, відповідно. Якщо ступінь$p$ більше ступеня$q$, то$f$ підходить$∞$ або$−∞$ на кожному кінці.

Глосарій

кінець поведінка: поведінка функції як$x→∞$ і$x→−∞$

горизонтальна асимптота: якщо$\displaystyle \lim_{x→∞}f(x)=L$ або$\displaystyle \lim_{x→−∞}f(x)=L$, то$y=L$ є горизонтальним асимптотом$f$

нескінченна межа на нескін: функція, яка стає довільно великий, як$x$ стає великим

межа на нескінченність: функція, яка наближається до граничного значення$L$, як$x$ стає великим

коса асимптота: лінія,$y=mx+b$ якщо$f(x)$ наближається до неї як$x→∞$ або$ x→−∞$

Інтервал	Тестовий пункт	Знак похідної\(f'(x)=3x^2−3=3(x−1)(x+1)\)	Висновок
\((−∞,−1)\)	\(x=−2\)	\ (f' (x) =3x^2−3=3 (x−1) (x+1)\)» style="вирівнювання тексту: центр; ">\((+)(−)(−)=+\)	\(f\)збільшується
\((−1,1)\)	\(x=0\)	\ (f' (x) =3x^2−3=3 (x−1) (x+1)\)» style="вирівнювання тексту: центр; ">\((+)(−)(+)=−\)	\(f\)зменшується
\((1,∞)\)	\(x=2\)	\ (f' (x) =3x^2−3=3 (x−1) (x+1)\)» style="вирівнювання тексту: центр; ">\((+)(+)(+)=+\)	\(f\)збільшується

Інтервал	Тестова точка	Знак\(f''(x)=6x\)	Висновок
\((−∞,0)\)	\(x=−1\)	\ (f "(x) = 6x\)» style="вирівнювання тексту: центр; ">\(−\)	\(f\)увігнутий вниз.
\((0,∞)\)	\(x=1\)	\ (f "(x) = 6x\)» style="вирівнювання тексту: центр; ">\(+\)	\(f\)увігнута вгору.

Інтервал	Тестовий пункт	Знак\(f′(x)=\frac{2x}{(1−x^2)^2}\)	Висновок
\((−∞,−1)\)	\(x=−2\)	\ (f′ (x) =\ розрив {2x} {(1−x^2) ^2}\)» стиль = "вирівнювання тексту: центр; ">\(−/+=−\)	\(f\)зменшується.
\((−1,0)\)	\(x=−1/2\)	\ (f′ (x) =\ розрив {2x} {(1−x^2) ^2}\)» стиль = "вирівнювання тексту: центр; ">\(−/+=−\)	\(f\)зменшується.
\((0,1)\)	\(x=1/2\)	\ (f′ (x) =\ розрив {2x} {(1−x^2) ^2}\)» стиль = "вирівнювання тексту: центр; ">\(+/+=+\)	\(f\)збільшується.
\((1,∞)\)	\(x=2\)	\ (f′ (x) =\ розрив {2x} {(1−x^2) ^2}\)» стиль = "вирівнювання тексту: центр; ">\(+/+=+\)	\(f\)збільшується.

Інтервал	Тестова точка	Знак\(f''(x)=\frac{6x^2+2}{(1−x^2)^3}\)	Висновок
\((−∞,−1)\)	\(x=−2\)	\ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)» style="вирівнювання тексту: центр; ">\(+/−=−\)	\(f\)увігнутий вниз.
\((−1,1)\)	\(x=0\)	\ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)» style="вирівнювання тексту: центр; ">\(+/+=+\)	\(f\)увігнута вгору
\((1,∞)\)	\(x=2\)	\ (f "(x) =\ frac {6x^2+2} {(1−x^2) ^3}\)» style="вирівнювання тексту: центр; ">\(+/−=−\)	\(f\)увігнутий вниз.

Інтервал	Тестова точка	Знак\(f'(x)=\dfrac{x^2−2x}{(x−1)^2}\)	Висновок
\((−∞,0)\)	\(x=−1\)	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)» перевірка даних = «верхня"> (−) (−) /+=+	\(f\)збільшується.
\((0,1)\)	\(x=1/2\)	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)» перевірка даних ="верх"> (+) (−) /+=−	\(f\)зменшується.
\((1,2)\)	\(x=3/2\)	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)» перевірка даних ="верх"> (+) (−) /+=−	\(f\)зменшується.
\((2,∞)\)	\(x=3\)	\ (f' (x) =\ dfrac {x^2−2x} {(x−1) ^2}\)» перевірка даних = «верхня"> (+) (+) /+=+	\(f\)збільшується.

Визначення: Межа на нескінченність (неформальна)

Визначення: Горизонтальна асимптота

Приклад\(\PageIndex{1}\): Computing Limits at Infinity

Вправа\(\PageIndex{1}\)

Визначення: Нескінченна межа і нескінченність (неформа

Визначення: Межа на нескінченність (формальна)

Приклад\(\PageIndex{2}\):

Вправа\(\PageIndex{2}\)

Визначення: Нескінченна межа і нескінченність (формальна

Приклад\(\PageIndex{3}\)

Вправа\(\PageIndex{3}\)

Приклад\(\PageIndex{4}\): Limits at Infinity for Power Functions

Вправа\(\PageIndex{4}\)

Приклад\(\PageIndex{5}\): Determining End Behavior for Rational Functions

Вправа\(\PageIndex{5}\)

Приклад\(\PageIndex{6}\): Determining End Behavior for a Function Involving a Radical

Вправа\(\PageIndex{6}\)

Приклад\(\PageIndex{7}\): Determining End Behavior for a Transcendental Function

Вправа\(\PageIndex{7}\)

Стратегія вирішення проблем: креслення графіка функції

Приклад\(\PageIndex{8}\): Sketching a Graph of a Polynomial

Вправа\(\PageIndex{8}\)

Приклад\(\PageIndex{9}\): Sketching a Rational Function

Вправа\(\PageIndex{9}\)

Приклад\(\PageIndex{10}\): Sketching a Rational Function with an Oblique Asymptote

Вправа\(\PageIndex{10}\)

Приклад\(\PageIndex{11}\): Sketching the Graph of a Function with a Cusp

Вправа\(\PageIndex{11}\)

\(x\)	10	100	1 000	10 000
\(2+\frac{1}{x}\)	2.1	2.01	2.001	2.0001
\(x\)	−10	−100	−1000	−10 000
\(2+\frac{1}{x}\)	1.9	1,99	1.999	1.999

\(x\)	10	20	50	100	1000
\(x^3\)	1000	8000	125 000	1 000 000	1 000 000 000
\(x\)	−10	−20	−50	−100	−1000
\(x^3\)	−1000	−8000	−125 000	−1 000 000	−1 000 000 000

\(x\)	10	100	1000
\(f(x)=5x^3−3x^2+4\)	4704	4 970 004	4 997 000 004
\(g(x)=5x^3\)	5000	5 000 000	5 000 000 000
\(x\)	−10	−100	−000
\(f(x)=5x^3−3x^2+4\)	−5296	−5 029 996	−5 002 999 996
\(g(x)=5x^3\)	−5000	−5 000 000	−5 000 000 000

Інтервал	Тестова точка	Знак\(f''(x)=\dfrac{2}{(x−1)^3}\)	Висновок
\((−∞,1)\)	\(x=0\)	\ (f "(x) =\ dfrac {2} {(x−1) ^3}\)» style="вирівнювання тексту: центр; ">\(+/−=−\)	\(f\)увігнутий вниз.
\((1,∞)\)	\(x=2\)	\ (f "(x) =\ dfrac {2} {(x−1) ^3}\)» style="вирівнювання тексту: центр; ">\(+/+=+\)	\(f\)увігнута вгору