4.7: Прикладні проблеми оптимізації

Цілі навчання

• Налаштуйте та вирішуйте задачі оптимізації в декількох прикладних областях.

Одним із поширених застосувань обчислення є обчислення мінімального або максимального значення функції. Наприклад, компанії часто хочуть мінімізувати виробничі витрати або максимізувати дохід. При виготовленні часто бажано мінімізувати кількість матеріалу, що використовується для упаковки продукту з певним обсягом. У цьому розділі ми покажемо, як налаштувати ці типи проблем мінімізації та максимізації та вирішити їх за допомогою інструментів, розроблених у цьому розділі.

Розв'язування задач оптимізації за замкнутий обмежений інтервал

Основна ідея проблем оптимізації, які слідують, однакова. У нас є певна кількість, яку ми зацікавлені в максимізації або мінімізації. Однак у нас також є якась допоміжна умова, яку потрібно задовольнити. Наприклад, в прикладі ми зацікавлені в тому$\PageIndex{1}$, щоб максимально збільшити площу прямокутного саду. Звичайно, якщо ми продовжуємо робити бічні довжини саду більшими, площа буде продовжувати ставати більшою. Однак що робити, якщо у нас є деяке обмеження щодо того, скільки огорожі ми можемо використовувати для периметра? У цьому випадку ми не можемо зробити сад таким великим, як нам подобається. Давайте розглянемо, як ми можемо максимізувати площу прямокутника з урахуванням деяких обмежень по периметру.

Приклад$\PageIndex{1}$: Maximizing the Area of a Garden

Прямокутний сад повинен бути побудований з використанням кам'яної стіни в якості однієї сторони саду і дротяної огорожі для інших трьох сторін (рис.$\PageIndex{1}$). Враховуючи$100\,\text{ft}$ дротяні огорожі, визначте розміри, які б створювали сад максимальної площі. Яка максимальна площа?

Малюнок$\PageIndex{1}$: Ми хочемо визначити виміри$x$ і$y$ що дозволить створити сад з максимальною площею$100\,\text{ft}$ використання огорожі.

Рішення

Нехай$x$ позначимо довжину сторони саду перпендикулярно кам'яній стіні і$y$ позначимо довжину сторони, паралельної кам'яній стіні. Тоді площа саду становить

$A=x⋅y.$

Ми хочемо знайти максимально можливу площу з урахуванням обмеження, що загальна огорожа$100\,\text{ft}$. З$\PageIndex{1}$ малюнка загальна кількість використовуваної огорожі буде$2x+y.$ Таким чином, рівняння обмеження є

$2x+y=100.$

Вирішуючи це рівняння для$y$, ми маємо$y=100−2x.$ Таким чином, ми можемо записати область як

$A(x)=x⋅(100−2x)=100x−2x^2.$

Перш ніж намагатися максимізувати функцію області,$A(x)=100x−2x^2,$ нам потрібно визначити розглянутий домен. Щоб побудувати прямокутний сад, нам, безумовно, потрібні довжини обох сторін, щоб бути позитивними. Тому нам$x>0$ і потрібно$y>0$. Так як$y=100−2x$, якщо$y>0$, то$x<50$. Тому намагаємося визначити максимальне значення$A(x)$ for$x$ за відкритий інтервал$(0,50)$. Ми не знаємо, що функція обов'язково має максимальне значення протягом відкритого інтервалу. Однак ми знаємо, що безперервна функція має абсолютний максимум (і абсолютний мінімум) протягом замкнутого інтервалу. Тому розглянемо функцію$A(x)=100x−2x^2$ за замкнутим інтервалом$[0,50]$. Якщо максимальне значення відбувається у внутрішній точці, то ми знайшли значення$x$ у відкритому інтервалі$(0,50)$, яке максимізує площу саду.

Тому розглянемо наступну проблему:

Максимізувати$A(x)=100x−2x^2$ протягом інтервалу$[0,50].$

Як вже говорилося раніше, оскільки$A$ є неперервною функцією на замкнутому обмеженому інтервалі, за теоремою крайніх значень вона має максимум і мінімум. Ці крайні значення виникають або в кінцевих точках, або в критичних точках. У кінцевих точках,$A(x)=0$. Так як площа позитивна для всіх$x$ у відкритому проміжку$(0,50)$, максимум повинен відбуватися в критичній точці. Диференціюючи функцію$A(x)$, отримаємо

$A′(x)=100−4x.$

Тому єдиною критичною точкою є$x=25$ (рис.$\PageIndex{2}$). Робимо висновок, що максимальна площа повинна відбуватися при$x=25$.

Малюнок$\PageIndex{2}$: Щоб максимально збільшити площу саду, нам потрібно знайти максимальне значення функції$A(x)=100x−2x^2$.

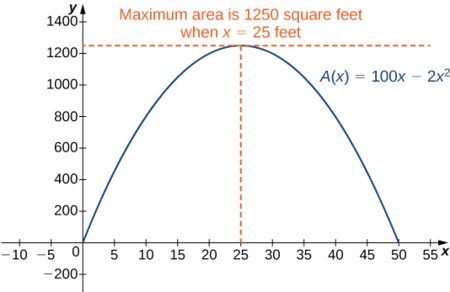
Тоді ми повинні максимально$y=100−2x=100−2(25)=50.$ збільшити площу саду, нехай$x=25\,\text{ft}$ і$y=50\,\text{ft}$. Площа цього саду становить$1250\, \text{ft}^2$.

Вправа$\PageIndex{1}$

Визначте максимальну площу, якщо ми хочемо зробити такий же прямокутний сад, як на малюнку$\PageIndex{2}$, але у нас є$200\,\text{ft}$ огорожі.

Підказка

Нам потрібно максимізувати функцію$A(x)=200x−2x^2$ за інтервал$[0,100].$

Відповідь

Максимальна площа -$5000\, \text{ft}^2$.

Тепер розглянемо загальну стратегію вирішення задач оптимізації, подібну до Example$\PageIndex{1}$.

Стратегія вирішення проблем: рішення задач оптимізації

1. Ввести всі змінні. Якщо це можливо, намалюйте фігуру та позначте всі змінні.
2. Визначте, яку величину потрібно максимізувати або звести до мінімуму, і для якого діапазону значень інших змінних (якщо це можна визначити в цей час).
3. Напишіть формулу для величини, яку потрібно максимізувати або звести до мінімуму через змінні. Ця формула може включати більше однієї змінної.
4. Запишіть будь-які рівняння, що стосуються незалежних змінних, у формулу з кроку$3$. Використовуйте ці рівняння, щоб записати величину, яку потрібно максимізувати або мінімізувати як функцію однієї змінної.
5. Визначте область розгляду функції поетапно на$4$ основі фізичної проблеми, яку потрібно вирішити.
6. Знайдіть максимальне або мінімальне значення функції з кроку$4.$ Цей крок зазвичай передбачає пошук критичних точок та оцінку функції в кінцевих точках.

Тепер давайте застосуємо цю стратегію, щоб максимізувати об'єм коробки з відкритим верхом, враховуючи обмеження на кількість використовуваного матеріалу.

Приклад$\PageIndex{2}$: Maximizing the Volume of a Box

Коробка з відкритим верхом повинна бути зроблена з$24\,\text{in.}$ по$36\,\text{in.}$ шматочку картону, видаливши квадрат з кожного кута коробки і склавши стулки з кожного боку. Якого розміру квадрат потрібно вирізати з кожного кута, щоб вийшла коробка з максимальним обсягом?

Рішення

Крок 1:$x$ Дозволяти довжину сторони квадрата, який потрібно видалити з кожного кута (рис.$\PageIndex{3}$). Потім решта чотири стулки можна скласти, щоб утворити коробку з відкритим верхом. $V$Дозволяти буде обсяг отриманої коробки.

Малюнок$\PageIndex{3}$: З кожного кута шматка картону знімається квадрат з довжиною сторони$x$ дюймів. Решта стулки складають, щоб утворилася коробка з відкритим верхом.

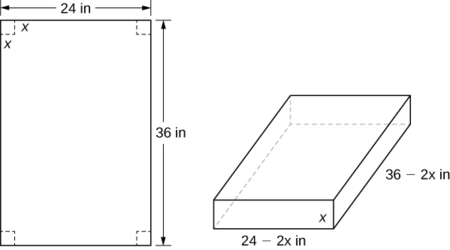
Крок 2: Намагаємося максимально збільшити обсяг коробки. Тому проблема полягає в тому, щоб максимізувати$V$.

Крок 3: Як згадувалося на кроці 2, намагаємося максимально збільшити об'єм коробки. Обсяг коробки дорівнює

$$V=L⋅W⋅H \nonumber, \nonumber$$

де$L,\,W,$$H$ і - довжина, ширина і висота відповідно.

Крок 4: З малюнка ми бачимо$\PageIndex{3}$, що висота коробки -$x$ дюйми, довжина -$36−2x$ дюйми, а ширина -$24−2x$ дюйми. Тому обсяг коробки дорівнює

$$\begin{align*} V(x) &=(36−2x)(24−2x)x \\[4pt] &=4x^3−120x^2+864x \end{align*}. \nonumber$$

Крок 5: Щоб визначити область розгляду, розглянемо рисунок$\PageIndex{3}$. Звичайно, нам потрібно$x>0.$ Крім того, довжина сторони квадрата не може бути більшою або рівною половині довжини коротшої сторони$24\,\text{in.}$; інакше одна з стулок буде повністю відрізана. Тому ми намагаємося визначити, чи є максимальний обсяг коробки для$x$ протягом відкритого інтервалу$(0,12).$ Оскільки$V$ є безперервною функцією над замкнутим інтервалом$[0,12]$, ми знаємо, що$V$ буде мати абсолютний максимум за замкнутий інтервал. Тому розглядаємо$V$ над замкнутим інтервалом$[0,12]$ і перевіряємо, чи виникає абсолютний максимум у внутрішній точці.

Крок 6: Оскільки$V(x)$ є безперервною функцією над замкнутим, обмеженим інтервалом$[0,12]$,$V$ повинен мати абсолютний максимум (і абсолютний мінімум). Так як$V(x)=0$ в кінцевих точках і$V(x)>0$$0<x<12,$ по максимуму повинна відбуватися критична точка. Похідна - це

$V′(x)=12x^2−240x+864.$

Щоб знайти критичні точки, нам потрібно вирішити рівняння

$12x^2−240x+864=0.$

Розділивши обидві сторони цього рівняння на$12$, задача спрощує розв'язування рівняння

$x^2−20x+72=0.$

Використовуючи квадратичну формулу, знаходимо, що критичні точки

$$\begin{align*} x &=\dfrac{20±\sqrt{(−20)^2−4(1)(72)}}{2} \\[4pt] &=\dfrac{20±\sqrt{112}}{2} \\[4pt] &=\dfrac{20±4\sqrt{7}}{2} \\[4pt] &=10±2\sqrt{7} \end{align*}. \nonumber$$

Оскільки$10+2\sqrt{7}$ це не в області розгляду, єдиним критичним моментом, який нам потрібно врахувати, є$10−2\sqrt{7}$. Тому гучність максимізується, якщо ми дозволимо$x=10−2\sqrt{7}\,\text{in.}$ Максимальна гучність

$$V(10−2\sqrt{7})=640+448\sqrt{7}≈1825\,\text{in}^3. \nonumber$$

як показано на наступному графіку.

Малюнок$\PageIndex{4}$: Максимізація об'єму коробки призводить до знаходження максимального значення кубічного многочлена.

Вправа$\PageIndex{2}$

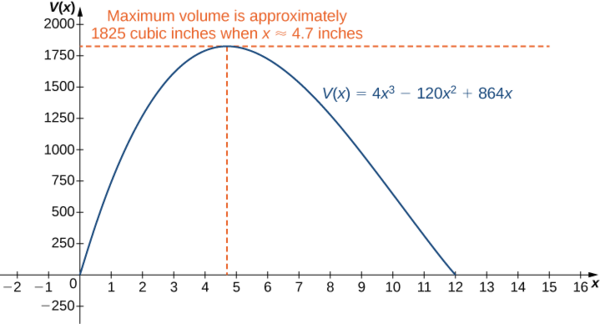
Припустимо, розміри картону в прикладі$\PageIndex{2}$ є$20\,\text{in.}$$30\,\text{in.}$$x$ Дозволяти бути довжиною сторони кожного квадрата і запишіть обсяг коробки з відкритим верхом як функцію$x$. Визначте область розгляду для$x$.

Підказка

Обсяг коробки дорівнює$L⋅W⋅H.$

Відповідь

$V(x)=x(20−2x)(30−2x).$Домен є$[0,10]$.

Приклад$\PageIndex{3}$: Minimizing Travel Time

Острів$2$ mi через північ від найближчої точки вздовж прямої берегової лінії. Відвідувач зупиняється в будиночку на березі, яка знаходиться$6$ милі на захід від цієї точки. Відвідувач планує відправитися з каюти на острів. Припустимо, відвідувач біжить зі швидкістю$8$ миль/год і плаває зі швидкістю$3$ миль/год. Як далеко відвідувач повинен бігти перед купанням, щоб мінімізувати час, необхідний для досягнення острова?

Рішення

Крок 1:$x$ Дозволяти дистанції бігу і нехай$y$ буде дистанція плавання (рис.$\PageIndex{5}$). Нехай$T$ буде час, необхідний для того, щоб дістатися з каюти на острів.

Малюнок$\PageIndex{5}$: Як ми можемо$y$ вибрати$x$ і мінімізувати час у дорозі від салону до острова?

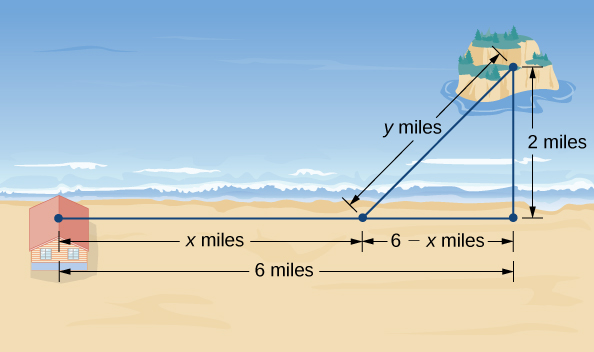
Крок 2: Проблема полягає в мінімізації$T$.

Крок 3: Щоб знайти час, витрачений на подорож з салону на острів, додайте час, проведений біг і час, витрачений на плавання. Оскільки відстань = швидкість × час час$(D=R×T),$, витрачений на біг

$T_{running}=\dfrac{D_{running}}{R_{running}}=\dfrac{x}{8}$,

і час, проведений плавання,

$T_{swimming}=\dfrac{D_{swimming}}{R_{swimming}}=\dfrac{y}{3}$.

Тому загальний час, проведений на подорожі, становить

$T=\dfrac{x}{8}+\dfrac{y}{3}$.

Крок 4: З малюнка$\PageIndex{5}$ відрізок лінії$y$ миль утворює гіпотенузу прямокутного трикутника з катетами довжини$2$ mi і$6−x$ mi. Тому за теоремою Піфагора$2^2+(6−x)^2=y^2$, і отримаємо$y=\sqrt{(6−x)^2+4}$. Таким чином, загальний час, проведений в подорожі, задається функцією

$T(x)=\dfrac{x}{8}+\dfrac{\sqrt{(6−x)^2+4}}{3}$.

Крок 5: З малюнка ми бачимо$\PageIndex{5}$, що$0≤x≤6$. Тому$[0,6]$ є сферою розгляду.

Крок 6: Оскільки$T(x)$ є безперервною функцією протягом замкнутого обмеженого інтервалу, вона має максимум і мінімум. Почнемо з пошуку будь-яких критичних точок$T$ над інтервалом$[0,6].$ Похідна є

$$\begin{align*} T′(x) &=\dfrac{1}{8}−\dfrac{1}{2}\dfrac{[(6−x)^2+4]^{−1/2}}{3}⋅2(6−x) \\[4pt] &=\dfrac{1}{8}−\dfrac{(6−x)}{3\sqrt{(6−x)^2+4}} \end{align*}$$

Якщо$T′(x)=0,$, то

$$\dfrac{1}{8}=\dfrac{6−x}{3\sqrt{(6−x)^2+4}} \label{ex3eq1}$$

Тому,

$$3\sqrt{(6−x)^2+4}=8(6−x). \label{ex3eq2}$$

Квадратуючи обидві сторони цього рівняння, ми бачимо, що якщо$x$ задовольняє це рівняння, то$x$ повинні задовольнити

$$9[(6−x)^2+4]=64(6−x)^2,\nonumber$$

що має на увазі

$$55(6−x)^2=36. \nonumber$$

Робимо висновок,$x$ що якщо критична точка, то$x$ задовольняє

$$(x−6)^2=\dfrac{36}{55}. \nonumber$$

[Зверніть увагу, що так як ми квадрат,$(x-6)^2 = (6-x)^2.$]

Тому можливості для критичних точок є

$$x=6±\dfrac{6}{\sqrt{55}}.\nonumber$$

Оскільки він не$x=6+6/\sqrt{55}$ знаходиться в домені, це не можливість для критичної точки. З іншого боку,$x=6−6/\sqrt{55}$ знаходиться в домені. Оскільки ми звели в квадрат обидві сторони Equation\ ref {ex3eq2}, щоб досягти можливих критичних точок, залишається перевірити, що$x=6−6/\sqrt{55}$ відповідає рівнянню\ ref {ex3eq1}. Оскільки$x=6−6/\sqrt{55}$ задовольняє це рівняння, ми робимо висновок, що$x=6−6/\sqrt{55}$ це критична точка, і вона єдина. Щоб обґрунтувати, що час зведено до мінімуму для цього значення$x$, нам просто потрібно перевірити значення$T(x)$ в кінцевих точках$x=0$ і$x=6$, і порівняти їх зі значенням$T(x)$ в критичній точці$x=6−6/\sqrt{55}$. Ми знаходимо, що$T(0)≈2.108\,\text{h}$ і$T(6)≈1.417\,\text{h}$, тоді як

$$T(6−6/\sqrt{55})≈1.368\,\text{h}. \nonumber$$

Тому зробимо висновок, що$T$ має локальний мінімум в$x≈5.19$ mi.

Вправа$\PageIndex{3}$

Припустимо, острів$1$ знаходиться в милі від берега, а відстань від кабіни до точки на найближчому до острова березі -$15$ милі. Припустимо, відвідувач плаває зі швидкістю$2.5$ миль/год і біжить зі швидкістю$6$ миль/год. Нехай$x$ позначимо відстань, яку відвідувач пробіжить перед купанням, і знайде функцію за час, який потрібно відвідувачеві, щоб дістатися з каюти на острів.

Підказка

Час$T=T_{running}+T_{swimming}.$

Відповідь

$T(x)=\dfrac{x}{6}+\dfrac{\sqrt{(15−x)^2+1}}{2.5}$

У бізнесі компанії зацікавлені в максимізації доходу. У наступному прикладі ми розглянемо сценарій, в якому компанія зібрала дані про те, скільки автомобілів вона може взяти в оренду, залежно від ціни, яку вона стягує зі своїх клієнтів за оренду автомобіля. Давайте використаємо ці дані, щоб визначити ціну, яку компанія повинна стягувати, щоб максимізувати суму грошей, яку вона приносить.

Приклад$\PageIndex{4}$: Maximizing Revenue

Власники компанії з прокату автомобілів визначили, що якщо вони стягують з клієнтів$p$ доларів на добу за оренду автомобіля$50≤p≤200$, де кількість автомобілів, які$n$ вони орендують на день, можна моделювати лінійною функцією$n(p)=1000−5p$. Якщо вони стягують плату$$50$ за день або менше, вони візьмуть в оренду всі свої машини. Якщо вони стягують плату$$200$ за день або більше, вони не орендують жодних автомобілів. Припускаючи, що власники планують стягувати плату з клієнтів$$200$ за$$50$ день і на день, щоб орендувати автомобіль, скільки вони повинні стягувати, щоб максимізувати свій дохід?

Рішення

Крок 1: Нехай$p$ буде ціна, що стягується за машину на добу, і нехай$n$ буде кількість автомобілів, орендованих на день. Нехай$R$ буде дохід в день.

Крок 2: Проблема полягає в тому, щоб максимізувати$R.$

Крок 3: Дохід (за день) дорівнює кількості автомобілів, орендованих за день, що перевищує ціну, що стягується за машину на добу, тобто$R=n×p.$

Крок 4: Оскільки кількість автомобілів, орендованих на день, моделюється лінійною$n(p)=1000−5p,$ функцією, дохід$R$ може бути представлений функцією

$$\begin{align*} R(p) &=n×p \\[4pt] &=(1000−5p)p \\[4pt] &=−5p^2+1000p.\end{align*}$$

Крок 5: Оскільки власники планують стягувати плату між$$50$ автомобілем на добу та$$200$ за машину на добу, проблема полягає в тому, щоб знайти максимальний дохід$R(p)$$p$ за закритий проміжок часу$[50,200]$.

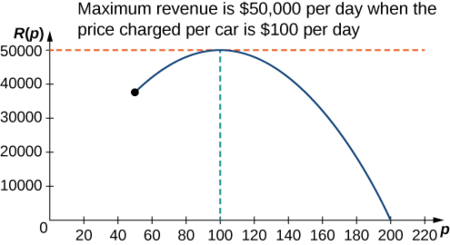
Крок 6: Оскільки$R$ є безперервною функцією над замкнутим обмеженим інтервалом$[50,200]$, вона має абсолютний максимум (і абсолютний мінімум) у цьому інтервалі. Щоб знайти максимальне значення, шукайте критичні точки. Похідна є$R′(p)=−10p+1000.$ Отже, критична точка є$p=100$. Коли$p=100, R(100)=$50,000.$ Коли$p=50, R(p)=$37,500$. Коли$p=200, R(p)=$0$.

Тому абсолютний максимум відбувається при$p=$100$. Компанія з прокату автомобілів повинна стягувати плату$$100$ за день за автомобіль, щоб максимізувати дохід, як показано на наступному малюнку.

Малюнок$\PageIndex{6}$: Щоб максимізувати дохід, компанія з прокату автомобілів повинна збалансувати ціну прокату проти кількості автомобілів, які люди будуть орендувати за цією ціною.

Вправа$\PageIndex{4}$

Компанія з прокату автомобілів стягує своїм клієнтам$p$ долари в день, де$60≤p≤150$. Він виявив, що кількість автомобілів, орендованих на день, може бути змодельована лінійною функцією$n(p)=750−5p.$ Скільки компанія повинна стягувати плату з кожного клієнта, щоб максимізувати дохід?

Підказка

$R(p)=n×p,$де$n$ вказана кількість орендованих машин і ціна, що$p$ нараховується за машину.

Відповідь

Компанія повинна стягувати плату$$75$ за автомобіль на добу.

Приклад$\PageIndex{5}$: Maximizing the Area of an Inscribed Rectangle

Прямокутник повинен бути вписаний в еліпс

$$\dfrac{x^2}{4}+y^2=1. \nonumber$$

Якими повинні бути розміри прямокутника, щоб максимально збільшити його площу? Яка максимальна площа?

Рішення

Крок 1: Щоб прямокутник був вписаний в еліпс, сторони прямокутника повинні бути паралельні осям. $L$Дозволяти довжина прямокутника і$W$ бути його шириною. $A$Дозволяти площа прямокутника.

Малюнок$\PageIndex{7}$: Ми хочемо максимально збільшити площу прямокутника, вписаного в еліпс.

Крок 2: Проблема полягає в тому, щоб максимізувати$A$.

Крок 3: Площа прямокутника дорівнює$A=LW.$

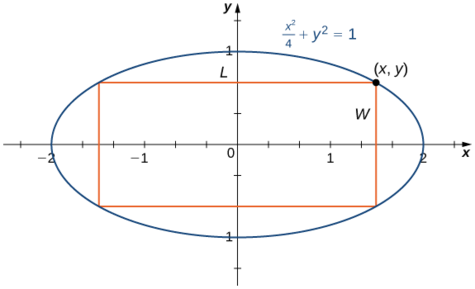
Крок 4:$(x,y)$ Дозволяти кут прямокутника, який лежить в першому квадранті, як показано на малюнку$\PageIndex{7}$. Ми можемо написати довжину$L=2x$ і ширину$W=2y$. З тих пір$\dfrac{x^2}{4}+y^2=1$ і$y>0$, у нас є$y=\sqrt{1-\dfrac{x^2}{4}}$. Тому площа - це

$A=LW=(2x)(2y)=4x\sqrt{1-\dfrac{x^2}{4}}=2x\sqrt{4−x^2}$

Крок 5: На малюнку ми бачимо$\PageIndex{7}$, що для вписання прямокутника в еліпс$x$ -координата кута в першому квадранті повинна задовольнити$0<x<2$. Тому проблема зводиться до пошуку максимального значення$A(x)$ над відкритим інтервалом$(0,2)$. Так як$A(x)$ буде мати абсолютний максимум (і абсолютний мінімум) над замкнутим інтервалом$[0,2]$, розглянемо$A(x)=2x\sqrt{4−x^2}$ над інтервалом$[0,2]$. Якщо абсолютний максимум виникає у внутрішній точці, то ми знайшли абсолютний максимум у відкритому інтервалі.

Крок 6: Як згадувалося раніше,$A(x)$ є безперервною функцією над замкнутим обмеженим інтервалом$[0,2]$. Тому вона має абсолютний максимум (і абсолютний мінімум). У кінцевих точках$x=0$ і$x=2$,$A(x)=0.$ для$0<x<2$,$A(x)>0$.

Тому максимум повинен відбуватися в критичній точці. Взявши похідну від$A(x)$, отримуємо

$$\begin{align*} A'(x) &=2\sqrt{4−x^2}+2x⋅\dfrac{1}{2\sqrt{4−x^2}}(−2x) \\[4pt] &=2\sqrt{4−x^2}−\dfrac{2x^2}{\sqrt{4−x^2}} \\[4pt] &=\dfrac{8−4x^2}{\sqrt{4−x^2}} . \end{align*}$$

Щоб знайти критичні точки, нам потрібно знайти де$A'(x)=0.$ Ми можемо бачити, що$x$ це рішення

$$\dfrac{8−4x^2}{\sqrt{4−x^2}}=0, \label{ex5eq1}$$

то$x$ повинні задовольнити

$$8−4x^2=0. \nonumber$$

Отже,$x^2=2.$ таким чином,$x=±\sqrt{2}$ можливі розв'язки рівняння\ ref {ex5eq1}. Оскільки ми розглядаємо$x$ протягом інтервалу$[0,2]$,$x=\sqrt{2}$ є можливість для критичної точки, але не$x=−\sqrt{2}$ є. Тому ми перевіряємо, чи$\sqrt{2}$ є розв'язком Рівняння\ ref {ex5eq1}. Оскільки$x=\sqrt{2}$ є розв'язком Equation\ ref {ex5eq1}, то робимо висновок, що$\sqrt{2}$ це єдина критична точка$A(x)$ в інтервалі$[0,2]$.

Тому$A(x)$ повинен мати абсолютний максимум в критичній точці$x=\sqrt{2}$. Щоб визначити розміри прямокутника, нам потрібно знайти довжину$L$ і ширину$W$. Якщо$x=\sqrt{2}$ тоді

$$y=\sqrt{1−\dfrac{(\sqrt{2})^2}{4}}=\sqrt{1−\dfrac{1}{2}}=\dfrac{1}{\sqrt{2}}.\nonumber$$

Тому розміри прямокутника складають$L=2x=2\sqrt{2}$ і$W=2y=\dfrac{2}{\sqrt{2}}=\sqrt{2}$. Площа цього прямокутника дорівнює$A=LW=(2\sqrt{2})(\sqrt{2})=4.$

Вправа$\PageIndex{5}$

Змініть функцію площі,$A$ якщо прямокутник має бути вписаний в одиничне коло$x^2+y^2=1$. Що таке область розгляду?

Підказка

Якщо$(x,y)$ вершина квадрата, яка лежить в першому квадранті, то площа квадрата дорівнює$A=(2x)(2y)=4xy.$

Відповідь

$A(x)=4x\sqrt{1−x^2}.$Домен розгляду є$[0,1]$.

Розв'язування задач оптимізації, коли інтервал не закритий або необмежений

У попередніх прикладах ми розглядали функції на замкнутих обмежених доменах. Отже, за теоремою екстремальних значень ми гарантували, що функції мають абсолютну крайність. Розглянемо тепер функції, для яких домен не є ні замкнутим, ні обмеженим.

Багато функцій все ще мають принаймні одну абсолютну крайність, навіть якщо домен не закритий або домен необмежений. Наприклад, функція$f(x)=x^2+4$ over$(−∞,∞)$ має абсолютний мінімум$4$ at$x=0$. Тому ми все ще можемо розглянути функції над необмеженими доменами або відкритими інтервалами і визначити, чи мають вони абсолютну крайність. У наступному прикладі ми спробуємо мінімізувати функцію над необмеженим доменом. Ми побачимо, що, хоча область$(0,∞),$ розгляду - функція має абсолютний мінімум.

У наступному прикладі ми розглянемо конструювання коробки найменшої площі поверхні із заданим обсягом. Неважко показати, що для коробки з закритим верхом, по симетрії, серед всіх коробок із заданим обсягом куб матиме найменшу площу поверхні. Отже, розглянуто модифіковану задачу визначення того, яка коробка з відкритим верхом із заданим об'ємом має найменшу площу поверхні.

Приклад$\PageIndex{6}$: Minimizing Surface Area

Буде побудована прямокутна коробка з квадратною основою, відкритим верхом і об'ємом.$216 \,\text{in}^3$ Якими повинні бути розміри короба, щоб мінімізувати площу поверхні коробки? Яка мінімальна площа поверхні?

Рішення

Крок 1: Намалюйте прямокутну коробку та введіть змінну,$x$ щоб представити довжину кожної сторони квадратної основи; нехай$y$ представляють висоту коробки. Нехай$S$ позначимо площу поверхні коробки з відкритим верхом.

Малюнок$\PageIndex{8}$: Ми хочемо мінімізувати площу поверхні квадратної коробки із заданим обсягом.

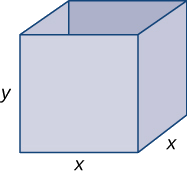
Крок 2: Нам потрібно мінімізувати площу поверхні. Тому потрібно звести до мінімуму$S$.

Крок 3: Оскільки коробка має відкритий верх, нам потрібно лише визначити площу чотирьох вертикальних сторін і підстави. Площа кожної з чотирьох вертикальних сторін - це$x⋅y.$ Площа підстави$x^2$. Тому площа поверхні короба дорівнює

$S=4xy+x^2$.

Крок 4: Оскільки обсяг цього поля є,$x^2y$ а обсяг задається як$216\,\text{in}^3$, рівняння обмеження є

$x^2y=216$.

Розв'язуючи рівняння обмеження для$y$, ми маємо$y=\dfrac{216}{x^2}$. Тому ми можемо записати площу поверхні як функцію$x$ лише:

$$S(x)=4x\left(\dfrac{216}{x^2}\right)+x^2.\nonumber$$

Тому,$S(x)=\dfrac{864}{x}+x^2$.

Крок 5: Оскільки ми цього вимагаємо$x^2y=216$, ми не можемо мати$x=0$. Тому нам і потрібно$x>0$. З іншого боку,$x$ допускається мати будь-яке позитивне значення. Зверніть увагу, що коли$x$ стає великим, висота коробки$y$ стає відповідно маленькою, так що$x^2y=216$. Точно так само, як$x$ стає маленьким, висота коробки стає відповідно великою. Зробимо висновок, що домен є відкритим необмеженим інтервалом$(0,∞)$. Зауважте, що, на відміну від попередніх прикладів, ми не можемо звести нашу проблему до пошуку абсолютного максимуму або абсолютного мінімуму через замкнутий обмежений інтервал. Однак на наступному кроці ми з'ясуємо, чому ця функція повинна мати абсолютний мінімум протягом інтервалу$(0,∞).$

Крок 6: Зверніть увагу, що як$x→0^+,\, S(x)→∞.$ також, як$x→∞, \,S(x)→∞$. Оскільки$S$ це безперервна функція, яка наближається до нескінченності на кінцях, вона повинна мати абсолютний мінімум у деяких$x∈(0,∞)$. Цей мінімум повинен відбуватися в критичній точці$S$. Похідна - це

$$S′(x)=−\dfrac{864}{x^2}+2x.\nonumber$$

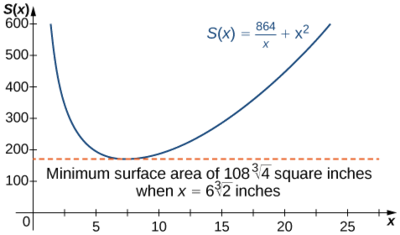
Тому$S′(x)=0$ коли$2x=\dfrac{864}{x^2}$. Вирішуючи це рівняння для$x$$x^3=432$, отримаємо,$x=\sqrt[3]{432}=6\sqrt[3]{2}.$ так як це єдина критична точка$S$, абсолютний мінімум повинен відбуватися при$x=6\sqrt[3]{2}$ (див. Рис.$\PageIndex{9}$).

Коли$x=6\sqrt[3]{2}$,$y=\dfrac{216}{(6\sqrt[3]{2})^2}=3\sqrt[3]{2}\,\text{in.}$ отже, розміри коробки повинні бути$x=6\sqrt[3]{2}\,\text{in.}$ і$y=3\sqrt[3]{2}\,\text{in.}$ при цих розмірах площа поверхні дорівнює

$$S(6\sqrt[3]{2})=\dfrac{864}{6\sqrt[3]{2}}+(6\sqrt[3]{2})^2=108\sqrt[3]{4}\,\text{in}^2\nonumber$$

Малюнок$\PageIndex{9}$: Ми можемо використовувати графік для визначення розмірів коробки заданого обсягу і мінімальної площі поверхні.

Вправа$\PageIndex{6}$

Розглянемо ту ж коробку з відкритим верхом, яка повинна мати обсяг$216\,\text{in}^3$. Припустимо, вартість матеріалу для основи є$20¢/\text{in}^2$ і вартість матеріалу для бортів є$30¢/\text{in}^2$ і ми намагаємося мінімізувати витрати на цей короб. Запишіть вартість як функцію довжини сторін підстави. ($x$Дозволяти бути довжина сторони підстави і$y$ бути висотою коробки.)

Підказка

Якщо вартість однієї зі сторін, то$30¢/\text{in}^2,$ вартість цієї сторони дорівнює$0.30xy$ доларам.

Відповідь

$c(x)=\dfrac{259.2}{x}+0.2x^2$доларів

Ключові поняття

• Щоб вирішити задачу оптимізації, почніть з малюнка і введення змінних.
• Знайдіть рівняння, що стосується змінних.
• Знайдіть функцію однієї змінної, щоб описати величину, яку потрібно звести до мінімуму або максимізувати.
• Шукайте критичні точки, щоб знайти локальні екстреми.

Глосарій

проблеми оптимізації

задачі, які вирішуються шляхом знаходження максимального або мінімального значення функції