4.5: Похідні та форма графіка
- Page ID
- 62136
- Поясніть, як знак першої похідної впливає на форму графіка функції.
- Створіть перший тест похідної для критичних точок.
- Використовуйте точки увігнутості та перегину, щоб пояснити, як знак другої похідної впливає на форму графіка функції.
- Поясніть тест на увігнутість для функції через відкритий інтервал.
- Поясніть зв'язок між функцією та її першою та другою похідними.
- Створіть другий похідний тест на локальну екстрему.
Раніше в цьому розділі ми заявляли, що якщо функція\(f\) має локальний екстремум в точці\(c\), то\(c\) повинна бути критичною точкою\(f\). Однак функція не гарантується мати локальний екстремум в критичній точці. Наприклад,\(f(x)=x^3\) має критичну точку в\(x=0\) так як\(f'(x)=3x^2\) дорівнює нулю в\(x=0\), але\(f\) не має локального екстремуму при\(x=0\). Використовуючи результати попереднього розділу, ми тепер можемо визначити, чи відповідає критична точка функції локальному екстремальному значенню. У цьому розділі ми також бачимо, як друга похідна надає інформацію про форму графіка, описуючи, чи кривий графік функції вгору або криві вниз.
Перший похідний тест
\(3\)Наслідок теореми про середнє значення показав, що якщо похідна функції є додатною протягом інтервалу,\(I\) то функція збільшується\(I\). З іншого боку, якщо похідна функції є негативною протягом інтервалу\(I\), то функція зменшується,\(I\) як показано на наступному малюнку.
Безперервна функція\(f\) має локальний максимум в точці\(c\) тоді і тільки тоді, коли\(f\) переходить від збільшення до зменшення в точці\(c\). Аналогічно,\(f\) має локальний мінімум при\(c\) якщо і тільки в тому випадку, якщо\(f\) переходить від зменшення до збільшення на\(c\). Якщо\(f\) є безперервною функцією протягом інтервалу,\(I\) що містить\(c\) і диференціюється над\(I\), за винятком\(c\), можливо, в, єдиним способом\(f\) можна перейти від збільшення до зменшення (або навпаки) в точці\(c\) є якщо\(f'\) зміни ознака як \(x\)збільшується через\(c\). Якщо\(f\) диференціюється в\(c\), єдиний спосіб, який\(f'\) може змінити знак, як\(x\) збільшується через\(c\) це якщо\(f'(c)=0\). Отже, для функції,\(f\) яка є безперервною протягом інтервалу,\(I\) що містить\(c\) і диференціюється над\(I\), за винятком\(c\), можливо, at, єдиним способом\(f\) може перейти від збільшення до зменшення (або навпаки) є якщо\(f'(c)=0\) або\(f'(c)\) не визначено. Отже, щоб знайти локальні екстремуми для функції\(f\), ми шукаємо точки\(c\) в області\(f\) таких,\(f'(c)\) що\(f'(c)=0\) або не визначено. Нагадаємо, що такі точки називаються критичними точками\(f\).
Зверніть увагу, що не\(f\) потрібно мати локальну крайність в критичній точці. Критичними моментами є кандидати лише на локальну екстрему. На малюнку ми показуємо\(\PageIndex{2}\), що якщо неперервна функція\(f\) має локальний екстремум, вона повинна відбуватися в критичній точці, але функція може не мати локального екстремуму в критичній точці. Показано, що якщо\(f\) має локальний екстремум у критичній точці, то знак\(f'\) перемикачів як\(x\) збільшується через цю точку.
Використовуючи рис.\(\PageIndex{2}\), підсумовуємо основні результати щодо локальних екстремумів.
- Якщо безперервна функція\(f\) має локальний екстремум, вона повинна відбуватися в критичній точці\(c\).
- Функція має локальний екстремум у критичній точці\(c\) тоді і лише тоді, коли похідні\(f'\) перемикачі\(x\) знаходять як збільшення\(c\).
- Тому, щоб перевірити, чи має функція локальний екстремум в критичній точці\(c\), ми повинні визначити знак зліва і справа від\(c\).\(f'(x)\)
Цей результат відомий як перший похідний тест.
Припустимо, що\(f\) це безперервна функція протягом інтервалу,\(I\) що містить критичну точку\(c\). Якщо\(f\) диференціюється над\(I\), крім можливо в точці\(c\), то\(f(c)\) задовольняє одному з наступних описів:
- Якщо\(f'\) змінюється знак від позитивного коли\(x<c\) до негативного коли\(x>c\), то\(f(c)\) є локальним максимумом\(f\).
- Якщо\(f'\) змінюється знак від негативного коли\(x<c\) до позитивного коли\(x>c\),\(f(c)\) то локальний мінімум\(f\).
- Якщо\(f'\) має однаковий знак для\(x<c\) і\(x>c\), то не\(f(c)\) є ні локальним максимумом, ні локальним мінімумом\(f\)
Тепер давайте розглянемо, як використовувати цю стратегію, щоб знайти всі локальні екстремуми для певних функцій.
Використовуйте перший похідний тест, щоб знайти розташування всіх локальних\(f(x)=x^3−3x^2−9x−1.\) екстремумів для Використовуйте графічну утиліту для підтвердження результатів.
Рішення
Крок 1. Похідна -\(f'(x)=3x^2−6x−9.\) Щоб знайти критичні точки, нам потрібно знайти, де\(f'(x)=0.\) Факторинг полінома, робимо висновок, що критичні точки повинні задовольняти
\[3(x^2−2x−3)=3(x−3)(x+1)=0. \nonumber \]
Тому критичні точки\(x=3,−1.\) тепер ділять інтервал\((−∞,∞)\) на менші інтервали\((−∞,−1),(−1,3)\) і\((3,∞).\)
Крок 2. Оскільки\(f'\) є безперервною функцією, для визначення знака\(f'(x)\) над кожним субінтервалом досить вибрати точку над кожним з інтервалів\((−∞,−1),(−1,3)\)\((3,∞)\) і визначити знак\(f'\) в кожній з цих точок. Наприклад, давайте виберемо\(x=−2\)\(x=0\), і в\(x=4\) якості контрольних точок.
| Інтервал | Тестова точка | Знак\(f'(x)=3(x−3)(x+1)\) на випробувальному пункті | Висновок |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f' (x) =3 (x−3) (x+1)\) у тестовій точці» style="вертикальне вирівнювання: середина; "> (+) (−) (−) =+ | \(f\)збільшується. |
| \((−1,3)\) | \(x=0\) | \ (f' (x) =3 (x−3) (x+1)\) у тестовій точці» style="вертикальне вирівнювання: середина; "> (+) (+) (+) =- | \(f\)зменшується. |
| \((3,∞)\) | \(x=4\) | \ (f' (x) =3 (x−3) (x+1)\) у тестовій точці» style="вертикальне вирівнювання: середина; "> (+) (+) (+) =+ | \(f\)збільшується. |
Крок 3. Так як\(f'\) перемикає знак з позитивного на негативний у міру\(x\) збільшення\(f\) наскрізного\(-1\), має локальний максимум при\(x=−1\). Так як\(f'\) перемикає знак з негативного на позитивний, оскільки\(x\) збільшується наскрізь\(3\),\(f\) має локальний мінімум при\(x=3\). Ці аналітичні результати узгоджуються з наступним графіком.
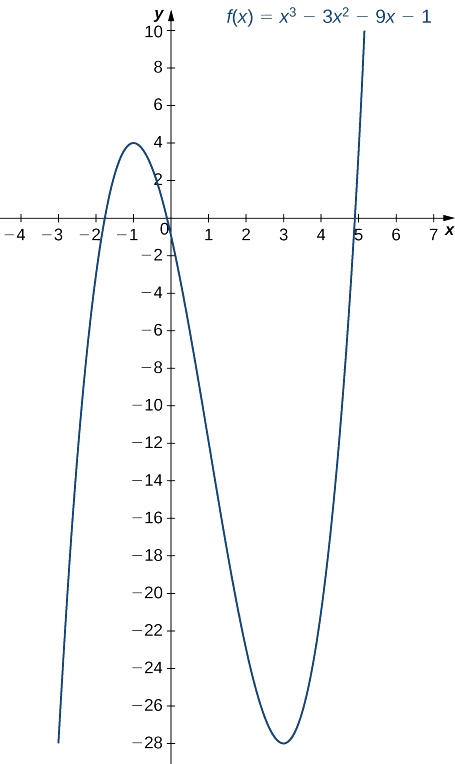
Використовуйте перший похідний тест, щоб знайти всі локальні екстреми для\(f(x)=−x^3+\frac{3}{2}x^2+18x.\)
- Підказка
-
Знайдіть всі критичні точки\(f\) і визначте ознаки\(f'(x)\) над конкретними інтервалами, визначеними критичними точками.
- Відповідь
-
\(f\)має локальний мінімум на\(−2\) і локальний максимум при\(3\).
Використовуйте перший похідний тест, щоб знайти розташування всіх локальних\(f(x)=5x^{1/3}−x^{5/3}.\) екстремумів для Використовуйте графічну утиліту для підтвердження результатів.
Рішення
Крок 1. Похідна - це
\[f'(x)=\frac{5}{3}x^{−2/3}−\frac{5}{3}x^{2/3}=\frac{5}{3x^{2/3}}−\frac{5x^{2/3}}{3}=\frac{5−5x^{4/3}}{3x^{2/3}}=\frac{5(1−x^{4/3})}{3x^{2/3}}.\nonumber \]
Похідна,\(f'(x)=0\) коли\(1−x^{4/3}=0.\) Тому,\(f'(x)=0\) в\(x=±1\). Похідна\(f'(x)\) не визначена в\(x=0.\) Тому ми маємо три критичні точки:\(x=0\),\(x=1\), і\(x=−1\). Отже, розділіть інтервал\((−∞,∞)\) на менші інтервали\((−∞,−1),\,(−1,0),\,(0,1)\), і\((1,∞)\).
Крок 2: Оскільки\(f'\) є безперервним протягом кожного субінтервалу, досить вибрати контрольну точку\(x\) в кожному з інтервалів з кроку 1 і визначити знак\(f'\) в кожній з цих точок. Точки\(x=−2,\,x=−\frac{1}{2},\,x=\frac{1}{2}\), і\(x=2\) є контрольними точками для цих інтервалів.
| Інтервал | Тестова точка | Знак\(f'(x)=\frac{5(1−x^{4/3})}{3x^{2/3}}\) на випробувальному пункті | Висновок |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f' (x) =\ frac {5 (1−x^ {4/3})} {3x^ {2/3}}\) у випробувальній точці» style="вертикальне вирівнювання: середина; ">\(\frac{(+)(−)}{+}=−\) | \(f\)зменшується. |
| \((−1,0)\) | \(x=−\frac{1}{2}\) | \ (f' (x) =\ frac {5 (1−x^ {4/3})} {3x^ {2/3}}\) у випробувальній точці» style="вертикальне вирівнювання: середина; ">\(\frac{(+)(+)}{+}=+\) | \(f\)збільшується. |
| \((0,1)\) | \(x=\frac{1}{2}\) | \ (f' (x) =\ frac {5 (1−x^ {4/3})} {3x^ {2/3}}\) у випробувальній точці» style="вертикальне вирівнювання: середина; ">\(\frac{(+)(+)}{+}=+\) | \(f\)збільшується. |
| \((1,∞)\) | \(x=2\) | \ (f' (x) =\ frac {5 (1−x^ {4/3})} {3x^ {2/3}}\) у випробувальній точці» style="вертикальне вирівнювання: середина; ">\(\frac{(+)(−)}{+}=−\) | \(f\)зменшується. |
Крок 3: Оскільки\(f\) зменшується за інтервал\((−∞,−1)\) і збільшується за інтервал\((−1,0)\),\(f\) має локальний мінімум при\(x=−1\). Так як\(f\) збільшується над інтервалом\((−1,0)\) і інтервалом\((0,1)\),\(f\) не має локального екстремуму при\(x=0\). Так як\(f\) збільшується за інтервал\((0,1)\) і зменшується за інтервал\((1,∞)\),\(f\) має локальний максимум при\(x=1\). Аналітичні результати узгоджуються з наступним графіком.
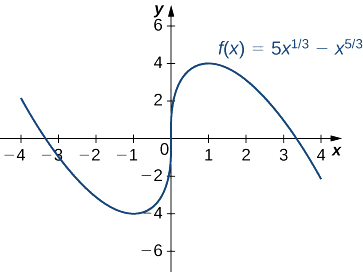
Використовуйте перший похідний тест, щоб знайти всі локальні екстремуми для\(f(x)=\dfrac{3}{x−1}\).
- Підказка
-
Єдина критична точка\(f\) - це\(x=1.\)
- Відповідь
-
\(f\)не має локальної крайності, тому що\(f'\) не змінює знак на\(x=1\).
Увігнутість і точки перегину
Тепер ми знаємо, як визначити, де функція збільшується або зменшується. Однак є ще одне питання, яке слід розглянути щодо форми графіка функції. Якщо графік кривий, це крива вгору або крива вниз? Це поняття називається увігнутістю функції.
\(\PageIndex{5a}\)На малюнку показана функція\(f\) з графіком, який кривий вгору. Зі\(x\) збільшенням нахил дотичної лінії збільшується. Таким чином, оскільки похідна збільшується зі\(x\) збільшенням,\(f'\) є зростаючою функцією. Ми говоримо, що\(f\) ця функція увігнута вгору. \(\PageIndex{5b}\)На малюнку показана функція\(f\), яка крива вниз. Зі\(x\) збільшенням нахил дотичної лінії зменшується. Оскільки похідна зменшується зі\(x\) збільшенням,\(f'\) є спадною функцією. Ми говоримо, що\(f\) ця функція увігнута вниз.
\(f\)Дозволяти функція, яка диференціюється через відкритий інтервал\(I\). Якщо\(f'\) збільшується більше\(I\), ми говоримо\(f\), увігнуті вгору\(I\). Якщо\(f'\) зменшується\(I\), ми говоримо\(f\), увігнута вниз\(I\).
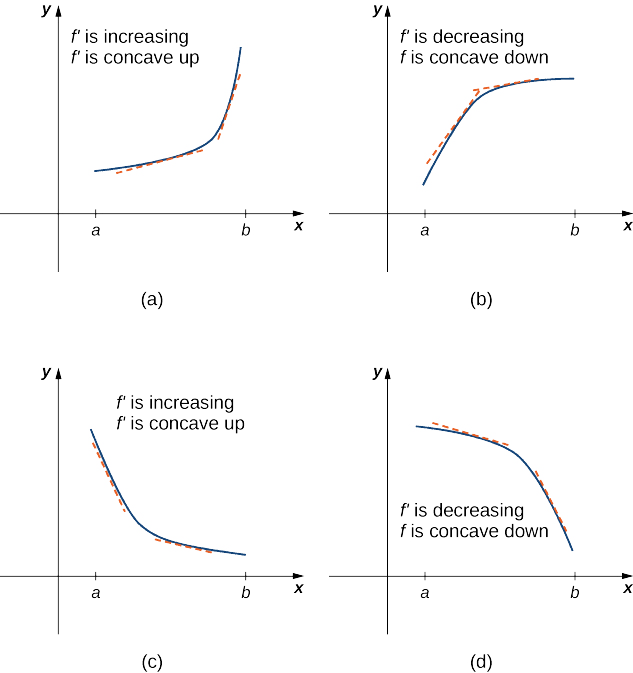
Загалом, не маючи графіка функції\(f\), як ми можемо визначити її увігнутість? За визначенням функція\(f\) увігнута вгору, якщо\(f'\) збільшується. З Слідство ми знаємо\(3\), що якщо\(f'\) є диференційованою функцією, то\(f'\) збільшується, якщо її похідна\(f''(x)>0\). Тому функція,\(f\) яка двічі диференційована, увігнута, коли\(f''(x)>0\). \(f\)Аналогічно функція увігнута вниз, якщо\(f'\) зменшується. Ми знаємо, що диференційовна функція\(f'\) зменшується, якщо її похідна\(f''(x)<0\). Тому двічі\(f\) диференційована функція увігнута вниз, коли\(f''(x)<0\). Застосування цієї логіки відоме як тест на увігнутість.
\(f\)Дозволяти функція, яка двічі диференціюється протягом інтервалу\(I\).
- Якщо\(f''(x)>0\) для всіх\(x∈I\),\(f\) то увігнута вгору\(I\)
- Якщо\(f''(x)<0\) для всіх\(f\),\(x∈I,\) то увігнута вниз\(I\).
Зроблено висновок, що можна визначити увігнутість функції, дивлячись\(f\) на другу похідну від\(f\). Крім того, ми спостерігаємо, що функція\(f\) може перемикати увігнутість (рис.\(\PageIndex{6}\)). Однак безперервна функція може перемикати увігнутість лише в точці,\(x\) якщо\(f''(x)=0\) або\(f''(x)\) не визначено. Отже, для визначення інтервалів, де функція\(f\) увігнута вгору і увігнута вниз, шукаємо ті значення\(x\) де\(f''(x)=0\) або\(f''(x)\) не визначено. Коли ми визначили ці точки, ми ділимо область\(f\) на менші інтервали і визначаємо знак\(f''\) над кожним з цих менших інтервалів. Якщо\(f''\) зміни знаком, як ми проходимо через точку\(x\), то\(f\) змінюється увігнутість. Важливо пам'ятати, що функція не\(f\) може змінювати увігнутість у точці,\(x\) навіть якщо\(f''(x)=0\) вона не\(f''(x)\) визначена. Якщо,\(f\) однак, змінити увігнутість в точці\(a\) і\(f\) безперервно в\(a\), ми говоримо, що точка\((a,f(a))\) є точкою перегину\(f\).
Якщо\(f\) є безперервним в\(a\) і\(f\) змінюється увігнутість в\(a\), точка\((a, \,f(a))\) є точкою перегину\(f\).
Для функції\(f(x)=x^3−6x^2+9x+30,\) визначають всі інтервали, де\(f\) увігнуті вгору і всі проміжки,\(f\) де увігнуті вниз. Перерахуйте всі точки перегину для\(f\). Використовуйте утиліту графіків, щоб підтвердити свої результати.
Рішення
Щоб визначити увігнутість, нам потрібно знайти другу похідну.\(f''(x).\) Перша похідна\(f'(x)=3x^2−12x+9,\) така друга похідна -\(f''(x)=6x−12.\) Якщо функція змінює увігнутість, вона виникає або коли,\(f''(x)=0\) або не\(f''(x)\) визначена. Так як\(f''\) визначається для всіх дійсних чисел\(x\), нам потрібно тільки знайти де\(f''(x)=0\). Вирішуючи рівняння\(6x−12=0\), ми бачимо, що\(x=2\) це єдине місце, де\(f\) могла змінитися увігнутість. Тепер тестуємо точки по проміжках\((−∞,2)\) і\((2,∞)\) для визначення увігнутості\(f\). Окуляри\(x=0\) і\(x=3\) є контрольними точками для цих інтервалів.
| Інтервал | Тестова точка | Знак\(f''(x)=6x−12\) на випробувальному пункті | Висновок |
|---|---|---|---|
| \((−∞,2)\) | \(x=0\) | \ (f "(x) =6x−12\) у тестовій точці» style="вертикальне вирівнювання: middle; ">− | \(f\)увігнутий вниз |
| \((2,∞)\) | \(x=3\) | \ (f "(x) =6x−12\) у тестовій точці» style="вертикальне вирівнювання: середина; ">+ | \(f\)увігнута вгору |
Робимо висновок,\(f\) що увігнутий вниз по проміжку\((−∞,2)\) і увігнутий вгору над інтервалом\((2,∞)\). Оскільки\(f\) змінюється увігнутість в\(x=2\), точка\((2,f(2))=(2,32)\) є точкою перегину. Малюнок\(\PageIndex{7}\) підтверджує аналітичні результати.
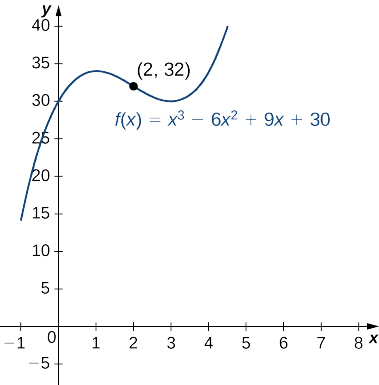
Для\(f(x)=−x^3+\frac{3}{2}x^2+18x\), знайти всі проміжки, де\(f\) увігнуті вгору і всі проміжки,\(f\) де увігнуті вниз.
- Підказка
-
Знайти де\(f''(x)=0\)
- Відповідь
-
\(f\)увігнута вгору за інтервал\((−∞,\frac{1}{2})\) і увігнута вниз протягом інтервалу\((\frac{1}{2},∞)\)
Тепер ми підсумовуємо в таблиці інформацію\(\PageIndex{4}\), яку перша та друга похідні функції\(f\) надають про графік\(f\), і ілюструємо цю інформацію на рис\(\PageIndex{8}\).
| Знак\(f'\) | Знак\(f''\) | \(f\)Збільшується чи зменшується? | Увігнутість |
|---|---|---|---|
| \ (f'\)» style="Вертикальне вирівнювання: середина; "> Позитивне | \ (f "\)» style="Вертикальне вирівнювання: середина; "> Позитивне | \ (f\) збільшення або зменшення?» style="вертикальне вирівнювання: середина; "> Збільшення | увігнуті вгору |
| \ (f'\)» style="Вертикальне вирівнювання: середина; "> Позитивне | \ (f "\)» style="Вертикальне вирівнювання: середина; "> Негативний | \ (f\) збільшення або зменшення?» style="вертикальне вирівнювання: середина; "> Збільшення | увігнуті вниз |
| \ (f'\)» style="Вертикальне вирівнювання: середина; "> Негативний | \ (f "\)» style="Вертикальне вирівнювання: середина; "> Позитивне | \ (f\) збільшення або зменшення?» style="вертикальне вирівнювання: по середині; "> Зменшення | увігнуті вгору |
| \ (f'\)» style="Вертикальне вирівнювання: середина; "> Негативний | \ (f "\)» style="Вертикальне вирівнювання: середина; "> Негативний | \ (f\) збільшення або зменшення?» style="вертикальне вирівнювання: по середині; "> Зменшення | увігнуті вниз |
Другий похідний тест
Перший похідний тест забезпечує аналітичний інструмент для знаходження локальних екстремумів, але друга похідна також може бути використана для визначення екстремальних значень. Використання другої похідної іноді може бути більш простим методом, ніж використання першої похідної.
Ми знаємо, що якщо безперервна функція має локальний екстремум, вона повинна відбуватися в критичній точці. Однак функція не повинна мати локальний екстремум в критичній точці. Тут ми розглянемо, як другий тест похідної може бути використаний для визначення того, чи має функція локальний екстремум у критичній точці. Дозволяти\(f\) бути двічі диференційовний функція така, що\(f'(a)=0\) і\(f''\) є безперервним протягом відкритого інтервалу,\(I\) що містить\(a\). Припустимо\(f''(a)<0\). Так як\(f''\) є безперервним\(I, f''(x)<0\) для всіх\(x∈I\) (рис.\(\PageIndex{9}\)). Тоді, за наслідками\(3\),\(f'\) є спадною функцією над\(I\). Так як\(f'(a)=0\), робимо висновок, що для всіх\(x∈I, \,f'(x)>0\) якщо\(x<a\) і\(f'(x)<0\) якщо\(x>a\). Тому, за першим похідним тестом,\(f\) має локальний максимум при\(x=a\).
З іншого боку, припустимо, існує\(b\) такий момент, що\(f'(b)=0\) але\(f''(b)>0\). Так як\(f''\) є безперервним над відкритим інтервалом\(I\) містить\(b\), то\(f''(x)>0\) для всіх\(x∈I\) (рис.\(\PageIndex{9}\)). Тоді, за наслідками\(3\),\(f'\) є зростаючою функцією над\(I\). Так як\(f'(b)=0\), робимо висновок, що для всіх\(x∈I\),\(f'(x)<0\) якщо\(x<b\) і\(f'(x)>0\) якщо\(x>b\). Тому, за першим похідним тестом,\(f\) має локальний мінімум при\(x=b.\)
Припустимо\(f''\),\(f'(c)=0\) і є безперервним протягом інтервалу, що містить\(c\).
- Якщо\(f''(c)>0\), то\(f\) має локальний мінімум при\(c\).
- Якщо\(f''(c)<0\), то\(f\) має локальний максимум при\(c\).
- Якщо\(f''(c)=0,\) тоді тест непереконливий.
Зверніть увагу, що для випадку III. коли\(f''(c)=0\), то\(f\) може мати локальний максимум, локальний мінімум, або ні на\(c\). Наприклад, функції\(f(x)=x^3, \; f(x)=x^4,\) і\(f(x)=−x^4\) всі мають критичні точки на\(x=0\). У кожному випадку друга похідна дорівнює нулю при\(x=0\). Однак функція\(f(x)=x^4\) має локальний мінімум,\(x=0\) тоді як функція\(f(x)=−x^4\) має локальний максимум at\(x=0\), а функція\(f(x)=x^3\) не має локального екстремуму at\(x=0\).
Давайте тепер розглянемо, як використовувати другий тест похідної, щоб визначити, чи\(f\) має локальний максимум або локальний мінімум в критичній точці\(c\), де\(f'(c)=0.\)
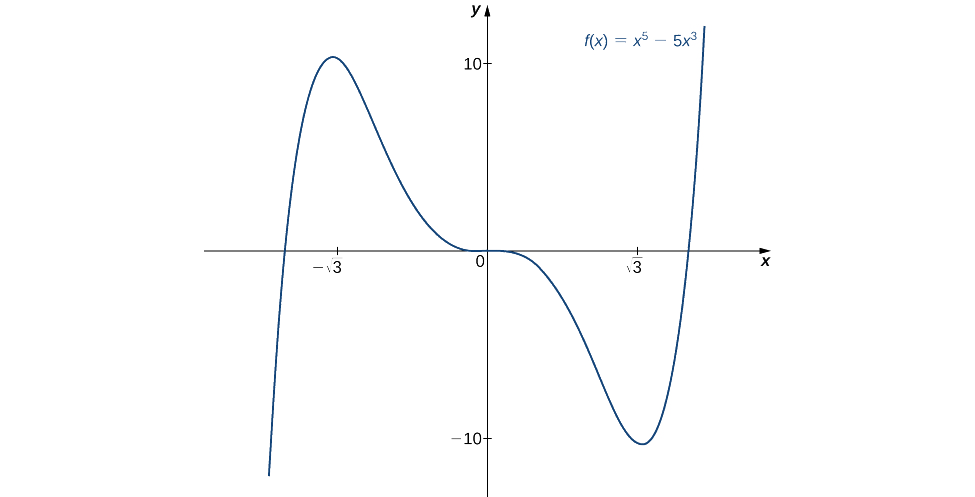
Використовуйте другу похідну, щоб знайти розташування всіх локальних екстрем для\(f(x)=x^5−5x^3.\)
Рішення
Щоб застосувати другий похідний тест, нам спочатку потрібно знайти критичні точки\(c\) де\(f'(c)=0\). Похідна є\(f'(x)=5x^4−15x^2\). Тому\(f'(x)=5x^4−15x^2=5x^2(x^2−3)=0\) коли\(x=0,\,±\sqrt{3}\).
Щоб визначити, чи\(f\) має локальний екстремум в будь-якій з цих точок, нам потрібно оцінити ознаку\(f''\) в цих точках. Друга похідна -
\(f''(x)=20x^3−30x=10x(2x^2−3).\)
У наступній таблиці ми оцінюємо другу похідну в кожній з критичних точок і використовуємо другий тест похідної, щоб визначити, чи\(f\) має локальний максимум або локальний мінімум в будь-якій з цих точок.
| \(x\) | \(f''(x)\) | Висновок |
|---|---|---|
| \ (x\) ">\(−\sqrt{3}\) | \ (f "(x)\)" >\(−30\sqrt{3}\) | Локальний максимум |
| \ (x\) ">\(0\) | \ (f "(x)\)" >\(0\) | Другий похідний тест є непереконливим |
| \ (x\) ">\(\sqrt{3}\) | \ (f "(x)\)" >\(30\sqrt{3}\) | Локальний мінімум |
За другим похідним тестом ми робимо висновок, що\(f\) має локальний максимум при\(x=−\sqrt{3}\) і\(f\) має локальний мінімум при\(x=\sqrt{3}\). Другий похідний тест є безрезультатним при\(x=0\). Щоб визначити, чи\(f\) має локальна крайність у,\(x=0,\) ми застосуємо перший похідний тест. Оцінити знак\(f'(x)=5x^2(x^2−3)\) для\(x∈(−\sqrt{3},0)\) і\(x∈(0,\sqrt{3})\), нехай\(x=−1\) і\(x=1\) бути двома тестовими точками. Оскільки\(f'(−1)<0\) і\(f'(1)<0\), ми робимо висновок, що\(f\) зменшується на обох інтервалах і, отже,\(f\) не має локальної крайності на,\(x=0\) як показано на наступному графіку.
Розглянемо функцію\(f(x)=x^3−(\frac{3}{2})x^2−18x\). Окуляри\(c=3,\,−2\) задовольняють\(f'(c)=0\). Використовуйте другий тест похідної, щоб визначити, чи\(f\) має локальний максимум або локальний мінімум в цих точках.
- Підказка
-
\(f''(x)=6x−3\)
- Відповідь
-
\(f\)має локальний максимум at\(−2\) і локальний мінімум на\(3\).
Зараз ми розробили інструменти, необхідні для визначення того, де функція збільшується і зменшується, а також отримали розуміння основної форми графіка. У наступному розділі ми обговорюємо, що відбувається з функцією як\(x→±∞.\) На цьому етапі у нас є достатньо інструментів, щоб забезпечити точні графіки великої кількості функцій.
Ключові поняття
- Якщо\(c\) є критичною точкою\(f\) і\(f'(x)>0\) за\(x<c\) і\(f'(x)<0\) для\(x>c\), то\(f\) має локальний максимум при\(c\).
- Якщо\(c\) є критичною точкою\(f\) і\(f'(x)<0\) для\(x<c\) і\(f'(x)>0\) для,\(x>c,\) то\(f\) має локальний мінімум при\(c\).
- Якщо\(f''(x)>0\) над інтервалом\(I\),\(f\) то увігнута вгору\(I\).
- Якщо\(f''(x)<0\) над інтервалом\(I\),\(f\) то увігнута вниз\(I\).
- Якщо\(f'(c)=0\) і\(f''(c)>0\), то\(f\) має локальний мінімум при\(c\).
- Якщо\(f'(c)=0\) і\(f''(c)<0\), то\(f\) має локальний максимум при\(c\).
- Якщо\(f'(c)=0\) і\(f''(c)=0\), то оцінити\(f'(x)\) в тестовій точці\(x\) зліва від\(c\) і контрольної точки\(x\) праворуч від\(c\), щоб визначити, чи\(f\) має локальний екстремум в\(c\).
Глосарій
- увігнуті вниз
- якщо\(f\) диференціюється протягом інтервалу\(I\) і\(f'\) зменшується над\(I\),\(f\) то увігнута вниз над\(I\)
- увігнуті вгору
- якщо\(f\) диференціюється протягом інтервалу\(I\) і\(f'\) збільшується більше\(I\),\(f\) то увігнуті вгору над\(I\)
- увігнутість
- вгору або вниз крива графіка функції
- тест на увігнутість
- \(f\)припустимо, двічі диференційовані протягом інтервалу\(I\); якщо\(f''>0\) над\(I\),\(f\) то увігнуті вгору над\(I\); якщо\(f''<\) над\(I\),\(f\) то увігнутий вниз над\(I\)
- перший похідний тест
- \(f\)нехай безперервна функція протягом інтервалу,\(I\) що містить критичну точку,\(c\) таку, яка\(f\) диференційована над\(I\) крім можливо в\(c\); якщо\(f'\) змінюється знак від позитивного до негативного, як\(x\) збільшується через\(c\), то \(f\)має локальний максимум при\(c\); якщо\(f'\) змінюється знак з негативного на позитивний як\(x\) збільшується через\(c\), то\(f\) має локальний мінімум при\(c\); якщо\(f'\) не змінює знак як\(x\) збільшується через\(c\), то\(f\) не має локального екстремуму при\(c\)
- точка перегину
- якщо\(f\) є безперервним в\(c\) і\(f\) змінюється увігнутість в\(c\), точка\((c,f(c))\) є точкою перегину\(f\)
- другий похідний тест
- припустимо,\(f'(c)=0\) і\(f'\) 'є безперервним протягом інтервалу\(f''(c)>0\), що містить\(c\); якщо, то\(f\) має локальний мінімум в\(c\); якщо\(f''(c)<0\), то\(f\) має локальний максимум в\(c\); якщо\(f''(c)=0\), то тест є непереконливим
