7.4: Довжина дуги та площа поверхні

Last updated
Save as PDF

Page ID: 60710

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Довжина дуги

У попередніх розділах ми використовували інтеграцію, щоб відповісти на наступні питання:

Враховуючи регіон, яка його площа?
З огляду на тверду речовину, який його обсяг?

У цьому розділі ми розглядаємо пов'язане питання: з огляду на криву, яка її довжина? Це часто називають довжиною дуги.

Розглянемо графік на$y=\sin x$$[0,\pi]$ наведеному на малюнку$\PageIndex{1a}$. Скільки триває ця крива? Тобто, якби ми використовували шматок рядка точно відповідати формі цієї кривої, як довго буде рядок?

Як ми робили в минулому, ми починаємо з наближення; пізніше ми уточнимо нашу відповідь, використовуючи обмеження, щоб отримати точне рішення.

Довжину прямолінійних відрізків легко обчислити за допомогою формули відстані. Ми можемо наблизити довжину заданої кривої, наблизивши криву прямими лініями і виміряючи їх довжини.

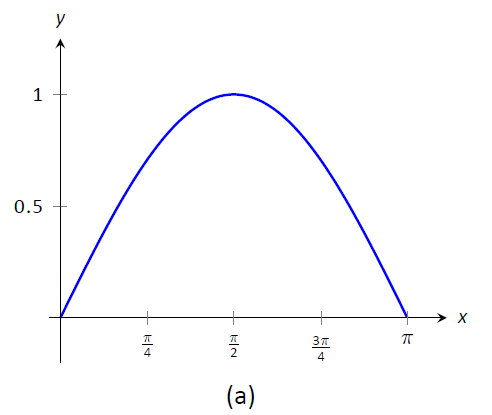
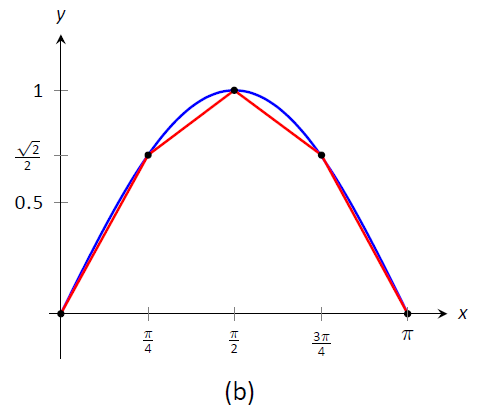
$7.4.1. PNG$ $7.4.1 б.пнг$

Малюнок$\PageIndex{1}$:$y=\sin x$ Графік$[0,\pi]$ і апроксимування кривої з відрізками лінії.

На малюнку$\PageIndex{1b}$ крива$y=\sin x$ була апроксимована з 4 відрізками лінії ($[0,\pi]$інтервал був розділений на 4 рівнодовгих підінтервалів). Зрозуміло, що ці чотири відрізки лінії наближаються$y=\sin x$ дуже добре на першому і останньому підінтервалі, хоча і не так добре посередині. Незалежно від того, сума довжин відрізків прямої є$3.79$, тому ми наближаємо довжину дуги$y=\sin x$$[0,\pi]$ на бути$3.79$.

Загалом, ми можемо наблизити довжину дуги$y=f(x)$$[a,b]$ на наступним чином. $a=x_1 < x_2 < \ldots < x_n< x_{n+1}=b$Дозволяти бути$[a,b]$ розділом на$n$ підінтервали. $dx_i$Дозволяти представляти довжину$i\,^\text{th}$ підінтервалу$[x_i,x_{i+1}]$.

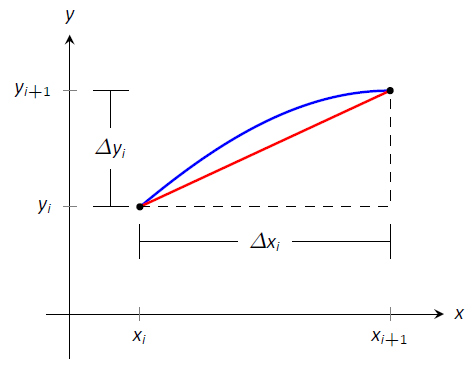
$7.4.2.png$

Рисунок$\PageIndex{2}$: Збільшення масштабу на$i\,^\text{th}$ підінтервалі$[x_i,x_{i+1}$] розділу$[a,b]$.

$\PageIndex{2}$Малюнок збільшується на$i\,^\text{th}$ підінтервалі, де$y=f(x)$ наближається прямим відрізком лінії. Пунктирні лінії показують, що ми можемо розглядати цей відрізок лінії, як вони гіпотенузи прямокутного трикутника, сторони якого мають довжину$dx_i$ і$dy_i$. Використовуючи теорему Піфагора, довжина цього відрізка лінії$\sqrt{dx_i^2 + \Delta y_i^2}.$ підсумовується по всіх підінтервалах дає наближення довжини дуги

\[L \approx \sum_{i=1}^n \sqrt{dx_i^2 + \Delta y_i^2}.\]

Як показано тут, це не сума Рімана. Хоча ми могли б зробити висновок, що беручи межу, оскільки довжина субінтервалу йде до нуля, дає точну довжину дуги, ми не зможемо обчислити відповідь з певним інтегралом. Нам потрібно спочатку зробити невелику алгебру.

У вищенаведеному факторі виразу$dx_i^2$ виводиться термін:

\[ \sum_{i=1}^n \sqrt{dx_i^2 + \Delta y_i^2} = \sum_{i=1}^n \sqrt{dx_i^2\left(1 + \frac{\Delta y_i^2}{dx_i^2}\right)}.\]

Тепер витягніть$dx_i^2$ термін з квадратного кореня:

\[= \sum_{i=1}^n\sqrt{1 + \frac{\Delta y_i^2}{dx_i^2}}\ dx_i.\]

Це майже сума Рімана. Розглянемо$\Delta y_i^2/dx_i^2$ термін. Вираз$\Delta y_i/dx_i$ вимірює «зміна$y$ в/зміна в»$x$, тобто «підйом над бігом»$f$ на$i\,^\text{th}$ підінтервалі. Теорема про середнє значення диференціювання (теорема 3.2.1) стверджує, що існує a$c_i$ в$i\,^\text{th}$ підінтервалі де$f'(c_i) = \Delta y_i/dx_i$. Таким чином, ми можемо переписати наш вищевказаний вираз як:

\[= \sum_{i=1}^n\sqrt{1+f'(c_i)^2}\ dx_i.\]

Це сума Рімана. Поки$f'$ є безперервним, ми можемо посилатися на теорему 5.3.2 і зробити висновок

\[= \int_a^b\sqrt{1+f'(x)^2}\ dx.\]

Ключова ідея 27: Довжина дуги

$f$Дозволяти диференціюватися на відкритому інтервалі$[a,b]$, що містить, де$f'$ також безперервно на$[a,b]$. Тоді довжина дуги$f$ від$x=a$ до$x=b$ дорівнює

\[L = \int_a^b \sqrt{1+f'(x)^2}\ dx.\]

Оскільки integrand містить квадратний корінь, часто важко використовувати формулу в Key Idea 27, щоб точно знайти довжину. Коли точні відповіді важко знайти, ми вдаємося до використання числових методів наближення певних інтегралів. Наведені нижче приклади продемонструють це.

Приклад$\PageIndex{1}$: Finding arc length

Знайти довжину дуги$f(x) = x^{3/2}$ від$x=0$ до$x=4$.

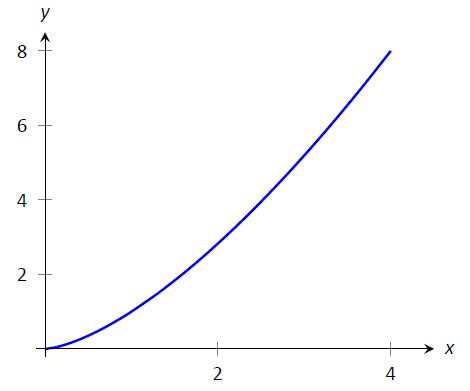
$7.4.3.png$

Малюнок$\PageIndex{3}$: Графік$f(x) = x^{3/2}$ з Прикладу$\PageIndex{1}$

Рішення

Починаємо з пошуку$f'(x)= \frac32x^{1/2}$. Використовуючи формулу, знаходимо довжину дуги$L$ як

\[\begin{align} L &= \int_0^4 \sqrt{1+\left(\frac32x^{1/2}\right)^2}\ dx \\ &= \int_0^4 \sqrt{1+\frac94x} \ dx \\ &= \int_0^4 \left(1+\frac94x\right)^{1/2}\ dx \\ &= \frac23\frac49\left(1+\frac94x\right)^{3/2}\Big|_0^4 \\ &=\frac{8}{27}\left(10^{3/2}-1\right) \approx 9.07 \text{units}.\end{align}\]

Приклад$\PageIndex{2}$: Finding arc length

Знайти довжину дуги$f(x) =\frac18x^2-\ln x$ від$x=1$ до$x=2$.

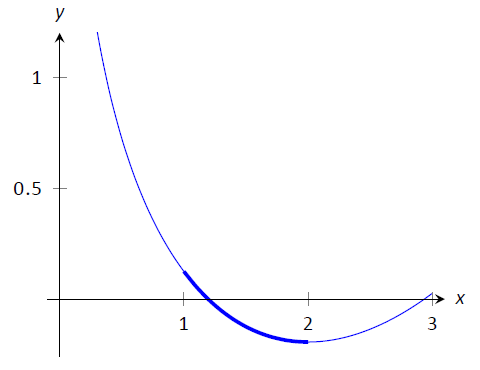
$7.4.4.png$

Малюнок$\PageIndex{4}$: Графік$f(x) =\frac18x^2-\ln x$ з Прикладу$\PageIndex{2}$.

Рішення

Ця функція була обрана спеціально тому, що отриманий інтеграл можна точно оцінити. Починаємо з пошуку$f'(x) = x/4-1/x$. Довжина дуги дорівнює

\[\begin{align} L&= \int_1^2 \sqrt{1+ \left(\frac x4-\frac1x\right)^2}\ dx \\ &= \int_1^2 \sqrt{1 + \frac{x^2}{16} -\frac12 + \frac1{x^2} } \ dx \\ &= \int_1^2 \sqrt{\frac{x^2}{16} +\frac12 + \frac1{x^2} } \ dx \\ &= \int_1^2 \sqrt{ \left(\frac x4 + \frac1x\right)^2}\ dx &= \int_1^2 \left(\frac x4 + \frac1x\right) \ dx \\ &= \left(\frac{x^2}8 + \ln x\right)\Bigg|_1^2\\ &= \frac38+\ln 2 \approx 1.07 \ \text{units}.\end{align}\]

Графік$f$ наведено на малюнку$\PageIndex{4}$; частина кривої, виміряна в цій задачі, виділена жирним шрифтом.

Попередні приклади знайшли довжину дуги саме завдяки ретельному вибору функцій. Взагалі точні відповіді набагато складніше знайти і необхідні числові наближення.

Приклад$\PageIndex{3}$: Approximating arc length numerically

Знайти довжину синусоїдальної кривої від$x=0$ до$x=\pi$.

Рішення

Це дещо математична цікавість; у прикладі 5.4.3 ми виявили, що площа під одним «горбом» кривої синуса становить 2 квадратні одиниці; тепер ми вимірюємо довжину її дуги.

Налаштування проста:$f(x) = \sin x$ і$f'(x) = \cos x$. Таким чином

\[L = \int_0^\pi \sqrt{1+\cos^2x}\ dx.\]

Цей інтеграл не може бути оцінений з точки зору елементарних функцій, тому ми наблизимо його методом Сімпсона с$n=4$.

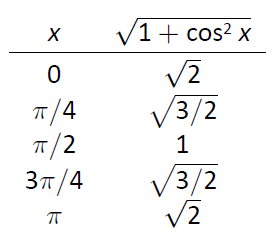
$7.4.5.png$

Рисунок$\PageIndex{5}$: Таблиця значень$y=\sqrt{1+\cos^2x}$ для оцінки певного інтеграла в прикладі$\PageIndex{3}$.

\[\begin{array}{cc}x & \sqrt{1+\cos^2x} \\ \hline 0 & \sqrt{2}\\ \pi/4 & \sqrt{3/2} \\ \pi/2 & 1 \\ 3 \pi/4 & \sqrt{3/2} \\ \pi & \sqrt{2} \\\end{array}\]

Рисунок\ ref {fig:arc3} дає$\sqrt{1+\cos^2x}$ оцінку в 5 рівномірно розташованих точках в$[0,\pi]$. Правило Сімпсона тоді стверджує, що

\[\begin{align} \int_0^\pi \sqrt{1+\cos^2x}\ dx &\approx \frac{\pi-0}{4\cdot 3}\left(\sqrt{2}+4\sqrt{3/2}+2(1)+4\sqrt{3/2}+\sqrt{2}\right) \\ &=3.82918.\end{align}\]

Використання комп'ютера з$n=100$ наближенням є$L\approx 3.8202$; наше наближення з$n=4$ є досить хорошим.

Площа поверхні твердих тіл обертання

Ми вже бачили, як крива$y=f(x)$ на$[a,b]$ може обертатися навколо осі, утворюючи тверде тіло. Замість того, щоб обчислювати його обсяг, ми тепер розглянемо його площу поверхні.

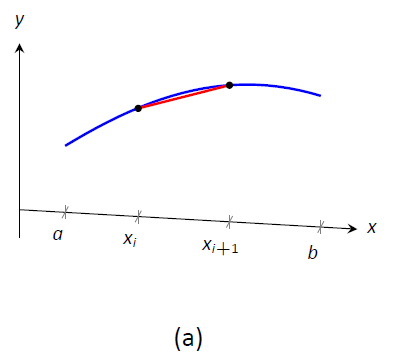
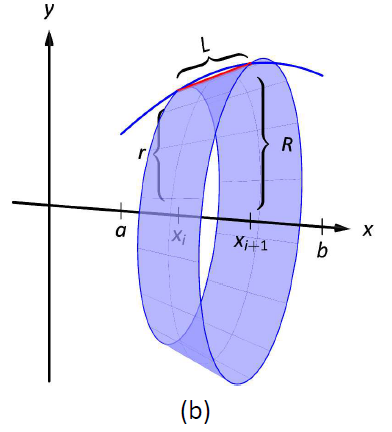
$7.4.6a.png$ $7.4.6 б.пнг$

Малюнок$\PageIndex{6}$: Встановлення формули для площі поверхні.

Починаємо так, як у нас є в попередніх розділах: поділяємо інтервал$[a,b]$ з$n$ підінтервалами, де знаходиться$i\,^{\text{th}}$ підінтервал$[x_i,x_{i+1}]$. На кожному підінтервалі ми можемо наблизити$y=f(x)$ криву прямою лінією, яка з'єднує$f(x_i)$ і$f(x_{i+1})$ як показано на малюнку$\PageIndex{5a}$. Обертання цього відрізка лінії навколо$x$ -осі створює частину конуса (називається frustum конуса), як показано на малюнку$\PageIndex{5b}$. Площа поверхні плоду конуса становить

\[2\pi\cdot\text{ length }\cdot\text{average of the two radii $R$ and $r$}.\]

Довжина задається$L$; ми використовуємо матеріал, щойно покритий довжиною дуги, щоб заявити, що

\[L\approx \sqrt{1+f'(c_i)}dx_i\]

для деяких$c_i$ в$i\,^\text{th}$ субінтервалі. Радіуси - це лише функція, що оцінюється в кінцевих точках інтервалу. Тобто,

\[R = f(x_{i+1})\quad \text{and}\quad r = f(x_i).\]

Таким чином, площа поверхні цього зразка плоду конуса приблизно дорівнює.

\[2\pi\frac{f(x_i)+f(x_{i+1})}2\sqrt{1+f'(c_i)^2}dx_i.\]

Оскільки$f$ є безперервною функцією, Теорема проміжних значень стверджує, що є деякі$d_i$$[x_i,x_{i+1}]$ такі, що$f(d_i) = \frac{f(x_i)+f(x_{i+1})}2$; ми можемо використовувати це, щоб переписати вищевказане рівняння як

\[2\pi f(d_i)\sqrt{1+f'(c_i)^2}dx_i.\]

Підсумовуючи по всіх субінтервалах, отримуємо загальну площу поверхні приблизно.

\[\text{Surface Area}\approx \sum_{i=1}^n 2\pi f(d_i)\sqrt{1+f'(c_i)^2}dx_i,\]

яка є Сумою Рімана. Беручи межу, оскільки довжини підінтервалу йдуть до нуля, дає нам точну площу поверхні, наведену в наступній ключовій ідеї.

Ключова ідея 28: Площа поверхні твердого тіла революції

$f$Дозволяти диференціюватися на відкритому інтервалі$[a,b]$,$f'$ що містить де також безперервно на$[a,b]$.

Площа поверхні твердого тіла, утвореного при обертанні графіка$y=f(x)$, де$f(x)\geq0$, близько$x$ -осі знаходиться

$\ текст {Площа поверхні} = 2\ pi\ int_a^b f (x)\ sqrt {1+f' (x) ^2}\ dx.\]

Площа поверхні твердого тіла, утворена при обертанні графіка$y=f(x)$ приблизно$y$ -осі$a,b\geq0$, де,

$\ текст {Площа поверхні} = 2\ pi\ int_a^b x\ sqrt {1+f' (x) ^2}\ dx.\]

При обертанні$y=f(x)$ навколо$y$ -осі радіуси отриманого frustum є$x_i$ і$x_{i+1}$; їх середнє значення просто середина інтервалу. У межі, ця середина справедлива$x$. Це дає другу частину Key Idea 28.

Приклад$\PageIndex{4}$: Finding surface area of a solid of revolution

Знайдіть площу поверхні твердого тіла, утвореного$y=\sin x$ обертанням$[0,\pi]$ навколо$x$ -осі, як показано на малюнку$\PageIndex{6}$.

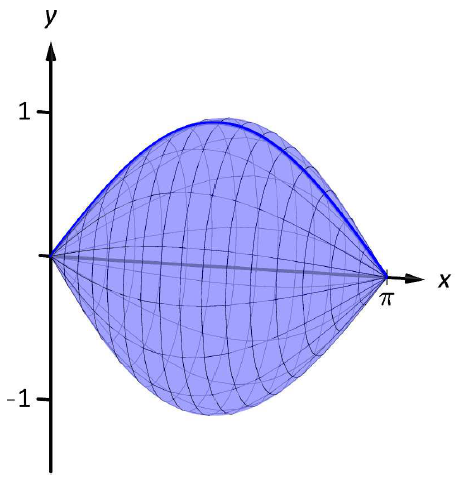
$7.4.7.png$

Малюнок$\PageIndex{7}$:$y=\sin x$ Обертається$[0,\pi]$ навколо$x$ -осі.

Рішення

Налаштування відносно проста. Використовуючи Key Idea\ ref {idea:surface_area}, ми маємо площу$SA$ поверхні:

\[\begin{align}SA &= 2\pi\int_0^\pi \sin x\sqrt{1+\cos^2x}\ dx \\ &= -2\pi\frac12\left.\left(\sinh^{-1}(\cos x)+\cos x\sqrt{1+\cos^2x}\right)\right|_0^\pi \\ &= 2\pi\left(\sqrt{2}+\sinh^{-1} 1\right) \\ &\approx 14.42\ \text{units}^2.\end{align}\]

Крок інтеграції вище нетривіальний, використовуючи метод інтеграції під назвою тригонометрична заміщення.

Цікаво бачити, що площа поверхні твердого тіла, форма якого визначається тригонометричною функцією, включає як квадратний корінь, так і обернену гіперболічну тригонометричну функцію.

Приклад$\PageIndex{5}$: Finding surface area of a solid of revolution

Знайдіть площу поверхні твердого тіла, утвореного обертанням кривої$y=x^2$ на$[0,1]$ приблизно:

$x$-вісь
$y$-вісь.

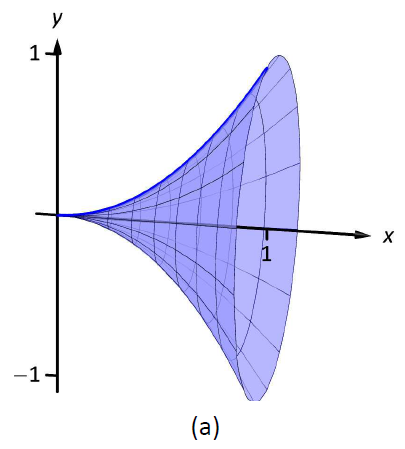
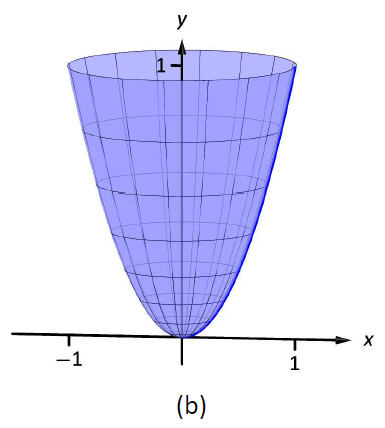
$7.4.8a.png$ $7.4.8 б.пнг$

Малюнок$\PageIndex{8}$: Тверді речовини, використовувані в прикладі$\PageIndex{6}$.

Рішення

Інтеграл простий в налаштуванні:

\[SA = 2\pi\int_0^1 x^2\sqrt{1+(2x)^2} dx.\]

Як і інтеграл у прикладі\ ref {ex_sa1}, для цього потрібна тригонометрична заміна.

\[\begin{align} &= \left.\frac{\pi}{32}\left(2(8x^3+x)\sqrt{1+4x^2}-\sinh^{-1}(2x)\right)\right|_0^1\\ &=\frac{\pi}{32}\left(18\sqrt{5}-\sinh^{-1}2\right)\\ &\approx 3.81\ \text{units}^2. \end{align}\]

Тверде тіло, утворене$y=x^2$ обертанням навколо$x$ -осі, зображено на малюнку$\PageIndex{7a}$.

Оскільки ми обертаємося навколо$y$ -осі, «радіус» твердого тіла не є,$f(x)$ а скоріше$x$. Таким чином, інтегралом для обчислення площі поверхні є:

\[SA = 2\pi\int_0^1x\sqrt{1+(2x)^2} dx.\]

Цей інтеграл можна вирішити за допомогою підстановки. Встановити$u=1+4x^2$; нові межі мають$u=1$ бути$u=5$. У нас тоді є
\[\begin{align} &= \frac{\pi}{4}\int_1^5 \sqrt{u} du \\ &= \frac{\pi}{4}\frac{2}{3} u^{3/2}\big|_1^5 \\ &= \frac{\pi}{6}\left ( 5\sqrt{5}-1\right ) \\ &\approx 5.33 \text{ units}^2. \end{align}\]

Тверде тіло, утворене$y=x^2$ обертанням навколо$y$ -осі, зображено на малюнку$\PageIndex{7b}$.

Наш останній приклад - відомий математичний «парадокс».

Приклад$\PageIndex{6}$: The surface area and volume of Gabriel's Horn

Розглянемо тверде тіло, утворене$y=1/x$ обертанням навколо$x$ -осі на$[1,\infty)$. Знайдіть обсяг і площу поверхні цього твердого тіла. (Ця форма, як показано на малюнку$\PageIndex{9}$, відома як «Ріг Гавриїла», оскільки вона виглядає як дуже довгий ріг, який може грати лише надприродна людина, наприклад ангел.)

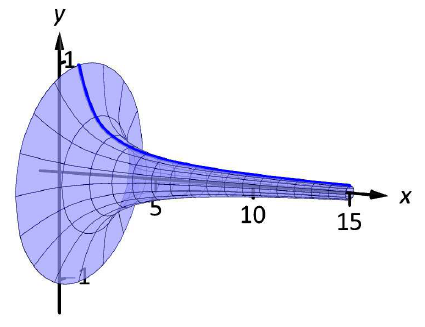
$7.4.9.png$

Малюнок$\PageIndex{9}$: Графік рогу Гавриїла.

Рішення

Для обчислення томи природно використовувати метод диска. У нас є:

\[\begin{align}V &= \pi\int_1^\infty \frac{1}{x^2}\ dx \\ &= \lim_{b\to\infty}\pi\int_1^b\frac{1}{x^2}\ dx \\ &= \lim_{b\to\infty} \left.\pi\left(\frac{-1}{x}\right)\right|_1^b \\ &= \lim_{b\to\infty} \pi\left(1-\frac1b\right) \\ &= \pi \ \text{units}^3.\end{align}\]

Горн Гавриїла має кінцевий об'єм$\pi$ кубічних одиниць. Оскільки ми вже бачили, що регіони з нескінченною довжиною можуть мати кінцеву площу, це не надто важко прийняти.

Розглянемо тепер його площу поверхні. Інтеграл простий в налаштуванні:

\[SA = 2\pi\int_1^\infty \frac{1}{x}\sqrt{1+1/x^4}\ dx.\]

Інтегрувати цей вираз не тривіально. Однак ми можемо порівняти його з іншими невідповідними інтегралами. З тих пір$1< \sqrt{1+1/x^4} $$[1,\infty)$, ми можемо констатувати, що

\[2\pi\int_1^\infty \frac{1}{x} dx <2\pi\int_1^\infty \frac{1}{x}\sqrt{1+1/x^4} dx .\]

За Key Idea 21 неправильний інтеграл зліва розходиться. Оскільки інтеграл праворуч більший, ми робимо висновок, що він також розходиться, тобто Ріг Гавриїла має нескінченну площу поверхні.

Звідси «парадокс»: ми можемо заповнити Ріг Габріеля кінцевою кількістю фарби, але оскільки вона має нескінченну площу поверхні, ми ніколи не зможемо її пофарбувати.

Якось цей парадокс вражає, коли ми думаємо про це з точки зору обсягу та площі. Однак ми бачили подібний парадокс і раніше, про що йшлося вище. Ми знаємо, що площа під кривою$y=1/x^2$ на$[1,\infty)$ кінцева, але форма має нескінченний периметр. Дивні речі можуть статися, коли ми маємо справу з нескінченним.

Стандартне рівняння з фізики - «Робота = сила$\times$ відстані», коли прикладена сила постійна. У наступному розділі ми дізнаємося, як обчислити роботу, коли прикладена сила є змінною.